光栅投影三维测量解相位方法的对比研究

徐昆鹏，王建华

（1.徐州工业职业技术学院 机电工程学院，江苏徐州，221140；2.青岛理工大学 自动化工程学院，山东青岛，266520）

0 引言

基于光栅投影的光学三维面形测量具有非接触、精度高、速度快、低成本、全场测量和易于实现等特点，在逆向工程、工业检测、质量控制、虚拟现实、医学诊断、文物修复和物体识别等领域应用广泛[1]。相移轮廓术(PSM)和傅里叶变换轮廓术(FTP)是两种传统方法。相移法[2]计算简单，测量精度高，但对噪声比较敏感，噪声会引起解相位结果存在大量虚假2π跳变，增加了相位展开的难度，且至少需要三幅以上的条纹图像，适用于静态测量；傅里叶变换法[3]是M.Takeda等人在1983年提出来的，它只需要一幅条纹图案，即可恢复物体三维形貌，可用于动态物体的三维形貌测量；但由于傅里叶变换不具有局部分析的能力，频谱混叠等问题，影响了其测量精度。小波变换具有多分辨率分析特点，抑噪能力强，可分为一维小波变换轮廓术(1D WTP)和二维小波变换轮廓术(2D WTP)[4-6]。小波脊提取是小波变换轮廓术的关键步骤，最大模法是常见的小波脊提取方法。

本文分析了相移法、傅里叶变换法和一维、二维小波变换法解相位的原理，对比了几种方法的解相位结果。针对条纹图存在较强噪声干扰，小波变换最大模提取算法会产生较大误差，提出了基于价值函数的二维小波变换小波脊提取算法。首先，提取二维小波变换系数模的最大值点和部分局部极值点，共同作为小波脊候选点；其次，根据噪声产生的较大系数模可以使用小波脊连续性进行去除这一原理，在二维小波变换系数的模上引入尺度因子的梯度，建立价值函数，评估所有候选点的价值；最后，确定每行条纹的最优小波脊。仿真和实验证明，该方法的抑噪能力明显优于其他几种解相位方法。

1 原理

1.1 相移轮廓术

相移法[7]的投影条纹一般为余弦条纹（或正弦），得到条纹的灰度值用下式（1）表示：

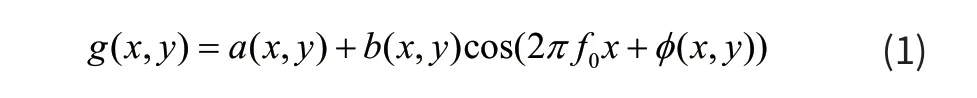
式中，a(x,y)为背景光强值，b(x,y)为调制强度，f0为载波频率，φ(x,y)为被测物体高度调制相位。

沿着垂直于光栅条纹方向在一个周期内移动n次，n∈ (3,5)。当n= 3时称为三步相移法，当n= 4时称为四步相移法，当n= 5时称为五步相移法。以四步相移法为例，四幅带有 /2π相移的灰度值函数分别用下式（2）～（5）表示：

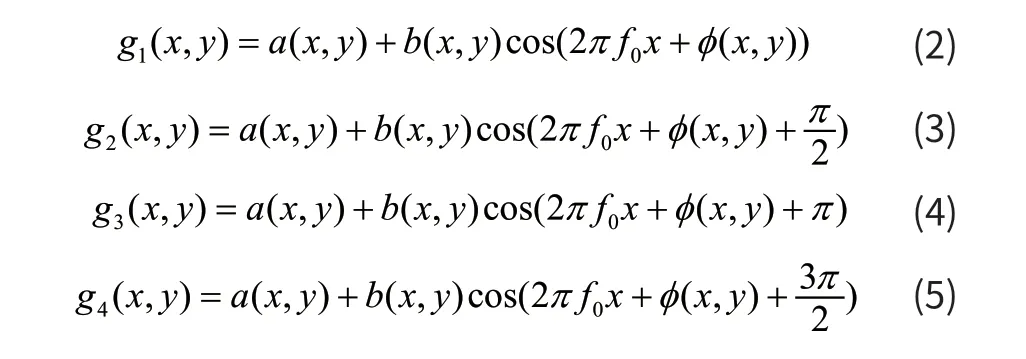
得到：

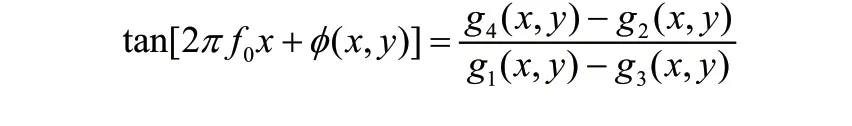
求取反正切函数，得到：

式（6）反正切运算得到的相位值 (,)xyψ包裹在(-,]ππ之间，称为相位主值（或包裹相位），需要相位展开得到实际相位。

1.2 傅里叶变换轮廓术

傅里叶变换解相位的基本原理是在频域中把代表背景光的零频分量和代表噪声的高频分量通过合适的滤波器滤除掉，剩下的是包含有用相位信息的基频分量，再对基频分量进行逆傅里叶变换，通过正切运算即可解出被测物体高度调制相位主值。

根据欧拉公式，式（1）可以（7）表示为：

式中：

沿x方向对式（2）采用一维傅里叶变换，得到：

上式（8）由-1级C*(f+f0)、0级A(f)、1级C(f-f0)三种频谱信号组成，如图1所示。

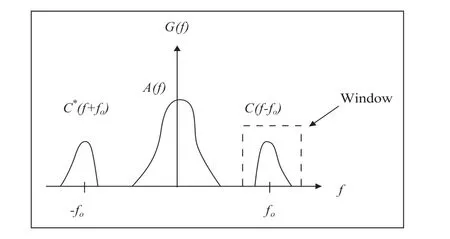
图1 一维傅里叶变换的基频分量提取

其中A(f)其代表零频背景信号，而C(f-f0)、C*(f+f0)包含了所需的相位信号。这里选取 0(-)Cff，逆傅里叶变换得到：

其实部和虚部分别为：

被测物体高度调制相位主值可以写成：

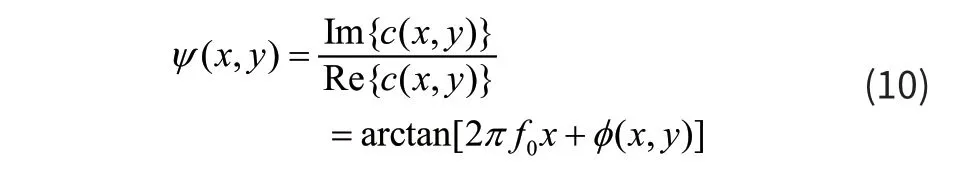
同相移法类似，傅里叶变换法得到的相位主值也是截断的，即包裹在(-,]ππ之间，需要相位展开得到实际相位。

1.3 小波变换轮廓术

1.3.1 一维小波变换法

图2(a)为模拟被测物体1Peaks× ，图像大小为512pixels×512pixels，被测物体高度调制后的变形条纹如图2(b)所示，选取变形条纹第256行像素的灰度值组成一维数组g(256,:)(x)。

图2 被测物体和变形条纹

对一维数组g(256,:)(x)一维小波变换：

式中： (,)Wbs为一维小波变换系数，b为平移因子，s为伸缩因子（或称尺度因子），母小波 ()xψ选择一维Morlet小波，表达式为：

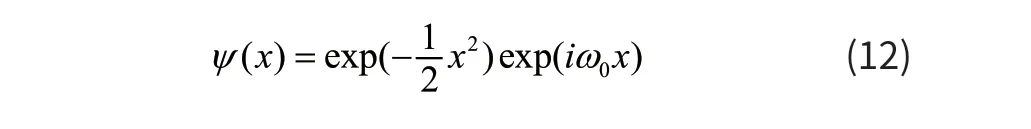
一维小波变换系数是二维的，其模和相位分布分别用公式（13）、（14）表示：

式中：Modulus是一维小波变换系数的模，如图3(a)所示，横轴为平移因子b，取值范围为1～512pixles，竖轴为系数模，白色表示系数模比较大，黑色表示系数模比较小；phase_map是一维小波变换系数的相位，如图3(b)所示，横轴为尺度因子s，取值范围为1～64，竖轴为相位。

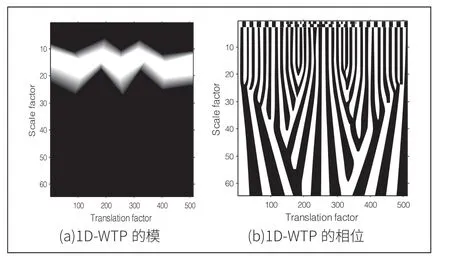
图3 变形条纹的一维小波变换

小波变换系数模的最大值定义为小波变换的“脊”，“脊线”则代表了信号和Morlet小波最为相似的位置，提取出“脊线”位置处对应的相位，即为第256行像素的相位主值，条纹所有行像素采用同样方式得到相位主值，从而获得整幅条纹图案的相位主值分布[8-11]。

1.3.2 二维小波变换法

二维小波变换不但含有平移因子和尺度因子，而且含有旋转因子，因此具有方向选择性，其多分辨率分析能力强于一维小波变换。其原理是把小波不断平移、缩放和旋转，与原始信号进行比较，计算得到小波变换系数矩阵。系数模代表小波与信号的相似程度，系数模值越高，表示小波与信号越相似。通过寻找二维小波系数的最大模，来恢复相位主值[12]。

在二维小波变换中，母小波采用二维Morlet复小波[13-14]，表示为：

式中：θ为小波相对于x旋转角度，k为小波中心频率。

变形条纹 (,)gxy二维小波变换表达式为：

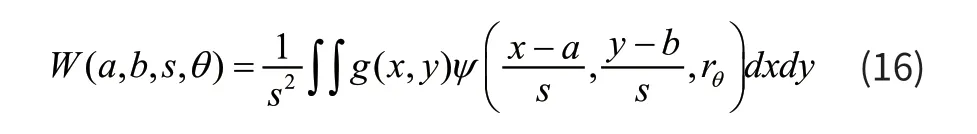
式中：W(a,b,s,θ)为小波变换系数，(a,b)为两个方向上的平移因子，s为伸缩因子（或称尺度因子），θ为旋转角度，rθ为旋转矩阵。

如果尺度因子s有六十四种不同的取值，旋转角度因子s有四种不同的取值，那么将整幅变形条纹二维小波变换后得到一个四维数据为512×512×64×4，取出每个512×512矩阵第一个位置点的数值，组成64×4系数矩阵，它是第1行、第1列像素点在不同缩放尺度和旋转角度下的二维小波变换系数矩阵，如图4所示。

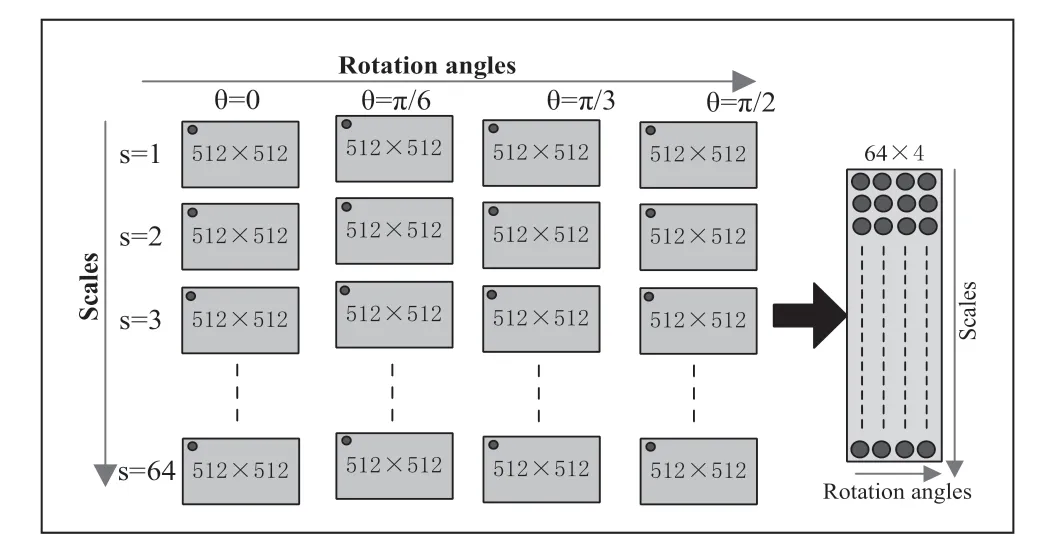
图4 二维小波变换的四维数据

根据式（13）、（14）求出该像素点的模和相位，找到系数模最大值，进一步得到最大值点的相位值，即为该像素点的相位主值。依次提取出512×512矩阵其他像素点的数据，提取最大系数模位置相对应的相位，从而得到整幅条纹的相位主值。

1.4 几种方法的仿真对比

计算机生成模拟被测物体为0.5Peaks，条纹周期为16Pixels，相位展开采用Itoh提出的基本相位展开方法[15-16]（逐行相位展开方法），以均方根误差（RMSE）作为评价标准，对比各种方法的面形恢复、误差如表1所示。通过对比几种方法的解相位结果可以看出，相移法测量精度最高，误差最小。

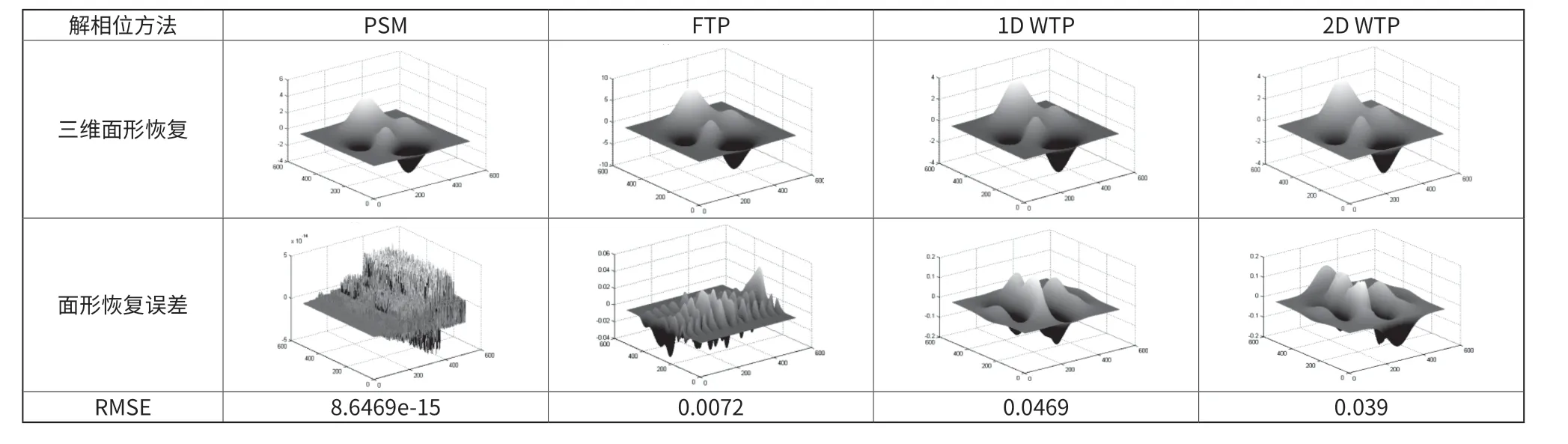
表1 理想无噪声干扰条纹图，不同方法的三维面形恢复和误差

2 基于评价函数二维小波变换脊提取算法

小波变换直接最大模小波脊提取方法的特点是算法简单，速度快。但是，当条纹图像中存在噪声时，会出现多个局部极大值点，小波变换系数模不是最大值点，也是局部极大值点。如果仍然采用模最大值搜索“脊”，将找到错误的“脊”，而导致恢复的三维形貌存在较大误差。通过前面的分析可以看出，系数模的“脊”一般是连续的，而噪声产生的局部极值点可以选用系数模“脊线”的连续性进行去除。根据以上特性，提出了基于评价函数的二维小波脊提取算法。

2.1 评价函数

评价函数定义为：

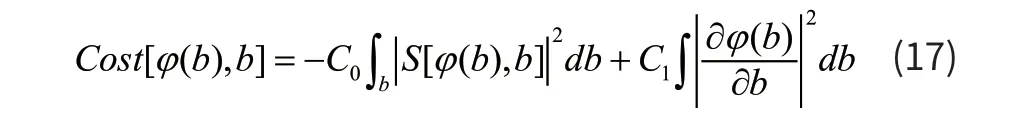
式中：φ(b)为尺度因子，b为平移因子，S[φ(b),b]为小波变换系数((),)bbφ位置的模，代表了尺度因子的梯度，C0和C1为权值。

根据前面分析，系数模越大且路径越光滑，则越能代表实际“脊线”。由式（17）可以看出，S[φ(b),b]越大，越小，价值函数值也越小，越能反映真实的“小波脊线”。

假设C0和C1取值为1，价值函数最小的路径经过点(p,j)，其中尺度因子p=φ(j)，j为平移因子，则后面一点(q,j+ 1)的价值函数可表示为：

2.2 算法步骤

Step1: 对条纹图进行二维小波变换，得到一个四维的系数矩阵。

Step2: 0θ= 时，取出尺度因子为1,2……64时每个矩阵的第一行系数，组成64512× 系数矩阵，它代表了 0θ= 时、第一行像素的系数矩阵。采用相同的方法，取出其他三个旋转角度中每个矩阵的第一行系数，组成各自的第一行像素系数矩阵，如图5所示。

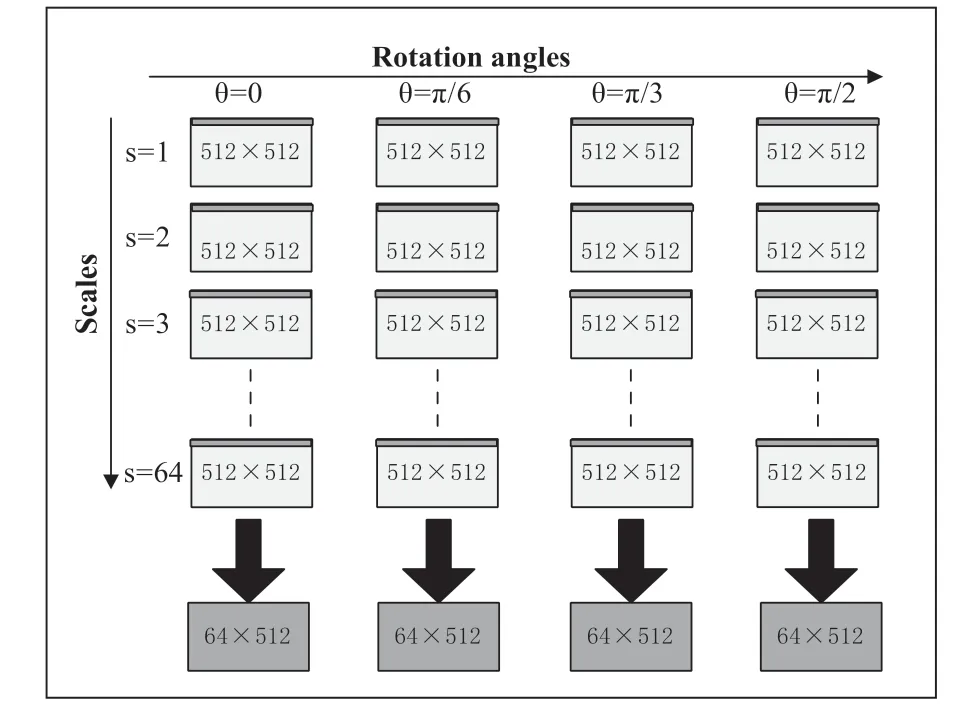
图5 基于价值函数的二维小波变换四维系数矩阵

Step3: 取θ= 0时，第一行像素的64 × 512系数矩阵的模和如图6所示。在图6中依次找出平移因子为b= 1,b= 2， ······b=512时，模的最大值和最大值90%的局部极值点，共同组成候选脊点，图7为候选脊点的模，而候选脊点所对应尺度因子如图8所示。由于噪声的影响，所有候选点都有可能是最终的“脊”。因此，根据式（18）计算所有候选点的价值；第一列的价值都为0，第2列价值的计算过程如图9所示。

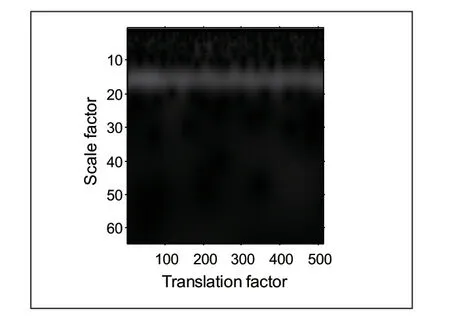
图6 二维小波变换系数矩阵 0θ= 第一行像素的模

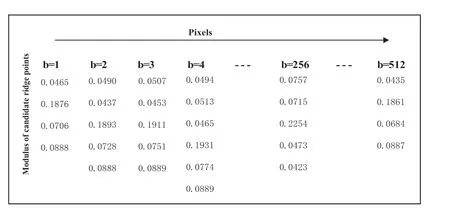
图7 候选脊点的模

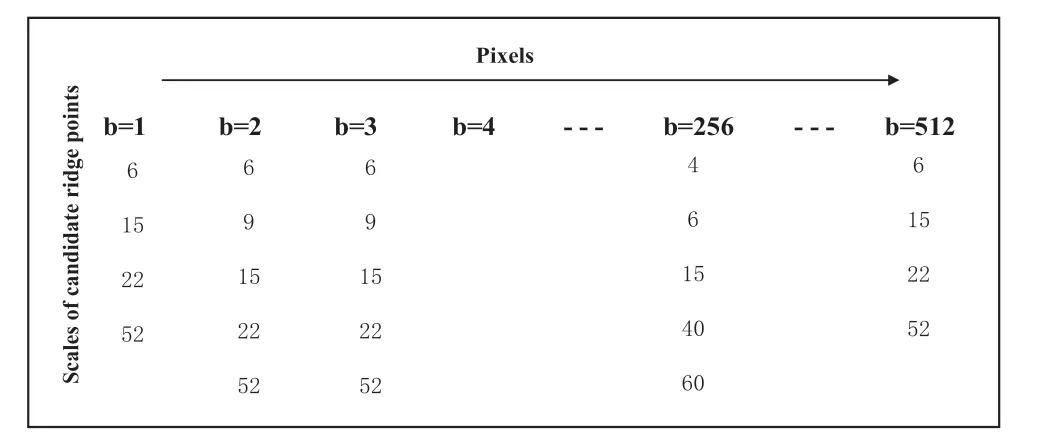
图8 候选脊点的尺度因子

图9 候选脊点的价值计算

Step4: 找到第512列像素点的所有候选点的最小价值，并记录该候选点的位置（即尺度因子和系数模），然后找出该最小价值的求解路径，从而确定第511像素点的小波脊位置，然后按照上述方法反向寻找到所有最优路径，即可找到第512～1列位置，即为 0θ= 时第一行像素的最优小波脊线，如图10所示。

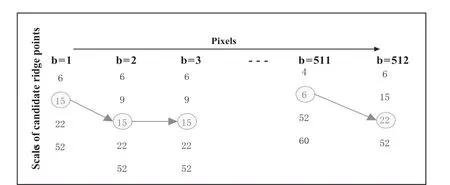
图10 最优小波脊线

3 计算机模拟和实验

3.1 计算机模拟

采用计算机模拟验证所提方法的抑噪性能。模拟被测物体为0.5×Peaks，条纹图大小为512pixle×512pixel，采用均方根误差（RMSE）衡量形貌恢复精度。依次加入标准方差梯度0.1递增的高斯白噪声和椒盐噪声，对比二维小波变换的直接最大模的小波脊提取和基于价值函数的小波脊提取，如图11和12所示。信噪比较低时，基于价值函数的小波脊提取算法的均方根误差明显小于直接最大模的小波脊提取方法。

图11 不同椒盐噪声等级时的RMSE

图12 不同高斯白噪声等级时的RMSE

3.2 实验

测量系统主要由数字投影仪（三星SP-P410M）、CCD相机（大恒水星系列MER-050-560U3M）和个人计算机（Intel Core i5-4258U CPU, 4G RAM）组成，如图13所示。

图13 测量系统

被测物体为三维凸起曲面，条纹图存在噪声污染，采集到的条纹图如图14(a)所示，分别采用二维小波变换最大模的小波脊提取和基于价值函数的小波脊提取算法获得包裹相位，然后用Itoh逐行逐列相位展开方法得到实际相位分布，结果如图14(b)和(c)所示。通过对比可以看出，相对于最大模提取算法，基于价值函数的二维小波脊提取形貌恢复精度更高，结果更好。

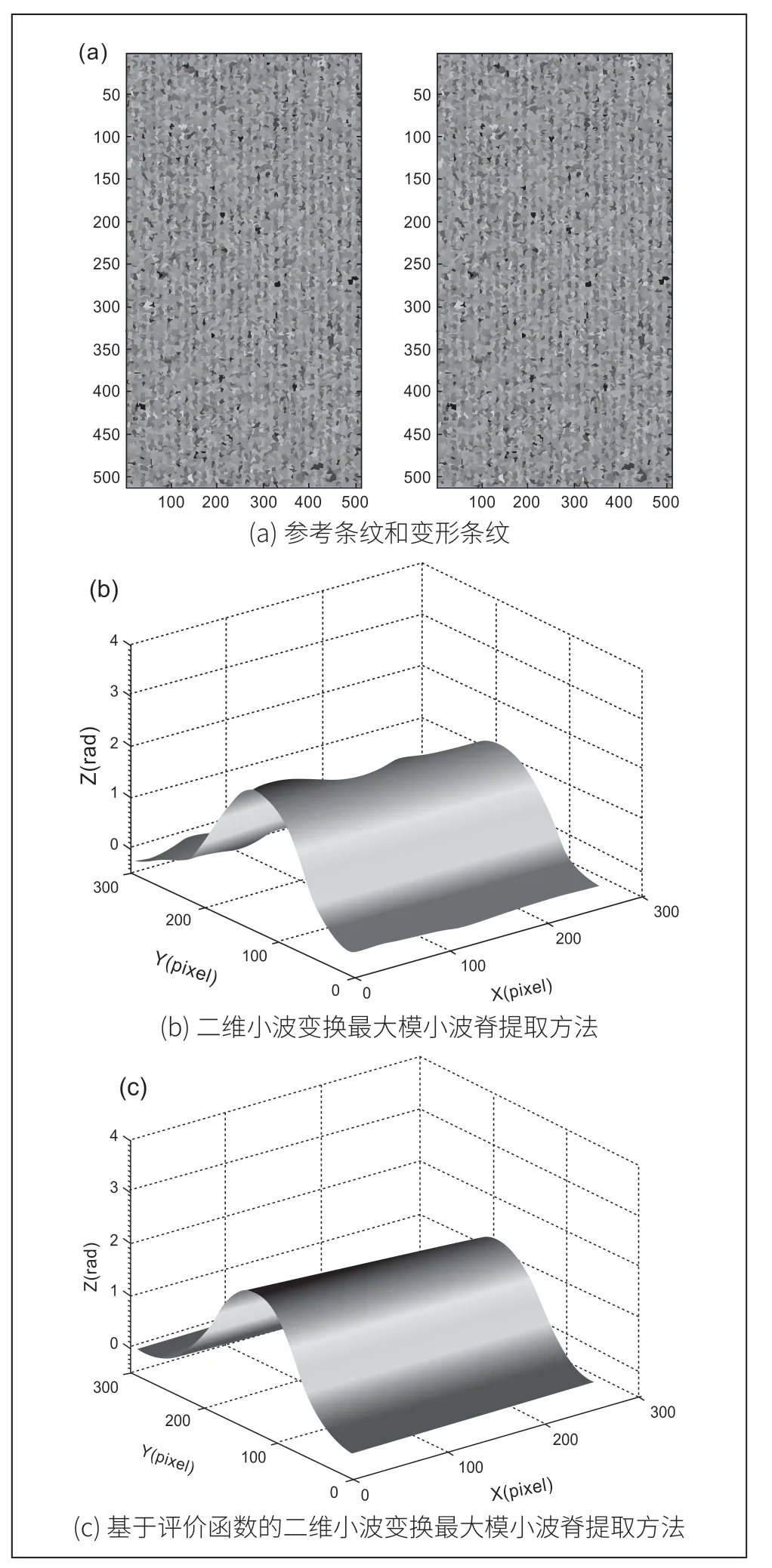
图14 曲面实验对比

4 结论

光栅条纹投影轮廓术的解相位方法主要有相移法、傅里叶变换法和小波变换法。本文分析了几种方法的原理，并对测量精度进行了对比分析，研究发现相移法解相位精度最高，但所需条纹数量较多，适合静态物体测量；傅里叶变换和小波变换只需一幅条纹即可获得相位主值，但测量精度低于相移法。此外，当条纹图存在较强噪声干扰，小波变换最大模提取算法会产生较大误差，提出了一种基于价值函数的二维小波变换小波脊提取算法，相对于二维小波变换直接最大脊提取算法，抑噪能力更好。