Maneuvering Angle Rigid Formations With Global Convergence Guarantees
2022-08-13LiangmingChenZhiyunLinHectorGarciadeMarinaZhiyongSunandMirFeroskhan
Liangming Chen, Zhiyun Lin,, Hector Garcia de Marina,,Zhiyong Sun, and Mir Feroskhan
Abstract—Angle rigid multi-agent formations can simultaneously undergo translational, rotational, and scaling maneuvering,therefore combining the maneuvering capabilities of both distance and bearing rigid formations. However, maneuvering angle rigid formations in 2D or 3D with global convergence guarantees is shown to be a challenging problem in the existing literature even when relative position measurements are available. Motivated by angle-induced linear equations in 2D triangles and 3D tetrahedra,this paper aims to solve this challenging problem in both 2D and 3D under a leader-follower framework. For the 2D case where the leaders have constant velocities, by using local relative position and velocity measurements, a formation maneuvering law is designed for the followers governed by double-integrator dynamics. When the leaders have time-varying velocities, a sliding mode formation maneuvering law is proposed by using the same measurements. For the 3D case, to establish an angle-induced linear equation for each tetrahedron, we assume that all the followers’ coordinate frames share a common Z direction. Then,a formation maneuvering law is proposed for the followers to globally maneuver Z-weakly angle rigid formations in 3D. The extension to Lagrangian agent dynamics and the construction of the desired rigid formations by using the minimum number of angle constraints are also discussed. Simulation examples are provided to validate the effectiveness of the proposed algorithms.
I. INTRODUCTION
MULTI-AGENT formations have been extensively studied [1] to enable numerous impactful applications,such as target search and rescue [2], unknown environment exploration [3], and cooperative surveillance [4]. In most of these practical applications, the agents are required to have the capability of not only achieving a specific formation shape,but also maneuvering collectively as a whole in translation,rotation, scaling, and with even more complicated motion forms [5]–[12].
To achieve the aforementioned formation maneuvering task,various control approaches have been proposed, which can be categorized into different types according to the constraints used to specify the desired formation shape [7], [13], [14]. For relative position-constrained formations [15]–[17], since the inter-agent relative positions are invariant when the associated agents translate with the same magnitude, translational formation maneuvering can be achieved, assuming that the agents’coordinate frames are aligned. Since inter-agent distances are invariant under the agents’ translation and rotation, both translational and rotational formation maneuvering are achieved for distance rigid formations [18]. Also, since interagent bearings are invariant under the agents’ translational and scaling motions [13], both translational and scaling formation maneuvering are achieved for bearing rigid formations [13],[19], [20], where the results hold for an arbitrary dimensional space provided that the agents’ coordinate frames are aligned.Under a leader-follower framework, the bearing-constrained formation tracking problem has been investigated in [21],[22], where the translational formation maneuvering is achieved by using relative position and absolute velocity measurements. Unlike the distance and bearing rigid formations alone,angle rigid formations can undergo simultaneously translational, rotational and scaling maneuvering because any angle constraints are invariant under these three types of formation maneuvering motions [7], [23], [24]. With the advantage of having more formation maneuvering freedoms, angle rigid formation maneuvering algorithms have been designed in [7]for single-integrator agents, and in [25] for double-integrator agents. However, their convergence to their respective desired formations under the designed formation maneuvering algorithms [7], [25] is only locally guaranteed. Due to the high nonlinearity in the angle rigid formations’ closed-loop dynamics, it is challenging to determine the attraction region of the locally convergent formations [1], [26].
Motivated by the aforementioned drawbacks, we aim to achieve the formation maneuvering of angle rigid formations with global convergence, where the agents can have their own local coordinate frames, and the maneuvering motions include translation, rotation and scaling. Different from the maneuvering approaches in [7], [25], [27], we employ angle-induced linear equations in 2D triangles and 3D tetrahedra to designlinearformation maneuvering laws in 2D and 3D, respectively. We consider that the agents are governed by doubleintegrator dynamics and the available sensor measurements are relative positions and velocities. Compared with the existing results, the main contributions of this paper are summarized as follows:
1) Compared with relative position-constrained, distanceconstrained and bearing-constrained formation maneuvering approaches, the proposed angle-constrained formation maneuvering laws enable the maneuvering motions of simultaneous translation, rotation and scaling. Compared with relative position-constrained and bearing-constrained formations which require agents to have aligned coordinate frames, angle rigid formations allow agents to have non-aligned local coordinate frames.
2) Compared with the existing 2D angle-constrained formation maneuvering laws guaranteeing local convergence[7], [25] and angle-constrained flocking law guaranteeing almost global convergence [27], both of our proposed 2D and 3D angle-constrained formation maneuvering laws have global convergence guarantees.
3) Although both the angle-displacement [8] and affine [5],[28], [29] formation maneuvering approaches enable the maneuvering motions of simultaneous translation, rotation and scaling, the number of leaders required for maneuvering motion control in these works is higher than that of our work which only requires 2 leaders in both 2D and 3D cases.Specifically, the number of leaders should be at least 3 for the algorithms in [5], [29] in 2D, while at least 4 for the algorithms in [5], [8], [29] in 3D.
The rest of the paper is organized as follows. Section II presents the preliminary findings. Sections III and IV introduce the maneuvering strategies of angle rigid formations in 2D and 3D, respectively. Some discussion is conducted in Section V. Simulation results are provided in Section VI.
II. PRELIMINARIES
A. Notations

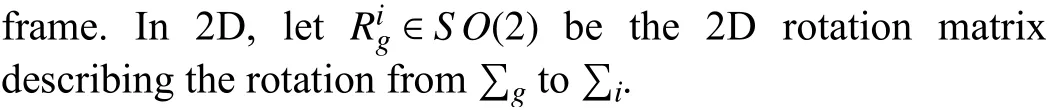
B. Angle Rigid Formations


C. Problem Formulation

III. MANEUVERING 2D ANGLE RIGID FORMATIONS

A. Angle-Induced Linear Equations in Triangles

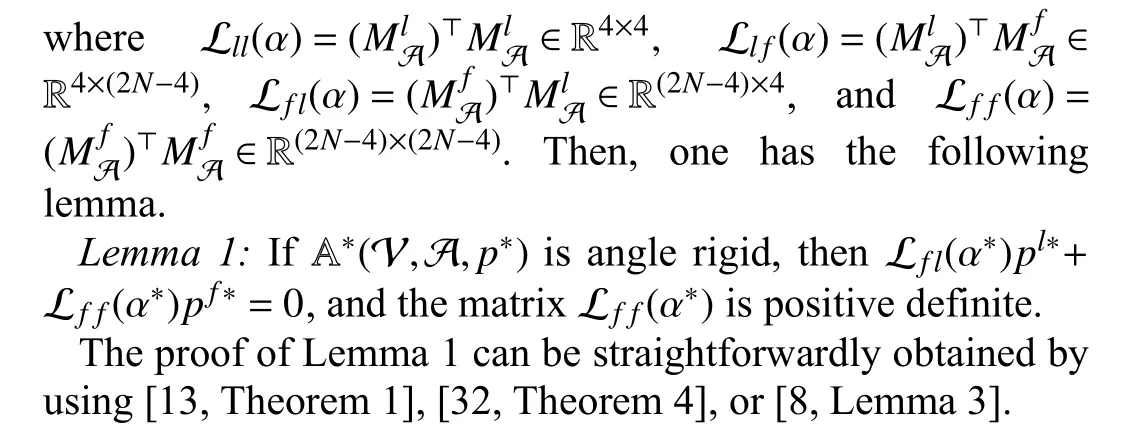
B. Maneuvering Control for the Case of Leaders With Constant Velocities




C. Maneuvering Control for the Case Of Leaders With Time-Varying Velocities


IV. MANEUVERING 3D ANGLE RIGID FORMATIONS
To globally maneuver 3D angle rigid formations by employing angle-induced linear equations, it has been demonstrated in [8] that the construction of each angle-induced linear equation needs to associate at least five agents. This indicates that each agent should have relative position measurements with respect to at least four neighbors. To reduce the number of neighbors that each agent should have, we propose to associate only four agents to construct an angle-induced linear equation under the following assumption.
Assumption 1:Assume in 3D that all the agents’ coordinate frames have a commonZdirection.
Different from [35], [36] where an additional virtual coordinate is assigned to each agent, Assumption 1 practically requires the agents to have the sensing capability of the direction of the globalZ-axis, which can be fulfilled by equipping each agent with a gravity sensor or extracting a common vertical direction via image processing [37]. In the follow-up subsections, we first introduce an angle-induced linear equation established on a tetrahedron, then define the desiredZ-weakly angle rigid formation, and finally design the formation maneuvering law for the followers.
A. Angle-Induced Linear Equations in Tetrahedra


Fig. 1. Establish an angle-induced linear equation for 1234.



B. Desired Z-Weakly Angle Rigid Formations and Their Properties



C. Formation Maneuvering Algorithm Design in 3D



V. ExTENSION TO LAGRANGIAN DYNAMICS AND MINIMUM NUMBER OF ANGLE CONSTRAINTS
A. Formation Maneuvering With Lagrangian Agent Dynamics

B. Construction of Desired Angle Rigid Formations by Minimum Number of Angle Constraints


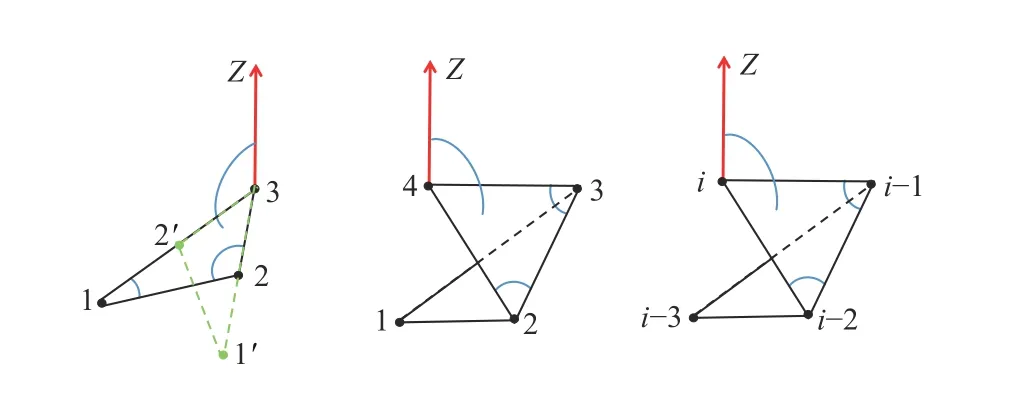
Fig. 2. Construct Z-weakly angle rigid formations by minimum number of angle constraints.
VI. SIMULATION ExAMPLES
This section presents two simulation examples with 4 followers to validate the effectiveness of the proposed formation maneuvering algorithms in 2D and 3D, respectively.
A. Formation Maneuvering in 2D Under Controller (15)
In this simulation, we consider agents 1 and 2 as leaders and agents 3 to 6 as followers. The agents’ initial states are:p1(0)=[−1;−3],p2(0)=[1;−3],p3(0)=[0.4;−4.6],p4(0)=[1.1;−5],p5(0)=[−2;−3.7],p6(0)=[2;−3.5],p˙1(0)=[0;1],p˙2(0)=[0;1],p˙3(0)=[0.1;−0.1],p˙4(0)=[0.2;0.1],p˙5(0)=[−0.1;−0.1],p˙6(0)=[0.4;−0.3]. The desired formation is shown in Fig. 3. The control gains arekp=3,kv=12. We assume that the two leaders have the capability of autonomously maneuvering through a 2D unknown environment with obstacles, which can be achieved by using high-level motion planning algorithms. This simulation uses a polynomial form to plan the maneuvering parameters [29, Section V.B]. The agents’ moving trajectories are shown in Fig. 4, which include translational, rotational and scaling maneuvering. The evolution of angle errors is shown in Fig. 5, which converge to zero. The angle errors are observed to be nonzero during the maneuvering process because the leaders have timevarying velocity and the followers only execute (16).
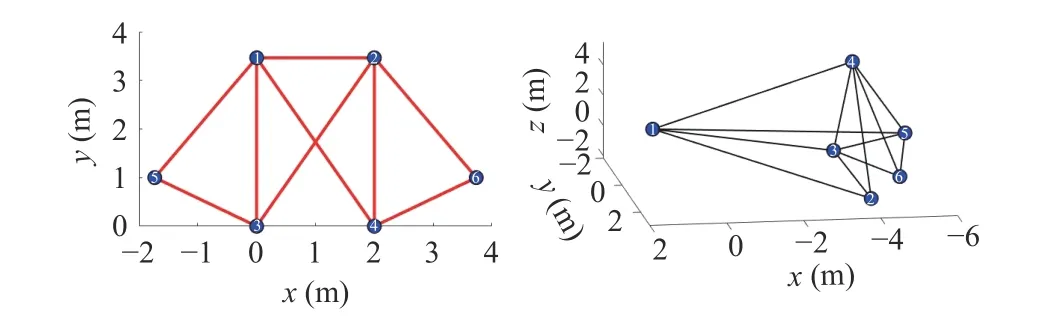
Fig. 3. The desired formations in 2D and 3D.

Fig. 4. Formation maneuvering trajectories in 2D under (15).
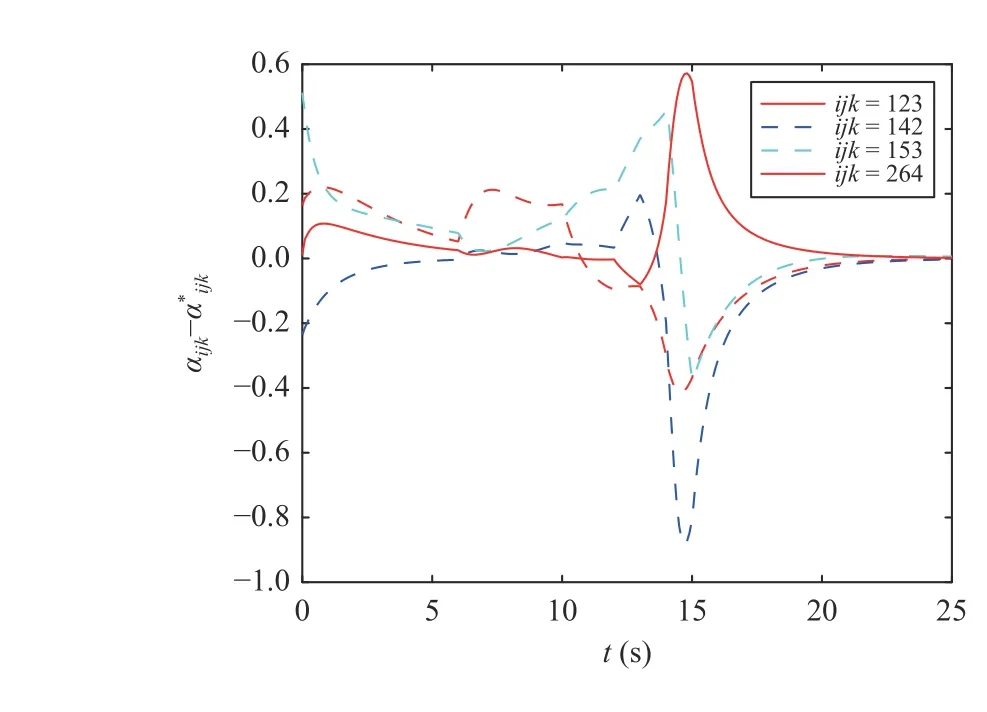
Fig. 5. Evolution of angle errors in 2D under (15).
B. Formation Maneuvering in 2D Under the Sliding Mode Controller (20)
In this simulation, we use the same initial states and desired formation as those in Section VI-A. The control gains arekp=6,kv=1,γ1=5,k1=10. The simulation results are shown in Figs. 6 and 7. Compared with Figs. 4 and 5, the convergence speed is faster and the overshoot is larger in Figs. 6 and 7.
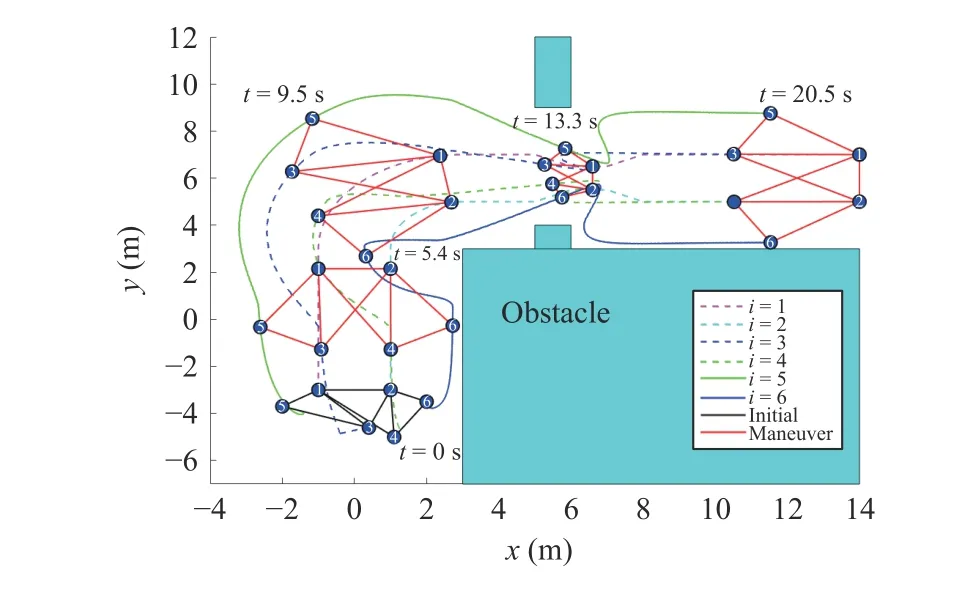
Fig. 6. Formation maneuvering trajectories in 2D under (20).
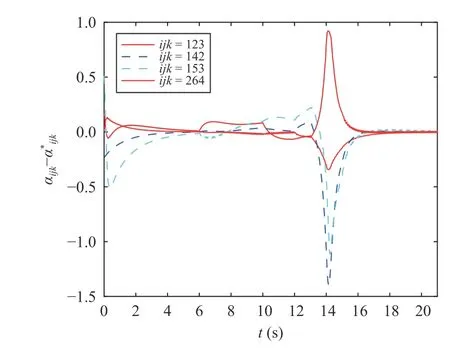
Fig. 7. Evolution of angle errors in 2D under (20).
C. Formation Maneuvering in 3D Under Controller (40)

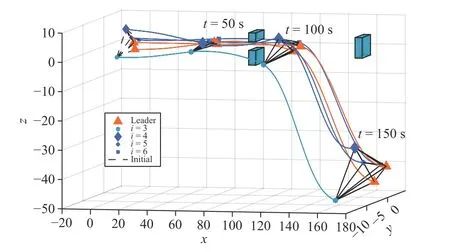
Fig. 8. Formation maneuvering trajectories in 3D under (40).
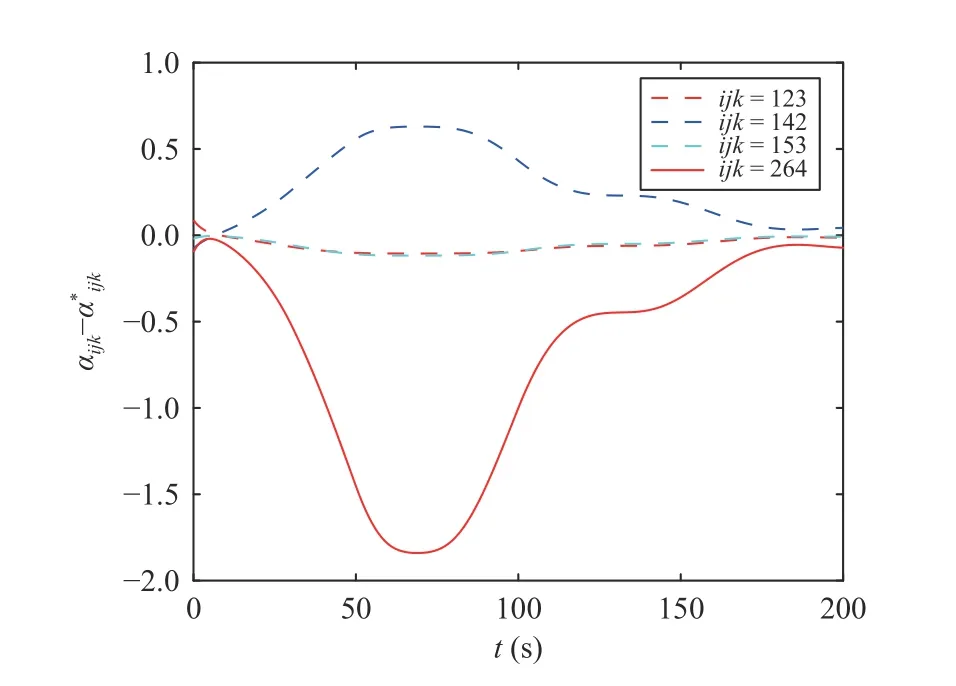
Fig. 9. Evolution of angle errors in 3D under (40).
VII. CONCLUSION
This paper has successfully achieved the maneuvering of angle rigid multi-agent formations in 2D and 3D with global convergence guarantees. For the 2D case, a formation algorithm has been designed to globally maneuver angle rigid formations using only relative position and velocity measurements in agents’ local coordinate frames. For the 3D case, we have established angle-induced linear equations by assuming that all the agents have a commonZdirection. Then,we have proposed a formation algorithm to maneuverZweakly angle rigid formations, where the number of each agent’s required neighbors is reduced to three.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Consensus Control of Multi-Agent Systems Using Fault-Estimation-in-the-Loop:Dynamic Event-Triggered Case
- A PD-Type State-Dependent Riccati Equation With Iterative Learning Augmentation for Mechanical Systems
- Finite-Time Stabilization of Linear Systems With Input Constraints by Event-Triggered Control
- Exploring the Effectiveness of Gesture Interaction in Driver Assistance Systems via Virtual Reality
- Domain Adaptive Semantic Segmentation via Entropy-Ranking and Uncertain Learning-Based Self-Training
- Position Encoding Based Convolutional Neural Networks for Machine Remaining Useful Life Prediction
