降雨作用下三峡库区秭归谭家湾滑坡监测预警研究
2022-08-12张海艳简文星杨新志
张海艳,简文星*,杨 涛,杨新志,沈 铭,李 喜
(1.中国地质大学(武汉) 工程学院,湖北 武汉 430074;2.资源与生态环境地质湖北省重点实验室,湖北 武汉 430034;3.湖北省地质环境总站灾害地质调查监测中心,湖北 武汉 430034)
滑坡灾害在我国具有广泛分布的特点,是我国主要的地质灾害之一,其失稳破坏的后果严重威胁到了人民的生命和财产安全。因此,开展滑坡防治研究具有重要的经济和社会效益。物理模型试验[1-2]和数值模拟方法[3-4]是滑坡灾害防治研究中的常用方法,而依据现场滑坡位移监测数据开展滑坡灾害监测预警研究的方法也是减少滑坡灾害损失的有效手段。由于降雨是滑坡灾害诸多诱发因素中的重要因素[5-7],许多学者致力于开展对降雨作用下滑坡灾害的预警研究[8-10]。
许多学者通过对滑坡位移与降雨的监测数据进行分析,得到了降雨诱发型滑坡位移-降雨间的响应关系。如彭令等[11]通过对白家包滑坡位移和裂缝监测数据的详细分析,认为降雨强度和库水位下降速率是滑坡位移波动的关键因子;胡畅等[12]利用Apriori算法对树坪滑坡位移与诱发因素之间的关系进行挖掘,认为降雨虽然是次要诱发因素,但其影响会随着坡体裂缝的扩张逐渐增强;Yao等[13]利用粗糙集理论对滑坡位移监测序列进行了分析,得到滑坡的主控因素为库水位变动和降雨;Li等[14]基于降雨、地表变形等多点监测数据,利用智能合约算法实现了无人干预的高速公路滑坡智能分区。基于实际监测数据的分析结果更能准确地反映出滑坡实际的变形情况,以及滑坡位移对降雨表现出来的响应特征。
降雨诱发型滑坡灾害的预警方法研究主要分为以内部因素为主、以外部因素为主和以监测为主三类。
以内部因素为主的预警方法主要考虑地质条件对滑坡稳定性的影响,通过对边坡地质条件的分析建立理论模型以对滑坡灾害进行预测预警[15-16],但该方法的结论主要是通过理论推导所得,具有较强的理论性,而并未经过实践验证,因此预警时效性较差。以外部因素为主的预警方法通常以降雨这一诱导因素作为滑坡灾害预警的指标。Caine等[17]在1980年首次对降雨阈值的概念进行了重要拓展,基于世界73个降雨诱发型滑坡和泥石流的数据,建立了被广泛应用的降雨强度(I)和降雨时间(D)模型,但由于该模型样本数据离散性太大,模型的预警效率较低,一些学者对其进行了多次改进[18-19];高华喜等[20]通过统计分析深圳地区降雨和滑坡资料,提出了该区域滑坡降雨预警阈值;胡涛等[21]基于思南县滑坡和降雨的相关资料,建立了平均有效降雨强度(EI)和降雨时间(D)的预警模型,并将其结果与滑坡易发性分区图进行叠加后得到了滑坡危险性预警等级分区图。然而,仅考虑单一降雨因素的滑坡预警会增加误判的可能性,而考虑多因素的滑坡综合预警能显著提升预警的精度。在以监测为主的预警方法中,滑坡位移监测主导的预警模型取得了较好的效果,因为滑坡位移是判断滑坡是否稳定的最直观因素。日本学者斋藤基于岩土体蠕变理论提出了著名的斋藤曲线,将滑坡变形过程划分为初始变形阶段、等速变形阶段和加速变形阶段[22]。在此基础上其他学者针对滑坡位移变形阶段也展开了深入研究,提出了许多滑坡灾害预警模型,如Voight[23]和Fukuzone[24]进一步研究了滑坡在加速变形阶段中速度与加速度之间的关系;王家鼎等[25]根据滑坡位移-时间曲线的切线角变化特征对滑坡灾害进行了预测预报;许强等[26]考虑横、纵坐标单位不统一导致的结果误差,提出了改进的切线角及对应的滑坡预警模型。
由于滑坡的变形特征在区域范围和单体范围内都表现出了显著的差异性,仅用一套预警模型对整个区域进行预警,往往会出现许多误报和漏报的现象,所以根据滑坡不同变形区域来建立滑坡预警模型以提高滑坡监测预警的精细化程度,是当下滑坡监测预警研究中亟需解决的问题。为此,本文以三峡库区秭归谭家湾滑坡为例,通过对滑坡位移和降雨监测数据的分析,得到滑坡各位移监测点变形与降雨间的相关性,并依据滑坡位移序列间的相似性对滑坡变形进行空间上的分区,再从时间尺度上说明滑坡不同变形区域变形程度的差异性,最终确定滑坡不同区域的预警关键指标和相应阈值,并结合现场巡查的滑坡宏观变形建立一套基于滑坡位移降雨响应的4级动态综合预警模型,可为该区域内其他相似滑坡的监测预警提供参考。
1 谭家湾滑坡监测系统布设
1. 1 谭家湾滑坡概况
谭家湾滑坡位于秭归县水田坝乡,位于长江一级支流右岸斜坡地段,大地坐标为东经110°40′27.3″,北纬31°04′16.4″,属于侏罗系砂页岩组成的侵蚀构造低山地貌,山体高程为500~1 000 m,地势南西高北东低。从谭家湾滑坡2-2′地质剖面(见图1)可以看出,滑坡体为一典型的圈椅状凹槽地形[27],平面形态呈“舌”型,滑坡区后缘位于基岩陡壁,前缘直抵河流,左右两侧以冲沟为界,总体坡向为64°,山坡上多为林地。滑坡纵长约为440 m,平均宽约为295 m,体积约为282.5×104m3,面积约为11.3×104m2,平均厚度为25 m,滑体在两冲沟之间呈不均匀分布,厚度不一。
谭家湾滑坡为典型的堆积层滑坡,滑体物质主要为第四系残坡积含碎石粉质黏土,滑带主要成分为含砾粉质黏土,强度较低,遇水极易软化,滑床为泥质粉砂岩,与石英砂岩不等厚互层,顺坡向倾斜。
1. 2 谭家湾滑坡综合监测系统
谭家湾滑坡布设的监测系统以地表位移、降雨量、地下水水位的监测为主,以深部位移、墙面裂缝位移、岩土动力学参数的监测为辅,是一套具有针对性、多层次、多手段、多仪器的自动化实时监测系统。该监测系统由位移监测、孕灾环境因素监测、岩土体动力学参数监测和非接触性三维模型监测4个部分组成,具体监测内容及设备见表1,监测网点布设见图2。

图1 谭家湾滑坡2-2′地质剖面图Fig.1 Geologic profile 2-2′ of Tanjiawan landslide

图2 谭家湾滑坡监测网点布设图Fig.2 Monitoring network of Tanjiawan landslide

表1 谭家湾滑坡监测内容及设备
2 谭家湾滑坡活动与降雨的相关性分析
2. 1 研究区降雨特点
秭归县地处亚热带大陆性季风气候区,气候温和,雨量充沛,年降雨量一般为950~1 590 mm,多年平均降雨量为1 493.2 mm。该地区雨季多发暴雨,降雨主要集中在4~10月份,一日最大降雨量达358 mm,月平均降雨量为150.0~457.6 mm。通过统计分析谭家湾滑坡监测系统所采集的2020年降雨和滑坡位移数据,可得到当年滑坡位移与降雨的关系,见表2和图3。
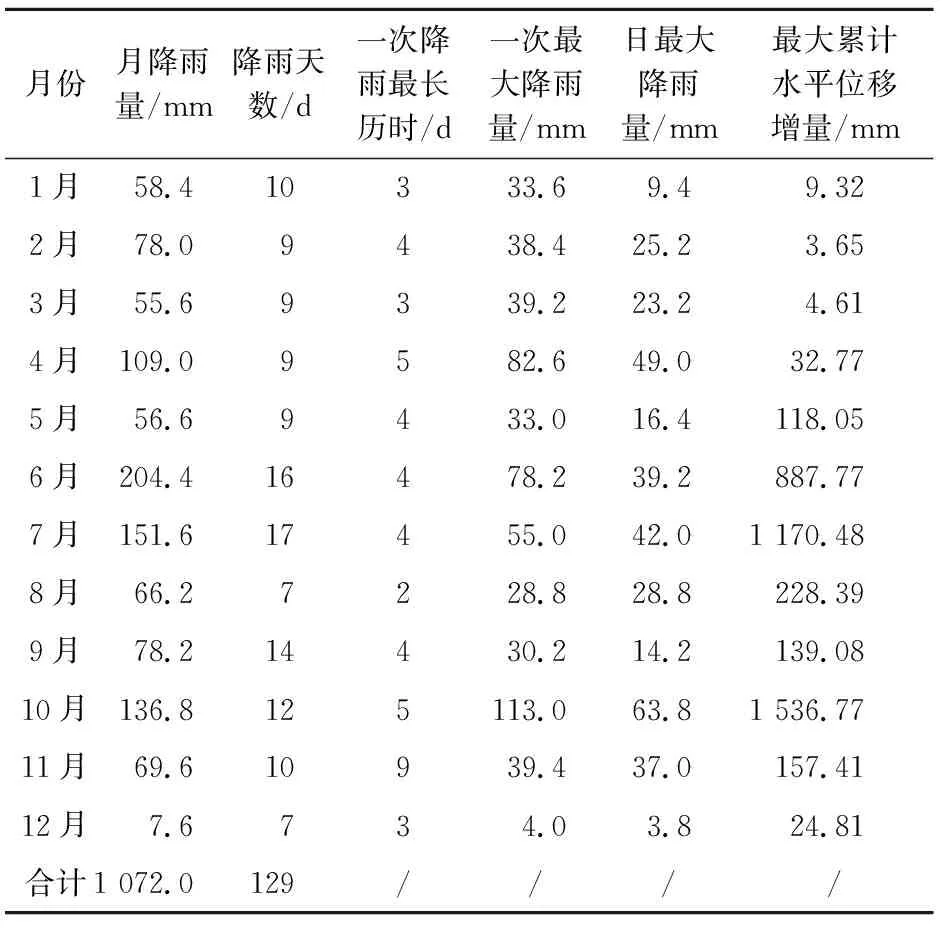
表2 2020年谭家湾滑坡位移与降雨的关系统计表
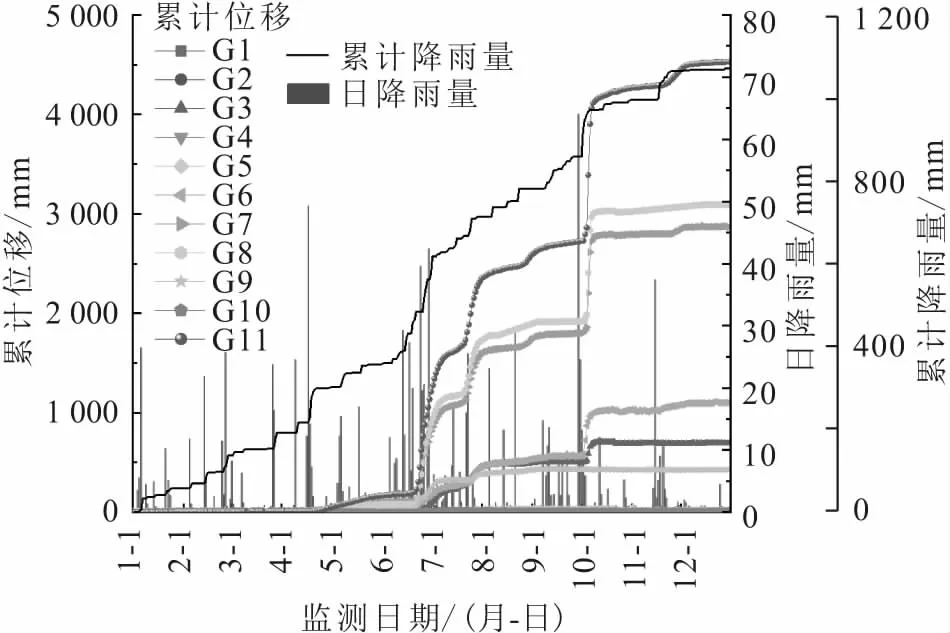
图3 2020年谭家湾滑坡位移与降雨的关系图Fig.3 Relationship between displacement and rainfall of Tanjiawan landslide in 2020
由表2和图3可知:谭家湾滑坡2020年全年累计降雨共129 d,累计降雨量为1 072.0 mm,最大日降雨量为63.8 mm(10月2日),最大月降雨量为204.4 mm(6月),主要降雨量集中在4~10月份,累计水平位移变化主要集中在5~10月份,整体而言,滑坡变形的季节性与降雨的季节性较吻合;4月份的降雨虽然也比较集中,但由于滑坡在2019年夏季发生过一次较大的变形[28],在此之后滑坡一直保持较稳定状态,再加之2019年整体降雨不多,所以4月份最大累计水平位移增量较小,该滑坡未发生较明显的变形。由于谭家湾滑坡距离长江较远,滑坡前缘河流水位年波动幅度在3~4 m左右,受三峡库区水位周期性调动的影响较弱[29],因此谭家湾滑坡属于典型的降雨诱发型堆积层滑坡。
2. 2 滑坡位移与降雨量间的皮尔逊相关分析
上面定性判断出谭家湾滑坡变形季节性与降雨季节性较吻合,为了能更清晰地研究谭家湾滑坡的位移变化与降雨因素之间的相关性,本文采用皮尔逊相关分析法对滑坡各监测点的累计位移与累计降雨量之间的相关性进行了定量分析。
皮尔逊相关分析法主要利用积矩相关系数来反映数据之间的相关性水平,该系数定义为两列数据的协方差与每列数据的标准差之比,可表示为
(1)
其中:r为皮尔逊相关系数;cov(X,Y)为变量X和Y的协方差,即度量两个随机变量协同变化程度的方差;σX、σY分别为变量X、Y的标准差。
当|r|≤1且|r|越接近1,表明两个变量X和Y之间的相关程度越高;当|r|≥0.8时,两个变量间为高度相关;当0.5≤|r|<0.8时,两个变量间为中度相关;当0.3≤|r|<0.5时,两个变量间为低度相关;当|r|<0.3时,说明两个变量之间的相关性极弱,基本不相关[20]。
本文采用SPSS 24.0软件对谭家湾滑坡累计位移与累计降雨量进行皮尔逊相关分析,其分析结果见表3。

表3 谭家湾滑坡累计位移与累计降雨量的皮尔逊相关系数
由表3可知:5~10月份为汛期,其分析结果与全年分析结果基本一致,而4月、11月和12月滑坡各监测点分析结果有所不同,出现了较多的空值,其原因可归纳为一是因监测数据连续性低导致数据补差后的分析结果失真,故相应的相关系数被去掉,二是滑坡监测点全年较为稳定,整体位移较小,说明受降雨的影响非常小,故其相关系数无参考价值;4~12月的滑坡各监测点累计位移与累计降雨量的相关性系数表明,滑坡各监测点累计位移序列与累计降雨量序列在该时期内呈现出总体相关、区域差异的特征。尽管总体而言,汛期G1~G11监测点的累计位移与累计降雨量都表现出相关性,但由于G1、G2、G4、G5和G10监测点所处滑面的倾角较缓,裂隙不发育,历史变形较小,所以其累计位移对累计降雨量的响应相对较弱,两者监测数据呈中低度相关;而G3、G6、G7、G8、G9和G11监测点在滑面较陡的位置,部分点因滑坡历史变形较大而裂缝发育,给降雨入渗提供了良好通道,所以这些区域易受降雨的影响产生变形,两者监测数据呈高度相关。
整体而言,谭家湾滑坡累计位移与累计降雨量之间具有良好的相关性,但相关性的强弱体现出明显的空间差异性,如滑坡中前缘(G7、G8和G11监测点)累计位移与降雨量的相关性最强,滑坡中后缘(G3和G6监测点)及左侧冲沟后缘(G9监测点)累计位移与降雨量的相关性稍次之,滑坡侧边区域(G2、G5和G10监测点)累计位移与累计降雨量的相关性相对较弱。由此可见,谭家湾滑坡不稳定区域主要分布在滑坡前后两公路中间区域和左侧冲沟后缘。
3 谭家湾滑坡变形的时空分布特征
3. 1 谭家湾滑坡变形的空间分布特征分析
谭家湾滑坡各个监测点变形数据表现出变形规律的差异,反映出了滑坡变形特征的区域差异性,故本文开展对该滑坡各监测点位移序列间的相似性分析,并基于所得到的位移序列间关联程度进行滑坡变形区域的区块划分,为建立考虑变形区域差异性的预警模型奠定基础。
为了能更直观地表述监测点位移序列间的相似性概念,现假设有4个监测点位移序列(见图4),其中位移序列1与位移序列2的相似性明显高于位移序列1与位移序列3或4,位移序列3与位移序列4的相似性明显高于位移序列3与位移序列1或2。所以,可将这4组位移序列划分为两组,即位移序列1与位移序列2为一组,位移序列3与位移序列4为一组,每组序列变化“步调”基本一致,如果每组的两个监测点来自于同一滑坡不同部位,则可初步认为同一组的监测点可能具有相似的滑动机制。

图4 位移序列间相似性关系分析图Fig.4 Analysis diagram of similarity relation between displacement sequences
为了定量描述位移序列间的相似性,本文定义了位移序列间的“非相似度”(见图5)。假定有k个位移序列,现从k个位移序列中选出一个位移序列yj,为了研究其与标准位移序列y0之间的联系程度,可通过基于序列间距离定义的非相似度来衡量,两个位移序列之间在i时刻的距离可表示为
(2)
其中,Δyj(i)=|y0(i)-yj(i)|。
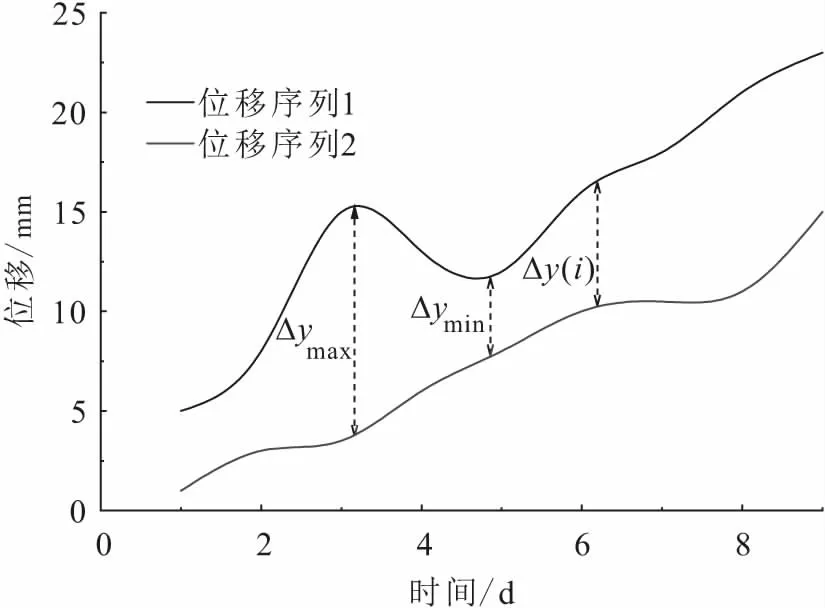
图5 非相似度定义图Fig.5 Definition of dissimilarity
两个序列间的非相似度即为所有时刻距离的均值,即:
(3)
通过对图3谭家湾滑坡的位移和降雨数据进行分析可以发现:位于滑坡后缘滑面较缓处的G1、G2、G5监测点全年累计位移最大未超过35 mm,该区域整体较为稳定,并且G4和G10监测点分别位于滑坡右侧和左侧的冲沟附近,处于稳定状态,因此在相似性分析中不考虑这5个点的位移数据;而位移数据对降雨响应最快且增幅最为明显的是G11监测点,这说明G11监测点位移变化与降雨间具有良好的相关性,因此将G11监测点位移序列设置为标准位移序列y0,计算得到G3、G6、G7、G8、G9监测点与G11监测点位移序列间的非相似度,见表4。
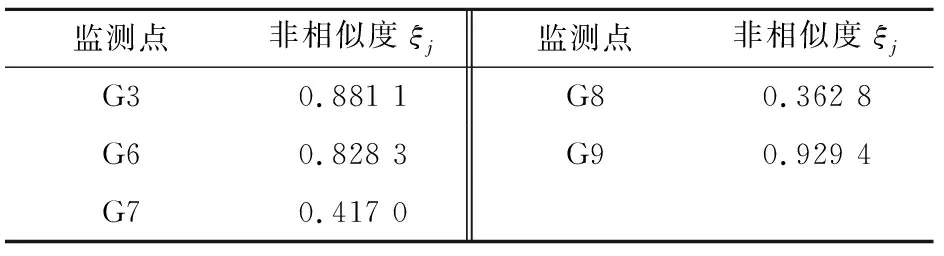
表4 谭家湾滑坡不同监测点与G11监测点位移序列间的非相似度
结合表4中所选定监测点位移序列间的非相似度,按照“非相似度越大相似性越低”的原则,将谭家湾滑坡在空间上划分为3组变形区:以G7、G8和G11监测点为第一组,代表滑坡中前缘主要变形区(见图6中①);以G3和G6监测点为第二组,代表滑坡中后缘变形扩展区域(见图6中②);G9监测点单独为第三组,代表滑坡左侧冲沟局部变形区(见图6中③)。
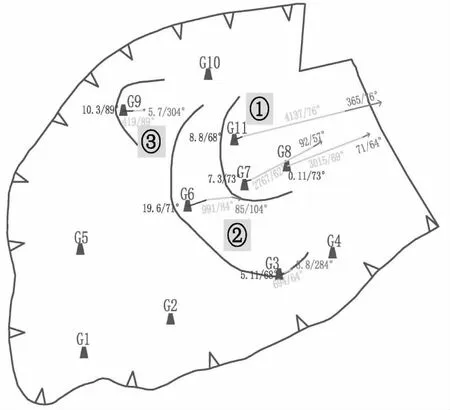
图6 谭家湾滑坡变形分区及位移矢量图Fig.6 Deformation zone and displacement vector map of Tanjiawan landslide注:图中5.11/68°表示滑坡位移量为5.11 mm、滑坡位移方向为68°。
结合图3中滑坡位移与降雨的关系可以观察到谭家湾滑坡中前缘整体变形程度不仅要强于滑坡中后缘变形拓展区和左侧冲沟变形区,而且变形的降雨响应幅度较后两者也更剧烈:滑坡第一变形区的累计位移最大达4 525 mm,最大一次加速变形量达到1 450 mm,而滑坡第二、三变形区的累计位移最大仅有1 100 mm,同一时间段内最大一次加速变形量也仅为451 mm,这说明3个区域的累计位移时间曲线在同一坐标尺度下呈现出了明显的聚类分组现象。
3. 2 谭家湾滑坡变形的时间分布特征分析
谭家湾滑坡的变形不仅表现出了空间分区的特征,其阶跃变形的现象也表现出时间分段的特点。根据表2和图3中谭家湾滑坡的变形幅度特征,结合降雨季节的划分,可将2020年该滑坡的变形分为3个时段(见图6):
(1) 第一时段(1月2日—4月22日)是非汛期基本稳定阶段,其位移矢量用蓝色线段表示。在该时段内,各个监测点尚未产生明显的位移,滑坡处于稳定状态。
(2) 第二时段(4月23日—10月11日)是汛期变形阶段,其位移矢量用青色线段表示。在该时段内,滑坡先后出现了5次不同幅度的位移抬升,也即为4月末汛期后充沛降雨导致的第一次阶跃变形和进一步增大的降雨量导致的4次幅度相对较大的阶跃变形。通过对这5次阶跃变形曲线特征进行分析可以观察到,每一次阶跃变形均经历了前等速变形阶段、加速变形阶段和后等速变形阶段[30],且加速变形阶段稍滞后于降雨事件的发生。
(3) 第三时段(10月12日—12月31日)是非汛期变形后阶段,其位移矢量用绿色线段表示。在该时段内,由于降雨稀少,滑坡各个监测点在经历汛期大变形之后恢复到了基本稳定状态,只有在发生强降雨后,其累计位移曲线才会出现小幅度抬升;同时,该时段内滑坡位移对降雨的响应关系有所不同,该阶段滑坡位移对降雨响应的滞后时间较第二时段稍长。
整体而言,谭家湾滑坡变形的阶段性与降雨的季节性相吻合,且位移变化与降雨之间存在一定的滞后期。其原因是滑坡位移对降雨的响应时间和响应幅度除了受滑坡本身地质条件的影响外,还与降雨的雨量、雨型和历时密切相关。
4 谭家湾滑坡综合动态预警模型建立
上节分析表明,阶跃型位移特征的滑坡会出现数次加速阶段,这无疑给滑坡的临滑判断造成很大的困难。为了更加安全、有效地对谭家湾滑坡这一类具有明显阶跃特征位移曲线的降雨型滑坡进行预警,本文从多参数分级预警和动态预警的角度出发,建立了从降雨量到滑坡位移响应特征的综合预警判据,并建立了考虑综合降雨量、位移速率(改进切线角)和现场裂缝分期配套特征等多因素判据的滑坡综合动态预警模型。
4. 1 降雨量阈值确定
由前述内容可知,谭家湾滑坡变形受前期降雨和当次降雨的影响,且滑坡位移变化滞后于降雨事件的发生。为了确定该滑坡位移滞后时间t,降雨量序列选取为2020年谭家湾滑坡日降雨量序列,位移速率序列选取为向前平移t天的该滑坡G11监测点日位移速率序列,对两者开展皮尔逊相关分析,其分析结果见表5。

表5 不同滞后时间下谭家湾滑坡G11监测点日位移速率与降雨量的皮尔逊相关系数
由表5可知:日位移速率与降雨量的相关性从t=1 d到t=6 d呈现出先增大后减小的趋势,在t=3 d时达到最大,且在t=5 d时仍未降低到可忽略不计的程度。因此,将谭家湾滑坡位移对降雨的滞后时间确定为3 d,该时间也与当地居民长期观察到的现象基本一致。
将谭家湾滑坡变形分为若干等速变形阶段和加速变形阶段,滑坡位移变化受前期降雨和当次降雨的影响,影响时间为滑坡整个加速变形阶段。前期降雨中诱发滑坡发生的那部分降雨为有效降雨,且前期有效降雨量随着时间增长一般呈幂指数形式衰减[31]:
Re=αR1+α2R2+…+αnRn
(4)
其中:Re为前期有效降雨量;Rn为前n天降雨量(mm);α为降雨衰减系数,一般为0.8。
因滑坡位移受前3天降雨的影响最大,故仅考虑加速变形阶段前3天的前期降雨量。以谭家湾滑坡G11监测点为代表计算出各个加速变形区间的前期降雨量Re和当次降雨量R0,其结果见表6。
由表6可知,谭家湾滑坡加速变形期间的当次降雨量范围为21.40~206.20 mm,前期降雨量范围为17.47~51.04 mm,故取整值,当次降雨量阈值(R01)为21 mm,前期降雨量阈值(Re1)为17 mm。
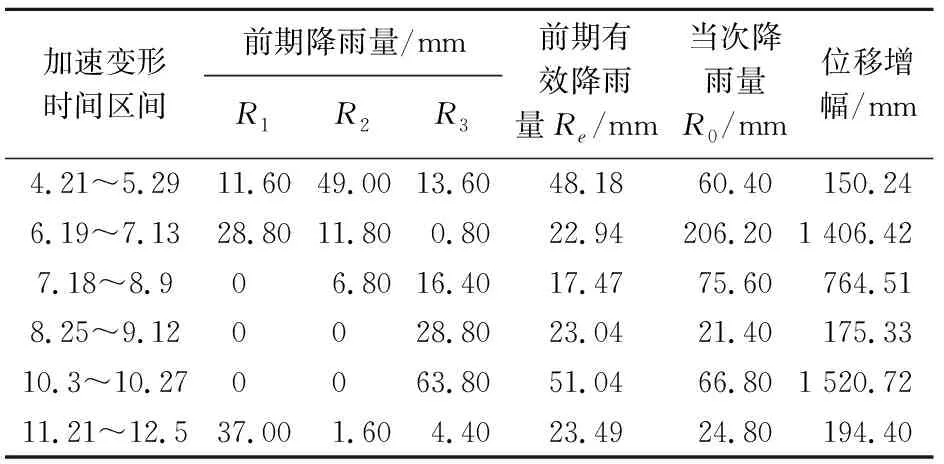
表6 谭家湾滑坡G11监测点加速变形时间区间对应的降雨信息
4. 2 滑坡位移速率阈值确定
根据历史监测数据和现场巡查推测[28],谭家湾滑坡初始变形发生于2007年至2009年期间,此后的监测数据表明该滑坡一直处于基本稳定状态。一直到2014年开始,滑坡受诱发因素的影响活动频繁,导致位移监测曲线出现了明显的阶跃特征。如图7所示:当滑坡的位移速率突破等速变形阶段的变形速率时,滑坡可能即将进入加速变形阶段;而当滑坡加速变形阶段的位移速率开始下跌时,滑坡则可能回到等速变形阶段,这表示位移监测曲线中滑坡位移速率的变化可以直观、有效地反映滑坡稳定性状态的变化。
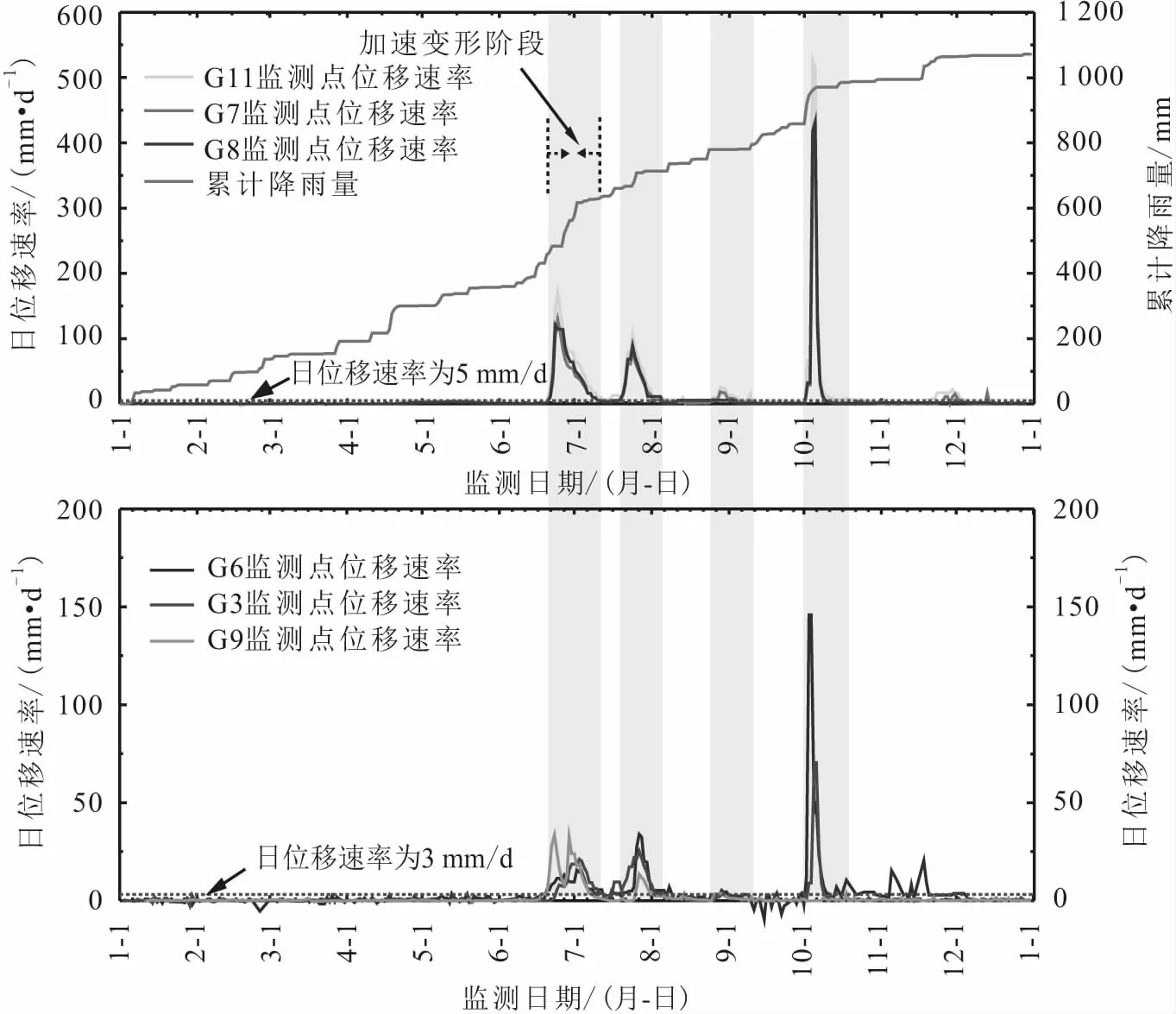
图7 2020年谭家湾滑坡位移速率-时间曲线Fig.7 Displacement rate-time curves of Tanjiawan Landslide in 2020
为了能通过滑坡位移速率判断滑坡目前所处的变形阶段,可通过改进切线角模型[26]来求取进入不同变形阶段前的滑坡位移速率阈值,并将其作为滑坡预警的判据,考虑到滑坡不同区域变形的时空差异性,通过计算滑坡各变形区域的位移速率阈值,以对滑坡进行精细化分区预警。
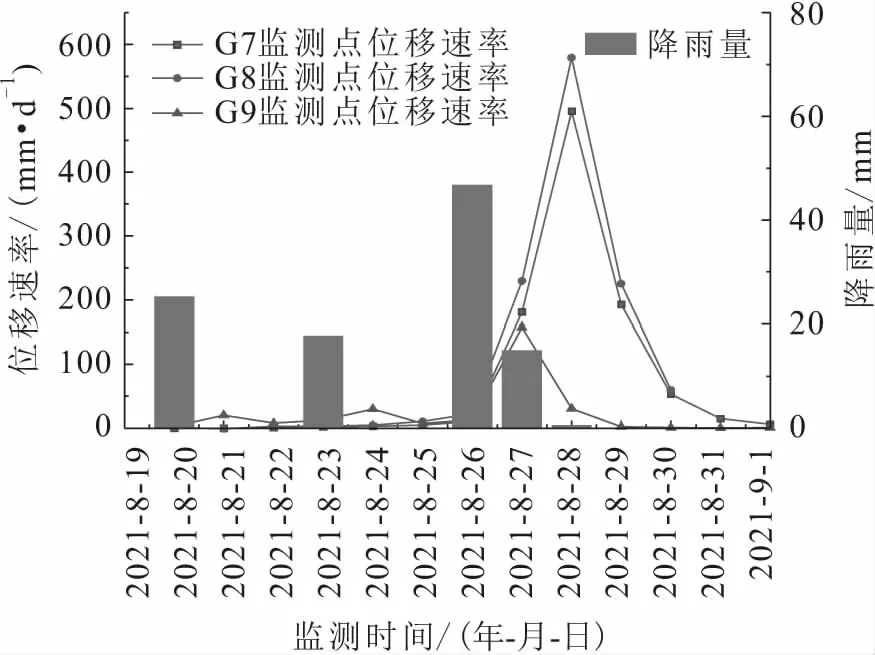
令滑坡位移速率在进入等速变形阶段、中加速变形阶段和加速变形阶段的阈值分别为v1、v2和v3,任意时刻t时滑坡的位移速率为vt,通过对滑坡位移-时间曲线展开分析,进而可判断滑坡目前所处的变形阶段。当vt>v1且位移加速度a>0时,表示滑坡由基本稳定状态进入加速变形状态,其中,v1≤vt 结合前文所述和滑坡现场巡查的结果,在表7中给出滑坡3个变形分组在等速变形阶段、中加速变形阶段和加加速变形阶段的位移速率阈值,并建立谭家湾滑坡由诱发因素到位移响应的综合动态预警模型。具体分析如下: (1) 蓝色预警(注意级):此时滑坡处于初始变形阶段或已经进入等速变形阶段。前期降雨量未超过17 mm,滑坡中前缘主要变形区(G7、G8和G11监测点)vt≤v1=5 mm/d,滑坡中后缘变形拓展区和左侧冲沟局部变形区(G3、G6和G9监测点)vt≤v1=3 mm/d,且位移加速度a≈0,现场新生裂缝开始产生。 (2) 黄色预警(警示级):此时滑坡已经进入加速变形阶段,但尚处于初始加速变形阶段。前期降雨量达到17 mm以上,滑坡各个变形区域的位移速率均超过等速变形速率,但未超过v2(G7、G8和G11监测点为28 mm/d;G3、G6和G9监测点为17mm/d),且变形加速度a>0,现场新生裂缝进一步扩展。 (3) 橙色预警(警戒级):此时滑坡已经由初加速变形阶段转为中加速变形阶段,但未达到加加速阶段即临滑阶段。滑坡各个变形区域的位移速率均已超过v2,但未超过v3(G7、G8和G11监测点为57 mm/d;G3、G6和G9监测点为34 mm/d),且位移加速度a持续增大,现场新生裂缝逐渐拓展延伸并趋于贯通。 (4) 红色预警(警报级):此时滑坡已经进入加加速阶段即临滑阶段。加速期间内的当次降雨量超过21 mm,滑坡各个区域的变形速率均超过v3,现场裂缝相互贯通趋于圈闭。 表7 谭家湾滑坡综合动态预警模型 本文结合2021年8月谭家湾滑坡位移、降雨监测数据对模型进行验证,如图8所示。 图8 2021年8月谭家湾滑坡位移速率-降雨量关系图Fig.8 Displacement rate-rainfall relationship diagram of Tanjiawan landslide in August 2021 由图8可知:2021年8月20日降雨量达到25.2 mm,按照衰减系数计算前期降雨量为20.16 mm,超过了蓝色预警前期降雨量阈值,同时由于当天G9监测点位移速率达到3 mm/d,因此综合发布蓝色预警;随后G9监测点位移速率持续波动,并于8月24日达到最大值30.22 mm/d,但未超过34 mm/d,考虑到加速变形期间当次降雨量为17.8 mm,未超过当次降雨量阈值,且8月24日G7和G8监测点位移速率超过5 mm/d而进入加速变形阶段,因此发布黄色预警;8月26日当日降雨量达到46.8 mm,超过前期和当次降雨量阈值,滑坡各监测点累计位移持续上升,结合现场巡查情况,因此发布黄色预警;8月27日降雨量达到15 mm,滑坡各监测点累计位移均远远超过预警值,结合现场巡查情况,因此发布红色预警。 (1) 谭家湾滑坡是典型的降雨诱发的“阶跃”型堆积层滑坡。该区域内降雨主要集中在每年4~10月份,这也是滑坡位移变化明显的时期。在滑坡累计位移曲线每一次发生“抬升”之前,累计降雨曲线必然会出现一定幅度的增加。 (2) 利用皮尔逊相关分析法对滑坡位移与降雨的相关性进行定量判断的结果表明:滑坡的位移变形与降雨事件之间具有高度相关性,其中滑坡中前缘公路后侧区域(G7、G8和G11监测点)累计位移与累计降雨量的相关性最强,滑坡中后缘公路前侧区域(G3和G6监测点)和左侧冲沟附近(G9)累计位移与累计降雨量的相关性次之,而其他区域基本处于稳定状态。 (3) 利用各个监测点位移序列间的非相似度对谭家湾滑坡的空间变形特征进行了定量分析,按照位移序列的相似性将谭家湾滑坡划分为了3个变形区,同时根据对滑坡位移-降雨间响应关系的研究,定性分析了滑坡位移变形随降雨所表现出来的季节性和滞后性。 (4) 综合谭家湾滑坡的变形特征和现场巡查现象,分区建立了基于滑坡位移-降雨响应的4级综合动态预警模型,得到了滑坡进入加速变形阶段的前期降雨量和当次降雨量的阈值,以及滑坡进入各个变形阶段的位移速率阈值。该模型认为滑坡位移速率一旦超过等速变形速率就很有可能进入加速变形阶段。4. 3 滑坡综合动态预警模型建立

4. 4 模型验证
5 结 论
