基于半监督聚类算法的水利枢纽工程设备自适应PID控制系统

唐顺田

(莒南县石泉湖水库管理所，山东 临沂 276600)

0 引言

水利枢纽指的是水工建筑的综合体，主要修建在河流和渠道地段，且该建筑的类别根据实际情况存在差异，建设水利枢纽的主要目的是保证各项水利工程的兴利除害。水利枢纽主要由挡水、泄水、蓄水以及专门性四类建筑物以及航运、鱼道、交易通道等多类工程组成。水利枢纽在建设过程中，需结合工程设备完成[1]。工程设备指的是，水利枢纽建筑工程中使用的机电设备、金属结构设备以及相关仪器装置等[2]，该类设备在使用和运行过程中通常采用PID控制系统对其运行实行控制[3]，且在该控制过程中，需依据水利枢纽工程设备的数据完成[4]。该控制系统作为一种线性控制，其控制原理简单、应用范围较广，依据误差确定控制量[5]，以此实现目标控制。半监督聚类算法是数据挖掘中的一种常用的聚类算法，其在模式识别、空间数据分析、异常检测以及数据流挖掘等领域均具备良好的应用效果。

为实现PID控制系统的良好控制效果，文献[6]和文献[7]分别对其控制原理实行分析后，研究基于Smith预估器模型和基于MPSO的自适应模糊PID控制。上述方法在控制过程中，对于控制目标数据的利用仍旧存在一定局部性，无法全面利用控制目标的数据，因此，该文为实现PID控制系统的更佳控制效果，研究基于半监督聚类算法的水利枢纽工程设备自适应PID控制系统的自适应控制方法，该方法采用径向基函数神经网络(Radial basis function network，RBF network)对水利枢纽工程设备PID控制系统实行自适应在线调节，并采用蚁群算法对该控制系统实行优化，并在优化过程中，采用半监督聚类算法完成调节参数的聚类，完成调节优化，提升PID控制系统的控制效果。

1 水利枢纽工程设备自适应PID控制系统

1.1 基于RBF network的工程设备自适应PID控制系统

由于水利枢纽工程设备的运行具备多变量、非线性等特点，则基础PID控制系统在控制过程中存在局部性，影响控制效果，因此，该文在采用RBF network模型对PID控制系统实行在线调整，实现PID控制系统参数自适应，提升PID的控制效果[8]。基于RBF network水利枢纽工程设备自适应PID控制系统结构如图1所示。

图1中，rim(k)和ym(k)均表示工程设备的功率，前者对应设备输入参考；后者对应该文设计的控制系统的识别输出；RBF network模型的实时调整参数增量为Δkp，Δki，Δkd表示。RBF network模型为实现对工程设备自适应PID控制系统的在线调节，需对自身权系数实行调整后，对控制系统的误差实行对比[9]，并获取恰当的PID参数，以此能够最大程度实现PID控制系统的控制性优化。

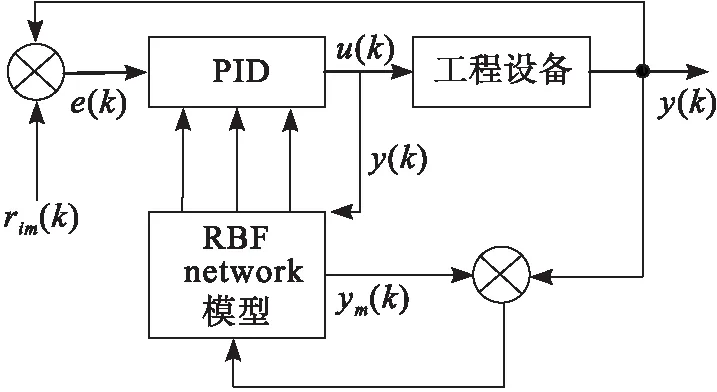
图1 水利枢纽工程设备自适应PID控制系统结构

图1中PID控制系统的设计采用增量式PID控制完成[10]，该控制误差的计算公式为：

e(k)=(k)(rim-y)ψ

(1)

式中：ψ表示控制系数；控制器的输出用u(k)表示，其计算公式为：

e(k-1)]}

(2)

增量型PID控制算法的计算公式为：

(3)

PID控制器的输入计算公式为：

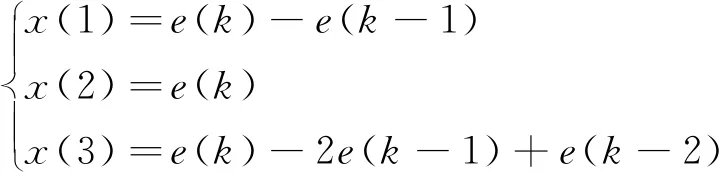
(4)

RBF network模型的性能指标函数为：

E(k)=0.5e(k)2

(5)

Δkp，Δki，Δkd三个参数的增量的调整采用梯度下降法完成，其公式为：

(6)

式中：ηp,ηi,ηd均表示学习速率，对应三个参数，且均属于RBF network模型；x表示该模型的输入向量。

(7)

式中：Cij表示节点中心；ωj表示输出权重；hj表示高斯函数；bj表示基宽带，该值大于零。

基于上述内容可知，采用RBF network模型对PID控制系统实行在线调整，主要是通过自适应的方式实现PID参数的调整，则调整后的PID参数为：

(8)

式中：kp，ki和kd均表示调整后的参数，且将该参数输入至PID控制器中。

1.2 PID控制系统在线调节RBF network模型参数优化

RBF network模型在对PID控制参数实行调整过程中，为了保证调整结果的合理性和最佳性[11]，采用蚁群算法对其实行优化，该优化分为两部分，一是基于半监督聚类算法对RBF network模型的在线调节参数实行聚类；二是采用蚁群算法对聚类结果实行寻优。

1.2.1 PID控制系统在线调节模型参数聚类

该文采用基于层次策略的散布种子中心半监督聚类(scattered seeds medoids clustering，SSMC)算法完成RBF network模型参数聚类，该算法的聚类共分为3步：第一步是采用边缘因子完成RBF network模型参数的在线调节所需的分层处理，将其划分成核心层和边缘层，同时能够完成参数集中离群点和噪声点干扰的处理；第二步是完成核心层聚类，其采用基于散布种子的半监督K-medoids算法实现；第三步以半监督策略为前提，采用分配方式，完成边缘层的簇处理，该处理需在核心层中进行，以此获取在线调节参数的聚类结果[12]。

采用边缘因子在对原始参数集实行分层处理时，需先对边缘因子、边缘点、边缘层、核心点以及核心层实行定义。

第一步：基于边缘因子完成原始参数集的分层

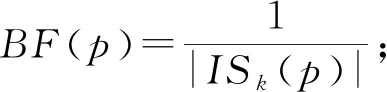
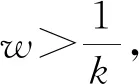
采用边缘因子完成原始参数集的分层处理的步骤如下所述：

输入：原始参数集数D、邻域常数k以及边缘比例因子i。

输出：边缘层BL和核心层CL。

(1)计算各个p对应的BF(p)结果，且p属于D中；

(2)依据所有计算获取的BF(p)结果，对p实行排序，且按照由大到小的顺序完成，采用其中的第int(iN)个值描述t；

(3)完成子集划分，形成子BL，其由边缘点组成，且所有的点对应的BF(p)需大于t，剩余的样本则为核心点，组成CL。

第二步：核心层聚类

为实现该层中参数聚类，获取初始聚类中心的种子，需实现标记参数的初始化处理[13]，其基于散布种子的半监督K-medoids算法完成；为获取标记参数的监督信息，采用半监督约束K-medoids算法实行求解，以此可提升局部空间数据分布信息的挖掘效果。但是由于标记参数在获取过程中具备随机性，其在局部空间内存在重叠现象，分散度较差，因此，采取合并的方式对簇实行处理，并获取合并后的簇中心[14]。合并的条件为：当前簇中所包含的数量小于k、且当前簇类别与标记参数类别的簇种子相等时，详细步骤如下所述：

输入：CL和标记参数集LD。

输出：CL中的参数聚类结果CLr。

(1)设Lpi表示全部的标记参数，且Lpi∈CL∩MD，并位于CL中，对其实行初始化处理后得出簇中心，用ci表示；并采用初始化对Ci={ci}实行处理；

(2)计算全部非标记参数p，并获取与其相似度最高的簇中心[15]，将p划入其中；

(3)判断簇是否符合合并条件，并对合并后的簇中心实行求解以及簇合并处理；

(4)获取每一个Ci以及其均值μi，将与μi之间距离最小的样本实行更新，并定义其为新的聚类中心；

(5)重复上述(2)～(4)步骤，当全部的簇中心不会产生变化后停止；

(6)以Ci中Lpi的信息为以依据完成全部子簇的合并处理，以此获取CLr结果。

第3步：基于半监督策略的边缘层分配

输入：BL和CLr，输出聚类结果C={C1,…,Ck}。

(1)将BL(p)的结果按照由小到大顺序实行排列。

(2)获取边缘层中的第一个样本p，同时在核心层中获取与p之间距离最小的样本q；

(3)设定p和q的簇标记相等，向CLr中划分p；

(4)重复(2)，当BL为空时停止。

1.2.2 基于蚁群算法的PID控制系统调节参数寻优

RBF network模型中Cij和bj的取值直接影响RBF network模型对PID控制系统的在线调整效果，因此，蚁群算法寻优目的即为获取两者的最佳取值，保证在线调整效果。寻优步骤如下所述：

(1)通过初始化获取不用的CLr，且数量为k；

(2)计CLr算和样本输入k的距离；

(3)为获取新的聚类中心，计算分类样本平均值；

(4)过程初始化，在数量为n的样本上部署数量为m的蚂蚁，同时记录蚂蚁的初始位置，且在禁忌表中完成。

(9)

式中：iallowedn表示参数样本，其中不包含禁忌表；Q为正常数。

(5)依据公式(9)的计算结果，获取τij，其属于Xi与聚类中心cj(t)之间，并将cj(t)加入tabum中；

(6)求解Δτij(t+1)，确定Xi的分类依据，即为Xi与cj(t)之间的τij(t)，以此完成Xi分类，新的聚类中心cj(t+1)则可采用分类后Xi的均值描述；

(7)以所有cj(t+1)为依据，计算其相互之间的距离，并完成bj的计算，bj=σdi。其中di表示距离，对应两个聚类中心之间，分别为第i个和与其距离最小的；σ表示重叠系数；Cij=cj(t+1)。

2 测试分析

为测试该文方法对于水利枢纽工程设备PID控制系统的控制优化效果，以某地区的水利枢纽工程中的大型蓄能电站机组为研究对象，获取其PID控制系统1个月的数据为测试数据，采用MATLAB按照图1的控制结构进行仿真测试。

参数设定：RBF network模型的隐含节点数量为8，学习速率取值为0.25，惯性系数取值为0.06，权重分别为0.32、0.4以及0.15；PID控制系统的初始参数kp、ki、kd的取值分别为0.4、0.2、0.4,。蚁群规模为30，最大迭代次数为240次，聚类数量为4，σ取值为1。

为衡量该文方法对PID控制系统的在线调节效果，采用该文方法对实验对象的PID控制系统的kp、ki、kd实行在线调节，自适应调节结果，如图2所示。

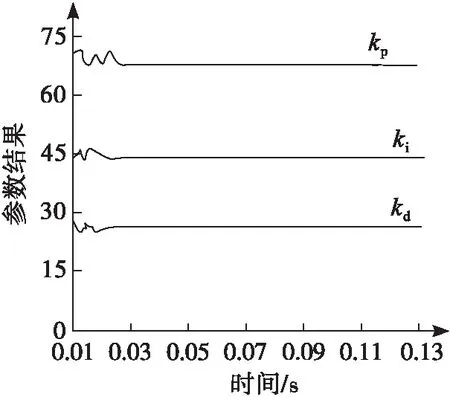
图2 自适应调节测试结果

依据图2结果可知：该文方法在对PID控制系统的kp，ki，kd参数实行调节过程中，3个参数在0.04 s时，则达到稳定状态，自适应曲线不再发生变化。因此，表示该文方法具备良好的在线调节效果，能够快速完成调节动态响应。

为衡量该文方法的聚类效果，采用互信息和兰德指数作为评价指标，测试该文方法在不同比例的监督样本下，两个指标的结果，如图3所示。两个指标的计算公式为：

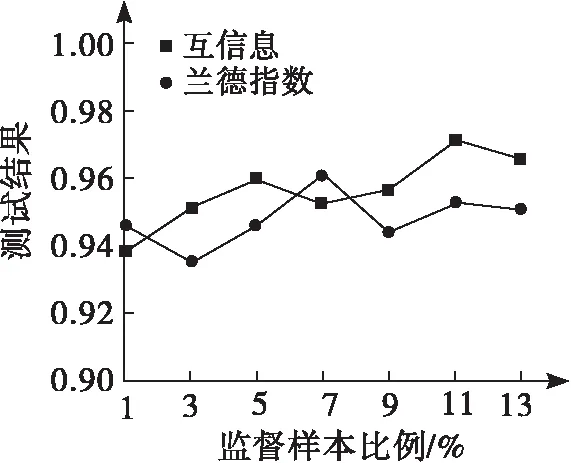
图3 聚类效果测试结果

(10)

(11)

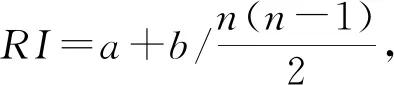
依据图3结果可知：随着监督样本比例的逐渐增加，MI(A,B)和ARI两个指标的测试结果均在0.93以上，最高值分别达到0.97和0.96左右，因此，该文方法聚类效果良好，能够为模型寻优提供可靠的数据依据。

为衡量该文方法对PID控制系统的在线调节效果，以相对值作为衡量标准，测试PID控制系统经过在线调节，在存在干扰和没有干扰两种情况下，PID控制的相对值，该值越接近1表示，控制效果越好，控制过程中，相对值的波动变化越稳定，表示控制效果越佳，如图4所示。

图4 在线调解效果测试结果

依据图4结果可知：经过该文方法在线调节后，PID控制系统在有干扰和无干扰两种情况下的相对值均在0.95以上，并且波动幅度较小，在0.96～0.98的范围内，因此，该文方法可对PID控制系统实行良好的在线调节，最大程度保证PID的控制效果。

水利枢纽工程应用过程中，蓄水是其一个主要的作用，因此，衡量该文方法优化后PID控制系统实行在线调节和优化后，PID控制系统在蓄水水头高度为300 m时，控制效果，其通过控制后工程设备机组的转速超调量、转速上升耗时以及稳态误差三个指标数据体现，结果如图5所示。

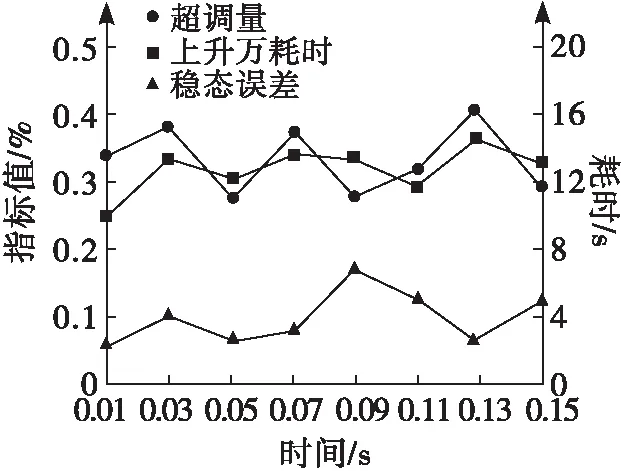
图5 优化前后的控制效果测试结果

依据图5结果可知：优化前PID控制系统控制后，工程设备机组的3项指标数据结果与优化后的指标数据结果存在明显差异，优化后的结果显著优于优化前的结果，其超调量均低于0.5%、转速上升耗时均在18 s以下，稳态误差低于0.2%。

为进一步衡量该文方法的控制效果，以工程设备的控制输出结果进行评价，获取在不同运行功率下，控制响应的输出结果(期望标准为在0.03 s内达到稳定状态)，测试结果如图6所示。

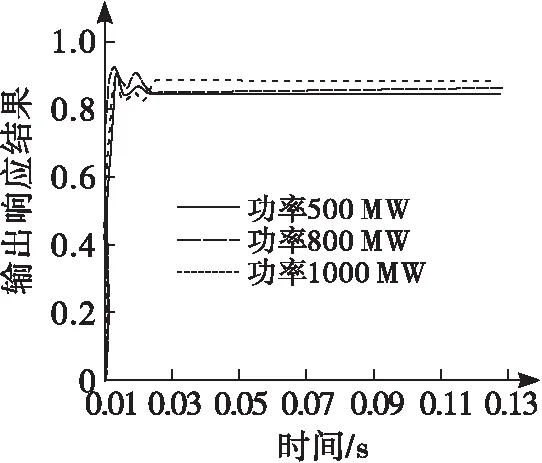
图6 控制响应的输出结果

依据图6结果可知：在不同功率下，该文方法应用后PID控制系统的控制响应结果均可在0.03 s完成输出响应，满足控制需求。该结果进一步体现该文方法的控制优越性以及应用性，能够最大程度提升PID控制系统的控制效果。

3 结论

水利枢纽工程中包含的工程类别较多，各个工程类别均通过不同的工程设备完成运行，该类设备在运行过程中，为保证水利枢纽的整体管理控制效果，通常采用PID控制系统完成。该文为提升水利枢纽工程设备的PID控制效果，研究基于半监督聚类算法的水利枢纽南工程设备自适应PID控制系统优化方法。经测试：该文方法能够实现PID控制系统相应参数的在线调节，并且聚类效果良好，可有效完成在线调节参数的聚类，完成最优参数获取，提升PID控制系统的控制效果，保证PID控制系统在水利枢纽工程设备控制过程中的稳定性。