结合电压谐波补偿和VSG的MMC-MG系统并离网切换控制
2022-08-12王兴贵董婉婉王海亮
王兴贵,董婉婉,王海亮
(兰州理工大学 电气工程与信息工程学院,甘肃 兰州 730050)
0 引言
传统交流微电网中微源通过桥式逆变器进行并网,不同微源逆变器之间并联,且每个逆变环节输出的电压幅值、相位、频率均不同,从而使系统内产生环流,降低系统电能质量[1-3]。为解决上述问题,文献[4]提出了一种模块化多电平串联结构微电网(Modular Multilevel Converter Microgrid, MMC-MG),该微电网具有输出电压正弦度高、频率稳定性好、输出功率等级易扩展等优点。
微电网具有孤岛和并网两种运行模式,当系统进行模式切换时,易发生大范围电压、频率波动现象,影响系统稳定运行。针对普通微电网的并离网切换,主要有双模式切换和单模式切换[5-6]。其中,虚拟同步发电机(Virtual Synchronous Generator, VSG)控制因具有电压源特性,能用于微电网并网运行和孤岛运行,因此,被广泛应用于微电网并离网切换领域。文献[7]在VSG的基础上,利用锁相环对公共耦合点(Point of Common Coupling, PCC)两端电压和相位进行预同步,减小模式切换时冲击电流的幅值。文献[8]在预同步环节中加入二次调压,不仅使系统在孤岛情况下稳定运行,且保证了系统并离网的平滑切换。文献[9]在PCC两端连接一个虚拟阻抗,通过控制虚拟阻抗上流过的虚拟无功功率或虚拟电流为零,保障系统运行模式平稳过渡。
该文在双闭环控制中加入电压谐波补偿,以降低系统孤岛转并网时发电模块电压波动对输出电压的影响。然后,引入VSG控制,该控制仅能保证系统并网转孤岛时稳定过渡,不能保证孤岛转并网时不产生冲击电流。因此,还需要加入预同步控制,缩小PCC两端电压幅值、相位的差值,确保系统模式切换过程的平滑过渡。
1 MMC-MG系统拓扑结构
MMC-MG系统拓扑结构如图1所示。该系统以MMC结构为基础,将光伏、风力微源经变换器后与混合储能系统(Hybrid Energy Storage System, ESS)并联,然后接入MMC半桥子模块电容两端,构成发电模块(Generation Module, GM)。每个桥臂均由N个GM和一个电抗器L构成。系统输出端经滤波装置给本地负载供电或将多余电能送入电网。
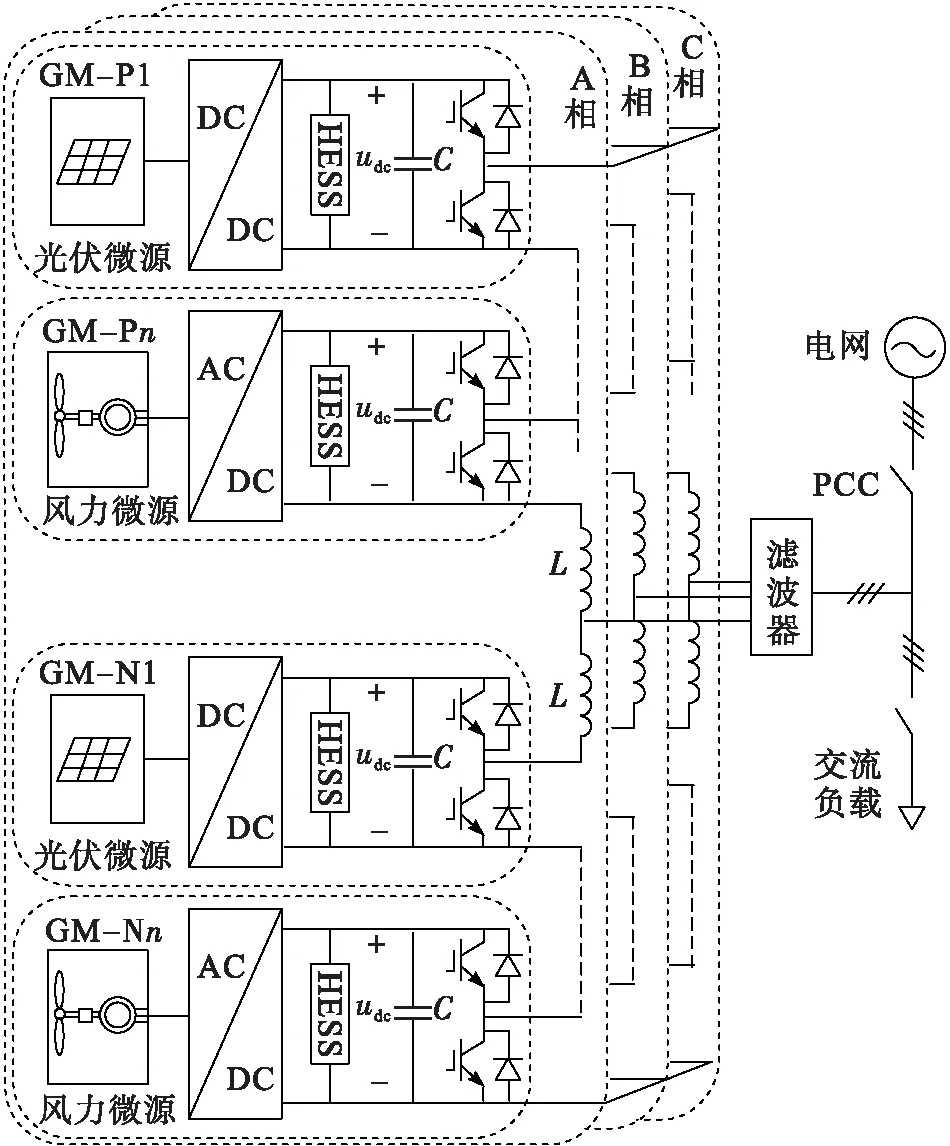
图1 MMC-MG系统拓扑结构
2 影响系统并离网切换的因素
2.1 GM输出电压波动
受桥臂电流交流分量的影响,混合储能控制下的GM输出电压仍存在较小波动。此时,载波移相调制(Carrier Phase Shifting SPWM, CPS-SPWM)下系统逆变环节输出电压Uab为[10]:
(1)
式中:uzab代表Uab中的直流分量;usab代表Uab中的基频偏差量;udc为GM电压;M为调制比;ω0为调制波角频率;N为投入GM个数。
其中,uzab、usab表达式如下:
(2)
(3)
式中:Δupj,Δunj(j=a,b,c)分别为上、下桥臂中GM电压偏差量。
从式(1)中看出,这些偏差量叠加会导致系统输出电压包含直流分量和基频偏差量。系统孤岛运行时,会使系统输出电压产生偏移;而系统孤岛转并网运行时,直流分量入网会降低并网电流质量。因此,需抑制系统所含的直流分量和基频偏差量。
2.2 系统离网转并网运行
图2是系统运行模式切换示意图。开关S断开时,系统处于孤岛运行,通过负载ZL的电流iL1为:
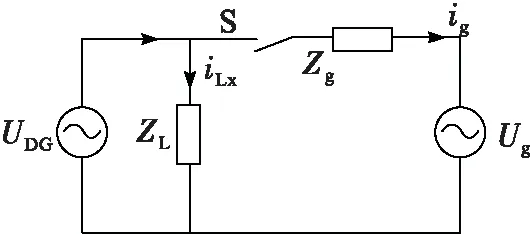
图2 系统运行模式切换示意图
(4)
式中:UDG,θDG,ωDG分别为逆变环节输出电压的幅值、相位和角频率。
开关S闭合时,系统处于并网运行,若忽略线路阻抗Zg,通过负载ZL的电流iL2为:
(5)
式中:Ug,θg,ωg分别为网侧输出电压幅值、相位和角频率。
式(4)(5)相减,可得电流差ΔiL:
(6)
(a)当UDG=Ug=U,ωDG=ωg=ω,θDG≠θg时:
(7)
(b)当UDG=Ug=U,ωDC≠ωg,θDG=θg=θ时:

(8)
(c)当UDG≠Ug,ωDG=ωg=ω,θDG=θg=θ时:
(9)
由式(7)~(9)可知,只有UDG=Ug,ωDG=ωg,θDG=θg时,ΔiL=0。若不满足上述要求,系统离网转并网会产生冲击电流。
3 系统孤岛转并网切换控制策略
VSG具有电压源特性,当系统由并网向孤岛转换时,系统输出电压幅值、相位、频率仅有微小变化,此时,直接断开PCC,系统仍可以稳定运行。因此该文主要研究孤岛转并网过程。
3.1 电压谐波补偿
2.1节中分析了GM输出电压波动对系统并离网切换的影响。假设A相上桥臂产生电压波动,令Δupa=m,其余值为零,对式(2)进行dq变换,可得:
(10)
对式(3)进行dq变换,可得:
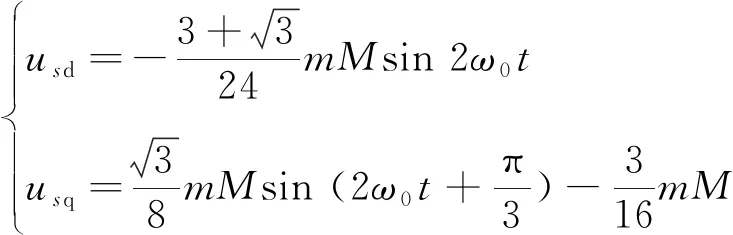
(11)
由式(10)、(11)可知,uzab,usab经dq变换后变为基频分量和二倍频分量,需要加入电压谐波补偿来降低GM电压波动对系统并离网切换的影响。其原理如图3所示。

图3 电压谐波补偿控制框图
系统输出电压Uabc经过Park变换后,通过低通滤波器得到直流分量,直流分量与原始值作差得到交流分量,再经PI调节后获得电压调节量,最后叠加到调制信号中,从而抑制直流分量。
3.2 VSG的基本原理及预同步控制
VSG的有功-频率环表达式如下[11]:
(12)
Pm=Pref+kω(ωn-ω)
(13)
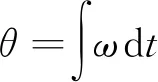
(14)
式中:J为转动惯量;Pm,Pe分别为VSG的机械功率、电磁功率;D为阻尼系数;ω为VSG输出的实际角频率;ωn为额定角频率;θ为参考电压相角;Pref为有功功率参考值;kω为调差系数。
VSG的无功-电压环控制方程为:
Uref=U0+kq(Qref-Q)
(15)
式中:Uref为VSG输出电压参考值;U0为额定电压;kq为无功调节系数;Qref,Q分别为无功功率参考值和实际值。
VSG控制输出的电压幅值与相位可近似看作MMC-MG系统的输出。在进行预同步时,采用VSG输出的电压幅值UVSG、相位θVSG与网侧Ug,θg进行比较,作相应的电压幅值和相位补偿。图4为VSG输出电压与网侧电压的矢量图。
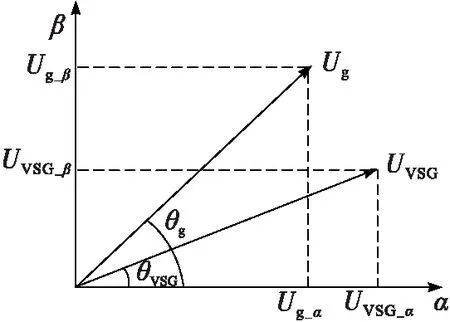
图4 VSG输出电压与网侧电压矢量图
将UVSG,Ug分解到αβ轴上,得电压差ΔU为:
(16)
将式(16)经PI调节送入VSG无功-电压控制环,用于补偿PCC两端电压幅值差,则式(15)变为:
(17)
式中:kpu,kiu分别PI控制器的比例、积分参数;
相位同步原理如下所示:
(18)
式中:ω*为补偿后的角频率;kpθ,kiθ分别为调节电压相位时PI控制器的比例、积分参数。
VSG一次调频属于有差调节。因此,借鉴电力系统二次调频原理,在原有的有功-频率环上引入积分补偿,可实现无差调节。此时,式(12)可变为:
(19)
式中:k为频率积分补偿系数。
要控制PCC自动闭合还需并网触发信号,该信号包含PCC两端相位差、电压差和频率差。当这三个条件同时满足阈值要求时,可触发PCC闭合。该文以sinΔθ作为相位触发信号,当Δθ足够小时,有sinΔθ≈Δθ,sinΔθ由图4计算可得:
(20)
PCC两端的电压差为:
|ΔU|=|UVSGsin(ωVSGt+θVSG)-Ugsin(ωgt+θg)|
(21)
若UVSG=Ug=U,ωVSG=ωg=ω,θVSG≠θg,则上式可化简为:
(22)
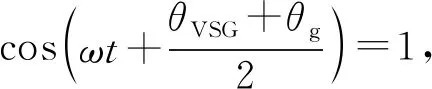
(23)
根据我国GB/T 33592-2017分布式电源并网运行规范控制规定[12],当Δf≤±0.2 Hz、Δθ≤15°、ΔU≤±5%UN时,系统可以并网。该文选取ΔU≤±3%UN、Δf≤±0.2 Hz时系统并网,此时,由式(23)计算出PCC两端相位差为1.72°。当Δθ=1.72°时,sin1.72°=0.03。图5是并网信号产生条件。图中,|u|表示对输入信号取绝对值,UN=220 V。

图5 并网信号产生条件
图6为包含电压幅值、相位、频率预同步的虚拟同步发电机控制策略。图7为MMC-MG系统并离网切换控制框图。系统孤岛运行时,仅需VSG控制、电压谐波补偿、双闭环控制及CPS-SPWM调制。系统孤岛转并网时,在上述控制的基础上,开启预同步控制。达到并网触发信号后,闭合PCC,同时退出预同步控制,系统处于并网状态。当接收到离网信号时,直接断开PCC即可。

图6 预同步与VSG结合控制策略示意图
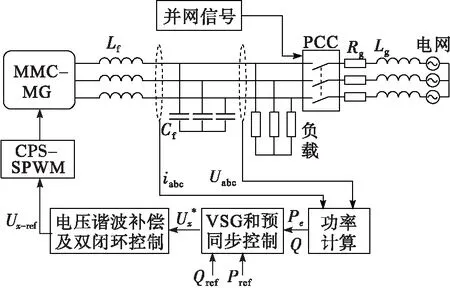
图7 MMC-MG系统并离网平滑切换控制框图
4 仿真分析
为验证该文所研究控制策略的有效性,搭建了MMC-MG系统并离网切换仿真模型,具体参数如表1所示。设置交流负载为阻性负载,有功功率为 5 kW,无功功率为0 Var。VSG中Pref=10 kW,Qref=0 Var。初始时刻,系统处于孤岛运行模式,0.4 s接收到并网信号,1.5 s系统由并网转孤岛运行。
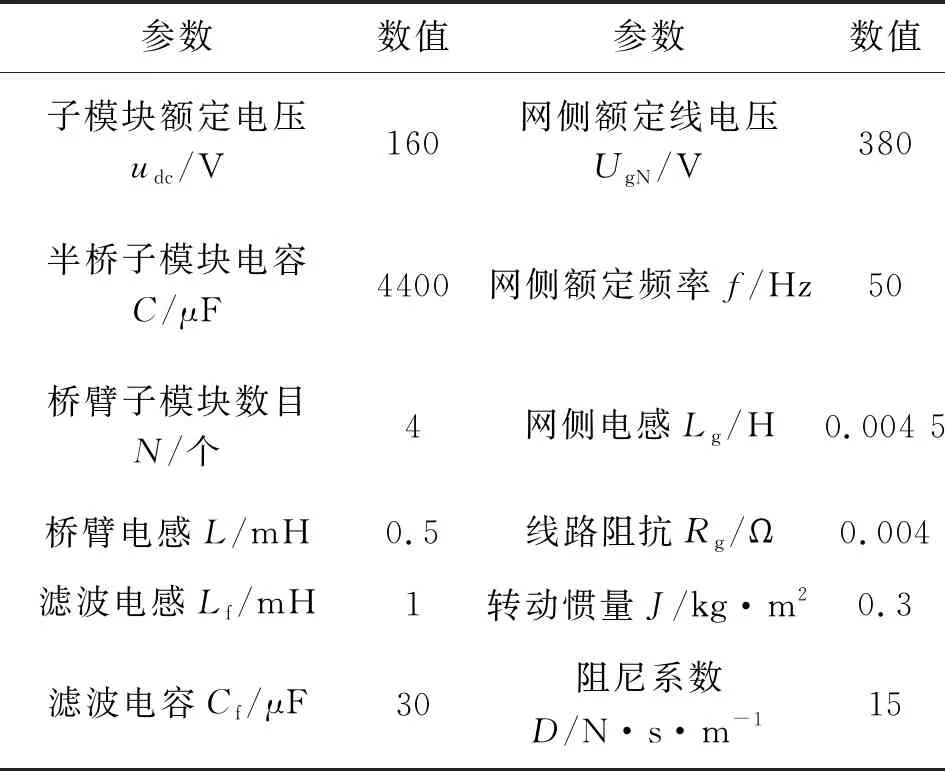
表1 系统仿真模型参数
4.1 电压谐波补偿
设置系统A相上桥臂upa1=140 V,B相上桥臂upb2=170 V,其余每个GM电压均维持160 V。图8是加入电压谐波补偿前后系统并离网切换输出电压、电流的对比仿真图。

图8 电压谐波补偿波形图
4.2 MMC-MG系统孤岛转并网运行
图9为系统孤岛转并网输出电压波形。未加预同步控制时,系统输出电压从311 V跌落至270 V。加入预同步后,系统并网时电压跌落现象得到缓解,电压可维持在311 V左右,较为稳定。
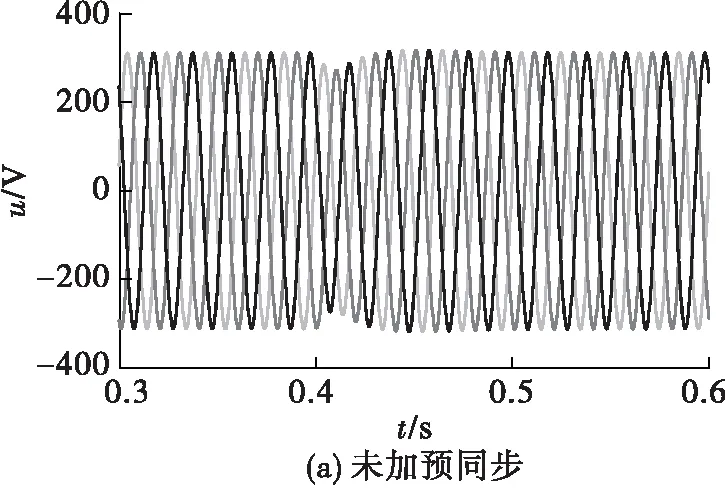
图9 系统孤岛转并网输出电压波形
系统孤岛转并网逆变侧输出电流波形如图10所示。未加入预同步时,并网瞬间产生幅值高达100 A的冲击电流。闭合预同步开关S1-S2后,系统并网未产生冲击电流,可实现平滑过渡,但过渡时间较长,大约需要0.38 s。在此基础上,加入二次调频,即闭合开关S3,预同步时间缩短了0.1 s。

图10 系统逆变侧输出电流波形
图11为系统孤岛转并网时网侧输出电流波形。可以看出未加预同步控制时,入网电流产生冲击,幅值约为98 A。加入预同步后入网电流没有出现冲击,0.1 s后电流幅值稳定在11 A。
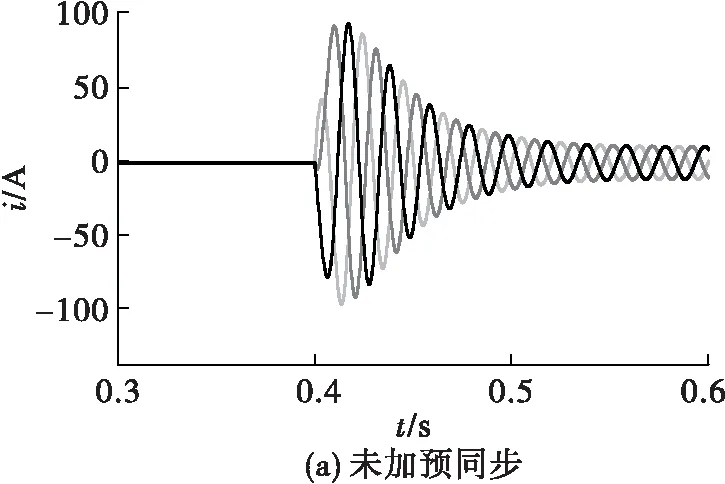
图11 网侧输出电流波形
4.3 MMC-MG系统并网转孤岛运行
系统由并网转孤岛运行仿真波形如图12所示。1.5 s系统并网转孤岛运行时,电压有一瞬间的冲击,幅值约为324 V,其波动未超过5%,符合电压稳定性判定标准。且电流在切换瞬间未发生明显畸变。

图12 系统并网转孤岛仿真分析
5 总结
该文针对发电模块电压存在波动,从而导致系统并离网切换时输出电压不稳定的问题,提出了一种电压谐波补偿和二次调频预同步相结合的MMC-MG系统并离网平滑切换控制策略。仿真结果表明,所提控制策略不仅可以缓解系统电压偏移现象,还可以在模式切换时减小冲击电流、降低频率波动、缩短预同步并网时间、保证系统安全可靠运行。
