迭代法解线性方程组的并行算法设计与实现
2022-08-12郭警涛
姬 进,艾 莉,郭警涛,赵 君,闫 稳
(航空工业西安航空计算技术研究所,陕西 西安 710065)
并行计算机不仅仅是一种获得高性能的手段,它同时也具有将计算能力从单个处理器无缝地扩展到无限多个处理器的潜力。这种潜力在几十年前就已被人们所熟知,但是直到20世纪80年代末,它才真正显现出来。
本文先对并行计算的一些基本概念作个简单介绍,然后介绍线性方程组的两种迭代法的并行算法的原理和实现,最后对这两种算法作出相应的测试和性能分析。
1 线性方程组的并行计算简述
并行计算就是在并行计算机上,将一个应用分解成多个子任务,分配给不同的处理器,各个处理器之间相互协同,并行地执行子任务,从而达到加快求解速度,或者提高求解应用问题规模的目的[1-2]。
线性方程组是指矩阵含有大量零元素的线性代数方程组。矩阵多种多样,主要可以分为具有规则结构的结构和无规则结构的矩阵基本类型。
求解线性方程组的算法中,有两类最基本的算法,一类是直接法,即以消去为基础的解法,如果不考虑误差的影响,从理论上讲,它可以在固定步数内求得方程组的准确解;另一类是迭代解法,它是一个逐步迭代求得近似解的过程,这种方法便于编制程序,但存在着迭代是否收敛及收敛速度快慢的问题;在迭代过程中,由于极限过程一般不可能进行到底,因此只能得到满足一定精度要求的近似解。
2 迭代法介绍
在科学工程领域中,经常需要求解形如Ax=b的线性方程组,其中A为n×m的矩阵,称为系数矩阵;b为n维向量,称为列向量;x为待求解的m维列向量,常简称解向量。在本论文中仅考虑m=n的情形。
迭代法的一般形式化可以描述为:
x(k)=φk(x(k-1),…,x(k-l)),k=l,l+1,…, .
(1)
其中φk称为迭代算子,x(0),x(1),…,x(l-1)称为初值。通常称上式为l步迭代法,当l=1时称为单步迭代法。如果算子φk与k无关,则称为定常迭代,否则为非定常迭代。如果φk为线性算子,则称为线性迭代,否则为非线性迭代。
在求解线性方程组的迭代法中,单步定常线性迭代扮演着重要的角色,该迭代可以描述为:
x(k)Gx(k-1)+c,k=1,2,3,…,.
(2)
其中x(k)与c为n维向量,G为n阶矩阵。如果存在x,使得对任意初值x(0),由上式产生的序列{x(k)}都收敛于x,则称该迭代法收敛,且记1imx(k)=x,否则发散。
3 迭代法并行算法设计
3.1 雅克比迭代法
对于方程组Ax=b,记D,-L,-U分别是A的对角、严格下三角、严格上三角部分构成的矩阵,即A=D-L-U。这时方程组(1)式可以变成:
Dx=b+(L+U)x.
(3)
如果方程组右边的x已知,由于D是对角矩阵,可以很容易求得左边的x,这就是雅克比(Jacobi)迭代的出发点。因此,对于给定的初值x(0),雅克比迭代法如下:
x(k)=D-1(L+U)x(k-1)+D-1b.
(4)
记G=D-1(L+U)=I-D-1A,c=D-1b.
对于方程组Ax=b式,方程组的每个方程ailx1+ai2x2+…+ainxn=bi可以很容易地写成如下的形式:
(5)
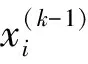
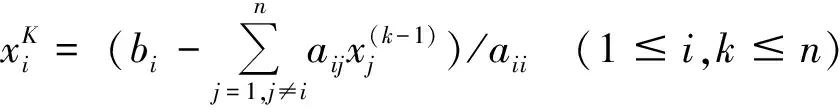
(6)

设有p个处理器,则将矩阵划分为p块,每块含有连续的m行向量,这里m=[n/p],编号为i的处理器含有A的第im至第(i+1)m-1行数据,同时向量b中下标为im至(i+1)m-1的元素也被分配至编号为i的处理器(i=0,1,…,p-1),初始解向量被广播给所有的处理器。
在迭代计算中,各处理器并行计算解向量x的各分向量值,编号i的处理器计算分量xim至x(i+1)m-1的新值。并求其分量中前后两次值的最大差localmax,然后通过归约操作的求最大值运算,求得整个n维解向量中前后两次值的最大差值max,并广播给所有的处理器。最后通过扩展收集操作将各处理器中的解向量按处理器编号连接起来,并广播给所有的处理器,以进行下一次迭代计算,直至收敛。具体算法描述见算法1。
算法1 线性方程组的雅克比迭代并行算法
max=ε+1;
While max>ε do
Fori=0 tom-1 do
sum=0.0;
Forj=0 ton-1 do
Ifj≠myid×m+ithen
sum=sum+aijxi;
End if
End for
End for
Fori=1 tom-1 do
End if
End for
将x的所有分量的新值广播到所有处理器;
求出所有处理器中localmax值的最大值max,
并广播给所有的处理器中;
End while
3.2 高斯-赛德尔迭代法
在并行计算中采用与雅克比迭代类似的数据划分。对于高斯-赛德尔迭代,计算xi的新值时,使用xi+1,…,xn-1的旧值和x0,…,xi-1的新值。计算过程中xi与x0,…,xi-1及xi+1,…,xn-1的新值会在不同的处理器中产生,因此可以考虑采用时间偏移的方法,使各个处理器对新值计算的开始和结束时间产生一定的偏差。编号为myid的处理器一旦计算出xi(myid×m≤i≤(myid+1)×m)的新值,就立即广播给其余处理器,以供各处理器对x的其他分量计算有关xi的乘积项并求和。当它计算完x的所有分量后,它还要接收其他处理器发送的新的x分量,并对这些分量进行求和计算,为计算下一轮的xi作准备。计算开始时,所有处理器并行地对主对角元素右边的数据项进行求和,此时编号为0的处理器(简称为P0)计算出x0,然后广播给其余处理器,其余所有的处理器用x0的新值和其对应项进行求和计算,接着P0计算出x1,x2,…,当P0完成对xm-1的计算和广播后,P1计算出xm,并广播给其余处理器,其余所有的处理器用xm的新值求其对应项的乘积并作求和计算。然后P1计算出xm+1,xm+2,…,当P1完成对x2×m-1的计算和广播后,P2计算出x2×m…,如此重复下去,直至xn-1在PP-1中被计算出并广播至其余的处理器之后,P0计算出下一轮新的x0,这样逐次迭代下去,直至收敛为止。具体算法描述见算法2。
算法2 高斯-赛德尔迭代并行算法
Fori=myid×mto (myid+1)×m-1 do
sumi=0.0;
Forj=i+1 ton-1 do
sumi=sumi+aijxi;
End for
End for
total=0;
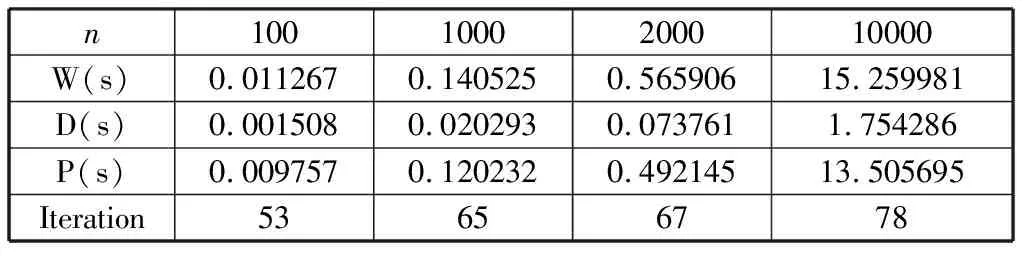
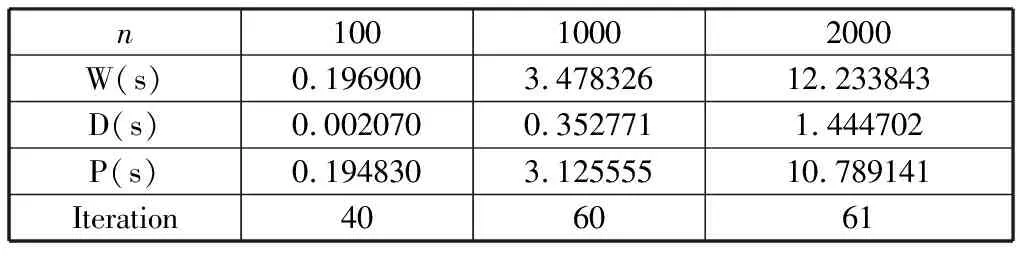
Whiletotal iteration=0; Forj=0 ton-1 do q=j/m; Ifmyid==qthen temp=xj,xj=(bi-sumi)/aii; If |xi-temp|<ε then iteration=iteration+1; End if 将xj的新值广播到其他所有处理器; sumi=0; Fori=myid×mto (myid+1)×m-1 do Ifj≠ithen sumi=sumi+aijxi; End if End for Else 接受广播来的xj的新值; Fori=myid×mto (myid+1)×m-1 do sumi=sumi+aijxi; End for End if End for 求出所有处理器中iteration值的和total并广播到所有处理器; End while 假设某个串行应用程序在某台并行计算机上单处理器上的执行时间为Ts,而该程序并行化后,P个进程在P个处理器并行执行所需要的时间为Tp,则该并行程序在该计算机上的加速比可定义为: (7) 效率定义为: (8) 加速比和效率是衡量一个并行程序性能的最基本评价方法,显然执行最慢的进程将决定并行程序的性能。 该算法的时间复杂度为O(mm),其中m为每个进程中矩阵的行数。在单进程计算时,m=n,此时的时间复杂度为O(n2),从表1中可以看到执行时间随着规模的增大也相应增大了n2倍。 表1 单进程雅克比迭代并行算法运行时间 当求解规模在10000时,其对应的单进程执行时间为72.340110 s,两个进程并行执行时间为25.584798 s,可以求得其加速比S2=2.82,效率E2=1.41,四个进程并行执行时间为13.505695 s,易求得加速比S4=5.50,效率E4=1.375。两个或四个进程并行后,迭代次数减少了(从表2和表3中可以看到),所以其并行后计算时间明显减少,从而导致加速比明显增大,也导致该并行算法的效率很高。 表2 两个进程雅克比迭代并行算法运行时间 表3 四个进程雅克比迭代并行算法运行时间 通过表4和表5可看到:高斯-赛德尔迭代的并行性较差,当增加进程数量时,时间并没有减少,这是由于高斯-赛德尔迭代每次要用前面计算的新值,因此算法会有一定的等待时间,导致整体性能下降。 表4 两进程高斯-赛德尔迭代并行计算运行时间 表5 四进程高斯-赛德尔迭代并行计算运行时间 线性方程组的迭代求解是一种逐步求得近似解的过程,这种方法的好处是方法简单,便于编制程序,但是迭代法必须符合合适的迭代格式及初始向量,以使得迭代过程尽快收敛。本文介绍了两种经典的迭代算法——雅克比迭代和高斯-赛德尔迭代,并设计了其并行算法。雅克比迭代有着内在的并行性,因此它的并行性较高斯-赛德尔迭代较好,但是高斯-赛德尔迭代要利用上次最新的值,因此在并行性上有所欠缺,但是它的收敛速度却提高了。4 算法测试与性能分析
4.1 雅克比迭代法性能分析
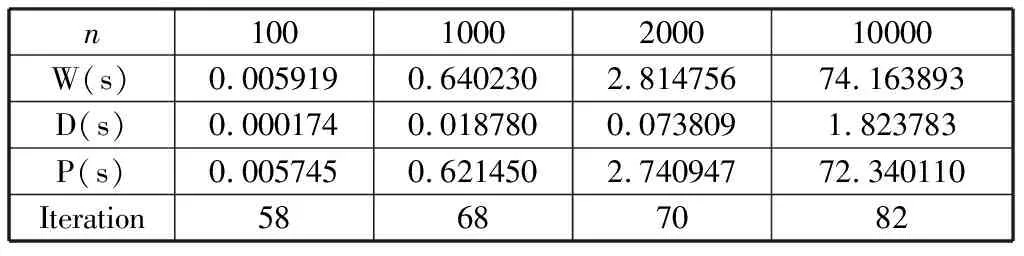
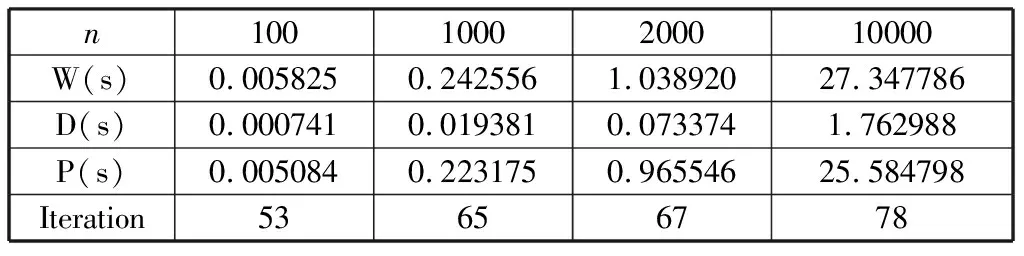
4.2 高斯-赛德尔迭代性能分析

5 结束语
