基于线性谱聚类超像素分割和联合稀疏表示的高光谱图像分类算法
2022-08-12魏宏超王永丽丁晓云陶菊亮
魏宏超,王永丽,丁晓云,陶菊亮
(山东科技大学 数学与系统科学学院,山东 青岛 266590)
随着遥感传感器技术的不断发展,高光谱图像(hyperspectral image,HSI)以精细的光谱分辨率得到越来越广泛的应用[1],例如环境监测[2]、矿物勘探与分析[3]、城市发展分析[4-5]等等。HSI在各大领域的广泛应用,使得图像分析处理也变得越来越重要。
分类作为高光谱图像分析处理的重要手段之一,其目标是对每一个像素进行准确的类标识。目前,高光谱图像分类主要分为有监督分类、半监督分类和无监督分类三种。稀疏表示(sparse representation,SR)算法[6]作为有监督分类的一种,以其较好的分类效果在高光谱图像分类中得到广泛应用[7]。考虑到在同一类别的像素应具有相似的光谱特征,SR算法采用属于同一类别的少量训练样本线性表示每一个待分类的测试样本,计算对应的稀疏系数,然后求解两者的最小残差,并以此确定所属类别。
传统的SR算法只考虑HSI的基本光谱信息,忽略了像素间的空间邻域信息,容易导致高光谱图像分类结果不平滑[8]。为了克服这个问题,一些学者引入HSI在空间分布上的一致特性,提出将光谱信息和空间信息相融合的分类算法。Chen等[9]利用相同训练样本表示领域内的所有像素,充分考虑像素间的空间邻域信息,提出联合稀疏表示(joint sparse representation,JSR)算法;Fang等[10]在多尺度空间上,通过自适应的稀疏矩阵实现对HSI的精准分类。然而,通常情况下,HSI地物种类非常复杂,不同种类间不一定完全排斥,导致其空间分布的一致性并非普遍存在。同时,高光谱图像的像素间还普遍存在同类异谱和异类同谱的现象,导致分类精度降低。
同时,诸如SR这类监督分类算法通常需要大量的训练样本,而在实际应用中获取大量的训练样本费时费力,不容易实现,影响分类精度。针对这一问题,一些学者提出无监督分类算法,该类算法的最大优点是不需要高光谱图像的先验信息,例如K-means算法[11]、均值漂移(mean-shift)算法[12]和基于密度的带噪声的空间聚类方法(density-based spatial clustering of applications with noise,DBSCAN)[13]等。相对于监督分类必须以图像存在样本标签为前提,非监督分类的分类效率比较高效,但主要缺陷是精度不高,对于参数的敏感度极高,聚类效果的稳定性也很差,并且随着高光谱图像维度的增加分类效率会下降。
针对以上问题,本研究在文献[14]的基础上提出一种基于线性谱聚类(linear spectral clustering,LSC)超像素和谱聚类相融合的相关系数联合稀疏表示算法。该算法通过LSC超像素分割从全局上考虑高光谱图像的数据特征,在利用高光谱图像的光谱信息和空间信息的同时,充分考虑噪声及区域边界对分类效果的影响,克服了由于同类异谱和异类同谱现象导致的分类精度较低的问题,减少了类间干扰。图1为算法执行过程,是基于LSC超像素分割、谱聚类和联合稀疏表示的高光谱图像三级分类算法。首先,通过主成分分析(principal component analysis,PCA)降维实现对高光谱图像的LSC超像素分割,从分割后的超像素块中选取一小部分作为标签样本进行类别标注,并将剩余的超像素块作为训练样本;其次,通过K-means和谱聚类算法将训练样本分成两类,按规则选取其中一类作为测试样本,并计算测试样本与标签样本之间的相关系数;然后,对选出的测试样本进行稀疏矩阵计算,进而计算出测试样本与各类标签样本的最小残差,并将其作为所有训练样本的最小残差;最后,用基于表示残差和相关系数的决策函数对像素进行分类。
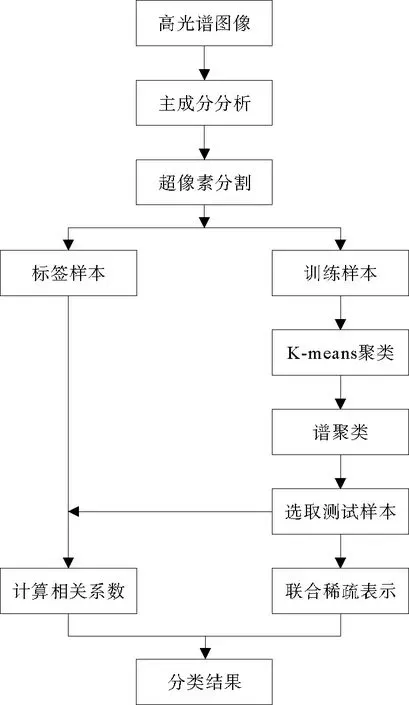
图1 算法执行过程
1 相关工作
1.1 超像素分割技术
超像素分割是2013年提出的图像分割技术[15],是将图像细分割成若干统一、均匀、互不重叠的子区域,每个区域包含了一定的纹理、颜色和亮度等物理特征[16]。超像素分割利用像素之间特征的相似性,将像素进行分组并捕获图像的冗余信息,大大降低了后续图像处理任务的复杂度。分割的超像素块数越多,图像超像素分割越细,则每个超像素包含的像素越少;反之,每个超像素包含的像素越多。图2展示了对同一幅图像进行不同分割数量的超像素分割结果。
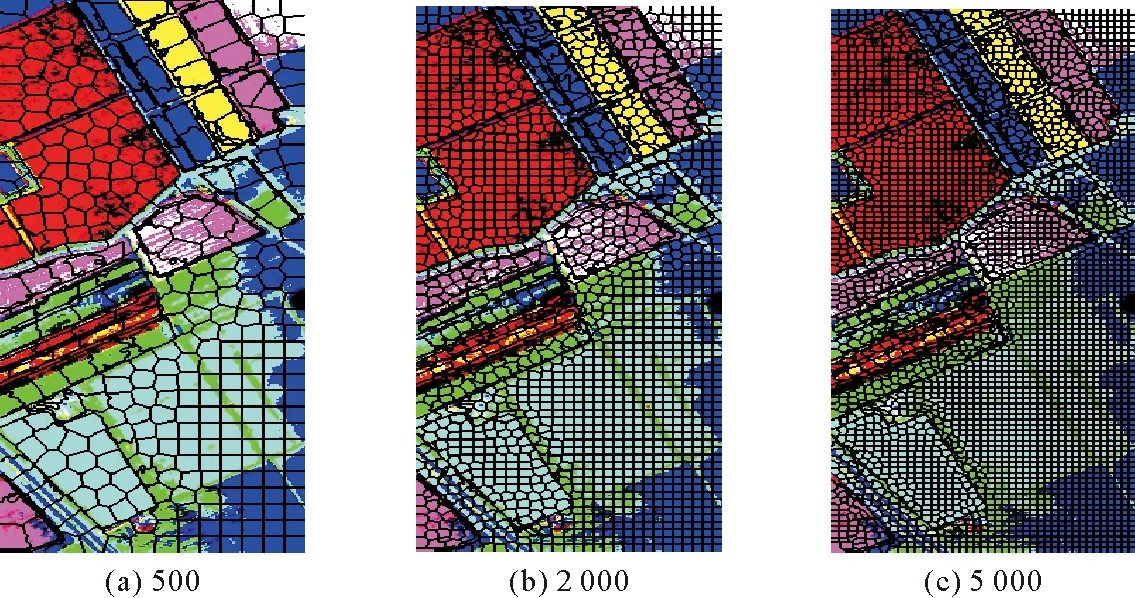
图2 不同数量超像素分割结果
由于超像素所具备的这种同质特性,引起高光谱图像分类研究者们的极大兴趣。Fan等[17]将超像素分割集成到低秩表示中,提出一种新的去噪方法SS-LRR。Zhang等[18]为了克服利用结构信息的缺点,提出一种基于多尺度超像素的稀疏表示算法用于高光谱图像分类。Zu等[19]提出一种基于简单线性迭代聚类(simple linear iterative clustering,SLIC)超像素分割技术的l2,1范数鲁棒主成分分析HSI分类算法。相关实验结果表明,应用超像素分割技术进行HSI分类,不仅能解决HSI降维的问题,而且借助超像素的局部性质,可以为HSI分析提供丰富的空域结构信息。
目前,超像素分割技术主要有LSC[20]、Normalized cuts[21]、Mean shift[22]、Turbo-pixel[23]、SLIC[24]等。其中,SLIC作为一种基于局部特征的算法,以思想简单和分割快速的优点被广泛使用,但因其无法与全局优化信息进行有效地结合,影响了超像素分割的效果,导致超像素的边界依附性和形状紧凑性不理想。而LSC作为一种基于归一化割集的图像分割方法,利用两种看似不同方法之间的数学等价性将像素数据显式地映射到高维特征空间,通过桥接局部和全局的方法,有效地解决了高复杂度的全局问题[20]。与SLIC相比,LSC不仅生成的超像素能很好地适应自然图像的纹理和结构,而且还可以捕获全局信息,具有良好的形状紧凑性和边界附着力。
1.2 谱聚类算法
谱聚类[25]是一种基于图的聚类方法,其分类思想是找到数据集中类内相似度最大而类间相似度最小的划分。谱聚类算法可以对任意形状的数据进行最优划分,然而由于计算图划分准则的最优解是一个不确定性多项式难问题,所以对此类问题的求解通常是转化为求解相似度矩阵的谱分解问题,利用谱分解得到合适的特征向量来描述数据的低维结构,并在低维空间中利用K-means等经典方法得到最终的聚类结果。
谱聚类算法基本思想是,首先构建样本集的相似度矩阵W,然后通过计算W的前K个特征值与特征向量,构建特征向量空间,最后利用K-means或其他经典聚类算法对特征向量空间中的特征向量进行聚类。
由于谱聚类算法涉及降维处理,相比传统聚类算法,谱聚类算法对高维度数据的聚类效果会更加突出。同时,谱聚类算法不需要样本服从某种分布,在很大程度上避免了样本空间分布假设的局限性,能够聚类成任何样本形状。
1.3 联合稀疏表示分类算法
联合稀疏表示分类算法[26]是在假设相邻的高光谱图像通常由相似的物质组成,从而具有相同光谱特征的前提下提出来的,具体表述如下。
给定N个训练样本,设地物类别数为M,并记S={1,2,…,N},S=S1+S2+…+SM。其中,Sm为第m类训练样本(m=1,2,…,M)。设第i个训练样本的光谱向量为xi(i∈S),其字典矩阵为X=(x1,x2,…,xN),设y={y1,y2…,yt}为当前待分类像素邻域矩阵(t为邻域内像素总数),则关于y的联合稀疏表示为:
(1)
式中:α=[α1,α2,…,αt],αj(j=1,2,…,t)为第j个像素的稀疏系数向量,可由α中非零元素对应的字典类型判别y在X中的归属;‖·‖F为F范数;‖α‖row,0是稀疏矩阵中非零行的个数,η为给定的稀疏水平。
对于式(1),采用同步正交匹配追踪(simultanaous orthogonal matching pursuit,SOMP)算法[27]进行求解,得到稀疏矩阵α,并以此计算y被第j类字典表示的残差
rj(y)=‖y-Xj·αj‖F。
(2)
式中:j=1,2,…,M;Xj和αj分别为X和α的第j列和第j行。则基于残差的像素分类可以描述为:
(3)
1.4 相关系数
相关关系是一种非确定的关系,相关系数是研究两变量间线性相关程度的有效度量。对于高光谱图像而言,每一个像素都有n维谱段组,本研究利用简单相关系数来计算HSI两个像素间的相关性:
(4)
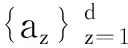
2 算法提出
2.1 LSC算法
LSC算法是在研究归一化割集的目标函数和加权K-means关系的基础上提出来的,是一个以五维(L,a,b,x,y)空间为基础进行分割的超像素分割算法,其中(L,a,b)为彩色图像转化为CIELab颜色空间后的三维向量,(x,y)为像素坐标位置。而对高光谱图像G∈RM×N×H,其(M,N)为像素坐标位置,H为波段数(H>3)。因此,需要对H个波段进行降维后才能用LSC算法对高光谱图像进行超像素分割。采用PCA算法对高光谱图像进行数据预处理,选取前3个主成分作为超像素分割的数据。
但该算法并不是在五维特征向量空间中完成的,而是利用了两种看似不同的方法之间的数学等价性,将数据点映射到高维特征空间中以提高线性可分性。算法1给出了LSC超像素分割算法的实现步骤。其中,Vx/Vy近似等于图像的纵横比,t≥0.5是平衡局部紧致性和全局最优性的一个参数。在聚类合并阶段,根据经验,将小于预期超像素大小1/4的孤立小像素点与相邻的大像素点合并。

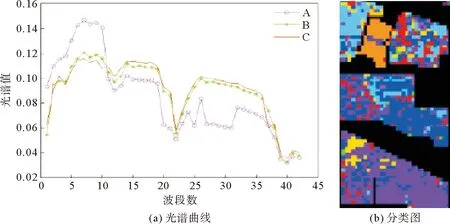
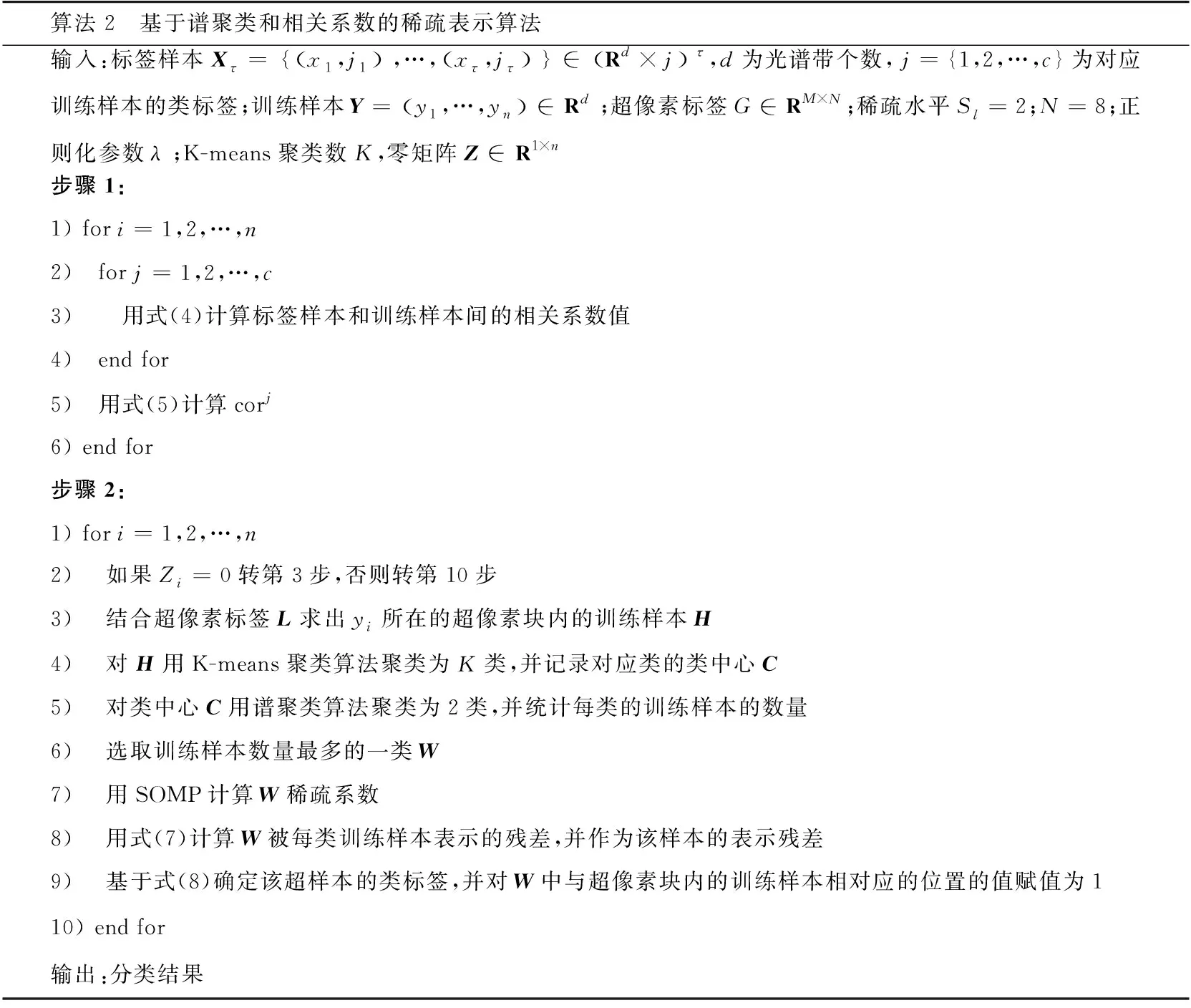
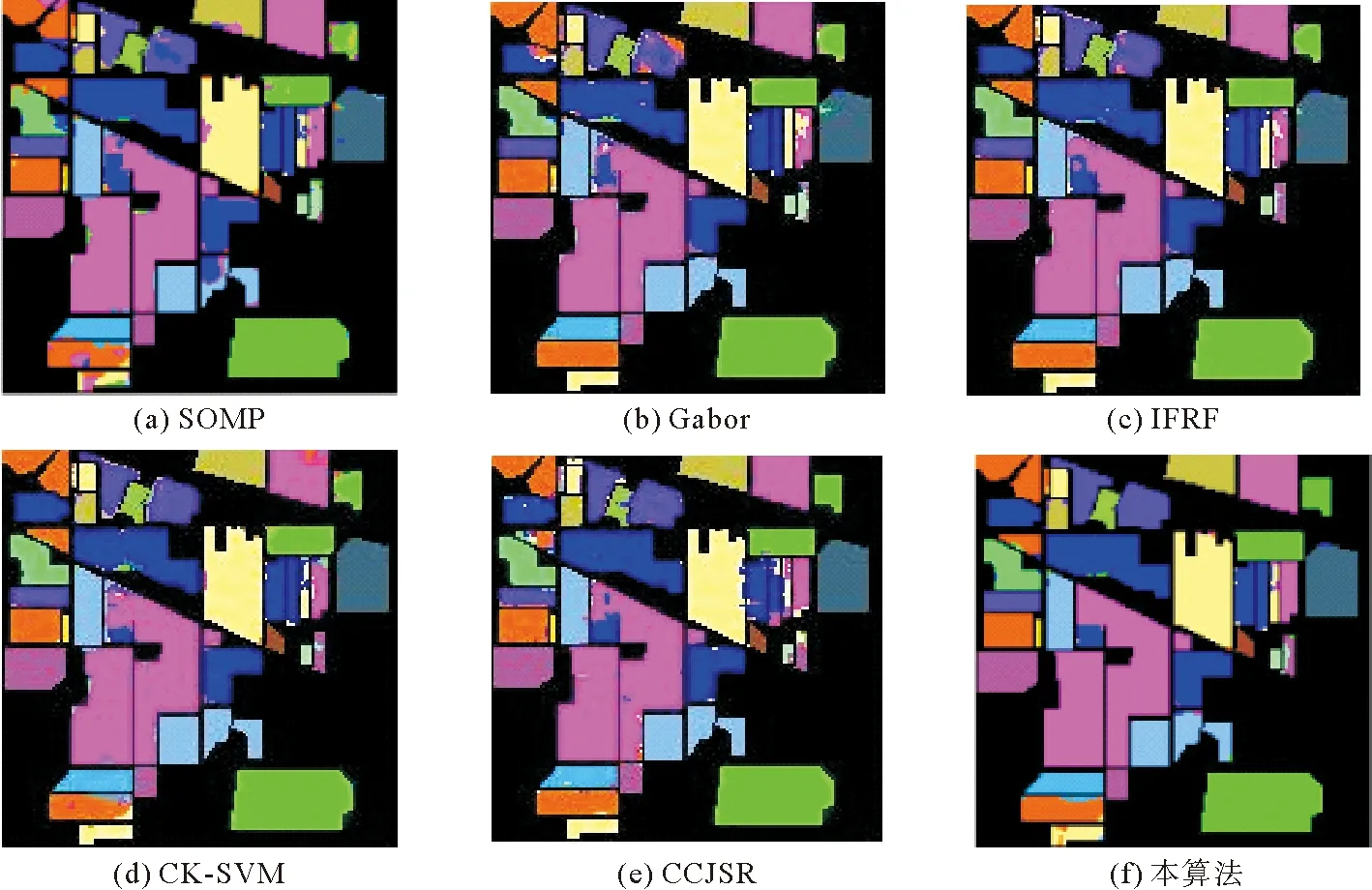
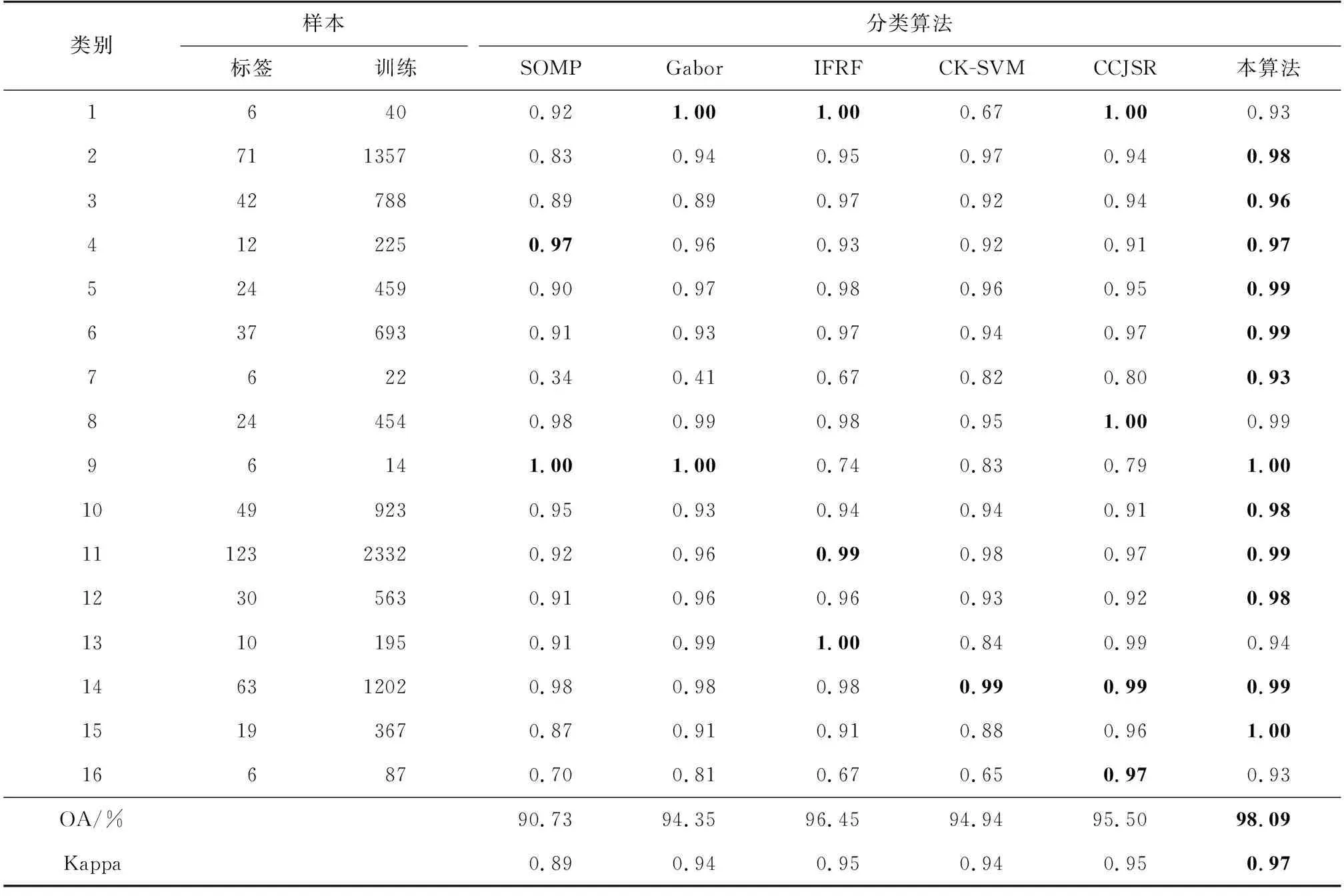
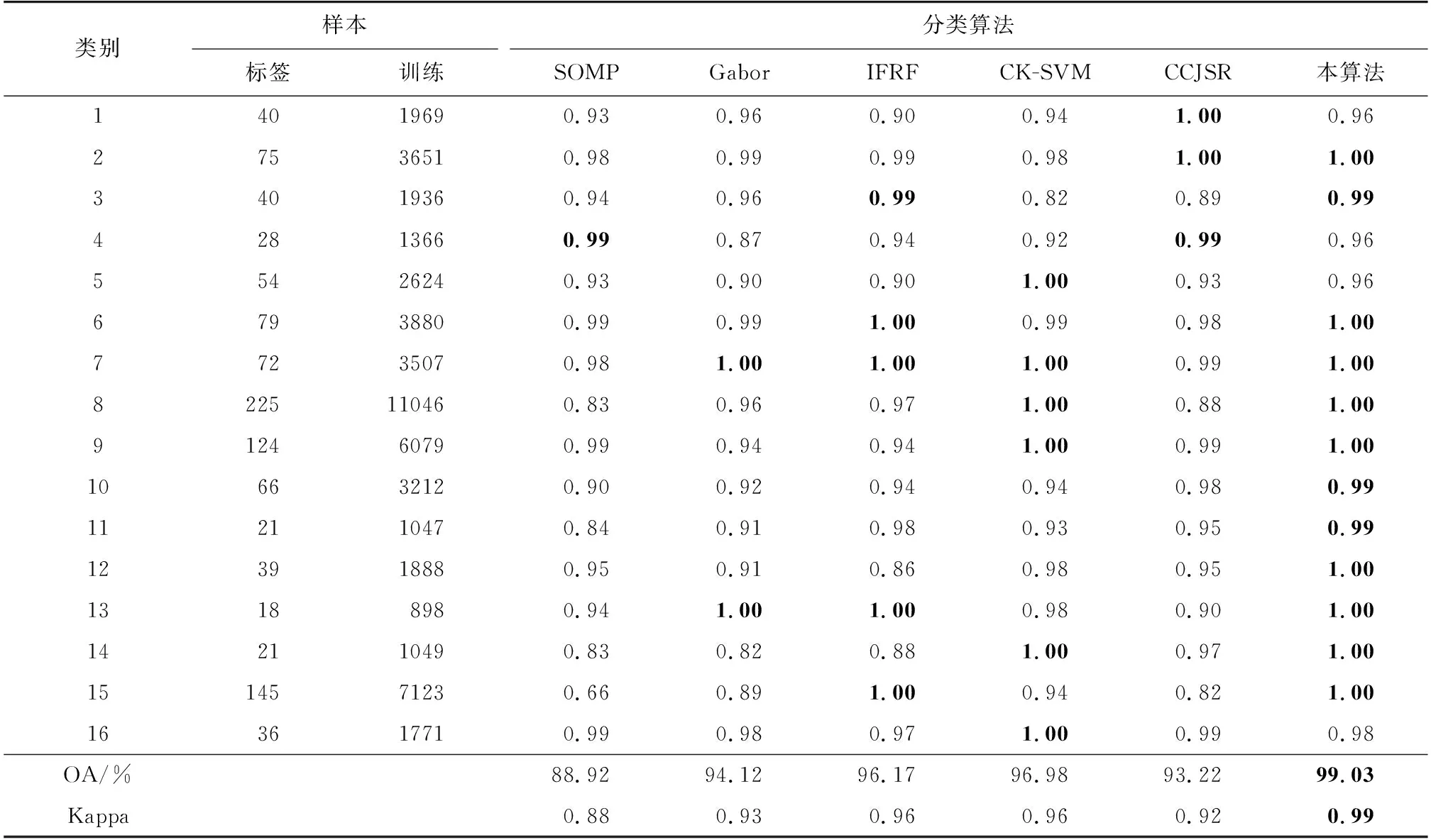
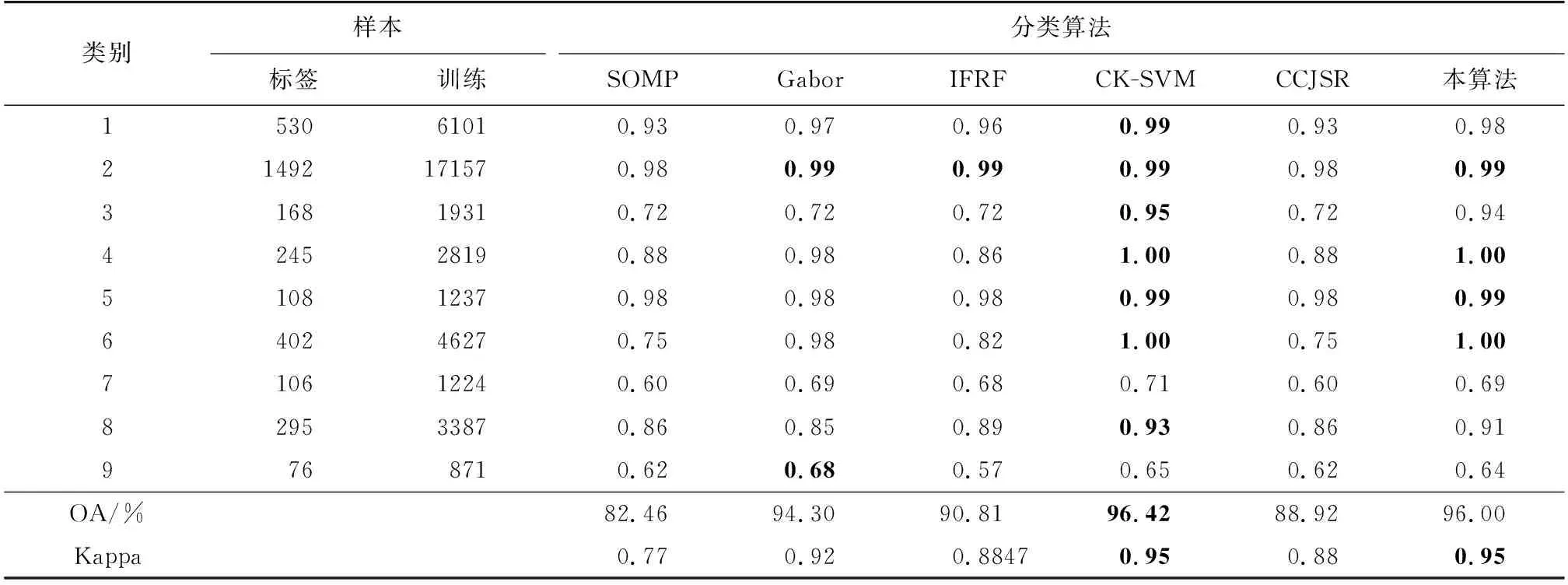
算法1 LSC超像素分割算法输入: PCA预处理后的高光谱图像数据,t=0.5,超像素数k初始化:1) 将每个五维像素点p映射到高维特征空间中的一个向量ϕ(p)2) 以固定的水平间隔Vx和垂直间隔Vy在图像上均匀采样k个种子点3) 通过种子点初始化相应簇的加权平均值mk和搜索中心ck4) 对每个像素点p设定标签L(p)=0,设定距离D(p)=∞迭代:1) for 每个加权平均值mk和搜索中心ck do2) for 搜索中心ck的tVx*tVy领域中的像素点p do3) 计算ϕ(p)和mk之间的欧氏距离d4) if D 2.2.1 算法分析 经LSC超像素分割后的每一块超像素都是在空间分布上具有一致性的区域。但如图3所示,在高光谱图像中同类异谱和异类同谱现象普遍存在且无法避免。图3(a)光谱曲线图中的曲线A和B所对应的光谱曲线存在很大的差异,但两者却为同一类别,即同类异谱现象;而曲线A和B所对应的光谱曲线趋势十分相近,但两者却为不同类别,即异类同谱现象。当超像素块分的较细,而超像素块中又存在严重的同类异谱现象时,会导致分类结果错分严重,如图3(b)。反之,当超像素块分的较少时,每个像素块包含的像素数就会较多,而谱聚类构造相似矩阵和进行特征值分解的时间复杂度通常随着像素数量的增多而增加,导致计算复杂度增加。 图3 光谱曲线图和分类图 针对第一个问题,采取“少数服从多数”的选取规则,即将像素通过谱聚类分为两类后,分别统计两个类别的像素个数,选取个数多的一类作为联合稀疏表示的待分类测试样本集。针对第二个时间复杂度的问题,在谱聚类之前对待分类训练样本集进行一次K-means粗分类,得到相对应类别数的聚类中心,然后再对其进行谱聚类处理,这样在不损害聚类精度的同时大大降低了谱聚类的时间复杂度。同时当超像素块内任意一个训练样本得到分类标签后,对超像素块内其余测试像素赋值相同的类标签,并对该部分训练样本进行标记剔除,使其不参与循环,通过这种策略,可以极大降低算法的时间复杂度。 2.2.2 算法实现 提出一种结合谱聚类、相关系数和联合稀疏表示的高光谱图像分类算法,算法2展示了该分类算法的执行过程。具体求解过程如下。 首先,为了提高噪声点和边界处的分类效果,利用式(4)对标签样本和训练样本间的相关系数进行计算,即 (5) (6) 根据式(1),可得稀疏矩阵 (7) 于是,每类样本的残差为: (8) 式中:j=1,2,…,c;c为样本类别。 最后,根据决策函数确定每个样本的类标签。通过在决策函数中引入正则化参数λ,实现联合稀疏表示和相关系数之间的平衡,得到训练样本y的最终类标签 (9) 算法2 基于谱聚类和相关系数的稀疏表示算法输入:标签样本Xτ=x1,j1 ,…,xτ,jτ ∈Rd×j τ,d为光谱带个数,j={1,2,…,c}为对应训练样本的类标签;训练样本Y=y1,…,yn ∈Rd;超像素标签G∈RM×N;稀疏水平Sl=2;N=8;正则化参数λ;K-means聚类数K,零矩阵Z∈R1×n步骤1:1) for i=1,2,…,n2) for j=1,2,…,c3) 用式(4)计算标签样本和训练样本间的相关系数值4) end for5) 用式(5)计算corj6) end for步骤2:1) for i=1,2,…,n2) 如果Zi=0转第3步,否则转第10步3) 结合超像素标签L求出yi所在的超像素块内的训练样本H4) 对H用K-means聚类算法聚类为K类,并记录对应类的类中心C5) 对类中心C用谱聚类算法聚类为2类,并统计每类的训练样本的数量6) 选取训练样本数量最多的一类W7) 用SOMP计算W稀疏系数8) 用式(7)计算W被每类训练样本表示的残差,并作为该样本的表示残差9) 基于式(8)确定该超样本的类标签,并对W中与超像素块内的训练样本相对应的位置的值赋值为110) end for输出:分类结果 为了验证所提算法的性能,选取3幅常用的高光谱图像进行实验,并与SOMP[27]、Gabor[28]、IFRF[29]、CK-SVM[30]、CCJSR[15]等算法进行比较。每组实验数据集都是将原始高光谱图像进行归一化后得到,为了消除相关干扰,每组实验都进行10次后取平均值。 使用3个真实高光谱遥感数据集进行实验评价,分别是Indian Pines数据集、Salinas数据集和帕维亚大学(Pavia University)数据集。 Indian Pines数据集是在美国西北部印第安州的印度松试验场采集的部分图像数据。Indian Pines数据集是一个220波段的AVIRIS高光谱图像,图像大小为145×145像素,光谱分辨率为10 nm,空间分辨率为20 nm。但是由于第104~108、第150~163和第220个波段不能被水反射,因此一般选用剔除这20个波段后剩下的200个波段作为研究对象。该图像是在6月份采集的,一些农作物,如玉米和大豆,仍处于早期成长阶段,覆盖率不足5%。利用现场的参考分类,将场景划分为16个不同的类别,并且它们之间不完全相互排斥。图4展示了Indian Pines数据集的假彩色图像和地面真实图像。 图4 Indian Pines数据集 Salinas数据集是在美国加利福尼亚州的Salinas山谷获取的图像,是从3.7 m空间分辨率的AVIRIS传感器上获得的。该图像大小为512×217像素,去除原始图像中的20个水汽波段,最终留下剩余的204个波段。整个图像包含了16类地物,具体分类如图5所示。 图5 Salines数据集 Pavia University数据集是从意大利的帕维亚大学获得的图像,图像大小为610×340像素,共有115个波段,空间分辨率为1.3 m。其中12个波段由于受到噪声影响被剔除,使用剩下的103个光谱段所成的图像。Pavia University的假彩色图像和相应的地面真实图像如图6所示,场景被划分成了9类。 图6 Pavia University数据集 为了比较不同分类算法的性能,选取分类精度(classification accuracy,CA)、总体精度(overall accuracy,OA)及Kappa系数3个常用HSI分类指标作为评价标准[31]。其中,CA为图像中每个类别的分类精度,OA为总体正确分类的百分比。Kappa系数为一致性检验指标,CA和OA为检查有多少像素被正确分类的指标[32]。 在3幅常用的HSI图像上进行实验测试,与5种已有的分类算法相比较,验证本算法的有效性。根据Indian Pines、Salines和Pavia University图像的类别数和不同类别对应地面真实图像的形状规则度,对3幅图像分别随机抽取每类样本的5%、2%和8%作为标签样本集,其中标签集在每次运算中都进行重新采样,并且都是随机选择的。考虑到样本少的数据集按比例抽取后可能会很小,实验中设置每个样本的最小阈值为6,以此平衡样本间的差异性。对于超像素的数量,根据图像的大小及经验,分别设置3个HSI的LSC超像素为800、2 000和5 000。 表1~3给出了不同分类算法的10次实验分类结果对应的CA、OA和Kappa系数的平均值。其中,表中的数据为CA值,粗体代表最佳值。图7~9显示了在10次实验中最接近平均OA值的一次实验对应的分类图。 图7 Indian Pines数据集分类图 由表1~3的实验结果可以看出,本算法性能相对优于其他算法,虽然对于Pavia University数据集的分类精度比CK-SVM算法差,但仅相差0.42%,说明本算法鲁棒性相对较好。分析Indian Pines和Salines数据集的实验结果可以发现,无论这两个高光谱图像每个类的样本多少,相比其他方法,本算法的分类精度CA都保持着较高水平。对于Pavia University数据集,虽然其分类类别较少,且每个类的训练样本数量也最多,但其分类精度却不是很稳定,说明对于纹理相对较清晰的高光谱图像,超像素分割的引入,可以大大提高分类精度。对于每类区域分得比较细小、纹理相对比较复杂的高光谱图像,由于超像素分割的边缘契合度不是很高,导致分类精度降低。但相对于其他几种方法,本算法仍有较大优势,特别是相对于CCJSR算法而言,本算法无论是总体精度,还是分类精度都高出很多,也进一步说明超像素分割和谱聚类的引入提高了联合稀疏表示算法的分类效果。 表1 Indian Pines实验数据 表2 Salines实验数据 表3 Pavia University实验数据 针对高光谱图像空间分布一致性并非普遍存在,且存在同类异谱和异类同谱现象,导致高光谱图像分类精度大大降低的问题,提出基于线性谱聚类(LSC)超像素分割和联合稀疏表示算法。该算法利用LSC超像素分割从全局上考虑高光谱图像的数据特征,利用高光谱图像的光谱信息和空间信息,并且考虑了噪声及区域边界对分类效果的影响,消除了同类异谱和异类同谱现象对分类精度的影响,减少了类间干扰。实验结果表明,与其他5种算法相比,本算法不仅提高了总体分类精度,也大大提高了每个类的分类精度。特别地,LSC超像素分割以其良好的边界依附性和形状紧凑性,使本算法具有良好的鲁棒性。 图8 Salines数据集分类图 图9 Pavia University数据集分类图2.2 基于谱聚类和相关系数的联合稀疏表示算法
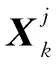
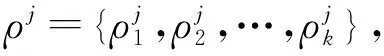
3 数值实验与结果分析
3.1 实验数据集

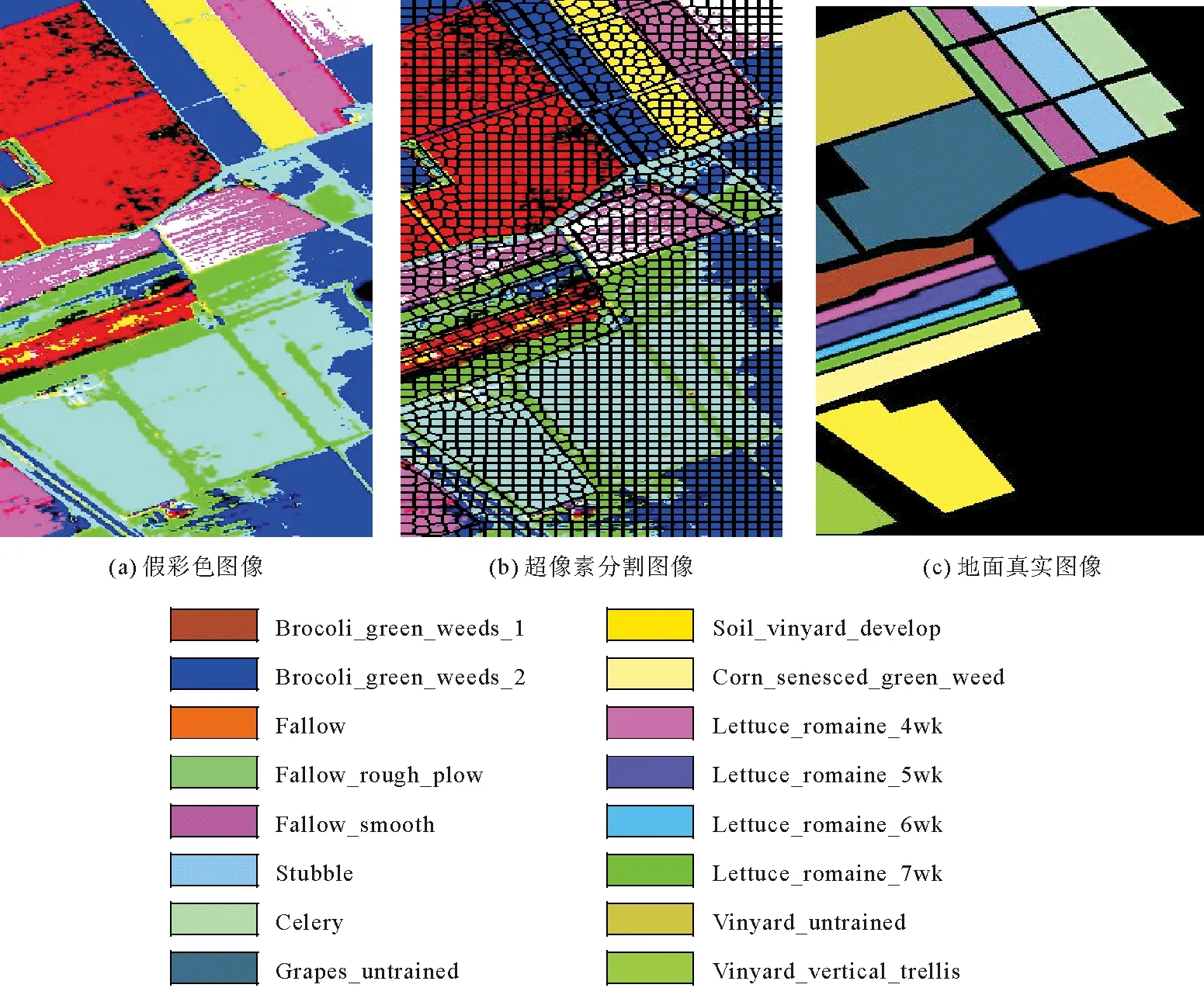

3.2 参数设置
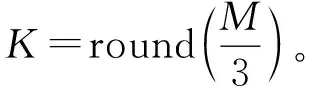
3.3 评价指标
3.4 实验结果分析
4 结论


