基于微平面模型和正则化的脆性岩石损伤破裂模拟方法

2022-08-12周广磊勒治华

东北大学学报（自然科学版） 2022年8期

袁阳，徐涛，周广磊，勒治华

(1. 东北大学资源与土木工程学院，辽宁沈阳 110819； 2. 山东科技大学能源与矿业工程学院，山东青岛 266590)

在外力和环境的作用下，由于细观结构缺陷(如微裂纹、微孔洞等)引起的材料或结构的劣化过程称为损伤.根据所采用的损伤力学理论，岩石损伤本构模型可分为宏观损伤模型和细观损伤模型[1].针对岩石、混凝土等准脆性材料非弹性力学行为与微裂纹张开、闭合、摩擦滑移等细观力学损伤机制，Bazant等对塑性滑移理论[2]进行拓展，建立了微平面模型(microplane model)[3-4]，其基本思想是直接以应力和应变的矢量而不是张量建立本构关系.经过不断发展，微平面模型已经成功用于混凝土、土和岩石的本构模型中[5].微平面是指在宏观连续介质体内任何一点的无穷小区域内垂直于任意方向的平面.与传统方法采用宏观连续介质应力、应变张量及其不变性来表达材料的本构模型不同，微平面模型通过在给定的材料点上作用于所有可能取向的单个微平面上的应力和应变矢量来描述材料在宏观尺度上的行为.这种从微观到宏观的分析方法为描述岩石的力学本构行为提供了新思路[6].

数值模拟方法在岩石破坏机理研究中获得广泛应用，而采用连续介质损伤力学方法在模拟岩石类材料破坏时会导致局部化也已成为共识[7-8]，这意味着有限元模拟分析中使用应变软化模型时会严重依赖于离散化网格的尺寸[9].Mondal等[10]认为这种全局响应对空间离散化表现出很强的依赖性的原因是当应用网格细化连续介质时，渐进损伤破坏区域的解不能收敛.崔焕平等[11]将损伤判定的极限拉应变值替换成与网格尺寸相关的函数来解决网格尺寸效应.Bazant等[12]将非局部理论用于分析准脆性材料损伤问题，初步发展了非局部损伤力学方法，并对积分型非局部模型进行了综述[13].基于准脆性材料在压缩和剪切状态下拉伸开裂和非线性三轴响应的微平面模型，Bazant等[14]提出了一种能够反映材料损伤和结构尺寸效应的非局部微平面模型.文献[15-16]基于ABAQUS有限元软件二次开发平台将非局部理论[17]嵌入M7微平面模型[18]中，对混凝土应变局部化的有限元网格敏感性进行了分析.但目前提出的微平面模型及其损伤均是通过在每个微平面上添加指数函数来表征微平面应力到达阈值后产生的应力软化从而影响宏观应力[16].

本文提出了一种基于有效应力概念的微平面损伤模型，通过引入非均质细观模型的思想[19]，摒弃了微平面中采用的应力边界假设，大大减少所需的力学参数.基于有限元软件COMSOL及MATLAB二次开发平台，将微平面非线性本构关系所采用的PDE(partial differential equation)形式嵌入程序中，编写了定义微平面损伤的相关程序，并在数值模型中引入高阶梯度正则化方法，通过在方程中定义材料的内部特征长度来防止局部化问题，模型中节点处的应力或应变状态不仅受到该点历史应力应变状态影响，而且还受到邻近节点状态的影响，一定程度上解决了有限元计算中的网格依赖性问题.

1 数值模型与方法

1.1 微平面模型

微平面模型通过应力率和应变率之间的关系构建微平面上本构关系来描述宏观应力应变与时间之间的变化关系.其基本假设有静态约束和动态约束，动态约束指微平面上的应变等于宏观应变张量εij的投影分量，其宏观应变张量与微平面上的应变分量直接相关，而静态约束则是指微平面上的应力等于宏观应力张量σi,j的投影分量，其宏观应力张量与微平面上的应力分量直接相关[20].本文采用的动态约束适用于描述微平面应变沿各方向连续变化，而微平面应力沿各方向变化不连续的情况，微平面上法向、切向应变分量与宏观应变张量之间的关系可表示为

(1)

式中:ni为微平面空间法向向量；mi,li为切向向量分量，i，j=1,2,3；εN,εM,εL(N为法向，M, L为切向T分解的分量)分别为动态约束条件下微平面上的法向和切向应变，其在微平面上的关系如图1所示；Nij,Mij,Lij具有对称性，其定义如下：

(2)

图1为2×21个积分点微平面模型，其空间形状为一正二十面体，积分点(微平面)的位置为其顶点(12个)和棱中点(30个)[21].以应变率和应力率形式表示的微平面本构关系(式(3))能够很好地描述模型应力应变与时间的联系[22]，该关系在COMSOL中通过添加PDE物理场来实现.

(3)

其中，EN,ET分别为法向和切向弹性常数，其与单元的弹性模量关系为

(4)

式中，υ为单元节点的泊松比.

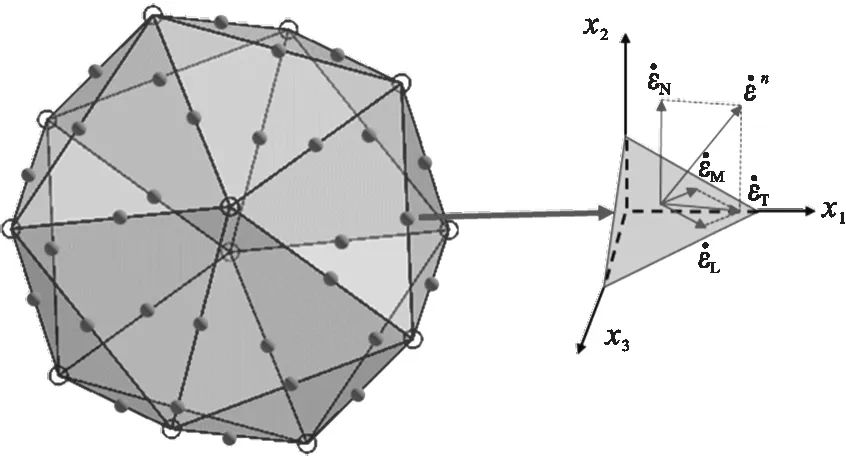
图1 微平面上应变率矢量的分量

宏观应力张量为微平面应力在各积分点上不同方向进行积分求值之和，为在程序中更好地进行计算，宏观应力张量与微平面应力矢量通过不同方向积分后的近似关系如式(5)所示，其积分点的空间位置及权重详细论述可见文献[6].

(5)

式中：n代表总的积分点数目;k表示某一微平面；ωk为微平面k的权重.

1.2 微平面损伤模型

基于应变等效假设[23]的损伤在细观损伤力学模型中已得到广泛的应用[24-26]，其基本思想是将无损材料中的名义应力以有损材料的有效应力代替建立的损伤本构关系.有损材料的弹性模量定义为

E=E0(1-D) .

(6)

式中:E0为材料的初始模量;D为损伤值(0≤D≤1).

本文提出的微平面损伤模型的应力状态基于屈服准则判定.首先，对于处于拉应力状态时的节点，即法向应力为正(σN> 0)的情况采用最大拉应力准则，认为某个微平面上的最大法向应力超过阈值时，该微平面系统对应的节点即发生损伤，可表示为

(7)

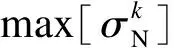
当单元处于压缩状态(σN≤0)时，采用Mohr-Coulomb(MC)屈服准则.在微平面系统中可以理解为当单元的某个微平面上的正应力和剪应力满足该条件时发生剪切破坏，可表示为

(8)

D=D(n) .

(9)

对于单个微平面而言，损伤仍然是一个标量.对于某一单元节点，发生拉伸损伤时，其发生损伤的微平面方向的值可以表示为

(10)

其中：εN为微平面法向应变；εt0为开始发生损伤的拉伸应变值；η为残余强度系数；εtu为该微平面对应的极限拉伸应变.发生剪切损伤时，损伤值可表示为

(11)

其中：εc0为微平面法向应变εN小于零时对应的最先发生剪切破坏的微平面所对应的压缩应变阈值；σc0为最先发生剪切破坏的微平面上的极限压缩应力值.为了区别不同损伤值，对满足最大拉应力破坏准则的拉伸损伤规定为负值，对满足MC屈服准则的剪切损伤规定为正值.

1.3 正则化方法引入

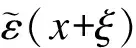
(12)

式中,∇n为n阶梯度.又因为

(13)

式中:∇2为拉普拉斯算子;系数α,β为高阶项系数.由式(13)可得

(14)

将式(14)代入式(12)并略去高阶项，可得

(15)

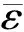
1.4 岩石的非均质表征

岩石由各种晶粒、胶结物和孔隙组成，为表征其非均质特性，假设其内部细观参数服从Weibull分布：

(16)

式中:u为岩石细观参数(弹性模量、强度、内聚力等);u0是一个与单元参数平均值有关的参数;m为非均质系数.从图2可知，随着非均质系数的增大，细观参数的分布范围变得愈加狭窄，表示岩石内部参数愈均匀.将Weibull分布函数引入数值模型中，其物理意义在于表征岩石的非均质性，在数值模型中可以防止大量单元在同一加载步出现损伤，其次，此方法可以体现出材料的“宏观塑性”[25].

图2 非均质系数m对应的概率密度分布(弹性模量)

2 模型在COMSOL中的实现及验证

微平面模型需要针对每一个微平面构建本构关系，本文模型基于COMSOL Multiphysics 5.2 和MATLAB平台进行二次开发.

2.1 模型在COMSOL平台实现过程

通过在COMSOL中建立微平面损伤模型，在MATLAB平台中加入循环函数以实现岩石参数(弹性模量、强度、内聚力和损伤)的每一步求解后的更新迭代.具体流程(见图3)为，先对每一个方向上的微平面本构关系在COMSOL界面中通过添加PDE物理场以建立微平面上的应力-应变随时间变化的关系，如需建立2×21个积分点的微平面模型，则需要建立21个物理场，每个物理场中包含3个偏微分方程对应式(3)，对于本文中的数值模型，表征微平面模型共建立63个偏微分方程.计算流程为首先对每个单元节点上的局部宏观应变增量根据式(1)进行分解，即微平面k上的微平面法向应变矢量为非局部应变张量与法向投影张量的乘积(动态约束).对于每一个应变分量，可以建立Helmholtz方程通过式(15)进行局部应变和非局部应变之间的替换.值得注意的是，本文中采用正则化模型对三点弯曲实验进行模拟，该实验预制裂缝处主要为拉伸破坏.因此为减少计算量，本文只对微平面法向应变进行非局部变量的替换，而切向应变则不替换.得到微平面非局部应变矢量分量后，根据微平面本构关系式(3)进行微平面应力的计算，继而根据微平面上的损伤状态进行判断是否需要对单元的弹性模量进行折减，最后通过高斯公式进行数值积分得到该加载步下的宏观应力张量.

2.2 模型验证

根据上述步骤，编写基于微平面损伤模型的MATLAB程序，为节省计算资源，选取单位球面积分点数目为2×21.实验建立了单轴压缩模型，试件尺寸为直径25 mm，高62.5 mm.数值模型和花岗岩参数如表1所示.值得注意的是，数值模拟的弹性模量和强度是单元的平均值[27]，而实验中的弹性模量和强度是实验结果.

图4绘制了数值模型和实验的应力-应变曲线，实验开始加载阶段为孔隙压密阶段，后线性部分为弹性阶段，接近峰值时出现非线性阶段，试件达到峰值强度162.3 MPa后破坏，由于实验过程的应变通过应变片来采集，故不能显示峰后阶段.

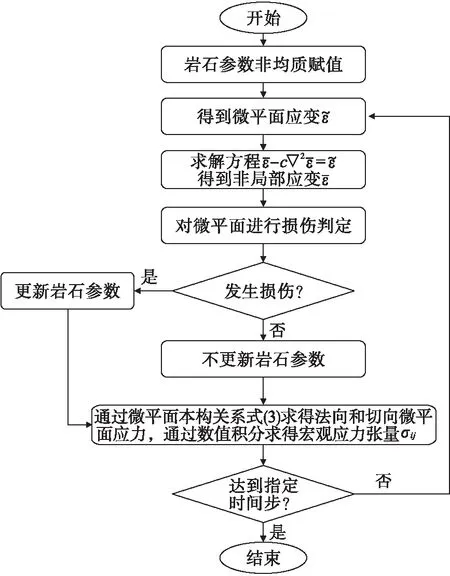
图3 基于微平面损伤模型的正则化方法计算流程图

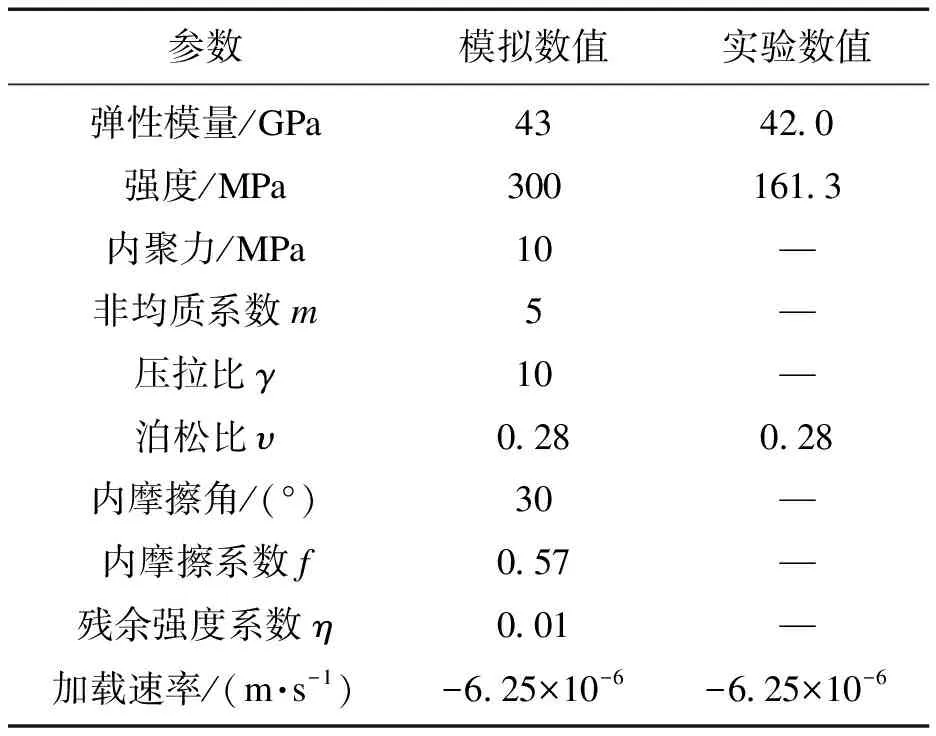
表1 单轴压缩实验和模拟的材料参数

本文提出的微平面损伤模型并未假设孔隙压密阶段，因此不能表征这一阶段.图4中的点划线为数值模拟线性阶段平移曲线，可知对于弹性阶段和接近峰值的非线性阶段以及峰值强度，数值结果与实验结果较为吻合.

限于篇幅，图5只给出了单轴压缩数值模拟结果的部分损伤演化过程图，图例中不同数值代表损伤值的种类和大小.根据1.2节定义正值为压缩状态下的剪切损伤，负值为拉伸损伤，绝对值越大代表该种损伤越大.在开始加载阶段，模型损伤为零.随着加载步增大，试件随机出现了剪切和拉伸损伤，在短时间内，这些损伤逐渐汇聚贯通，最后与单轴压缩实验中的试件相同形成剪切带.而数值模拟在第66～68步恰好为峰值强度后出现应力跌落.结果表明，模型能够较好地反映岩石在应力加载条件下的损伤演化过程.

图4 单轴压缩数值模拟和实验结果应力-应变曲线

图5 单轴压缩数值模拟和实验破坏结果对比

3 正则化模型分析

采用微平面损伤模型(本文称之为普通模型)得到的宏观变形、应力及损伤发展依赖于有限元网格尺寸和数量.本文采用三点弯曲试件进行正则化方法分析，试件尺寸如图6所示，底部2个支座固定，试件跨度为70 mm，试件长度为90 mm，试件高度为30 mm，宽度为10 mm，预制裂缝a为宽1 mm，高4 mm.在数值模拟中，倘若常采用圆柱作为上下支点，其与试件为线接触，在进行损伤迭代计算时，易于在支点处产生应力集中发生破坏，与实际情况不符.为获得良好的计算结果，本文将圆柱体与试件接触改为宽2 mm，长10 mm的矩形接触面，加载速率为1×10-6m/s.

3.1 非均质系数对损伤的影响

首先对不同非均质系数(1，5和10)的微平面损伤普通模型在不同时间加载步下的破坏模式

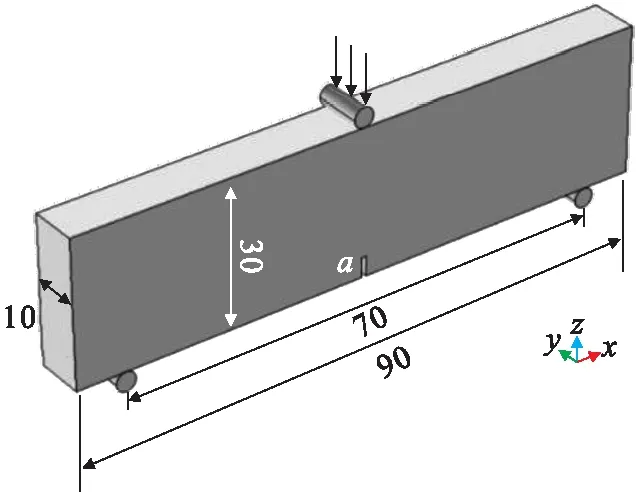
图6 三点弯曲实验试件尺寸(单位：mm)

进行对比分析.除加载速率外数值模型参数见表1.为提高模型计算速度并防止网格收敛性问题，模型网格划分采用COMSOL默认的四面体网格(Mesh1)，最大单元尺寸为3.15×10-3m，最小单元尺寸为1.35×10-4m，最大单元增长率为1.35，单元总数为70 109个.图7给出了不同非均质系数m的试件损伤演化.由图7可见，非均质系数对试件的损伤破坏影响明显，非均质系数低(m=1)时，岩样中损伤在预置裂缝周围弥散分布；非均质系数高(5，10)时，岩样中损伤集中于预置裂缝尖端，形成明显的局部化损伤区域.非均质系数为1时，损伤区域虽然在预制裂缝处较多，但是在试件其他区域也有大量损伤区域存在，与实际情况不符.对于岩石材料而言，非均质系数为5左右时结果较为合理[25-27].

3.2 特征长度对损伤影响

根据有限元模型网格尺寸(1.35×10-4～3.15×10-3m)，采用特征长度分别为0.3，0.4，0.5，1，2 mm进行数值模拟，数值模型非均质系数均为5，网格划分方式(Mesh1)是由COMSOL根据物理场自动生成的四面体形式.图8为具有不同特征长度的数值模型的损伤云图(时步为50)，图例中的数值其意义与2.2节中相同.从图8可知，采用相同网格划分方式，正则化模型与普通模型的破坏模式大致相同.因此正则化模型可以看作是对普通微平面损伤模型中某些变量(如应变)的修正，并不会导致结果产生巨大差异.并且，在相同网格划分下，特征长度越小，越接近最小网格尺寸，损伤效果越好；特征长度为0.4 mm和 0.3 mm 时损伤位置和损伤发展方向准确，但最终损伤效果与特征长度为0.5 mm的结果相近，因此模型单元尺寸与特征长度相近时，可认为对损伤结果影响较小.特征长度(l=2 mm)过大时，由于特征长度大于大部分网格尺寸，导致损伤面积过大而不符合实际情况.由此可见，在相同网格划分条件下，存在一个最优特征长度值，可以得到最好的裂纹扩展效果.在可预见的范围内，对相同尺寸的数值模型而言，随着网格密度增大，最小单元尺寸减小，最优特征长度值也会随之减小.

图7 不同非均质系数的试件损伤演化

图8 不同特征长度的损伤演化

3.3 网格敏感性分析

采用第二种较稀疏的网格(Mesh2)进行数值模拟，均质度为5.图9为普通和正则化模型三点弯曲数值模型在两种网格情况下第50步时局部损伤云图，图中Mesh1网格的最大单元为3.15×10-3m，最小单元为1.35×10-4m，总单元数量为70 109个，Mesh2网格的最大单元尺寸为7.2×10-3m，最小单元尺寸为9×10-4m，总单元数量为10 772个.图中正则化模型采用的特征长度为1 mm.可以得知，在改变网格密度后，在相同加载步数下，普通微平面模型的破坏模式发生了较大的改变，损伤区域长度变短，并且与裂缝平行的相邻单元也发生了损伤.而对于正则化模型而言，改变网格密度后，其破坏区域大小和方向基本保持不变，说明引入正则化方法后，模型损伤结果对网格依赖性较小.

图9 普通模型和正则化模型两种网格密度损伤演化

对两种网格划分Mesh1和Mesh2的载荷-位移曲线进行普通模型和正则化模型的对比分析.载荷为施加在试件上部区域的z方向反力，位移为施加载荷的区域z方向位移.图10为普通和正则化模型在两种不同网格密度下对三点弯曲试件进行数值模拟，其中正则化模型的特征长度为1 mm，非均质系数为5.由图10可知，随着网格密度减小(网格尺寸增大)，普通模型模拟的强度发生了明显变化，此为有限元计算过程中出现的相同模型由于网格尺寸大小、密度不同产生的尺寸效应.总体而言，模型在引入正则化方法后，试件的整体强度和应变峰值增大，但不同网格密度大小对正则化模型的载荷-位移曲线影响较小，二者趋势在第40计算步之前基本一致，这是由于正则化微平面损伤模型可以考虑单元与有限范围内单元之间的影响，这样减少了由于损伤局部化引起的单元网格敏感性，保证了数值模拟结果的客观性.而在峰后阶段(第40计算步后)载荷-位移曲线相差较大，其原因可能是本文提出的损伤模型不涉及峰后阶段的岩石力学行为，该部分工作将于今后开展.