基于IMOFA的航空发动机管路多目标优化布局
2022-08-12巩亚东
张 禹, 鹿 浩, 吕 董, 巩亚东
(1. 东北大学 机械工程与自动化学院, 辽宁 沈阳 110819; 2. 东北大学 航空动力装备振动及控制教育部重点实验室,辽宁 沈阳 110819)
管路系统是航空发动机的重要组成部分,其布局设计质量严重影响着航空发动机的性能、使用寿命和成本.在实际生产中,航空发动机的管路布局设计主要由经验丰富的工程师手工完成,这种传统的设计方法非常耗时,也难以获得最佳的管路布局,极大地阻碍了航空工业的发展.因此,航空发动机自动管路布局设计已成为亟待解决的热点问题.
国内外学者和研究机构对管路自动布局作了很多有意义的研究.Christodoulou等[1]采用蚁群算法解决了城市配水管路的布局.董宗然等[2]提出一种最短路径快速算法,并采用该算法实现了船舶管路的自动敷设.Liu[3]提出了一种基于曼哈顿可视图的管路敷设算法,用以寻找航空发动机管路最短路径.上述文献都侧重考虑管路长度最短为优化目标,优化目标单一,导致布局效果不理想.考虑管路长度最短和弯头数最少作为管路布局优化目标,Jiang等[4]提出了一种协同进化多蚁群优化算法的船舶管路布局设计方法;Qu等[5]应用3D连接图和并行蚁群优化算法对航空发动机管路进行了布局优化;Min等[6]提出了一种基于跳点搜索的管道自动布线算法.此外,赵柏萱等[7]提出一种基于快速扩展随机树算法和模拟退火算法的航空发动机管路自动布局与优化方法,该方法解决了以管路长度最短和流阻最小为优化目标的管路布局问题.考虑管路长度最短、弯头数最少和能量值最小作为管路布局优化目标,Wu等[8]采用改进的蚁群优化算法对半潜式采油平台的管路布局问题进行了研究;Dong等[9]将A*算法和遗传算法相结合对船舶管路布局问题进行了研究.上述文献虽然考虑了多个优化目标,但都是通过加权的方式将管路的多目标优化布局问题转化为单目标进行优化,并没有真正解决多目标优化问题,导致布局效果欠佳.
综上所述,虽然这些研究工作取得了一定成果,但目前研究只针对单个目标或将多个目标以线性加权的方式转化为单个目标进行管路自动优化布局,这导致管路布局质量不佳.多目标萤火虫算法[10]是一种启发式群智能优化算法,具有参数设置少、鲁棒性和寻优能力强等优点,适用于解决多目标优化问题.因此,针对上述问题,本文对基于改进多目标萤火虫算法的航空发动机管路智能布局方法进行了研究.
1 管路布局数学模型
一个典型的航空发动机通常包含数百根管路,这些管路在布局过程中不仅要考虑空间限制,而且还要考虑多样的设计要求和众多的工程规则,这使得航空发动机管路布局成为多目标复杂优化问题,在理论上属于NP-hard问题.考虑到管路布局的经济性和可靠性设计要求以及工程规则,本文以管路路径最短、管路弯头最少和管路能量值最小作为优化目标,并考虑弯曲半径和夹角等约束条件,建立了航空发动机管路多目标优化布局数学模型.
1.1 目标函数
为了减少管路布局的成本和提高管路布局的可靠性,所建立的管路布局目标函数如下:
1) 管路长度目标函数
(1)
其中:L为管路长度;li为该管路第i段的长度,1≤i≤n;n为管路的管段数.
2) 管路弯头数目标函数
(2)
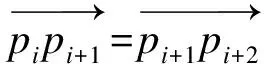
3) 管路能量目标函数
(3)
其中:E为管路能量;

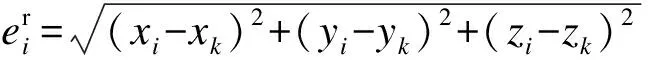
1.2 约束条件
根据管路布局的工程规则[11],本文所考虑的约束条件如下:
1) 弯曲半径约束
rbend≥R.
(4)
其中,rbend表示弯头的弯曲半径.当D≥20 mm时,R≥2D,当D<20 mm时,R≥D,其中D为管路外径.
2) 夹角约束
θbend=π/2 .
(5)
其中,θbend是相邻两段管路之间的夹角.
3) 直段长度约束
dmin_length≥2.5rbend.
(6)
其中,dmin_length表示敷设管路d的直线段长度.
4) 距离约束
ddistance≥λ1L1+λ2L2+λ3L3.
(7)
其中:L1为管路之间、管路与相邻一般附件之间的最小间隙;L2为管路与热源等特殊附件之间的最小间隙;L3为管路和刚性固定处的最小间隙,L1,L2和L3值由技术人员指定;当管路与管路或管路与一般附件相邻时,λ1=1,λ2=0,λ3=0,当管路与特殊附件(如热源)相邻时,λ1=0,λ2=1,λ3=0,当管路与刚性固定处相邻时,λ1=0,λ2=0,λ3=1.
5) 跨度约束
θangle<π .
(8)
其中,θangle表示敷设管路的圆周跨度.
1.3 数学模型
基于以上讨论,将管路节点坐标作为变量,把管路布局中的工程要求作为约束条件,以最短管路路径、最少管路弯头和最小管路能量值为优化目标建立的管路布局数学模型为
(9)
2 应用于航空发动机管路布局的改进多目标萤火虫算法
萤火虫算法[12]是一种模拟自然界萤火虫种群之间求偶、觅食行为的启发式群智能优化算法,由于该算法具有操作简单和鲁棒性强等优点,在单目标优化问题方面已经取得很好的效果.由于它的种群搜索特性和良好的性能,近些年已被用于解决多目标优化问题,因而多目标萤火虫算法被提出和关注[13].目前,多目标萤火虫算法的研究尚处于起步阶段,传统的多目标萤火虫算法存在易陷入局部最优和搜索效率低下等问题.因此,本文在传统多目标萤火虫算法的基础上,基于非支配关系、拥挤度和约束违反值建立了个体多目标评价函数.进一步,结合自适应扰动策略和精英策略,提出应用于航空发动机管路多目标优化布局的改进多目标萤火虫算法,其流程图如图1所示.
1) 萤火虫编码.萤火虫编码采用变长度编码的方式,编码方式如下:
path={(xs,ys,zs),…,(xi,yi,zi),…,(xt,yt,zt)} .
(10)
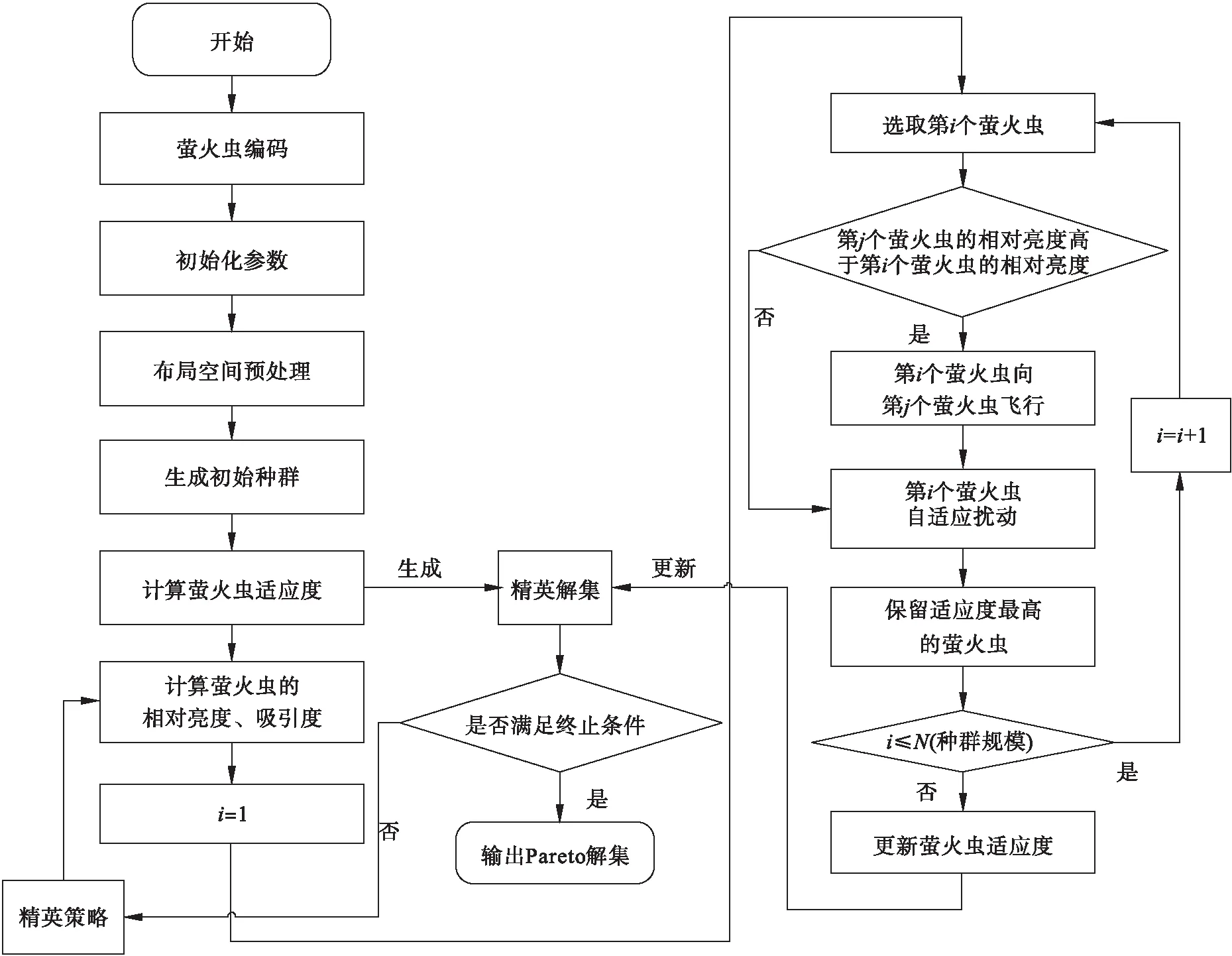
图1 基于改进多目标萤火虫算法的航空发动机管路布局流程图
其中:一条管路路径path表示一个萤火虫;(xs,ys,zs)表示起始节点的坐标,(xi,yi,zi)表示第i个节点的坐标,(xt,yt,zt)表示目标节点的坐标.
2) 初始化参数.设置种群规模N,最大吸引度β0,光强吸收系数γ,最大迭代次数Tmax,精英解集大小M.
3) 布局空间预处理.通过将布局空间沿机匣母线展开3次并进行拼接,从而实现回转体布局空间向立方体布局空间的转化,如图2所示.
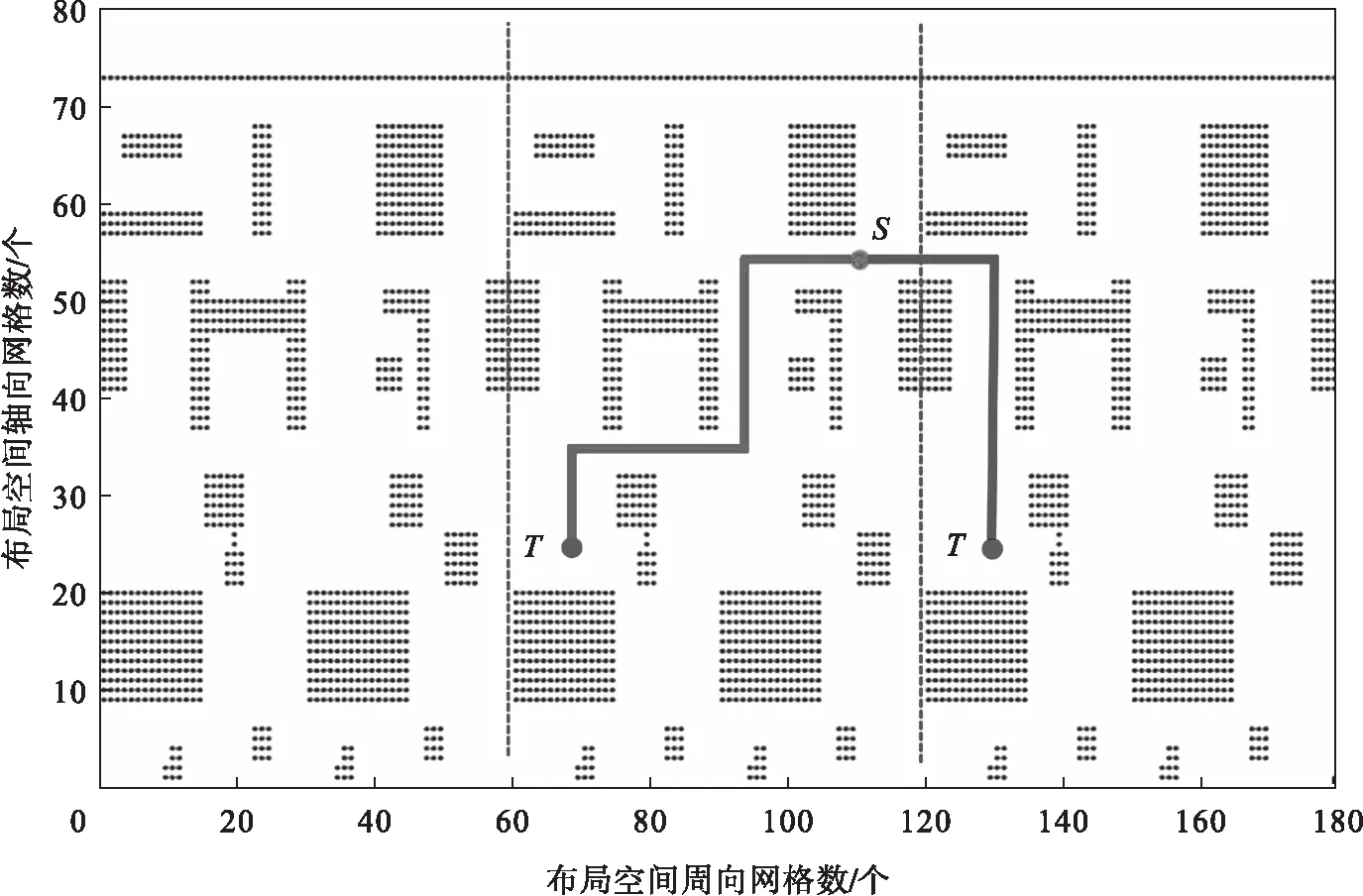
图2 布局空间预处理示意图
4) 生成初始种群.为了得到多条不同的可行初始路径,通过增大路径节点的启发式代价值来改进传统A*算法[14],从而生成多条不同路径,进而得到初始种群.
5) 计算萤火虫适应度.为了提升管路个体寻优质量和效率,本文基于非支配关系、拥挤度和约束违反值建立个体多目标适应度函数,其主要思路为:通过非支配关系对种群个体进行非支配分层,即如果个体A(L,B,E)<个体B(L,B,E),则表示个体A支配个体B,通过该种方式对种群中任意2个个体进行比较,进而实现个体的非支配分层.在此基础上,基于拥挤度和约束违反值对同一层的非支配个体进行排序,即对于满足约束的个体,采用式(11)计算其拥挤度实现同一层个体的优劣评价;对于违反约束的个体,采用式(12)计算约束违反值,实现同一层个体优劣评价.进而,通过种群的最大支配层数、个体所在的非支配层数和个体所在非支配层的优劣程度来建立萤火虫个体的多目标适应度函数F(x).
(11)

(12)
其中:CV(x)为萤火虫的约束违反值;
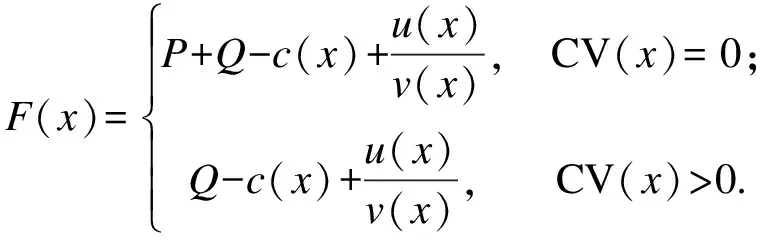
(13)
其中:P和Q分别为满足约束(CV(x)=0)和违反约束(CV(x)>0)萤火虫个体的最大非支配层数;c(x)为萤火虫个体所在的非支配层数;v(x)为萤火虫个体所在的非支配层中萤火虫的数量;u(x)为萤火虫个体所在非支配层中的序列号(当CV(x)=0,根据拥挤度大小排序得到序列号;当CV(x)>0,根据约束违反值大小排序得到序列号).
6) 生成精英解集. 根据式(13)计算初始种群中萤火虫的适应度,保留当代最优的非支配解,进而生成精英解集.
7) 计算相对亮度、吸引度.根据式(14),计算萤火虫的相对亮度:
(14)
其中:I0为萤火虫的最大荧光亮度,即自身(r=0处)荧光亮度,与适应度函数值有关;γ为光强吸收系数;rij为第i个萤火虫和第j个萤火虫之间的距离,其计算公式为
(15)
其中:设第i个萤火虫的编码长度大于第j个萤火虫的编码长度,则n为第i个萤火虫的编码长度;(xik,yik,zik)为第i个萤火虫第k个节点的坐标;(xjk,yjk,zjk)为第j个萤火虫第k个节点的坐标.
根据式(16),计算萤火虫的吸引度:
(16)
其中,β0为最大吸引度,即光源处(r=0处)的吸引度,一般取1.
8) 萤火虫飞行.选取第i个萤火虫,当存在第j个萤火虫的相对亮度高于第i个萤火虫的相对亮度时,选取第j个萤火虫中适应度最高的一段路径作为继承路径(继承路径在第j个萤火虫中的占比为吸引度β),用继承路径替换第i个萤火虫中相对应的路径段,并用改进A*算法进行衔接,生成新的路径,得到萤火虫i′;若不存在第j个萤火虫的相对亮度高于第i个萤火虫的相对亮度,则对第i个萤火虫执行步骤9).
9) 萤火虫自适应扰动.为了提高算法的全局搜索能力,本文采用自适应扰动策略进行萤火虫个体更新,其主要思想为:萤火虫适应度越低,其扰动越大,从而提升萤火虫寻优的质量和效率.具体步骤为:选取萤火虫i′中适应度最低的一段路径(该段路径在萤火虫i′中占比为α|rand-1/2|,其中自适应扰动因子α=(I0max-I0)/(I0max-I0min),I0max为当前种群适应度最高的萤火虫的最大荧光亮度,I0min为当前种群适应度最低的萤火虫的最大荧光亮度),应用改进A*算法重新生成该条路径,得到萤火虫i″,计算萤火虫i′和萤火虫i″的适应度,保留适应度最高的萤火虫.
10) 判断当代种群是否更新完毕.如果当代所有萤火虫完成位置更新,则进行下一步,否则返回步骤8).
11) 更新萤火虫适应度.根据式(13),计算位置更新后的萤火虫的适应度.
12) 更新精英解集.将位置更新后的非支配解添加至精英解集,并根据式(13)得到精英解集的新的非支配解.
13) 终止条件判断.终止条件为迭代次数.如果满足,从精英解集中输出Pareto解集,否则执行精英策略,即将当前种群中适应度最低的萤火虫替换为精英解集中适应度最高的萤火虫,并返回步骤7).
3 算法性能分析与实例研究
3.1 算法性能分析
在MATLAB中设置种群规模N=50,最大迭代次数Tmax=1 000,精英解集大小M=100,应用测试函数CF1(见式(17))对经典多目标粒子群优化(multi-objective particle swarm optimization,MOPSO)算法[15]、传统多目标萤火虫算法(multi-objective firefly algorithm,MOFA)和本文提出的改进多目标萤火虫算法进行了性能对比分析,如图3所示.
(17)
IGD指标是反映算法收敛性、均匀性和分布性的综合指标,其值越小越接近于0,算法的性能越好.由图3a可以看出,改进多目标萤火虫算法的IGD始终小于经典多目标粒子群优化算法和传统多目标萤火虫算法的IGD,到第240次迭代时几乎接近于0,故改进多目标萤火虫算法的收敛性、均匀性和分布性更好.由图3b可以看出,改进多目标萤火虫算法求得的Pareto最优解集很好地拟合了真实Pareto前沿,进一步验证了所提算法的性能优越性.
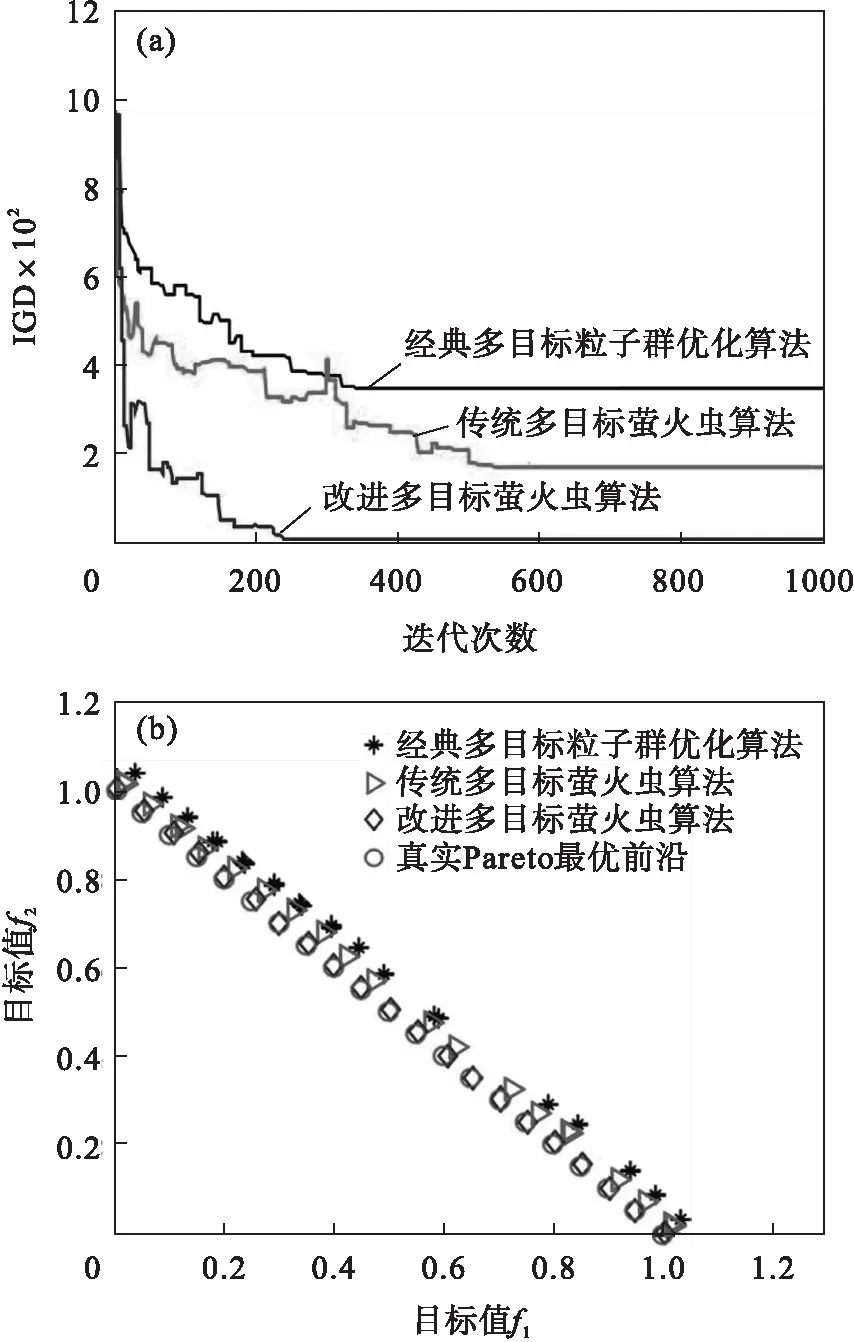
图3 三种算法性能对比
3.2 实例研究
图4给出了某航空发动机三维模型,该模型包含18个障碍物,管路布局空间范围为θ∈[0,2π],y∈[0,2 000],r∈[250,850],敷设管路的外径为15 mm.设置种群规模N=10,最大吸引度β0=1,光强吸收系数γ=1,最大迭代次数Tmax=30,精英解集大小M=20,加速度系数c1=c2=1.496 2;惯性权重系数ω=0.729 8.
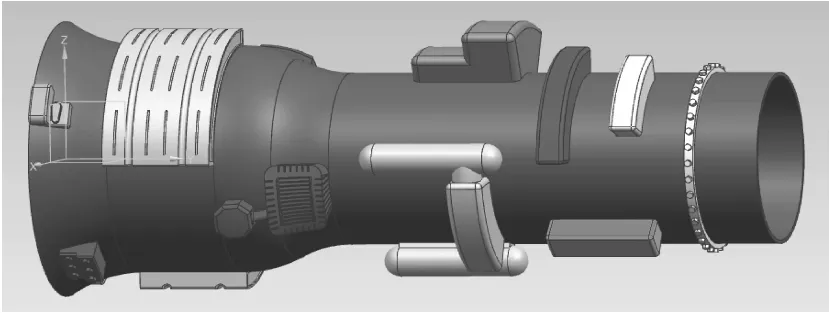
图4 某航空发动机布局空间三维模型
通过MATLAB分别基于经典多目标粒子群优化算法、传统多目标萤火虫算法和改进多目标萤火虫算法得到上述航空发动机管路布局Pareto解集,如表1~表3所示.由表1可知,通过经典多目标粒子群优化算法可以得到3个非支配解,非支配解1的管路弯头数最少,非支配解2的管路长度最短,非支配解3能量值最小, 各个解各有其优势,相互为非支配关系.由表2可知,通过传统多目标萤火虫算法得到4个非支配解,其中非支配解1的管路弯头数最少,非支配解2的管路长度最短,非支配解4能量值最小,非支配解3为折中解,各个解各有其优势,相互为非支配关系.由表3可以看出,通过改进的多目标萤火虫算法可以得到5个非支配解,非支配解1的管路弯头数最少,非支配解2的管路长度最短,非支配解5能量值最小,非支配解3和非支配解4为2个折中解,各个解各有其优势,相互为非支配关系.对比表1、表2和表3可以看出,表3中非支配解个数多于表1和表2中非支配解个数,且表1和表2中的非支配解普遍被表3中的非支配解所支配.在此基础上,应用UG(unigraphics)生成的航空发动机管路布局三维模型,如图5所示.

表1 基于经典多目标粒子群优化算法的管路布局 Pareto解集Table 1 Pareto solution set for pipe routing obtained by classical MOPSO algorithm
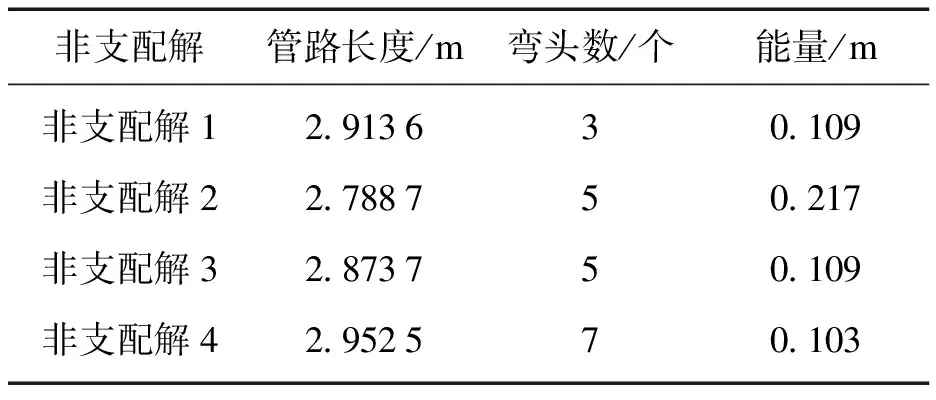
表2 基于传统多目标萤火虫算法的管路布局Pareto解集Table 2 Pareto solution set for pipe routing obtained by traditional MOFA

表3 基于改进多目标萤火虫算法的管路布局Pareto解集Table 3 Pareto solution set for pipe routing obtained by IMOFA
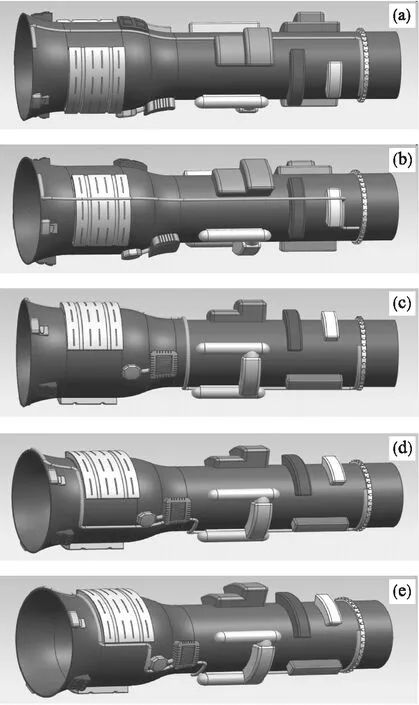
图5 基于改进多目标萤火虫算法的管路布局三维模型
4 结 论
1) 以最短管路长度、最少弯头数和最小能量值为优化目标,并综合考虑弯曲半径、夹角、长度、距离和跨度约束条件,建立了较全面的航空发动机管路多目标优化布局数学模型,为实现管路布局的多目标优化奠定了良好的基础.
2) 结合非支配关系、拥挤度和约束违反值,提出了一种新颖的管路多目标评价方案,为提升管路个体寻优质量和效率提供了条件.
3) 融合自适应扰动策略和精英策略,提出一种改进多目标萤火虫算法,获得较好的符合工程条件的多种航空发动机管路布局方案,提高了管路布局质量和效率,为实现管路智能化布局设计提供有力的技术支撑.
