基于BP神经网络的同步发电机短路故障模式识别

郑金艳 ，李 琰，范 玮

(1.安徽粮食工程职业学院,安徽 合肥 230011；2.合肥经济学院 工学院，安徽 合肥 230011)

同步电机是电力系统中最重要的元件，用于产生电能。同步电机本身的结构也较复杂，由多个有磁耦合关系的绕组构成，定子绕组同转子绕组之间有相对运动，同步电机突然短路的暂态过程要比稳态对称运行时复杂得多[1-4]。在稳态对称运行时，电枢磁动势不随时间变化，以同步速度旋转，并与转子没有相对运动，转子绕组中不会产生感应电流。当突然短路时，定子电流发生剧烈变化，定子和转子绕组电流相互影响，对同步发电机的损伤极大，严重影响发电机使用寿命，同时对末端负载也有高强电流冲击，损伤用电器，所以对同步发电机突然短路故障进行仿真分析、故障诊断及排除研究是非常必要的[5-8]。然而，故障诊断与定位为电力系统保护带来了一定的技术挑战，因此国内外学者针对高功率电机故障模式、仿真技术、智能识别算法的研究越来越多[9-11]。BP神经网络是一种误差逆向传播的多层前馈网络，能学习和存贮大量的输入-输出模式映射关系，在生产、生活及工程中应用广泛[12-13]。孙子明等[14]以双馈风力发电机为研究对象，基于BP神经网络，建立了遗传优化BP神经网络模型，对双馈风力发电机定子匝间短路特征进行了分析，并以定子电流为故障信号，进而实现不同程度的定子匝间短路故障的诊断与识别，为BP神经网络故障模式识别研究提供了参考。刘英等[15]认为励磁绕组匝间短路故障对电机组及负载的影响很大，不仅会增大电机的励磁电流，同时会减小输出无功功率，还会导致机组的振动加剧，严重影响系统安全运行，文中提出了一种以定子分支电流实现转子匝间短路故障定位的方法，以白莲河抽水蓄能电站2号机组为研究对象，对机组模型进行了仿真分析，结果表明了方法的有效性，可以为发电机组短路故障仿真、诊断提供参考。Zhang[16]在电机和相关部件(如绕组和滚珠轴承)中进行了故障诊断研究，提出了电机匝间短路故障短路比和短路电阻概念，推导了具有匝间短路故障的电机原理模型，该模型可通过估计短路比和短路电阻来估计故障的严重程度，并在MATLAB/Simulink中对电机匝间短路问题进行了仿真，结果验证了方法的可靠性，为发电机短路故障模型的建立提供了参考。

首先建立了同步发电机短路故障数学模型(以标幺值表示，p.u.)，给出定子d轴和q轴的电流分量、相电流、转子绕组电流计算公式，并在MATLABSimulink环境中搭建15 kV，50 Hz，200 MV·A同步发电机短路故障仿真模型，进行了8种模式的仿真，以得到同步发电机定子电流在各短路故障模式下的变化情况；分析了BP网络拓扑图，建立其反向传播算法模型。最后以短路故障定子电流变化的80%数据量作为BP网络的输入，训练得到同步发电机短路故障模式识别器；以剩余数据作为BP模式识别器的测试数据，进行多数据点故障识别，为同步发电机短路故障模式BP网络识别研究提供参考。

1 同步发电机短路故障模型

1.1 短路故障数学模型

利用叠加原理，同步发电机端突然短路相当于在电机端口突然加上了与发电机短路前的端电压大小相等，方向相反的三相电压。短路产生时，定子绕组电流包括基频分量、倍频分量和直流分量，转子绕组包括直流分量和同频率的交流分量。

定子d轴和q轴的电流分量分别为

(1)

式(1)中:xd,xq分别为定子绕组纵轴、横轴的同步电抗；x′d，x″d分别为纵轴暂态电抗、次暂态电抗；x″q为横轴次暂态电抗；E′q，E″q分别为横轴暂态电动势、次暂态电动势；E″d为纵轴次暂态电动势；Eq[0]，V[0]分别为短路前瞬间的控制电动势、机端电压；δ0为同步发电机初始功角；ω为电机转动角频率；T″d为d轴同步频交流分量二次指数衰减常数；T′d为d轴同步频交流分量一次指数衰减常数；Td为d轴同步频交流分量指数衰减常数；T″q为q轴同步频交流分量二次指数衰减常数；T′q为q轴同步频交流分量一次指数衰减常数；Tq为q轴同步频交流分量指数衰减常数。

以A相为例，可得A相电流为

式(2)中:α0为A相交流电初始相位；δ为同步发电机功角；Ta为二培频交流分量指数衰减常数。

转子绕组中的电流为

if=if[0]+

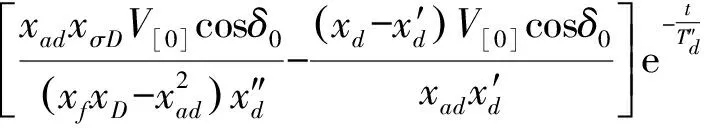
(3)

式(3)中:xD,xQ分别为d轴，q轴阻尼绕组的电抗；xad，xaq分别为发电机转子纵轴、横轴电抗；xσD,xσQ分别为d轴，q轴定子绕组漏电抗；xf为励磁绕组电抗。

1.2 短路故障仿真模型

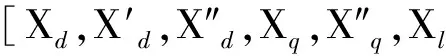
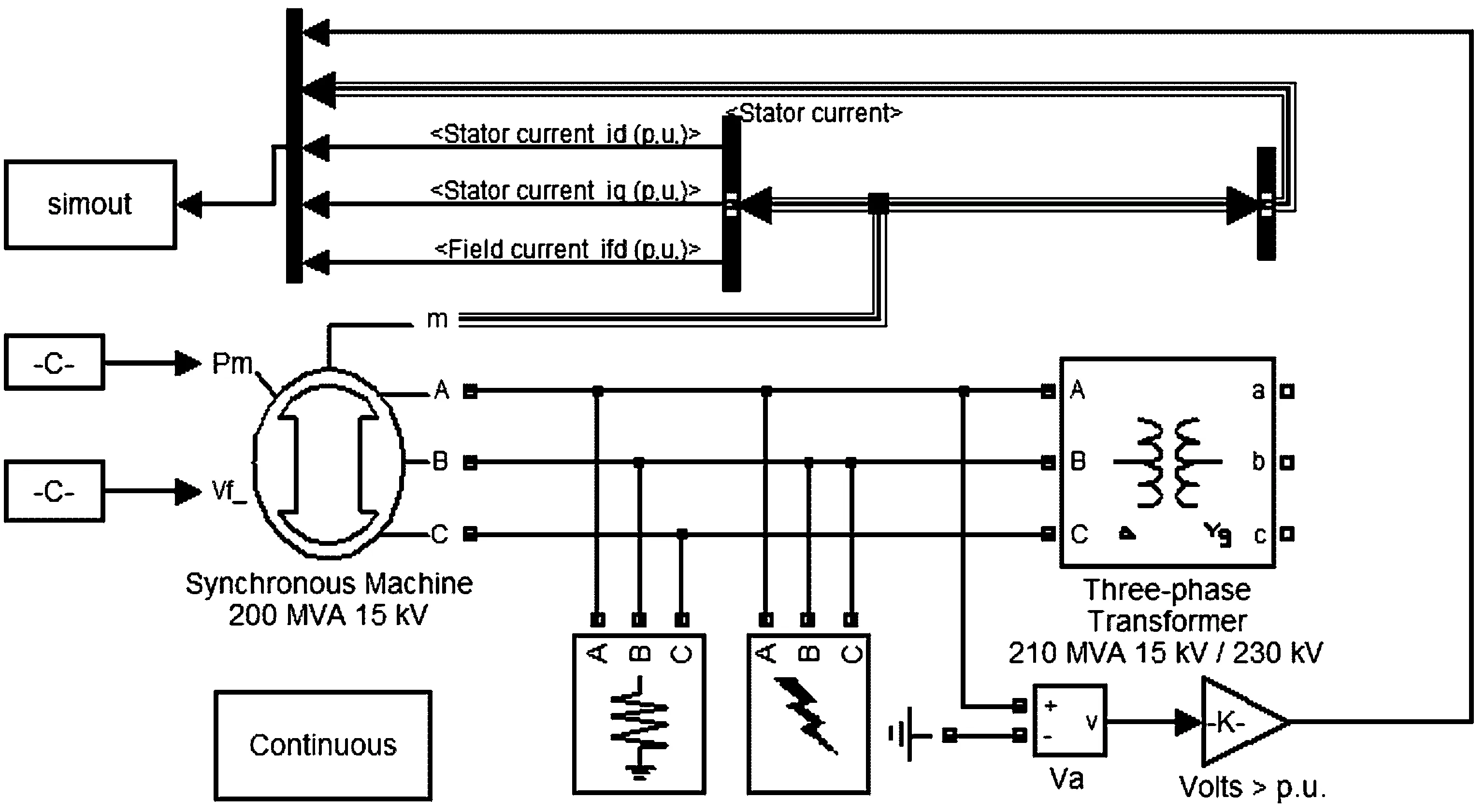
图1 同步发电机短路故障仿真模型

得到a相正常，b、c两相同时短路的定子电流变化情况如图 2所示，可知定子的a相电流波动幅值较小，在±0.05 p.u.之间，在0.02 s之前为正常状态，幅值较0.02 s后出现故障时的幅值较小。在发生故障时，b相和c相电流发生迅速且剧烈的振荡，波动幅值在±5.0 p.u.之间，并伴随有近似指数规律的衰减趋势。因此在a相正常，b、c两相同时短路时，定子的a相电流波动变化较小，而b、c两相电流较大，明显不正常。

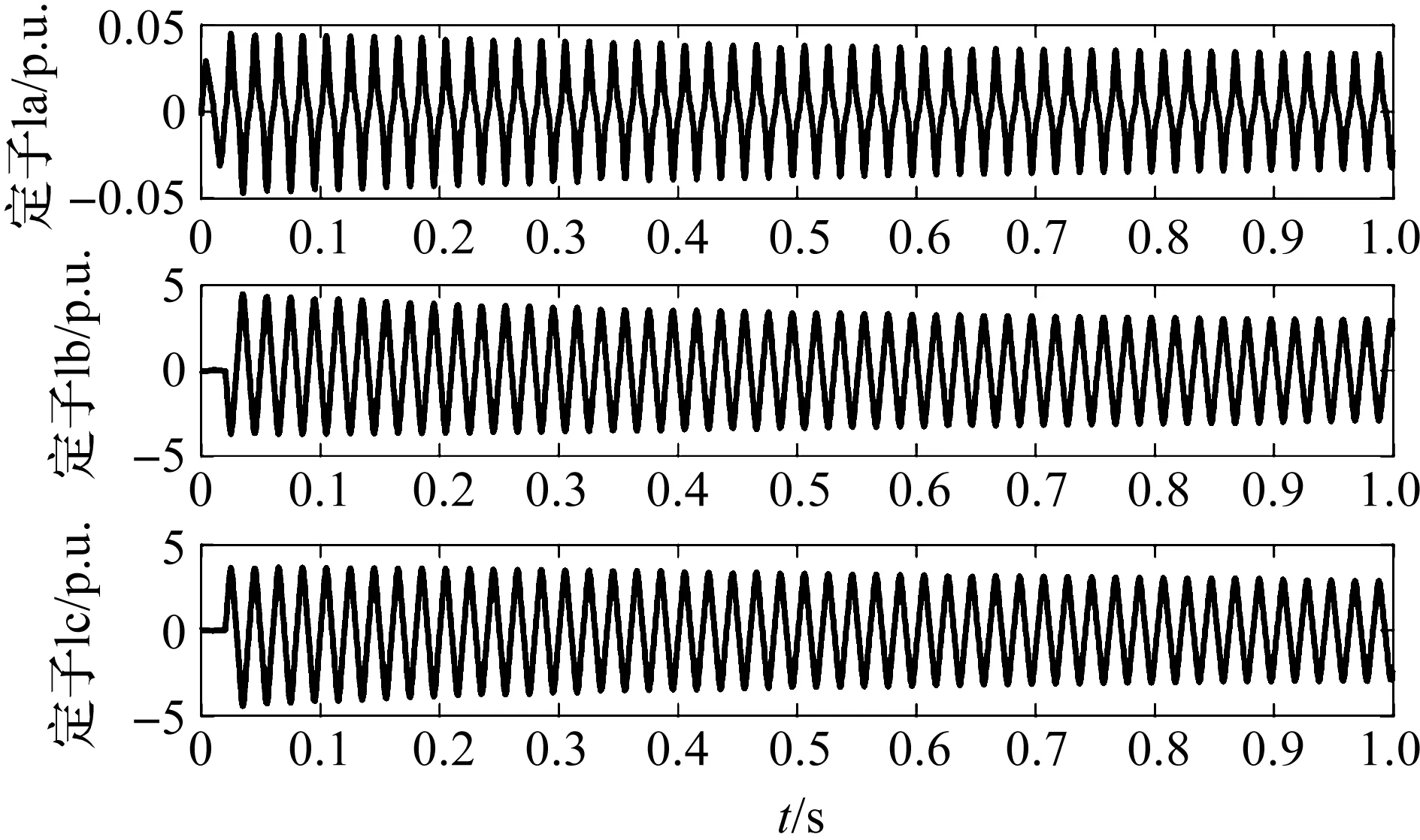
图2 a相正常，b、c两相同时短路电流变化

得到b相正常，a、c两相同时短路的定子电流变化情况如图 3所示，可知定子的b相电流波动幅值较小，在±0.5 p.u.之间，在0.02 s之前为正常状态，幅值较0.02 s后出现故障时的幅值较小。在发生故障时，a相和c相电流发生迅速且剧烈的振荡，波动幅值在±10.0 p.u.之间，并伴随有近似指数规律的衰减趋势，两者的变化具有对称性。因此在b相正常，a、c两相同时短路时，定子的b相电流波动变化较小，而a、c两相电流明显不正常。

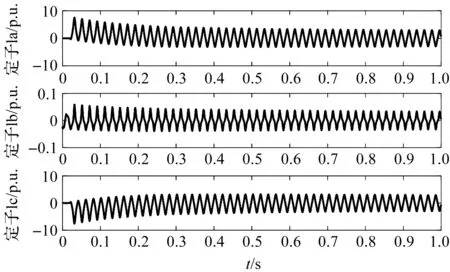
图3 b相正常，a、c两相同时短路电流变化

得到c相正常，a、b两相同时短路的定子电流变化情况如图 4所示，可知定子的c相电流波动幅值较小，在±0.5 p.u.之间，较正常状态下的电流有所增大，在0.02 s之前为正常状态，幅值较0.02 s后出现故障时的幅值较小。在发生故障时，a相和b相电流发生迅速且剧烈的振荡，波动幅值在±10.0 p.u.之间，并伴随有近似指数规律的衰减趋势，两者的变化具有对称性，因此在c相正常，a、b两相同时短路时，定子的c相电流波动变化较小，而a、b两相电流明显不正常。

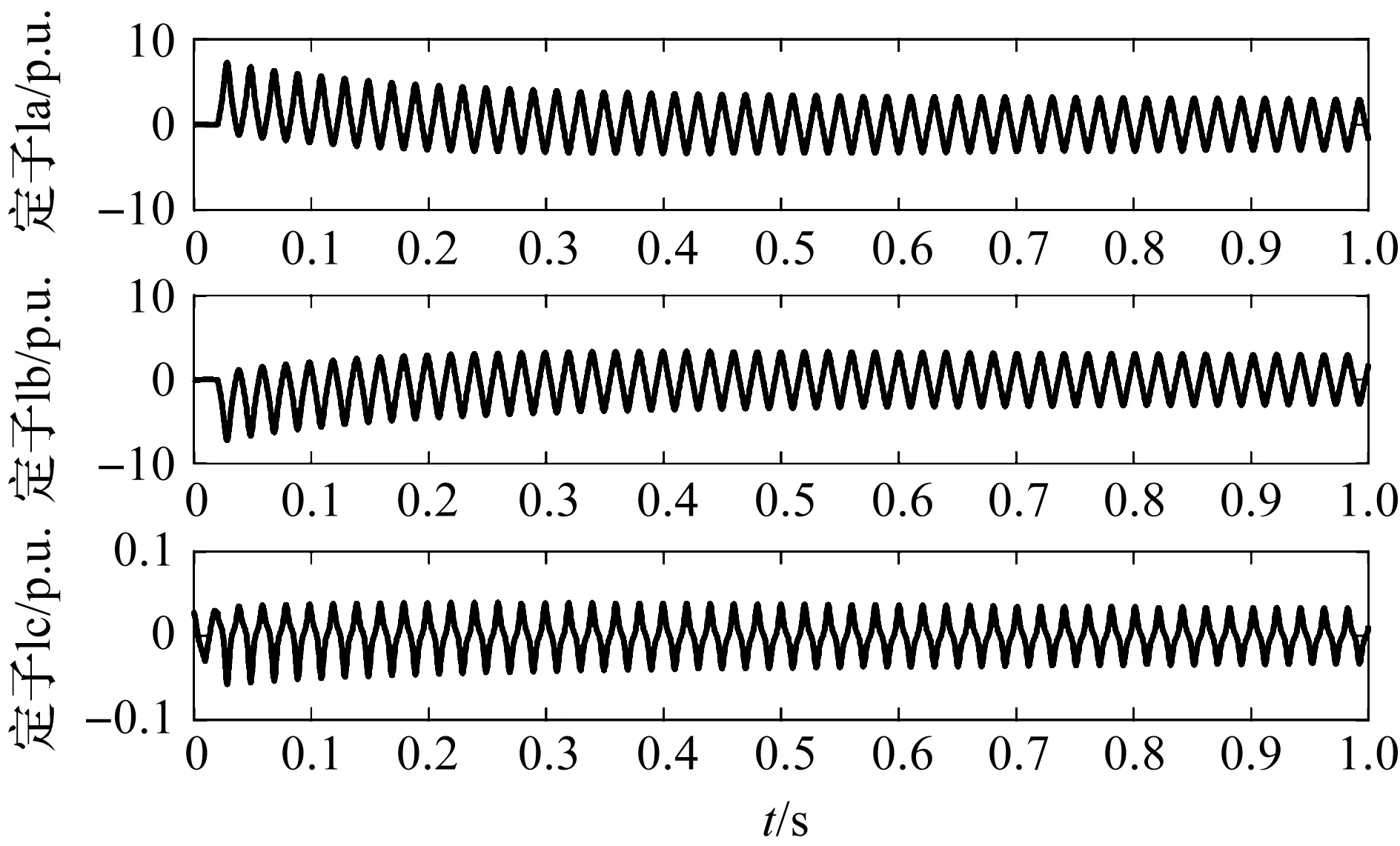
图4 c相正常，a、b两相同时短路电流变化

得到a相短路，b、c两相正常的定子电流变化情况如图 5所示，可知定子的三相电流均处于较小幅值的波动状态，在单相故障产生时并没有发生明显的电流增大且剧烈波动现象。

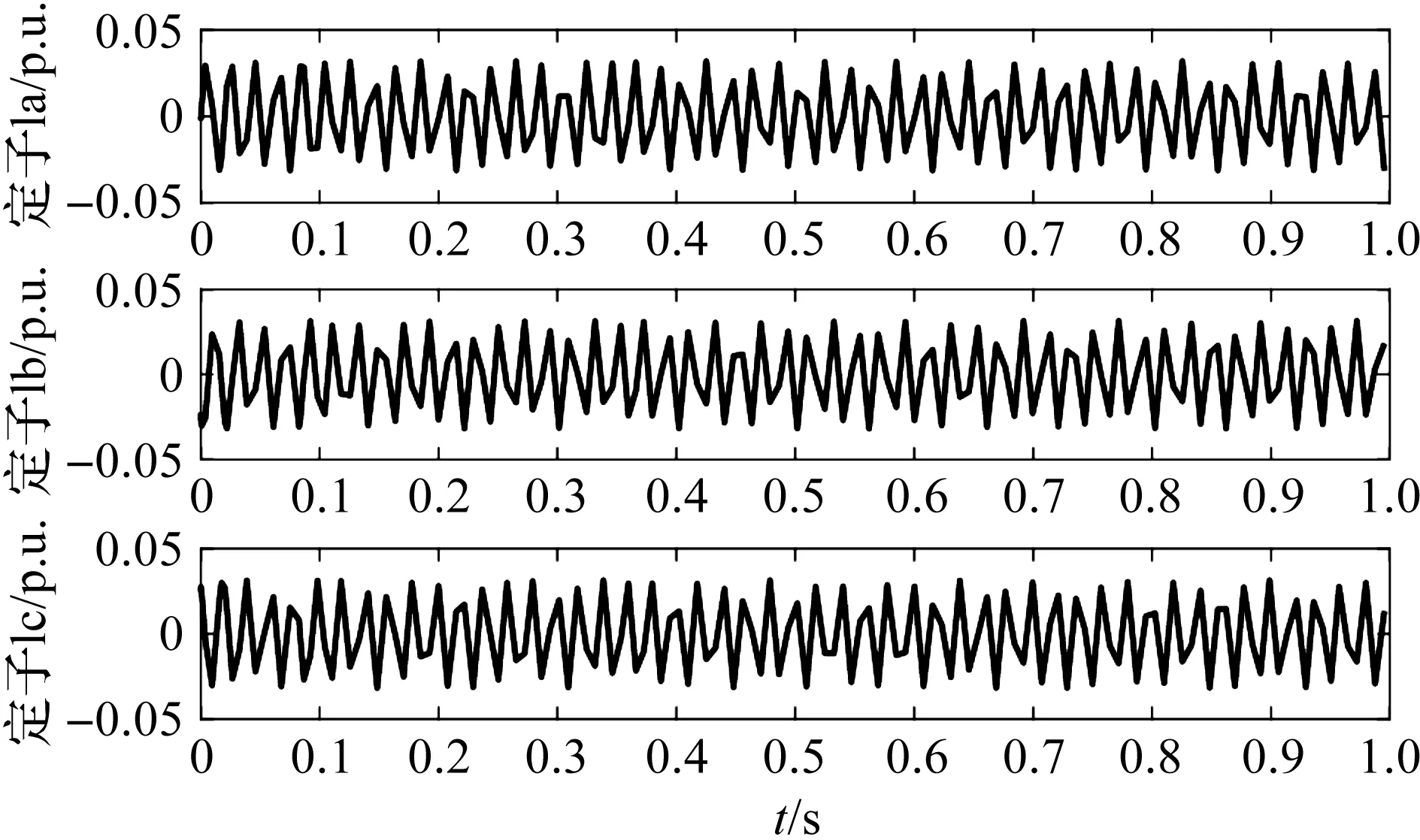
图5 a相短路，b、c两相正常的电流变化

同理，可得同步电机未发生短路故障时的电流变化，及剩余的3种短路故障时定子电流变化情况，包括b相短路，a、c两相正常；c相短路，a、b两相正常；a、b、c三相短路。

2 BP网络与反向传播算法

对一个单层神经网络，其第i个神经元的实际输出为

(4)

式(4)中：ai为第i个神经元的实际输出；pj为输入p的第j个输入；ωij为第i个神经元的输入p的第j个输入权值；bi为第i个神经元的偏置值。

根据基本神经元计算方法，一个典型的多层神经网络拓扑结构图如图6所示(图中为一个3层神经网络，BP网络一般设置3层即可满足大部分工程应用)，根据拓扑结构图可得网络的输出与输入间的关系为

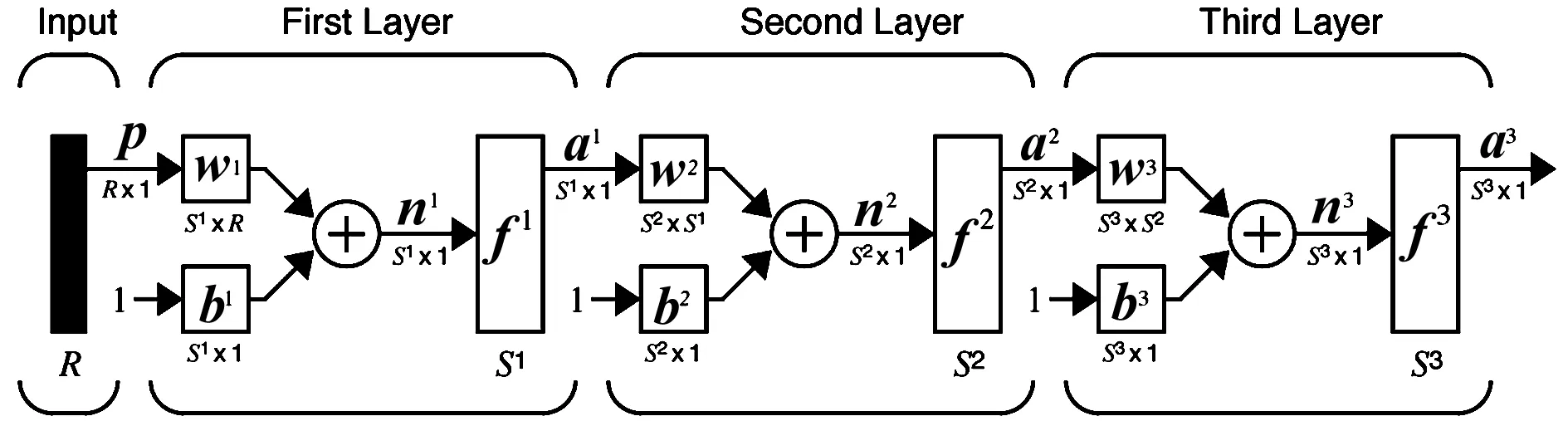
图6 多层神经网络

a3=f3(w3f2(w2f1(w1p+b1)+b2)+b3)

(5)

式(5)中：a3为网络的第3层输出；f1，f2，f3分别为网络的第1，2，3层的激励函数；w1，w2，w3分别为网络的第1，2，3层的权值矩阵；b1，b2，b3分别为网络的第1，2，3层的偏置矩阵。

设计均方误差函数为

F=(t(k)-a(k))T(t(k)-a(k))=eT(k)e(k)

(6)

式(6)中：t(k)为第k个神经元理想输出向量；a(k)为第k个神经元实际输出向量;e(k)是期望值t与实际输出值a的差。

将式(5)对网络的权值和偏执值进行求偏导，可得

(7)

式(7)中：ωij为第i个神经元的输入p的第j个输入权值；pj为输入p的第j个输入。

将有监督的Hebb学习规则应用到网络的权值和偏置值的迭代更新中，可得基于最小均方误差算法的权值与偏执值的更新公式为

(8)

式(8)中：α为学习率；p为输入向量。

定义网络的m层，第i个神经元敏感度为

(9)

根据导数的链式法则，求导过程为

(10)

由式(6)和式(9)，得到敏感度的反向传播的递归关系为

(11)

由式(10)可知，反向传播网络当前层的敏感度值由后一层的敏感度确定，这是反向传播神经网络算法的最大特点。

根据式(10)可得BP神经网络的权值与偏执值的反向传播更新公式可表示为

(12)

由式(5)和式(12)可知:神经网络的激励函数、学习率和偏置值是3个重要组成部分，而神经元的激励函数选择不同将会产生不同功能的网络，对BP神经网络来说，在工程上常用Sigmoid函数作为BP网络神经元的激励函数，在神经网络中亦使用Sigmoid函数，其表达式为

(13)

3 基于BP网络的同步发电机短路故障模式识别

由定子电流数据可知，BP网络的输入层神经元个数为3；设置隐含层神经元数量为10个；根据模式识别的故障种类可知共8种模式类别，因此可设置网络输出层的神经元数量为8个，8个输出组成一个向量，向量的第i个元素代表第i种故障模式，如表 1所示。由Sigmoid函数可知每个故障模式的输出范围均为[0,1]，若识别得出为无故障模式，则输出向量第1位的值应最大。

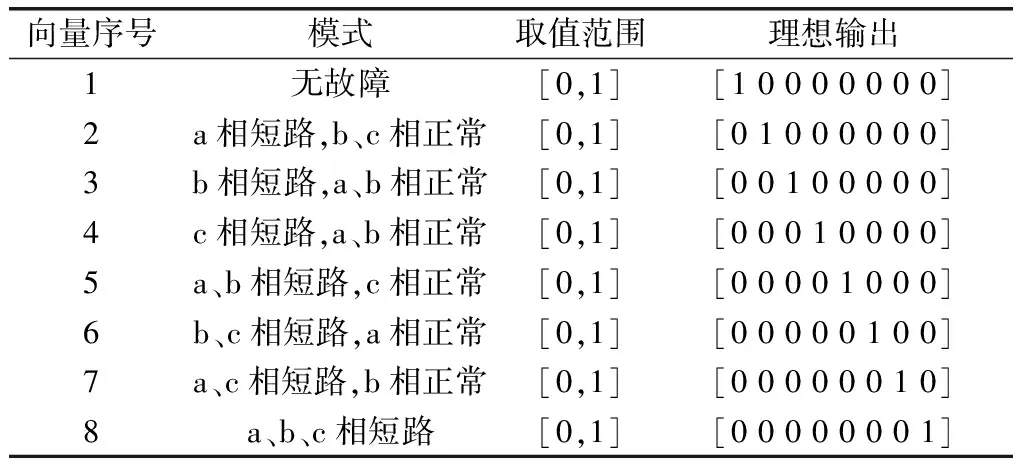
表1 输出向量对应故障模式表

设置BP网络最大迭代次数为2 000次，训练目标误差0.01。根据设计目的，将0～0.02 s时间内的仿真数据作为无故障模式输入数据，数据点共6个；将0.02～0.8 s时间内的仿真数据分别作为网络的训练数据，数据点共108个，得到经过训练后的BP网络模式识别器，此时网络的权值和偏置值完成迭代计算；将0.8～1.0 s时间内的仿真数据分别作为网络的测试数据，数据点共24个，为弥补单点测试结果的误判，提高诊断的准确率，以一段时间内的多个数据作为测试对象，以测试结果的平均值作为最终诊断结果，去除测试结果中的最大值和最小值，得到结果向量为

(14)

式(14)中:Rj为测试结果第j个元素值；Tj为测试结果向量的第j个元素值；Tjmax为测试结果向量的第j个元素的最大值；Tjmin为测试结果向量的第j个元素的最小值；R为测试结果向量。

得到训练后的模式识别器测试结果如图 7所示，图中横坐标1～8分别表示如表 1所示的8种故障模式，纵坐标为由训练后的BP网络模式识别器计算得到的数值(无单位)，可知模式识别器很好地识别了8种模式的测试数据，单点数据诊断的准确率均大于95%，说明识别器的训练效果良好，每种模式的识别结果平均值均大于0.8，虽然较相似的故障模式的平均值较相近，但数值均小于0.5，如对模式1进行诊断，得到模式2～模式4的诊断结果与模式1相近，但数值差别较大，并不影响最终结果的判断。由测试结果可知，识别器对故障模式诊断的准确率为100%，这得益于多数据点识别并求平均值的算法，有效地规避了单数据点识别的偶然性，提高了识别的准确率。

4 结 语

以上分析通过建立同步发电机短路故障数学模型，给出定子d轴和q轴的电流分量、相电流和转子绕组电流的计算公式。在MATLAB Simulink中搭建了15 kV，50 Hz，200 MV·A同步发电机MATLAB短路故障仿真模型，得到8种短路故障时的电子电流变化数据，通过建立BP神经网络模型及多数据点求平均值故障识别算法，以短路故障定子电流变化的80%数据量作为BP网络的训练输入，以剩余电流变化的数据进行多数据点故障识别测试，得到故障模式测试结果，提高了BP网络模式识别器的准确率，为基于BP神经网络的同步发电机短路故障模式识别研究提供了参考。