基于MATLAB的受控PWM电压H桥直流电机控制与仿真

张文正

( 安徽三联学院 基础实验教学中心，安徽 合肥 230601)

直流电机是向负载提供转动和扭矩的执行机构，将直流电能转化为旋转运动的机械能，其转子或电枢所产生的扭矩绝大部分用于驱动外部载荷[1-3]，由于具有扭矩大、速度可控范围宽、便于携带、适应性强等优点，在机器人操作系统、机床，以及伺服系统、磁盘驱动器、传输系统等实际控制系统中应用广泛。由于直流电机的驱动功率仅与输入电压和电流有关，对其进行功率或转速控制的方法也较为简单。目前，常采用脉冲宽度调制(PWM，Pulse width modulation)的方法实现对直流电机电压或电流的控制，因此国内外学者对PWM控制系统的研究非常多[4-7]。王子权[8]为实现节能型LED灯的亮度与功率控制，使用STM32F103ZET6型单片机设计制作了简单易操作和节能高效的调光器，通过对PWM调制基本原理的分析，对从电位器输入的数据进行了处理，得到脉冲宽度调制的占空比,并通过开发部设计1 000级LED灯亮暗调节装置。结果表明，LED灯虽然具有平滑的亮暗变化，但由于其使用的试验装置仅仅是对单片机引脚的PWM控制，因此控制功率和效率不高，无法应用在较大功率脉宽调制控制场合。Mousavizadeh等[9]提出了一种基于后向-前向扫描(BFS)算法的交直流配电网潮流分析新方法，该方法应用Clarke变换对不平衡运行条件下脉宽调制(PWM)变换器的运行进行建模，模型考虑了不同的控制策略，包括输入功率控制(IPC)、输入输出功率控制(IOPC)和输出功率控制(OPC)，通过仿真结果得出模型在不平衡交直流配电网潮流分析中的有效性和适用性。为了增强PWM控制直流电机的适用范围，提高控制功率，可搭建受控PWM电压H桥控制方法，该方法只需对PWM的参考电压进行控制，通过H桥模型后直接驱动直流电机，H桥通常采用MOSFET开关配合相关的控制芯片实现。若将参考电压描述为一个阶跃激励信号，机电系统控制原理分析，让某个被控构件突然运行到某个量是不合理的，这会导致某些物理量的速度或加速度变化过快(如位移、力、力矩等)，因此需对激励信号进行控制[10-13]。韩京清等[14-15]提出了二阶离散系统最速控制综合函数，从而构造出了离散形式的微分跟踪器，通过数值仿真表明跟踪器可快速、无超调、无震颤地跟踪输入信号，并将跟踪器应用于非线性自抗扰PID控制器，给出了高品质的新型控制器，因此该微分跟踪器可作为对参考电压信号的过渡和跟踪，从而控制受控PWM电压的阶跃激励时间和响应幅度。

笔者基于MATLAB Simulink建立受控PWM电压H桥直流电机控制与仿真模型；分析直流电机系统控制模型，给出其一般性传递函数；分析PWM的基本原理，给出其输出电压与占空比的关系函数；给出直流电机H桥硬件电路模型，为H桥控制器的搭建提供参考；建立阶跃型激励信号的微分过渡算法，为受控PWM电压H桥直流电机高精度控制系统设计与实现提供参考；介绍模型的构件过程及仿真流程，得到符合实际的电机电流和转速平滑过渡变化曲线。

1 直流电机控制系统

1.1 直流电机控制模型

直流电机模型如图1所示，常用的永磁电枢控制式直流电机控制模型组成包括励磁系统、电枢和负载，将直流电机进行线性处理，忽略磁滞现象和电刷上的压降等因素，以电枢电流Ia为控制变量，电机的扭矩为

图1 永磁电枢控制式直流电机

Tm(s)=KmIa(s)

(1)

式(1)中：Km为永磁体材料的磁导率,H/m；Ia为电枢电流,A。

电枢电流与作用在电枢上的输入电压之间的关系为

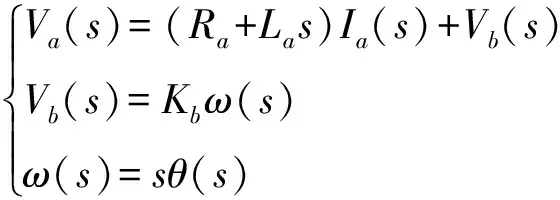
(2)

式(2)中：Va为电枢输入电压，V；Ra为电枢电阻，Ω；La为电枢电感，H；Vb为与电机速度成正比的反相感应电压，V；Kb为电机转速比例系数；ω为电机实际转速，rad/min；θ为电机角位移,rad。

联立式(1)～式(2)可得电枢电流为

(3)

根据牛顿-欧拉力学定理，可得电机负载扭矩为

TL(s)=Js2θ(s)+bsθ(s)

(4)

式(4)中:J为负载的转动惯量,kg·m2；b为负载的摩擦系数。

联立式(1)～式(4)可得直流电机传递函数为

(5)

式(5)中：ωn为固有频率；ξ为系统阻尼。

式(5)即为永磁电枢控制式直流电机的一般控制模型。若忽略电枢的时间常数τa=La/Ra，可得

(6)

1.2 PWM控制原理

PWM是一种信号周期一定而高低信号的占空比可调的方波信号[16-17]，其脉宽调制图如图2所示。PWM信号的实质就是调节占空比来改变负载两端的电压平均值，即

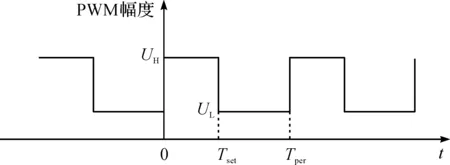
图2 PWM脉宽调制图

(7)

式(7)中：UH为PWM高电平电压值,V；UL为PWM低电平电压值,V；Tset为PWM高电平时间,s；Tper为PWM的周期,s；k为PWM周期次数。

由式(7)可得PWM波输出电压平均值为

Uavr=α(UH-UL)+UL,(0≤α≤1)

(8)

式(8)中α为PWM脉宽调制的占空比。

根据功率守恒定律，可得PWM输出的平均电压Uavr与直流电机转速之间的关系为

(9)

式(9)中ωe为电机空载转速, rad/min。

1.3 基于MOSFET的H桥电路设计

如图 3所示为一种MOSFET 12 V电压控制H桥电路，该电路可实现两路PWM控制(PWM1_IN和PWM2_IN),从而可对直流电机进行正转和反转控制。图中Q1～Q4即为场效应管，PWM波形通过控制场效应管通断实现直流电机通断，场效应管的通断时长与PWM波形的占空比一致。图中EG2104为半桥驱动芯片，两个EG2104对称组合布置即可完成整桥驱动。图中1N4184二极管即为高频开关电路中的续流二极管，利用其单向导通作用，在H桥驱动电路中起到保护和稳定输入输出的功能。图中的J1B即为连接直流电机正极和负极的引脚，由于直流电机本身的特性，可无需区分正负极连接。

图3 MOSFET的H桥硬件电路

1.4 基于微分跟踪器的信号过渡算法

在控制系统设计时，激励信号的微分偏差较大时(如阶跃激励信号)，让执行机构或某些物理量突然运动或变化到某一状态是不合理的，因此通常的做法是使用余弦信号让执行机构或某些物理量运动的速度或加速度平滑连续变化。而在某些控制系统中，阶跃激励信号并不能完美地解决系统迟滞和响应速度慢的问题，且阶跃激励信号无法控制系统的响应时间。为此，需建立某种控制算法，该算法即可使缓慢平滑过渡微分偏差较大的信号，有可通过调整参数的方式实现过渡信号的时间控制。参考自抗扰PID控制算法，其微分跟踪器模块可实现上述功能，并可同时实现一定的噪声过滤功能。

微分跟踪器的数学描述为

r1(k+1)=r1(k)+hr2(k)
r2(k+1)=r2(k)+
hf(r1(k)-yd(k),r2(k),δ,h)

(10)

式(10)中：h和δ为跟踪器控制变量，通过改变控制变量值实现过渡信号的调整；f为最速控制综合函数；yd(k)为第k时刻的输入信号；r1(k)为输入信号的跟踪信号；r2(k)为输入信号的速度跟踪信号。

令状态变量x1=r1(k)-yd(k)，x2=r2(k)，得到最速综合控制函数表达式为

式(1)中a为符号函数变量，其表达式为

(12)

根据微分跟踪器控制算法，对幅值为3的阶跃信号，通过调整控制变量h和δ分别为(0.01，50)，(0.01，5)，(0.01，1)，(0.01，0.7)，(0.01，0.5)，(0.01，0.2)，并将过渡时间控制为4 s，在MATLAB中进行总时间10 s的仿真计算，得到阶跃输入信号和过渡信号如图 4所示。从图4中可以看出：当h=0.01和δ=0.7时，满足微分过渡时间控制要求，同时由于微分过渡算法的引用，控制信号由原来的阶跃型激励变为了能够平滑变化的过渡信号，这对改善控制系统有一定好处。

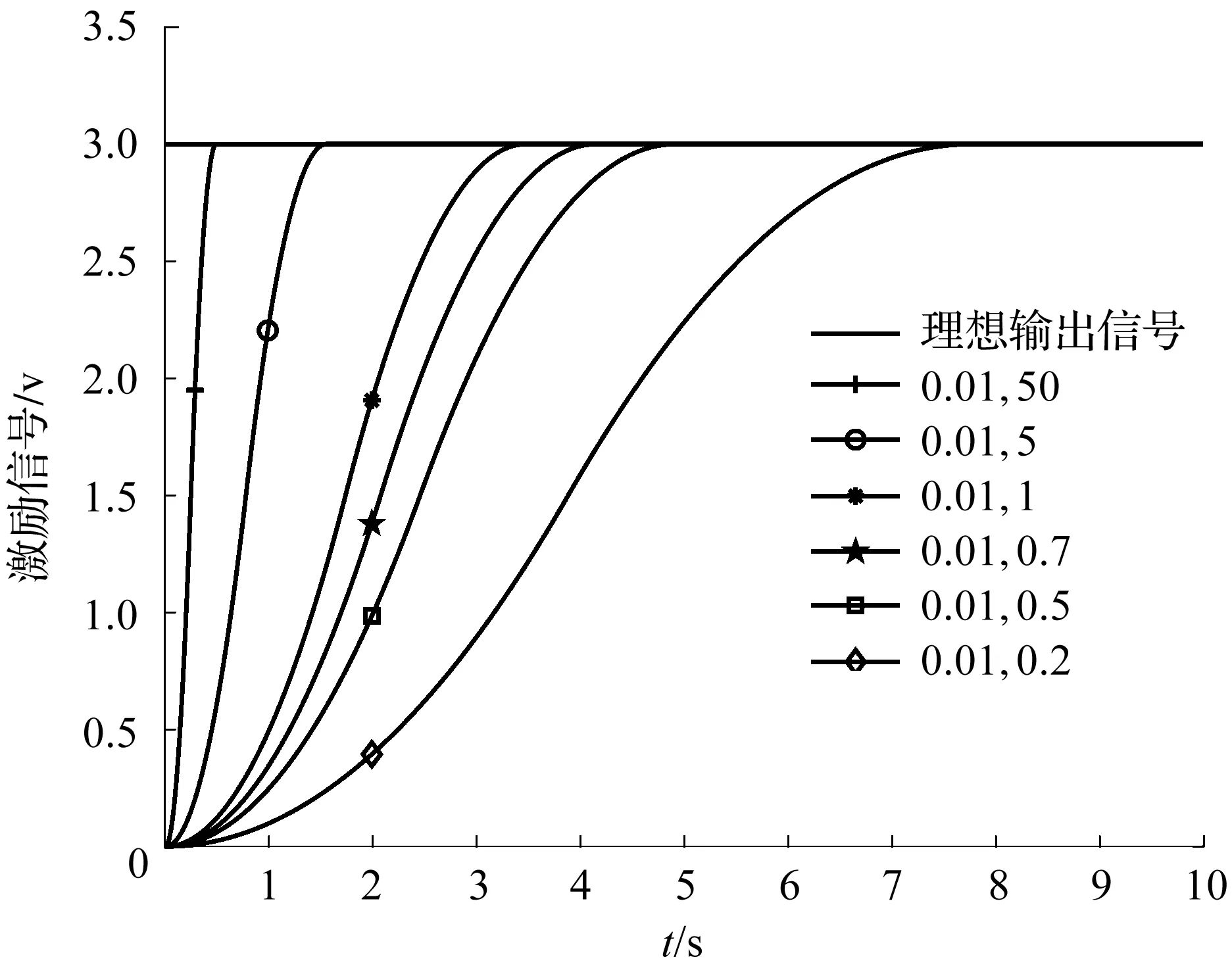
图4 微分跟踪过渡过程仿真结果

2 基于MATLAB的控制模型设计与仿真分析

2.1 控制模型设计

在MATLAB Simulink中设计控制模型，设计参考电压值范围为0～5 V，PWM受控电压范围为0～5 V，H桥输出电压为0～12 V，以驱动额定电压为12 V的直流电机，如图 5所示。图5中的参考电压值设定为微分跟踪过渡信号，受控PWM电压模块设置：PWM波频率为4 000 Hz，占空比为1时的输入电压为5 V，占空比为0时的输入电压为0 V，PWM波形输出电压幅值为0～5 V。H桥模块设置：PWM信号最大值为5 V，输出电压最大值为12 V，等效电阻为0.1 Ω，续流二极管导通电阻为0.1 Ω。直流电机模块设置：电枢电感为0.01 H，空载转速为4 000 rad/min，额定负载下的额定转速为2 500 rad/min，额定功率为10 W，额定电压为12 V，转子惯性0.000 2 kg/m2，初始转速为0 rad/min。

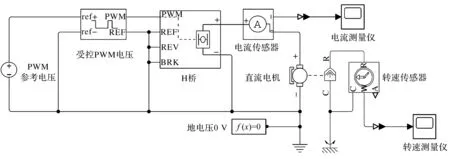
图5 基于MATLAB的控制模型

仿真模型计算流程框图如图6所示。根据设计要求进行信号的微分跟踪计算，将计算得到的信号序列导入参考电压模块，受控PWM电压模块在获得参考电压后即进行控制操作，直至直流电机达到控制转速。按笔者微分跟踪器的设计，参考电压为3 V，因此可知电机的稳态转速为2 400 rad/min，过渡时间控制为4 s，仿真总时间为10 s。

图6 控制模型仿真流程

2.2 仿真结果分析

直流电机的控制电流如图 7所示。由图7可知,直流电机在启动瞬间电流值最大，达2.080 8 A，这与实际情况符合，因为电机在启动瞬时，电机并未立即产生转速，将电能转化为机械能，此时的电能主要用于电机本身的电气特性中，导致启动电流较大。

图7 控制电流仿真结果

随着时间的推移，电流值逐渐减小，呈明显的指数下降趋势，这与实际情况是符合的。当时间为4 s时，电机上的电流逐渐趋于稳态，稳态值为0.045 A，这与微分跟踪器设计的4 s稳态时间是相符合的，同时可以看出由于微分跟踪器的存在，电流的下降过程十分平滑。

直流电机的控制转速如图 8所示。由图8可知,直流电机在启动的瞬间转速为0，电机无机械能输出，从而可知此时的电机电流较大，这与图 7的仿真结果相对应，符合实际情况。随着时间的推移，电机的转速逐渐增大，呈明显的指数上升趋势，这与实际情况是符合的。当时间为4 s时，电机转速逐渐趋于稳态，这与微分跟踪器设计的4 s稳态时间是相符合的，同时可以看出由于微分跟踪器的存在，电机转速的上升过程十分平滑，电机转速的稳态值为2 398.5 rad/min，与理论稳态值2 400 rad/min十分接近，达到了较高的控制精度。

图8 控制转速仿真结果

3 结 语

笔者分析了直流电机系统模型，给出了永磁电枢控制式直流电机一般性传递函数和忽略电枢的时间常数的传递函数，为直流电机控制系统设计提供了参考；分析了PWM的基本原理，给出其输出电压与占空比的关系函数和参考电压与直流电机空载转速的计算公式；设计分析了一种直流电机正反转H桥控制硬件电路模型；建立的阶跃型激励信号的微分过渡算法，为受控制系统信号平滑过渡提供了理论依据。经MATLAB Simulink仿真计算得到的电机电流和转轴变化结果，可知微分跟踪器很好地实现了阶跃型激励信号的平滑过渡，且控制器达到了较高的控制精度。