超声速三维空腔流气动噪声被动控制
2022-08-11冯峰,王强
冯 峰,王 强
(中国航天空气动力技术研究院,北京 100074)
引 言
先进军用飞机,如我国J-20,美国猛禽F-22、闪电Ⅱ F-35战斗机和幽灵B-2轰炸机等,为了飞行隐蔽性和减小飞机阻力均采用了内埋式武器舱设计。然而,超声速内埋武器舱空腔流产生的声-流共振现象及恶劣噪声环境能够影响武器的安全投放和舱内设备疲劳寿命。随着战斗机、轰炸机内埋武器舱设计的广泛使用,超声速空腔流噪声预测和控制成为长期需面对的问题。
空腔流声-流共振及噪声效应在20世纪50年代开始成为备受关注的热点课题[1-2]。空腔流声-流共振的机制在于声反馈环,其形成原因通常认为是自由来流与腔内空气混合形成剪切层流动,受Kelvin-Helmholtz不稳定性主导,不稳定扰动波在剪切层内增长促使其发展形成高度有序的大尺度涡列结构。涡列与空腔后壁撞击产生反射的压力波经腔内向前传播,激励空腔前缘初始剪切层流动,迫使剪切层不稳定性增强并诱导涡列卷起。当不稳定扰动波与反射压力波频率相匹配时,空腔内出现流场-声场相互耦合的声反馈环现象,即形成该特征频率主导的声-流共振现象和强噪声环境。
目前已发展出大量抑制空腔流声反馈环的流动控制技术。Rowley等[3]对相关控制技术进行了详细归纳,并将其分为主动、被动两大类。被动控制技术包括:锯齿形扰动装置[4]、扰动圆杆[5]、静止/振动扰动片[5-6]、前缘斜坡[7]等。这些装置均有一定的降噪效果,但大多数只在某一特定范围流动条件下才能发挥作用,且经常会引起一些副作用,如增加飞行器阻力等。最近,一些主动控制技术也被不断开发出来,如Vakili等[8]发展的吹气扰动降噪技术,以及Stanek等[9]展示的主动共鸣管装置等,都可以根据当前流动情况调整扰流强度达到降低空腔流噪声的目的。其中Zhuang等[10]在空腔前缘采用超声速微喷流主动控制技术能够产生明显的流向涡,利用其弱化混合层速度梯度并增加混合层厚度的机制[11],显著抑制了腔内非定常流动并降低整体声压级(overall sound pressure level,OASPL)达9 dB。但主动控制技术大多需引入相当大质量的控制装置,长期使用可能导致装置疲劳及工作性能下降的问题,在实际应用中难以推广。客观上,高效地控制空腔流动及噪声目前仍难以实现,一方面空腔流动对外部扰动十分敏感,另一方面建立精确的控制系统也十分困难。受军事航空领域应用需求牵引,仍需不断深入探索和改进空腔流动噪声控制技术。
近年来,利用高精度数值方法开展空腔噪声控制机制的研究得到蓬勃发展。如Dudley等[12]采用大涡模拟(large eddy simulation,LES)方法计算分析了扰动圆杆被动控制技术对空腔流噪声的抑制作用和机制,Zhang等[13]采用分离涡模拟(deta-ched-eddy simulation,DES)方法研究了定常微吹气主动控制技术对空腔流的降噪效果和机制,均展现出数值方法探索空腔噪声控制机理的巨大潜力。为提升对空腔流被动噪声控制技术机制的理解,并实现对腔内噪声的有效控制,本文利用LES技术计算分析了Mach 1.4矩形方腔及弧形、波形两种空腔前后壁几何修形的流动及噪声环境,探索在超声速来流条件下几何修形被动控制技术对舱内噪声的控制机制和效果。此外,还应用LES方法初步研究分析了增厚的来流入口边界层对超声速方腔腔内的噪声影响,确定来流边界层厚度对空腔流噪声的控制效果。
1 数值方法
1.1 控制方程
控制方程为可压缩完全气体Navier-Stokes的空间滤波方程,简化形式如下
(1)
(2)
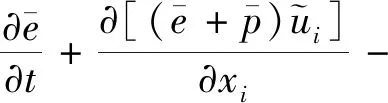
(3)
上述方程组采用来流密度、来流声速、空腔深度等作为特征参考量进行无量纲化。并导出来流Mach数、Reynolds数和Prandtl数等无量纲参量。本文分别设定为Ma=1.4,Re=10 000,Pr=0.71。为使方程(1)~(3)封闭,增加一个完全气体状态方程
(4)
式中,比热比γ=1.4。方程(1)~(3)中SGS应力张量通过Smagorinsky模型建模,形式为
(5)
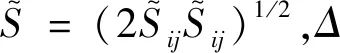
(6)
其中,CS,CI是Smagorinsky模型系数,Prt是湍流Prandtl数,设定CS=0.012,CI=0.006 6,Prt=0.9。
1.2 计算方法
声的产生及传播对空腔流声-流耦合振荡的形成和发展十分重要,本文选用高精度气动声学计算格式对控制方程进行离散。空间格式使用Tam等[14-15]提出的7点4阶色散关系保持格式,时间推进采用了Berland等[16]发展的适应于非线性问题的优化低存储6步4阶Runge-Kutta格式。计算中引入人工选择性阻尼项对非物理短波滤波[14-15]。选择性阻尼项、黏性项及SGS项均只在Runge-Kutta最后一个子步中被求解。LES计算采用Bogey等[17]的自适应空间滤波法捕捉激波间断并维持湍流脉动求解稳健性。

图1为标准矩形空腔模型的网格设置,共约 9×106个网格点求解空腔流及噪声。方腔长深比L/D=6,宽深比W/D=2。计算域范围为x1=-3~13,x2=-1~9,x3=-2.5~2.5。空腔内采用了199×103×91个Cartesian网格点,空腔外计算域采用了339×141×183个网格点。在壁面附近对网格进行了加密,最终各方向上最小网格尺度为Δx1=0.002,Δx2=0.001,Δx3=0.002。LES计算均执行 5×105次迭代,时间步长Δt=0.000 5,流场统计均在105步后启动。为加速计算,采用MPI并行代码,每次计算使用84个进程,一次计算约花费480 h。
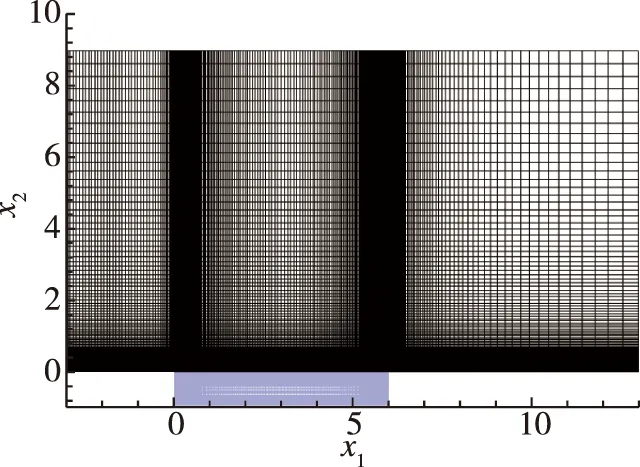
(a) x1-x2 cross section(x3=0)
图2展示了3种空腔几何构型的俯视图,按照外形特征分别称为标准矩形方腔、波形空腔和弧形空腔。波形和弧形空腔前后壁展向形状采用余弦函数生成
w(x)=A·cos(Bx3/W)
(7)

(a) Rectangle cavity
其中,w为展向形状函数。A为余弦波幅值,波形空腔A=0.25,弧型空腔A=0.5。B控制余弦波数,波形空腔B=2.5,弧形空腔B=0.25。3个空腔宽度、深度相等,均满足W/D=2。空腔前后壁同时采用余弦函数外形,每个流向位置处长深比都为L/D=6,即3个空腔的容积率相同。
1.3 数值验证
图3是本文LES计算与Dudley等[12]的实验获得的方腔典型位置x3=0截面上空腔流时均流向速度云图。对比表明二者展现的时均流向速度形态及空间分布等完全一致,均体现出了明显的剪切流动特征,即方腔上方剪切层沿下游逐渐增厚,受方腔后壁遮挡而浸入腔内的流动现象,空腔前部及底部平均流向速度相对较低。

(a) LES:
进一步地,图4定量对比了方腔x3=0截面x1=3流向站位上LES与Dudley等[12]实验测量及DES计算结果获得的时均流向速度型和流向脉动速度均方根。由图可见,LES计算结果与实验测量及文献DES计算结果很好地吻合,能够精确定量刻画剪切层及空腔内流向速度和时均湍流速度大梯度变化的特征,证明本文LES数值方法具有准确捕捉剪切层和方腔湍流能力。

(a)
2 几何修形对空腔噪声影响
2.1 空腔流动及噪声对比
图5展示了弧形、波形两种空腔流在x3=0截面上时均流向速度云图。与图3标准矩形方腔流相比,几何修形空腔流动的初始剪切层发展与其基本一致,但在空腔后部的演化形成较大差异。具体而言,矩形方腔剪切层后期演化向腔内扩展区域最小,弧型空腔剪切层占据空腔后部区域最大且剪切层发展最为饱满。而波形空腔剪切层在空腔后部扩展的区域相对增大,临近空腔底壁面存在范围较大且较明显的低速区。时均流向速度展示了空腔几何修形能够控制剪切层及腔内流动的演化特性。

(a) Curved cavity:
图6给出了3种空腔在x3=0截面上展示湍流脉动强度的流向(x1)、法向(x2)和展向(x3)速度脉动均方根云图。由图可见,3种空腔均在后半腔及剪切层内呈现出显著的湍流脉动。流向、法向和展向速度脉动均方根一致显示弧形空腔内湍流脉动弱于矩形方腔,波形空腔内湍流脉动强度又弱于弧形空腔。从流向速度脉动均方根观察,3种空腔在剪切层发展初期湍流脉动强度较为接近,但在空腔下游,几何修形明显降低了腔内流动振荡导致的湍流脉动强度。法向和展向速度脉动均方根也能够很好展示几何修形对空腔后半腔内湍流脉动的抑制,特别是揭示了波形空腔可显著降低临近空腔后壁区域的湍流脉动。
详细分析腔内压力脉动均方根特性可直观地认识空腔内气动噪声环境。见图7,在x3=0截面上3种空腔的湍流压力脉动均方根与图6中各向速度脉动特性具有一定差异,即压力脉动强度在剪切层及空腔后壁面明显占优,表明这些区域的气动噪声强度较高,并且可清晰地观察到剪切层撞击空腔后壁,导致剪切层内湍流脉动贴近后壁面并向下底面转移扩散的动力学特征。矩形方腔内压力脉动强度最大,弧形空腔次之,波形空腔脉动压力强度最弱,它们的共同特点是削弱剪切层内湍流脉动后后壁面及腔底压力脉动随之减弱。进一步地,如图7(b),(d),(f)所示,三维空腔展向压力脉动分布与x3=0截面上基本一致,均体现了剪切层主导空腔内压力脉动分布的特性。细微的差别在于,相对于矩形方腔,弧形空腔压力脉动强度沿展向中心x3=0截面集中,波形空腔压力脉动强度沿展向呈轻微波动分布。

(a) Rectangle cavity:
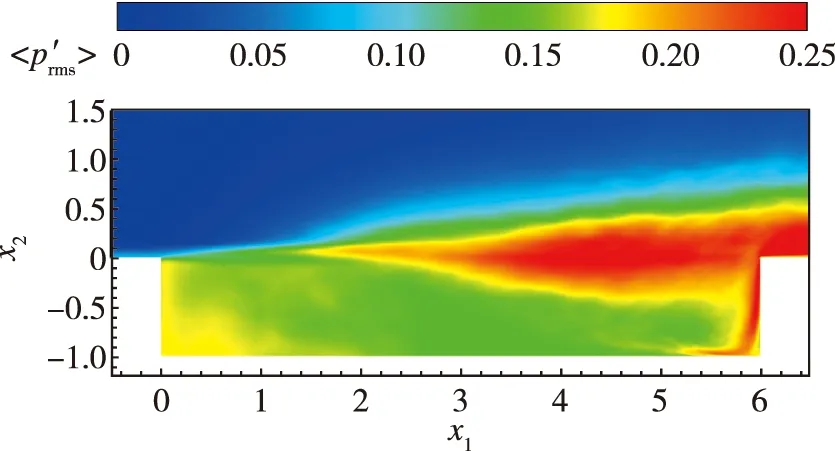
(a) x3=0 cross section of the rectangle cavity


图8 3种空腔腔底壁面中心线OASPLFig.8 OASPL on the bottom wall centerlines of the three cavities
2.2 流动演化特征
基于典型瞬时流场对3种空腔的流动动力学演化特征进行分析,其中采用Q准则显示流场涡结构,利用胀量展示声场并对Q准则等值面着色。图9(a)展示了矩形方腔诱导的超声速瞬态振荡流场及声场。当高速气流流过空腔表面后,自由来流与腔内空气混合形成剪切层,受Kelvin-Helmholtz不稳定性主导,初始剪切层卷起有序的大尺度涡结构,其向下游发展过程中沿展向破碎,构成大量涡团结构。涡团与空腔后壁撞击产生反射压力波,部分压力波经腔内向前传播,另一部分传出腔外受超声速来流Doppler效应辐射向下游远场。图9(b)中,高速气流经过弧形空腔表面后,形成具有一定弧度的剪切层涡结构,其向下游对流失稳特征与矩形方腔的情形相似,大尺度涡结构运动展向空间关联性仍较强,且空腔后壁呈凸面形状,较易向上游反射声波,仍可导致声-流振荡现象。见图9(c),在波形空腔前缘作用下,沿展向形成波状的流向涡结构剪切层,其向下游对流很快沿展向失稳,产生大量小尺度涡。由于展向波状涡破碎快,涡结构展向空间关联性较弱,最终形成较弱的声-流耦合振荡。

(a) Rectangle cavity
图10给出了3种空腔分别在x3=0截面各自几何中心位置随时间的脉动压力及声压级频谱(圆频率)。见图10(a),脉动压力直观地反映出3个空腔均存在周期性振荡信号特征,其中波形空腔压力振荡水平最低,矩形方腔和弧形空腔压力振荡水平接近。观察图10(b)中声压级频谱可以发现,矩形方腔内存在最优频率f3=1.88,次优频率f1=0.84,及另外两个占优频率f2=1.38和f4=2.37。弧形空腔内主导频率与矩形方腔最优频率f3=1.88和次优频率f1=0.84一致且更加清晰。波形空腔内f3=1.88和f4=2.37两个特征频率较为明显,整体频谱幅值较低。根据Rossiter[2]模态公式
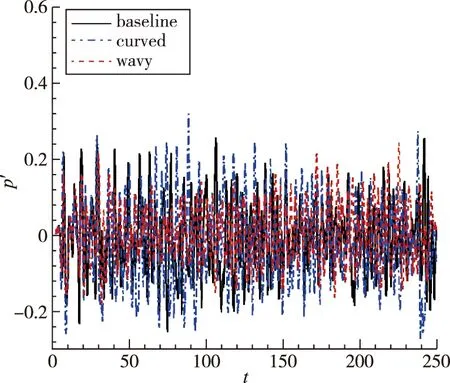
(a) Pressure fluctuation
(8)
其中,fm是第m个模态的频率,u,Ma是自由来流速度和Mach数,取相位移α=0.397,常参数κν=0.66。见图10(b),矩形方腔中第3,4,6,7个Rossiter模态(黑色虚线)特征较为显著,而弧形空腔中第4,7个Rossiter模态消失,波形空腔中则第3,4个Rossiter模态消失,展现出空腔几何构型对Rossiter模态的复杂控制作用。此外,矩形方腔在中心位置上的整体声压级为179.0 dB,波形空腔为177.6 dB,比矩形方腔低了 1.5 dB,弧形空腔为180.0 dB,比矩形方腔高1.0 dB。弧形空腔在该位置声压级较高的现象在图8中已有展示,即其在空腔中心小范围区域内其声压级能够超越矩形方腔。
3 增厚的来流边界层
上述空腔计算中上游均采用均匀自由来流入口边界条件(δ=0,无边界层厚度)。自由来流在空腔前缘表面上发展形成边界层,其到达空腔前缘时厚度较薄。本节在空腔上游入口处设置了发展较充分的厚边界层来流,以探索其经过矩形方腔后对腔内流动及噪声的影响。
具体地,使用常规2阶空间离散精度(Roe格式)的CFD程序计算均匀自由来流条件下Ma=1.4,Re=10 000长平板算例,在平板下游特定流向站位处截取获得流向速度型为厚度δ=0.2边界层条件。将其在方腔上游来流入口处设置为入口边界条件。
图11为增厚的来流边界层入口条件下,LES计算获得的时均流向速度、湍流速度脉动均方根及压力脉动均方根云图。对比图11(a)和图3(a)中的时均流向速度可见,入口边界层增厚后,到达空腔前缘的边界层明显增加,导致剪切层厚度也随之增加。此外,来流边界层增厚后,腔内时均流向速度变化梯度较小,剪切层在后半方腔扩展侵入的区域也较大。将图11(b)与图6(a)中流向速度脉动均方根对比,同样可见剪切层增厚现象,且图11(b)中剪切层及腔内流向速度脉动水平都显著降低。与图6(b),6(c)相比,入口边界层增厚后,见图11(c),11(d),法向和展向速度脉动均方根也均显示在剪切层及腔内流动脉动强度明显降低。图11(e)中压力脉动均方根直观展现了增厚来流边界层可显著降低腔内噪声水平。
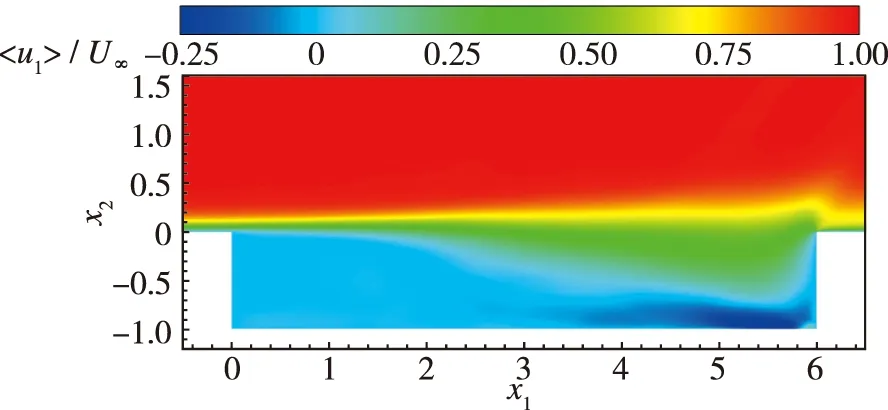
(a) 〈u1〉 / U∞
图12定量对比了均匀自由来流和增厚来流边界层两种入口条件下,空腔底壁面上整体声压级水平。对比表明增厚边界层入口条件下,整体声压级仍呈现为沿流向先降低后升高的分布特征,但其相对于均匀来流的入口条件平均降低底壁面整体声压级约4 dB。对前半腔整体声压级抑制尤其显著,在x1=1.7站位处噪声抑制效果达到最大,即整体声压级降低约4.5 dB。后半腔脉动压力的抑制效果下降,最小时整体声压级仍降低约2.5 dB。
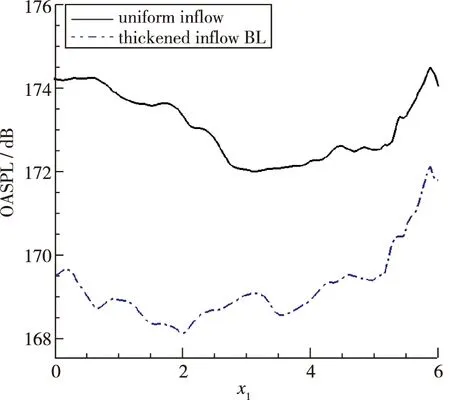
图12 空腔底壁面中心线整体声压级对比Fig.12 Comparison of OASPL on cavity bottom wall centerlines
图13对比了两种入口来流条件下,空腔在x3=0截面内中心位置(x1,x2,x3)=(3,-0.5 ,0)处随时间的压力脉动及声压级频谱。由图13(a)中压力脉动幅值可见,增厚边界层入口条件下空腔内压力振动水平降低,但仍存在周期性脉动特征。具体地,见图13(b),声压级频谱显示原方腔流动第3,4个Rossiter模态被抑制,第6个Rossiter模态(f3=1.77)相应减弱,但第7个Rossiter模态(f4=2.21)增强,表明方腔内声-流振荡现象仍存在。此外,增厚来流边界层的空腔中心位置整体声压级176.8 dB,较均匀自由来流条件约低2.3 dB。
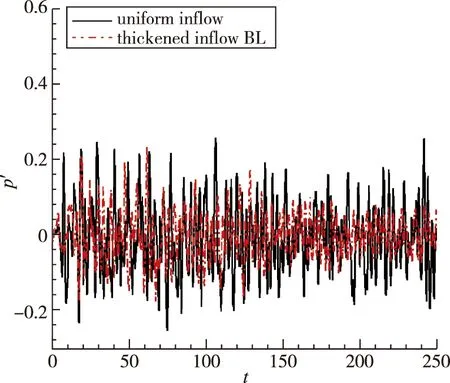
(a) Pressure fluctuation
4 结论
本文利用LES技术计算分析了空腔几何修形和增厚来流边界层条件对超声速空腔流动及噪声的控制效应,得到以下结论:
(1)弧形、波形空腔几何修形,通过调整来流边界层向剪切层转变展向结构,及后续剪切层与空腔后壁的相互作用,控制了剪切层的展向演化及后半腔内湍流结构。相对于矩形方腔,几何修形空腔不仅改变了基本流形态,还整体上降低了腔内湍流速度脉动水平,其中波形空腔比弧形空腔能更有效地抑制腔内的湍流速度脉动。
(2)腔内压力脉动均方根对比直观展示了波形、弧形两种修形空腔相对于矩形方腔的噪声控制效果。空腔底壁面整体声压级对比表明弧形空腔降低了前半腔底壁面噪声1.5 dB,但基本没改变后半腔底壁面噪声。而波形空腔的整体降噪效果更优,特别是相对方腔后壁面整体声压级有显著的下降,最高降幅约2.5 dB。
(3)弧形、波形空腔通过改变剪切层及腔内湍流涡结构,使得流动振荡特征发生了一定的改变。分析声压级频谱,发现弧形、波形空腔均抑制了矩形方腔中部分Rossiter模态,但同时各自也保留了一部分远矩形方腔Rossiter模态,表明弧形和波形空腔中仍存在声-流耦合振荡现象。
(4)增厚矩形方腔上游来流入口边界层厚度,可显著降低方腔内的湍流脉动及气动噪声水平。对比表明,方腔底壁面沿流向整体声压级降低最大时约4.5 dB,最小时约2.5 dB。另外,声压级频谱表明,增厚来流边界层可改变方腔内流动脉动特征频率,即影响了腔内声-流耦合振荡特性。
