变系数Gordoa-Pickering方程的容许变换与对称群*

苏 丹，雍雪林

(1.湛江幼儿师范专科学校数学系，广东 湛江 524084；2.华北电力大学数理学院，北京102206)

非线性发展方程，特别是可积方程，无论从数学角度还是从物理角度都引起了人们极大的研究兴趣[1].近年来，越来越多的学者开始关注变系数非线性偏微分方程，因为这些方程可以提供更真实的模型来描述生活中的一些现象，如变系数非线性薛定谔方程能描述脉冲在非均匀光纤中的传输[2-4],变系数KdV方程能描述非均匀介质中的非线性波动现象[5-7].

值得注意的是，变系数模型都包含以任意常数或任意函数形式出现的变量参数.这些参数也称为模型中的任意元素，它们往往假定取值在一定范围内(任意常数)或者属于某些特定类别的函数(任意函数).这些任意元素的存在使得变系数非线性偏微分方程的求解变得十分困难.基于挪威数学家Sophus Lie提出的对称群理论[8-9]，变系数方程的容许变换被广泛用于方程的等价分类，从而降低原方程的任意性.笔者从微分方程群理论的角度出发，拟研究一个含有6个任意函数的6阶变系数非线性偏微分方程.该方程与包括Kaup-Kupershmidt方程、Sawada-Kotera方程、Boussinesq方程和Hirota-Satsuma方程等在内的许多有趣的可积系统密切相关，研究其对称群结构对理解这些著名方程及其相关的物理背景具有重要意义.

1 变系数Gordoa-Pickering方程

从一个三阶散射问题出发，Gordoa等给出了6阶可积的非线性方程[10]

和

并利用达布变换和贝克隆变换得到了这2个方程的孤立子解[11].笔者将对这2个方程进行推广，给出一个包含6个任意函数的变系数Gordoa-Pickering(Variable Coefficient Gordoa-Pickering，VCGP)方程

(1)

其中a(t),b(t),c(t),d(t),e(t),f(t)为任意非零光滑函数.

考虑如下变换：

(2)

如果变换(2)保持方程(1)的形式不变，即

UXXXXXT+A(T)UXXXTUX+B(T)UXXXXUT+C(T)UXXTUXX+D(T)UXXXUXT+

(3)

但可能改变作为系数的任意函数，那么称变换(2)为VCGP方程的容许变换.笔者将采用直接法寻找变换(2)的具体形式.

2 容许变换

根据文献[6]，可以选择更简单的形式代替变换(2)，即假设

(4)

且满足Tt(XxUu-XuUx)≠0，由此可以得到函数u=u(x,t)与U=U(X,T)各阶导数之间的变换关系.例如，

(5)

其中Dt=∂t+ut∂u+uxt∂ux+utt∂ut+…和Dx=∂x+ux∂u+uxx∂ux+utx∂ut+…是关于变量t和x的全导数算子.

将方程组(4)，(5)代入方程(3)，并利用方程(1)进行化简，经过一系列分析和计算可得如下结论：

定理1方程(1)的容许变换为

X=c1x+c2,T=T(t),U=c3u+c4.

其中：ci(i=1,2,3,4)为任意常数，满足c1c3≠0；T(t)为任意光滑函数，满足Tt≠0，且方程(1)和(3)中的任意系数变换关系为

3 李点对称群与相似约化

由定理1可知方程(1)的容许变换均为局部保纤变换，于是可以从容许变换直接得到该方程保持解不变的李点对称群.

定理2对于任意系数a(t),b(t),c(t),d(t),e(t),f(t)，方程(1)的李点对称变换为

对应的群无穷小生成元为

V1=∂x,V2=∂u,V3=u∂u-x∂x.

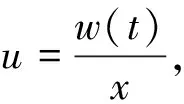
(e+2f)w2-(6a+24b+4c+6d)w+120=0.

上述李点对称群适用于含有任意系数且保持系数不变的方程.特别地，当任意系数均为常数时，有以下结论：

定理3当方程(1)中的任意系数均为常数时，该方程的李点对称变换为

对应的群无穷小生成元为

V1=∂x,V2=∂u,V3=u∂u-x∂x,Vα=α(t)∂t，

其中T(t),α(t)为任意非零光滑函数.

此时，对应生成元V1+V2+Vα的相似约化为

u=F(t)+w(z),z=x-F(t),

(6)

再假设φ(z)满足椭圆方程

(7)

将(7)式代入(6)式后得到一个关于φ(z)的多项式，提取φ(z)各次方的系数进行求解，可得如下4种情况：

根据以上4种情况，由方程(7)的解φ(z)可以构造出方程(1)的精确解.这里以第4种情况为例加以说明.不妨假设b=4m2(m≥0),k3=1，此时，方程(7)有解

φ(z)=-4m2sech2(mz).

于是，当方程(1)中任意系数满足

a(t)=a,b(t)=4m2,c(t)=-d-9,d(t)=d,e(t)=-(4m2+3)(4m2+3+a),

f(t)=4m2(4m2+3+a)

时，方程(1)存在扭结型孤子解

u(x,t)=F(t)-4mtanh(m(x-F(t))).

(11a+35b+11c+17d)wzwzz-(2e+f)wwzwzz=0.

这是一个6阶常微分方程，笔者将在以后的工作中对其进行深入研究.

4 结语

利用直接方法找到了一个包含6个任意函数的6阶变系数偏微分方程的容许变换，该变换保持方程形式不变但可能改变方程中的任意系数.在此基础上，给出了保持方程系数不变的李点对称变换及相应的相似约化，并构造出特殊的群不变解.利用定理2和定理3，可进一步研究包含6个任意函数的6阶变系数偏微分方程的对称约化、精确解和守恒律等.