拉伸加载下PBX 炸药力学性能的分子动力学模拟

高飞艳，刘 睿，陈鹏万，龙 瑶，陈 军,3

（1. 北京理工大学爆炸科学与技术国家重点实验室, 北京 100081；2. 北京应用物理与计算数学研究所, 北京 100088；3. 北京大学应用物理与技术中心, 北京 100871）

聚合物黏结炸药（polymer bonded explosive，PBX）是一种高度填充的颗粒复合材料，主要由含能单质炸药晶粒和聚合物黏结剂以及其他增塑剂、钝感剂等混合而成[1-3]。PBX 具有低感度、高爆速、良好的物理安定性等特点，广泛应用于火箭推进剂、弹头和采矿等军事和民用领域。相对于单质炸药晶粒，黏结剂的弹性模量相对较低且易于变形，在低速撞击、拉伸和压缩等外部刺激下，复杂的热-力-化学耦合反应可能沿着炸药晶体与黏结剂之间的界面产生，从而影响PBX 的稳定性[4-5]。因此，研究炸药晶体与黏结剂之间的界面行为对于PBX 的设计和应用具有重要意义。

目前，人们对PBX 的力学行为、结构变形和断裂机理开展了大量研究。例如：Yeager 等[6]通过中子反射仪观察到在HMX 晶体与黏结剂Estane 之间存在一个明显的界面混合层（厚度约6 nm），该混合层可能影响黏结剂与炸药之间的界面附着力；Rae 等[7]通过巴西实验研究了PBX 的拉伸断裂行为，发现微裂纹通常在大颗粒的边界形成，并垂直于加载方向扩展，导致PBX 断裂，在裂纹处黏结剂被拉成纤维细丝，这被认为会影响炸药的拉伸强度；Xiao 等[8]通过动态拉伸实验研究了RDX 基PBX 的拉伸性能，发现其拉伸行为表现出明显的高应变率依赖性，炸药颗粒与黏结剂之间的界面脱粘是主要的失效模式。然而，仅通过实验很难完全揭示PBX 在拉伸加载下的力学响应，如应力局部化、微观结构演变等。

数值模拟方法是研究PBX 力学行为的有效手段，近年来，人们针对含能晶体、聚合物黏结剂及损伤界面提出了不同的本构模型。Wang 等[9]考虑了由于黏结剂破裂和脱粘引起的速率相关损伤，为黏结剂与PBX 界面建立了损伤黏弹性模型，并模拟了PBX9501 的动态力学响应，发现PBX9501 的拉伸强度与应变速率有关，且断裂方式为黏结剂脱粘。Dai 等[10]使用内聚力模型（cohesive zone modeling，CZM）研究了PBX9501 在单轴准静态拉伸下的失效演化，发现在整个拉伸过程中，拉伸应变起源于较软的黏结剂，拉伸应变的持续累积导致黏结剂脱粘。分子动力学（molecular dynamics，MD）方法作为一种广泛使用的数值模拟技术，可以揭示界面局部结构演化和微观力学行为[11-14]。Xiao 等[15-17]应用COMPASS 力场计算了一系列HMX 基PBX 炸药的弹性力学性能，提出了多种黏结剂（Estane5703、PEG、PVDF、PCTFE 等）对PBX 结构和力学性能的影响。Wang 等[18]通过MD 模拟研究了应变率对RDX 基PBX 的动态力学响应和失效机制的影响，发现PBX 的初始损伤主要发生在黏结剂区域。Lv 等[19]使用MD 模拟研究了温度和应变率对TATB-F2314 界面力学性能及微观结构的影响，发现黏结剂F2314 会扩散进入TATB 层，导致TATB-F2314 界面处出现“内嵌状”界面混合层，并且随着温度的升高，界面混合层厚度逐渐增大。目前，通过MD 方法，在原子尺度上对含能晶体-黏结剂界面的微观变形机理和力学性能的研究较少，主要原因是难以建立高颗粒填充且能真实反映PBX 细观特性的结构模型。

本研究通过MATLAB 编程建立复杂的PBX 炸药模型，即含氟聚合物F2311 包覆在多个以HMX为基的炸药颗粒外形成HMX-F2311 界面模型，采用MD 方法模拟单轴拉伸下HMX-F2311 炸药的力学性能，通过分析HMX-F2311 的拉伸应力-应变曲线、界面微观结构演变和能量分布，探讨应变率对PBX 力学性能的影响。

1 力场和模型的建立

1.1 力 场

HMX-F2311 的力场由HMX 势、F2311 势以及HMX 与F2311 之间的界面相互作用势组成，因此HMX-F2311 系统的总能量可写为

1.2 初始模型

首先，使用MATLAB 程序建立F2311 包覆HMX 的PBX 界面初始模型，如图1(a)所示。模型中x、y方向各有4 个HMX 晶体颗粒，z方向有2 个HMX 晶体颗粒，黏结剂F2311 均匀包裹在颗粒的边缘。模型尺寸约为200 Å×200 Å×100 Å，原子数约为280 000。

HMX-F2311 界面模型的优化过程分为4 个步骤：能量最小化、优化原子坐标、退火消除残余应力以及获得平衡构象。首先，对HMX-F2311 界面模型进行几何弛豫，采用力收敛公差为10-8kcal/(mol·Å)的共轭梯度法进行能量最小化。其次，在NPT系综下进行MD 模拟，以优化原子坐标，压力为标准大气压，温度为300 K，步长为0.1 fs，模拟时间为40 ps。接着，为降低系统的能量，消除残余应力，对模型进行退火处理。将体系温度迅速上升至350 K，弛豫50 ps 后，降至300 K，继续弛豫50 ps。退火过程在NPT系综下进行，模型尺寸将发生明显变化。最后，采用NVT系综对体系进行结构优化，模拟时间为20 ps。优化后的HMX-F2311 界面结构见图1(b)。NVT优化过程中的压力和能量随时间的变化曲线如图2 所示。系统的压力和能量最终趋于稳定，上下波动小于5%，表明此时HMX-F2311 结构达到平衡。将模拟得到的平衡结构作为初始构型，进行不同应变率下单轴拉伸的MD 模拟。

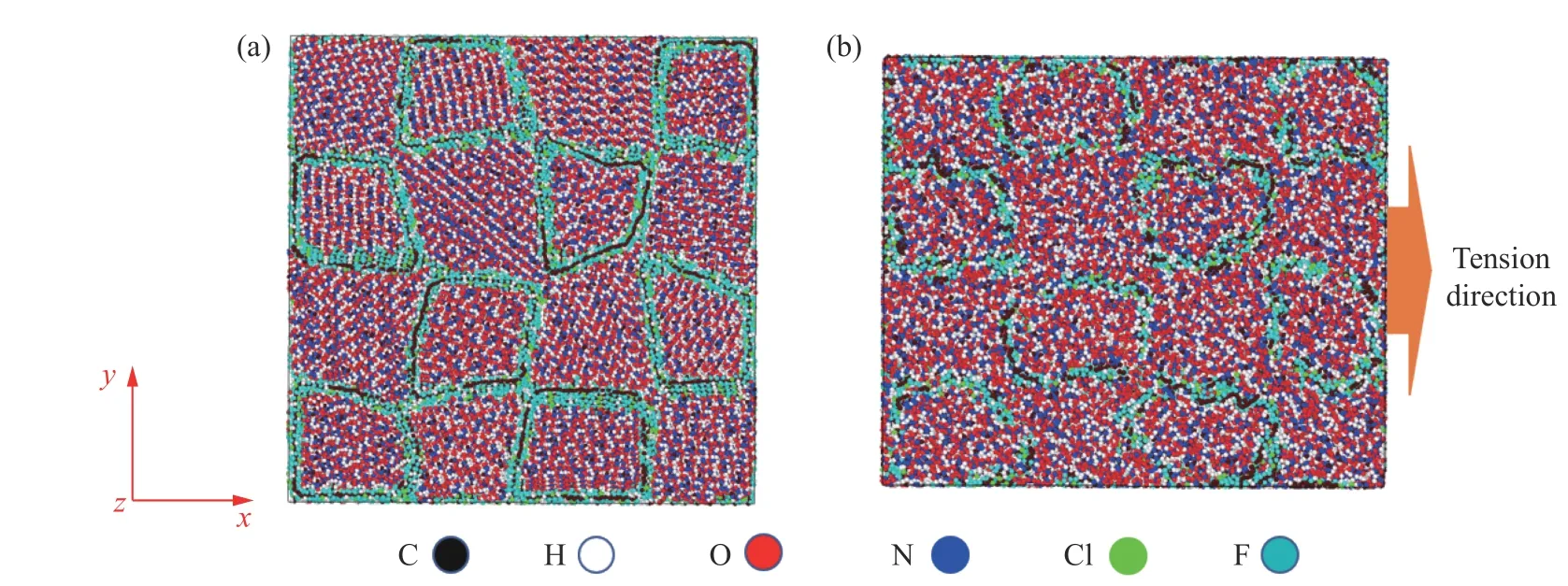
图1 HMX-F2311 界面的初始模型(a)以及优化后HMX-F2311 界面的稳定结构(b)Fig. 1 Initial model of HMX-F2311 interface (a) and the stable structure of HMX-F2311 interface after optimization (b)

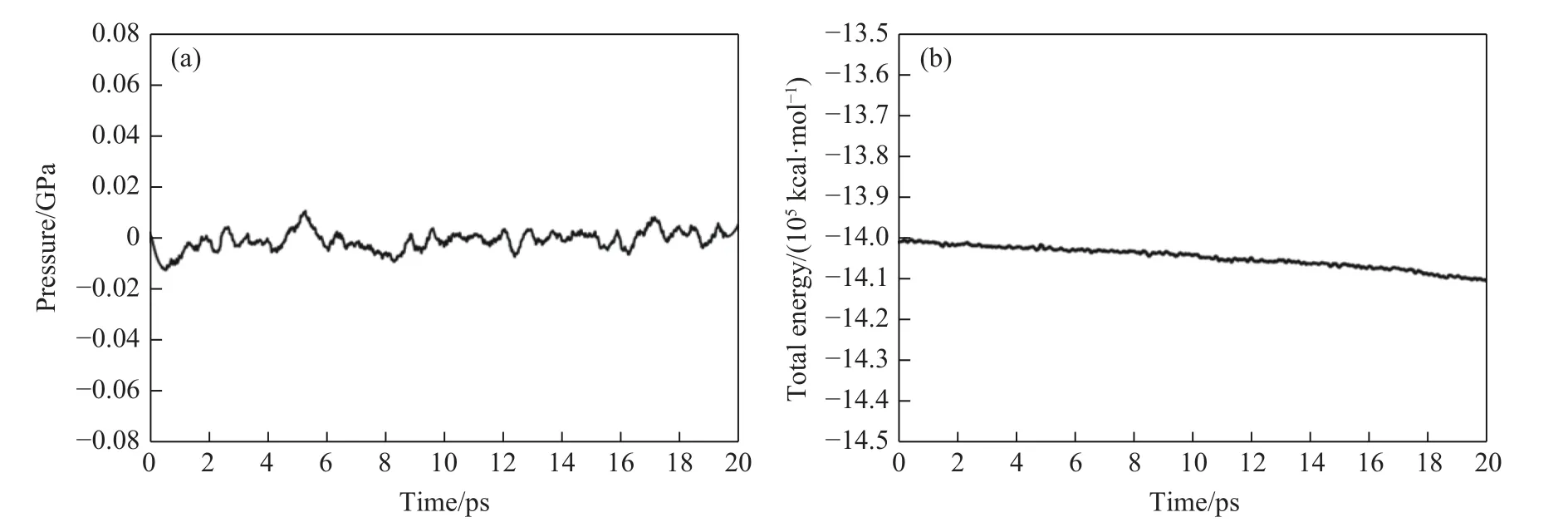
图2 优化过程中压力和能量随时间的变化Fig. 2 Pressure and energy fluctuations vs. time during optimization

1.3 拉伸加载

2 动态拉伸下应变率对PBX 界面的影响

为了研究应变率对HMX-F2311 界面拉伸变形的影响，在应变率为0.5×1010、1.0×1010、2.5×1010和5.0×1010s-1下进行了一系列动态拉伸模拟，应力-应变曲线如图3(a)所示。不同应变率下的拉伸应力-应变曲线表现出相似的特征，均可分为3 个阶段：弹性阶段（Ⅰ）、塑性阶段（Ⅱ）和破坏阶段（Ⅲ）。在拉伸加载初期，应力随应变的增加而线性增加，即弹性阶段（ ε=0.025）；在应力-应变曲线中没有明显的屈服点，应力持续非线性增加至PBX 的拉伸强度（ ε=0.080），即塑性阶段；达到拉伸强度后，随着应变的增大，应力持续减小，PBX 的力学性能逐步劣化失效，为破坏阶段。在模拟中，采用应力-应变曲线中的极值应力作为PBX 的拉伸强度，并将弹性阶段的应力-应变曲线斜率作为PBX 的弹性模量。如图3(b)和图3(c)所示，拉伸强度和弹性模量均随拉伸应变率的增加而增大，随对数应变率的增加而线性增大。

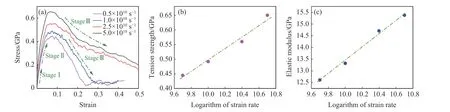
图3 HMX-F2311 在不同应变率下的应力-应变曲线 (a)以及拉伸强度 (b) 和弹性模量 (c) 与对数应变率的关系Fig. 3 (a) Stress-strain curves of HMX-F2311 under different tension loading; (b) tension strength vs.logarithmic strain rate; (c) elastic modulus vs. logarithmic strain rate

为了比较不同应变率（0.5×1010、1.0×1010、2.5×1010和5.0×1010s-1）下PBX 的微观结构演变，通过OVITO 可视化程序计算了拉伸过程中每个原子的局部应变分布，如图4 所示。在低应变率（0.5×1010、1.0×1010s-1）拉伸加载下：当 ε =0.05 时，靠近黏结剂区域的应变明显高于炸药晶体的内部应变，表明在拉伸加载下原子应变主要集中在较软的黏结剂F2311 上；当应力达到拉伸强度后（ ε=0.10），炸药晶体与黏结剂F2311 界面处出现了部分孔洞和微裂纹；当 ε =0.15 时，靠近加载侧的界面逐渐开裂，出现黏结剂脱粘现象；随着拉伸的持续，黏结剂的脱粘降低了PBX 的承载能力，导致材料的力学性能逐渐劣化；当 ε=0.25时，PBX 的拉应力降到最低，在靠近加载侧的界面处沿垂直于加载方向产生了一条主裂纹。PBX 的失效模式为黏结剂脱粘。

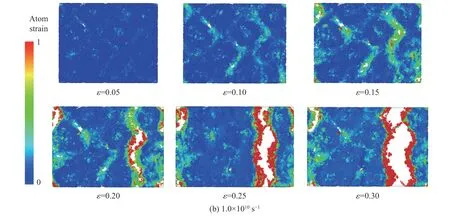
图4 不同拉伸加载应变率下HMX-F2311 界面在x 方向的应变分布Fig. 4 Distribution of strain field in the x direction of HMX-F2311 interface under different tension strain rates

如图5 所示，相比于低应变率拉伸加载，在高应变率（2.5×1010和5.0×1010s-1）拉伸加载下，PBX 微观结构演变整体上差异不大。加载初期，PBX 的拉伸原子形变主要集中在软黏结剂附近。随着拉伸的持续，相对较弱的HMX-F2311 界面发生脱粘。不同的是，在低应变率拉伸下形成了一条大致垂直于加载方向的主裂纹，且断裂位置靠近加载面一侧。随着拉伸应变率的增加，在远离加载侧的界面处也出现了大量微裂纹，破坏路径分布在整个模型上。当 ε =0.20 时，低应变率拉伸加载下HMX-F2311 靠近加载侧的界面处已经产生了一条裂纹，而高应变率加载下HMX-F2311 界面处只存在孔洞，裂纹并未开始扩展，表明随着应变率的增大，HMX-F2311 的抗拉性能增强。HMX-F2311 在单轴动态拉伸下的断裂失效是由于黏结剂脱粘，与Rae 等[7]通过显微镜观察到的断裂方式相似。

图5 不同拉伸应变率下HMX-F2311 界面在x 方向的应变分布Fig. 5 Distribution of strain field in the x direction of HMX-F2311 interface under different tension strain rates

为了从能量角度理解PBX 在单轴拉伸过程中的形变机制，分析了不同拉伸应变率（0.5×1010和5.0×1010s-1）下PBX 界面的势能随应变的变化情况，如图6 所示。在低应变率（0.5×1010s-1）拉伸加载下：当PBX 拉伸处于弹性阶段和塑性阶段时，势能随着应变的增大逐渐增大；当达到HMX-F2311 的拉伸强度时，势能也达到极值（0.68×104kcal/mol），随后迅速下降。然而，在高应变率（5.0×1010s-1）拉伸加载下，当达到HMX-F2311 的拉伸强度后，势能仍然持续升高至极值（3.26×104kcal/mol），随后下降。随着拉伸应变率的增加，HMX-F2311 的势能增加了4 倍。

图6 不同应变率下总势能随应变的变化Fig. 6 Variations of potential energy with stain under different strain rates

模拟体系的势能一般分为成键相互作用和非键相互作用，其中：成键相互作用主要包括键能、角能、二面角能以及非正常二面角扭转能等，而非键相互作用包括范德华力作用和库仑相互作用。拉伸应变率为0.5×1010和5.0×1010s-1时PBX 界面各势能分项随应变的变化曲线如图7 所示。为了便于分析，势能以及各能量分项均减去未拉伸时的初始值，其中：ΔEpotential、ΔEbond、ΔEangle、ΔEdihed、ΔEvdwl、ΔEimp分别为势能、键能、角能、二面角能、范德华力相互作用能、非正常二面角扭转能的变化量，ΔEvdwl、ΔEbond、ΔEangle、ΔEdihed以及ΔEimp均由LAMMPS 直接输出。从图7 可以看出：单轴拉伸过程中影响势能变化的主要因素是范德华力相互作用，尤其在5×1010s-1的高应变率下，范德华力相互作用对势能的变化起决定性作用；成键能对势能的贡献较小，其值随应变率的变化不明显；键能和角能在拉伸过程中对势能有一定的影响，尤其是弹性和塑性阶段；二面角能和非正常二面角扭转能在整个拉伸过程中几乎没有变化。

图7 不同应变率下各个势能分项随应变的变化Fig. 7 Variations of each energy sub-item of potential energy with strain under different strain rates

PBX 的势能随拉伸应变率的增加而快速增大的原因可能与黏结剂F2311 的构象有关。在较低的拉伸应变率下，F2311 链有更多的时间进行平衡，并在每一步拉伸后进行滑动、旋转和展开以达到平衡，从而减少界面变形的约束。然而，在高应变率下，F2311 链改变原子取向的时间较短，导致HMXF2311 界面处的非平衡状态和更大的变形阻力，从而需要较大的应力才能使PBX 界面进一步形变。由此可知，低应变率更有利于黏结剂F2311 达到构象平衡。

3 结 论

采用MD 方法模拟了HMX-F2311 在不同拉伸速率下的力学性能和断裂机理，得到如下结论。

(1) HMX-F2311 的力学性能表现出高应变率依赖性。拉伸强度和弹性模量随着应变率的增加而增大，并与对数应变率呈线性关系。

(2) 在单轴拉伸加载下，应变主要集中在黏结剂F2311 附近，并逐渐在界面处形成孔洞和裂纹。PBX 的断裂是由于黏结剂F2311 的脱粘。在低应变率下形成了一条垂直于加载方向的主裂纹，随着拉伸应变率的增加，破坏路径将分布在整个模型上。

(3) 在单轴拉伸加载过程中，HMX-F2311 的势能随拉伸应变率的增加而迅速增大。在高应变率下，范德华力相互作用对拉伸过程中势能的演变起决定作用。

研究结果对于理解PBX 界面的微观结构演变及失效机理具有重要意义，也有助于通过建立材料微观结构与性能之间的关系设计和改进PBX 复合材料。