页岩油资源规模分布模型及敏感性研究

2022-08-10卢振东刘成林曾晓祥臧起彪吴育平李国雄冯德浩

石油实验地质 2022年4期

卢振东，刘成林，曾晓祥，阳宏，臧起彪，吴育平，李国雄，冯德浩

1.油气资源与探测国家重点实验室，北京 102249；2.中国石油大学(北京) 地球科学学院，北京 102249

近年来，随着国内外对致密油气、页岩油气等非常规油气的重视程度不断加大，推动了全球非常规油气勘探开发快速发展，非常规油气资源评价也得到快速发展[1-6]。国外最常用的资源评价方法包括类比法、单井储量估算法、体积法、发现过程法和资源空间分布预测法等[7]。非常规油气资源评价方法可归纳为类比法、统计法和成因法三大类[8]。郭秋麟等[9]指出，我国所处勘探开发阶段，页岩油资源评价可优先采用三种便捷评价方法，即分级资源丰度类比法、单井估算最终可采量(EUR)类比法和小面元容积法。在不断对非常规油气资源评价方法的探索过程中，如何将早已研究成熟的、熟悉的常规油气资源评价方法运用到非常规油气中去，是资源评价方法的一个重要方向。常规油气资源评价中的一个重要方面是预测油气田数目及其规模分布。APRS和ROBERTS在1958年发表了第一张油气藏规模分布图[10]，其后60多年，提出了多种油气藏规模分布模型和方法并应用于评价中。从油气藏规模分布模型的产生[11-12]，经过自然总体油气藏规模是对数正态分布还是反“J”形分布的讨论[13-14]，不同油气藏规模分布模型的对比[15]，发展到今天对油气藏规模分布的敏感性研究分析[16]。油藏规模分布法的适用条件是中高勘探程度的常规油气藏，如何使油藏规模分布法适用于非常规油气资源评价中，进行油气藏规模分布的敏感性研究，是本文的研究重点。

1 区域地质背景

研究区为合水地区X230井区，面积约为151 km2，位于鄂尔多斯盆地西南部，构造位置为伊陕斜坡(图1)。研究的目的层位是上三叠统延长组长7段，属于半深湖—深湖环境，发育多种类型的重力流沉积[17-19]；岩石类型主要为长石质石英砂岩，黏土矿物以伊利石和绿泥石为主。该区紧邻中生界延长组生烃中心，油气来源充足[20-21]。储层整体十分致密，孔隙度为8.5%～10.5%，渗透率为(0.08～0.17)×10-3μm2，属于超低孔—超低渗储层。X230井区的地质资源丰度约为45×104t/km2，地质资源量约为0.68×108t。

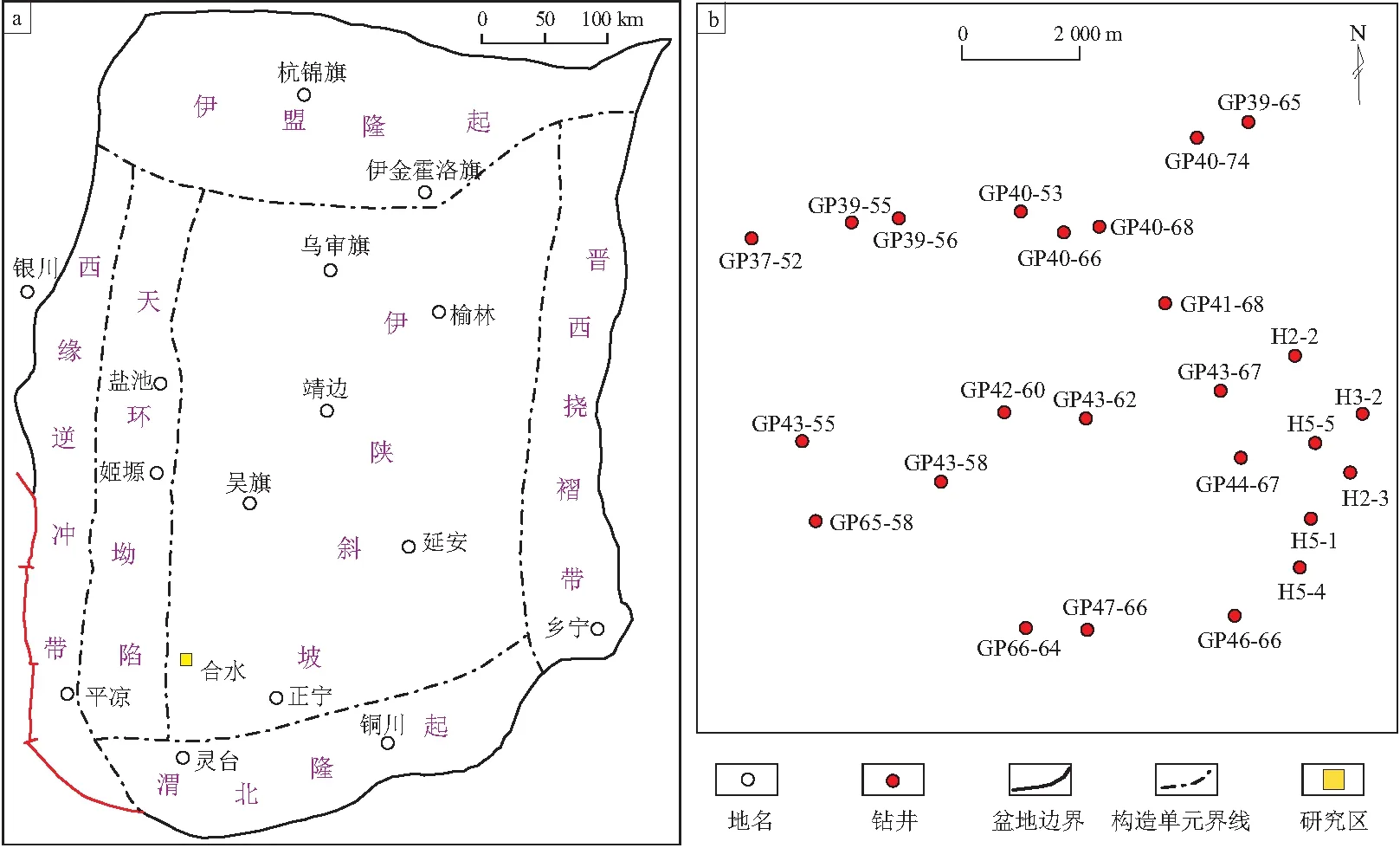
图1 研究区位置(a)及部分井位分布(b)

2 建立油藏规模分布模型

2.1 确定评价单元

油藏规模分布反映的是一个盆地中自然存在的油气藏分布特征、油气发现过程的效率和经济条件对多数小油气藏开发的限制[13]。统计表明，一个评价单元内油藏规模分布遵循一定的统计规律；在发现过程模型法中，是用对数正态分布描述一个区带中油藏的规模分布。

在常规油气资源评价中，油藏规模分布法的基本原理是：在一定的研究区域中，分布一定油气藏的数量，所有油气藏对应的资源量看作一个集合，服从一定的分布规律，常见的有对数正态(Lognormal)分布或者帕累托(Pareto)分布，我们一般称之为“母体”。已发现的油气藏类似于不放回的随机取样，在一定程度上也反映母体的分布特征，通过已发现油藏的规模分布特征反演出母体的油藏规模分布。而在非常规资源中，油气是连续分布的，没有明显的油气水边界，按照一个油藏为一个单位的思想则无法使用。解决办法是：以井为单位，一口井的单井最终可采储量(EUR)作为评价单元的油气储量，这组数据便是在研究区内已发现的油藏规模分布。关于EUR的求取方法比较多，如递减法、双曲线递减法、经验公式法等，本文采用的是双曲线递减法。

2.2 油藏规模分布模型的建立

目前对存在的自然总体分布模型(母体)有两种观点：一是认为对数正态分布是代表油气藏规模母体的一个好的模型，在勘探程度较高的含油气盆地中，已发现的不同规模的油气藏用对数正态分布拟合结果非常理想；二是认为油藏规模分布服从反“J”形态分布，如帕累托分布。康托罗维奇院士在研究世界油气藏资料后认为，这种分布服从帕累托分布[15]。20世纪80年代以后，考虑到经济、技术及其他因素综合作用的影响，SCHUENEMEYER和DREW根据不同时期已发现油气藏分布形态变化规律，推测油气藏规模母体的分布形式应该为对数几何分布(帕累托分布的离散形式)[12-13]。

ATTANASI和CHARPENTIER对比分析了对数正态分布和帕累托分布[15]，认为在模拟参数完全相同的条件下，对数正态分布模拟的结果比帕累托分布的要小15%左右。原因是在对数正态分布模拟中，大油气藏和小油气藏的个数都比帕累托分布的少；对数正态分布反映的只是帕累托分布中的一部分，而不能很好地反映自然总体分布模型的全貌[22]。因此，本文采取帕累托分布模型进行模拟分析。

2.2.1 帕累托分布模型

在前文中确定好评价单元后，可以得到81口井的EUR数据(表1)，以此为基础，建立自然总体分布的油藏规模分布模型。

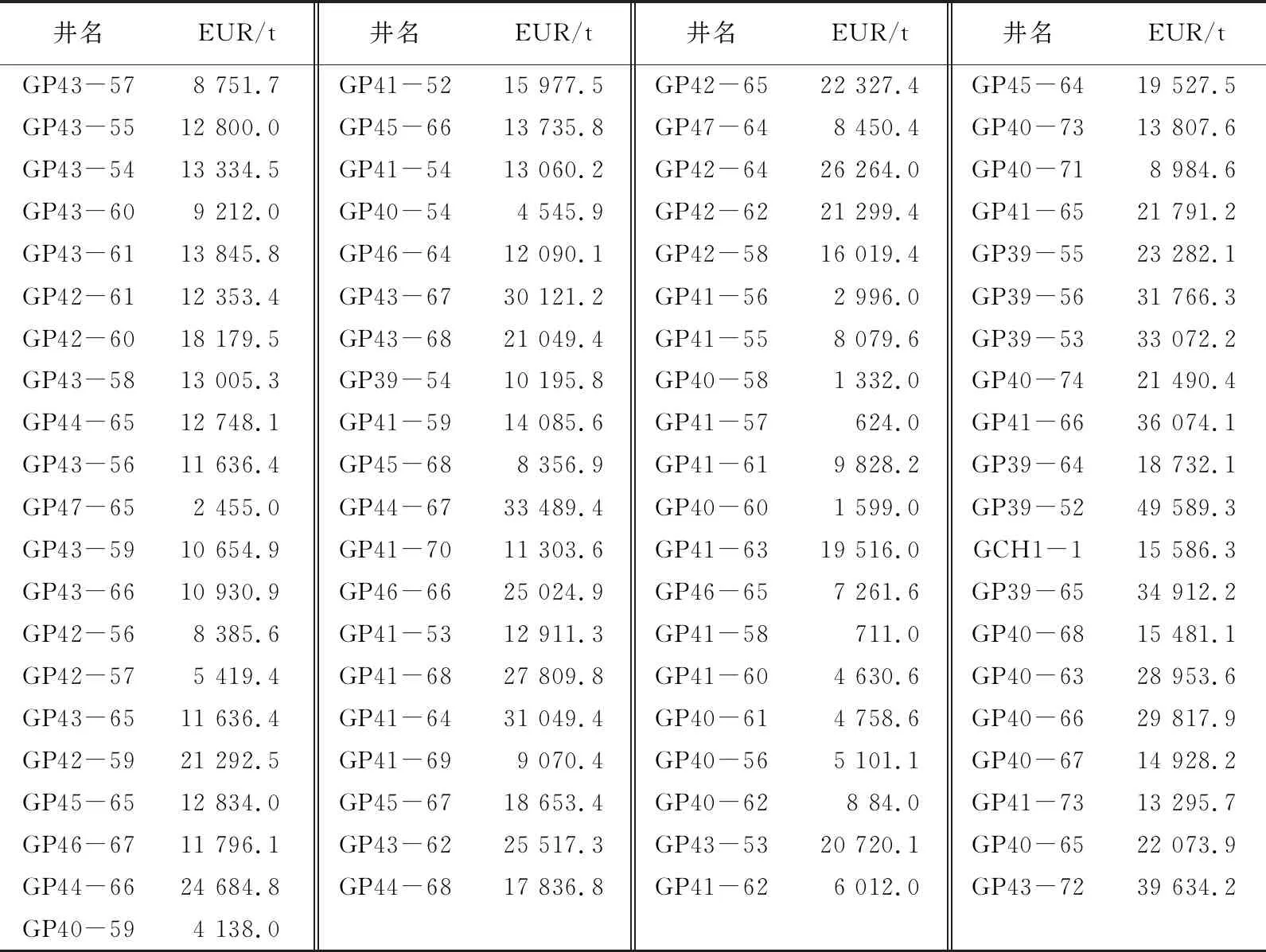
表1 鄂尔多斯盆地合水地区X230井区单井EUR统计

(1)以EUR数据为基础，使用概率统计方法拟合出研究区油藏分布模型的类型，并获得相关的特征参数(位置参数、形状参数)。

现有数据拟合显示，已发现的油藏规模呈现对数正态分布(图2)。而前人研究认为，帕累托分布比对数正态分布能更好地表示油藏规模分布的全貌，所以采用帕累托模型作为母体分布。研究区帕累托分布的形状参数β=0.33，位置参数L=601.34(图3)。

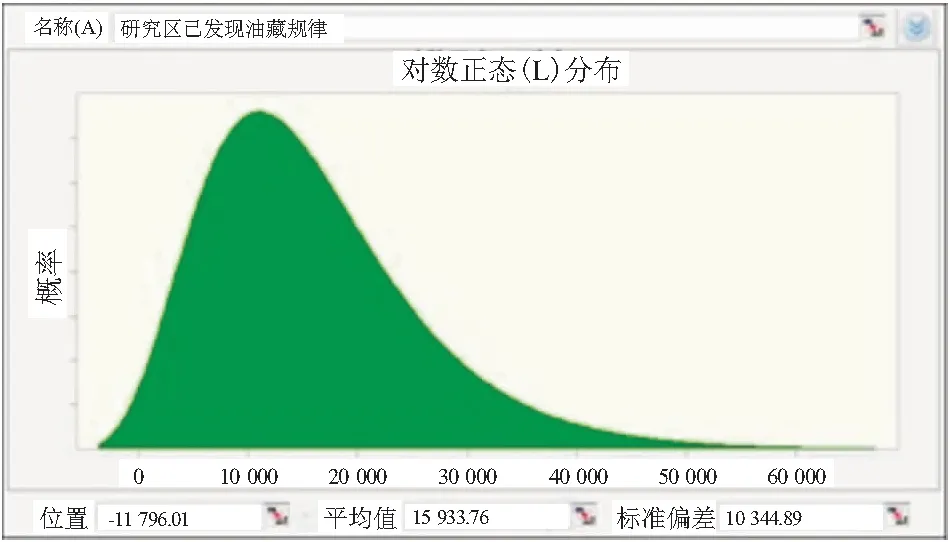
图2 概率统计方法拟合对数正态油藏规模分布模型

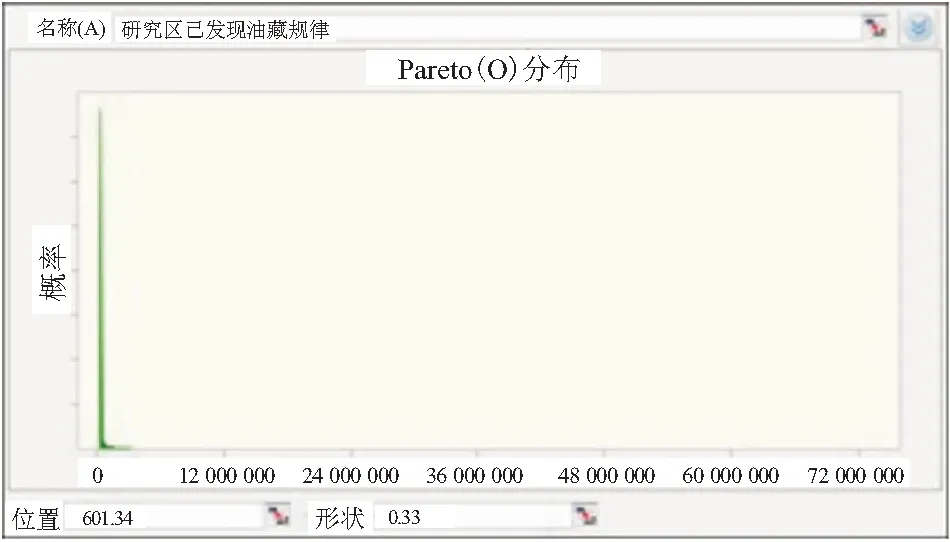
图3 概率统计方法拟合帕累托油藏规模分布模型

(2)在特征参数得到后，使用蒙特卡洛迭代法，模拟生成一组10 000个值的数据(母体)。

(3)从模拟出的数据中，随机导出4组数据体(对应的形状参数β分别是0.41，0.49，0.51，0.52)，每组数据4 000个。

(4)建立以帕累托分布为自然总体分布的油藏规模分布模型，并编写一套程序，研究在不同的形状参数下，分别以25，50，100，200，300，400，500，600，800，1 000为间隔随机抽取数据，每个间隔20组，用以分布模型形状参数β的模拟；并分析油藏发现个数(N)的增加和勘探系数(E)的提高对油藏规模分布模型和参数变化的影响，以及探讨分布模型的敏感性。随机抽样的原则缘于卡夫曼的思想，即油藏发现的过程等同不放回的取样，油藏只能被发现一次，大油藏优先被发现[11]。

2.2.2 自然总体分布验证

为了验证所选自然总体分布模型的准确性，根据随机取样原理对其进行抽样处理。从一组数据体中抽出300个样本量并对其进行分布类型模拟，结果发现，在20次模拟中，19次是对数正态分布，1次是伽马分布(图4)。说明以帕累托为油藏规模分布模型的自然总体是可行的。

图4 自然总体随机抽样分布类型柱状图

3 分布模型的敏感性研究

敏感性研究是油藏规模分布模型研究的重点和热点，准确而客观地认识规模分布模型的特征和影响因素是研究的重要组成部分[23]。此次敏感性分析根据随机取样和偏态抽样原理建立起一套完整的程序，对油藏规模的自然总体进行抽样模拟，用以研究影响油藏规模分布模型的敏感性因素及影响范围。影响帕累托分布的两大参数分别是位置参数(L)和形状参数(β)。位置参数取决于最小的油藏规模值，因此研究油藏规模分布的敏感性，就是研究形状参数的敏感性。下面研究分布模型对自然总体分布油藏个数(N)、自然总体分布模型的形状参数(β)和勘探系数(E)的影响。

3.1 分布模型对自然总体分布油藏个数(N)的敏感性

3.1.1 形状参数(β)为0.41

当β=0.41时，由自然总体分布油藏个数(N)与形状参数(β)的交汇图(图5)发现，随着发现油藏个数的增加，油藏分布模型的形状参数逐渐减小。当油藏个数为25时，模拟的20组形状参数的离散程度很大(β=0.48～1.56)，形状参数中值(F50)为0.85；当油藏个数为50个时，20组形状参数的离散程度减小(β=0.63～1.03)，形状参数中值为0.67。随着油藏不断发现，形状参数的离散程度明显减小，形状参数中值也逐渐降低至0.55～0.60附近。

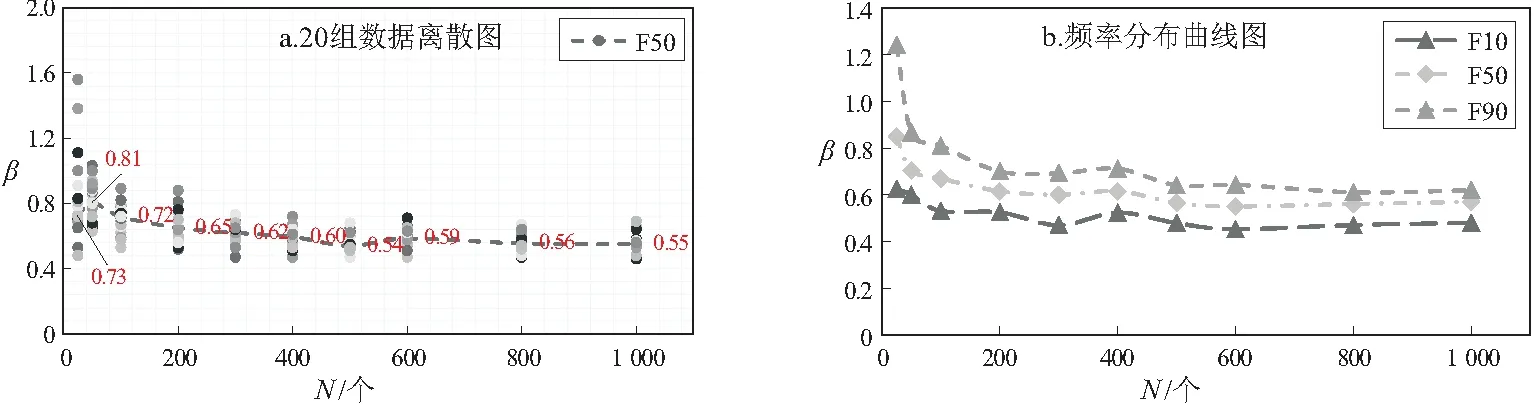
图5 油藏发现个数(N)与油藏规模分布形状参数(β=0.41)交会图

出现这样的情况可能是形状参数的稳定、油藏已发现个数增多的结果。卡夫曼认为，大油藏被发现的概率是最大的，一般在勘探前期发现；较小的油藏被发现的概率较小，一般在中后期被发现。发现个数较少时，大油藏和小油藏构成的分布总体差异比较大，每一个大油藏的发现都会影响形状参数的变化，所以导致20组形状参数离散程度大。而在后期，大油藏基本上都被发现，分布总体的整个形态已经确定，这时整体的形状参数比较稳定，离散程度低，形状参数也比较低。

3.1.2 形状参数(β)为0.49

当β=0.49时，由图6可发现，随着发现油藏个数的增加，油藏分布模型的形状参数逐渐减小。当油藏个数为25时，模拟的20组形状参数的离散程度很大(β=0.57～1.37)，形状参数中值为0.86；当油藏个数为50个时，20组形状参数的离散程度减小(β=0.48～1.00)，形状参数中值为0.77。随着油藏不断发现，形状参数的离散程度明显减小，形状参数中值也逐渐降低至0.52～0.60附近。整体形态与β=0.41的曲线相似，不同之处在于β=0.49的频率分布曲线图中，N=100时，形状参数中值从0.77升至0.79，然后降低至0.64。

图6 油藏发现个数(N)与油藏规模分布形状参数(β=0.49)交会图

3.1.3 形状参数(β)为0.51

当β=0.51时，由图7可发现，随着发现油藏个数的增加，油藏分布模型的形状参数逐渐减小。当油藏个数为25时，模拟的20组形状参数的离散程度很大(β=0.48～1.56)，形状参数中值为0.73；当油藏个数为50个时，20组形状参数的离散程度减小(β=0.63～1.03)，形状参数中值为0.81。随着油藏不断发现，形状参数的离散程度明显减小，形状参数中值也逐渐降低至0.56～0.59附近。

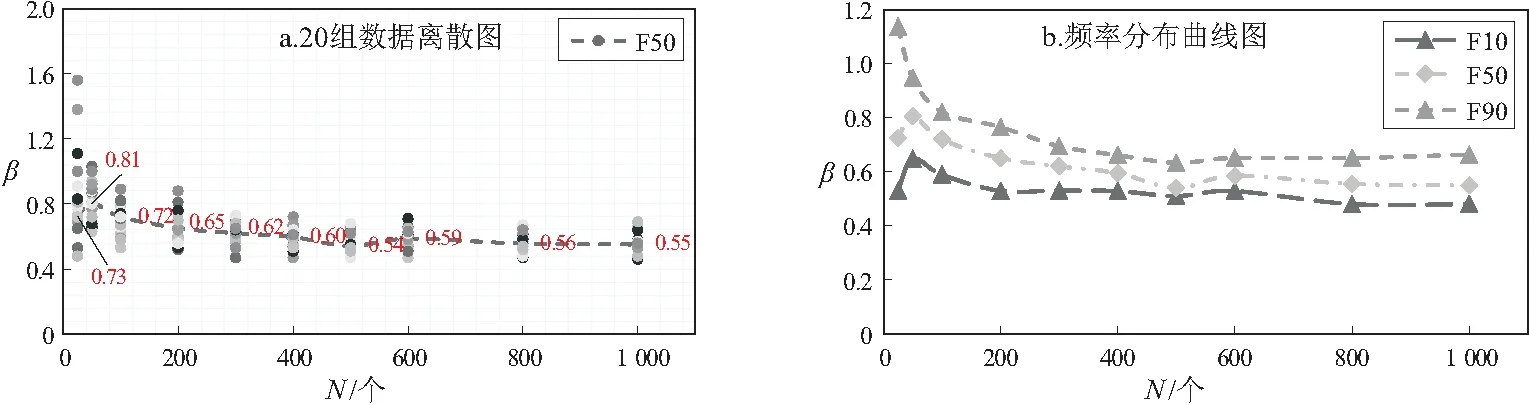
图7 油藏发现个数(N)与油藏规模分布形状参数(β=0.51)交会图

3.1.4 形状参数(β)为0.52

当β=0.52时，由图8发现，随着发现油藏个数的增加，油藏分布模型的形状参数逐渐减小。当油藏个数为25时，模拟的20组形状参数的离散程度很大(β=0.45～1.39)，形状参数中值为0.81；当油藏个数为50个时，20组形状参数的离散程度减小(β=0.59～1.04)，形状参数中值为0.75。随着油藏不断发现，形状参数的离散程度明显减小，形状参数中值也逐渐降低至0.54～0.58附近。

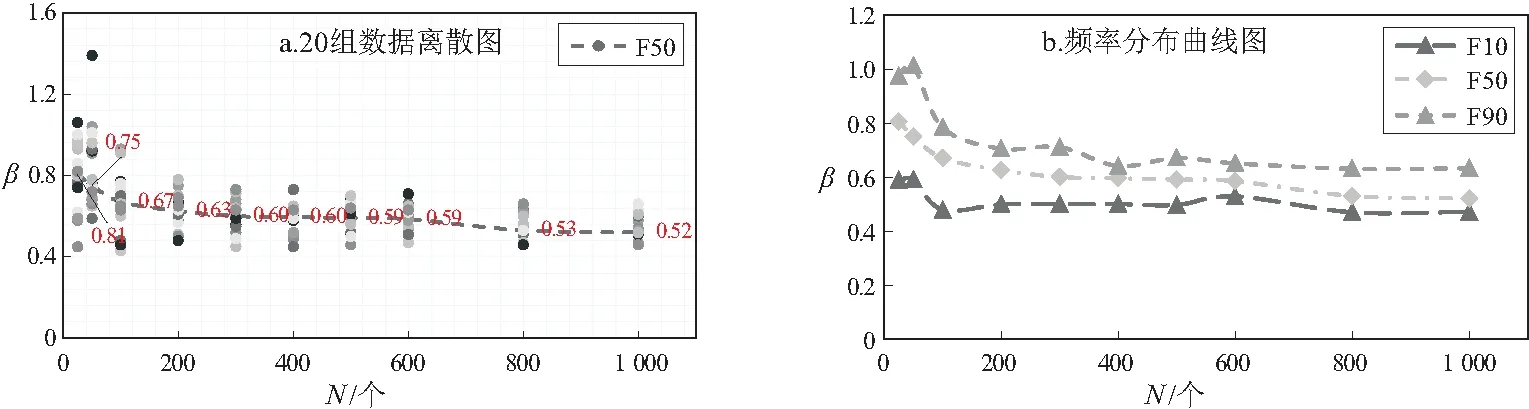
图8 油藏发现个数(N)与油藏规模分布形状参数(β=0.52)交会图

综上，通过对四组不同形状参数的油藏规模分布研究可见，随着勘探的不断进行、被发现油藏个数的增加，其分布模型的形状参数都有稳定的趋势，即β约为0.52～0.55。另外，形状参数分布曲线可以分为两部分：稳定开始点的左边变化趋势，既有稳定下降的，也有先增大再减小的形态；稳定开始点的右边，形状参数基本不再变化。

3.2 分布模型对自然总体分布形状参数(β)敏感性

随着自然总体分布形状参数β(0.41，0.49，0.51，0.52)的变化，绘制油藏分布模型β(F50条件下)随油藏发现个数增长变化趋势图(图 9)。不同的自然总体分布下，趋势图没有明显的区别，说明自然总体的分布对形状参数影响不大，曲线形态整体呈倒“J”形。如前所述，形状参数是随着油藏发现个数增加而减小的，最后趋于稳定。四组数据的形态相似，左侧的下降段形态差异较大，右侧的水平段较稳定。为寻找较为稳定的起始点，绘制了各自的形状参数方差曲线图(图10)，方差的大小可以反映曲线的形态是否稳定。在N<300时，变化比较大，说明曲线的形态不稳定；N>300时，各曲线的方差值都趋近于0，说明此时曲线形态稳定。

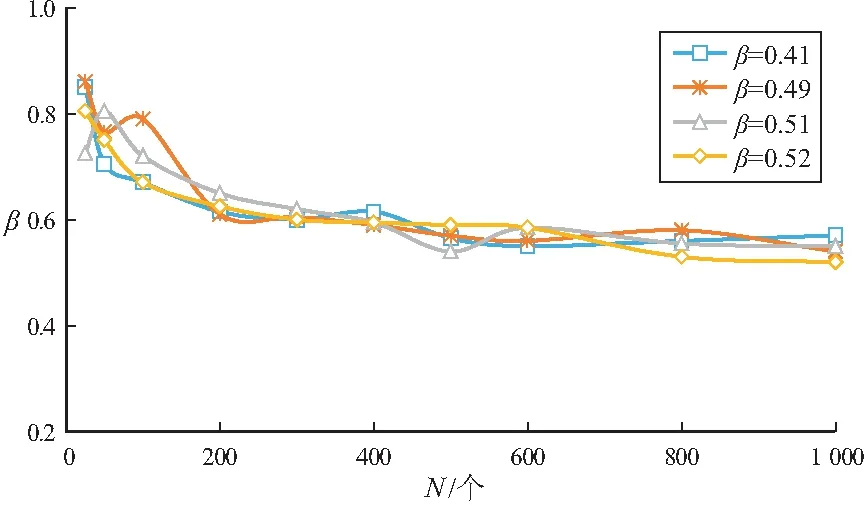
图9 不同自然总体分布形状参数(β)下油藏发现个数(N)分布模型(F50条件下)

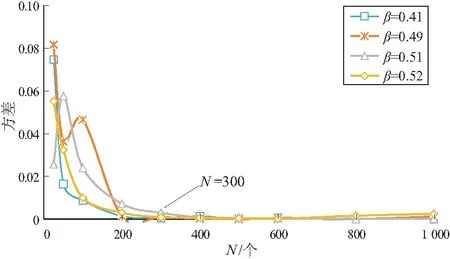
图10 不同形状参数(β)下油藏发现个数(N)分布模型方差曲线图(F50条件下)

3.3 分布模型对自然总体勘探系数(E)的敏感性

敏感性研究是在一种随机的状态下完成的，并未考虑勘探技术的改进和地质认识的提高，这些影响因素又是实际的勘探开发工作中不可避免的，本次研究将这些影响因素称为勘探系数(E)。先进的勘探技术既能推动小油藏的发现，也能增加大油藏的发现概率。在抽样模拟中，表现为2个方面：小油藏个数增加迅速，大油藏增加缓慢；大油藏被发现的概率最大。为了在模拟中体现这种影响，将勘探系数(E)用0～2之间的数值表示，间隔为0.25。以此为基础，选择油藏数目为50、100、300情况下，勘探系数对油藏规模分布模型变化的影响过程；选择β=0.51的数据体进行分析。

3.3.1 油藏预期可发现数目为50

当研究区预期可发现的油藏总数是50个时，分析在不同的勘探系数下，形状参数的变化趋势(图11)。可以看出，每一个勘探系数对应的一组形状参数的离散程度大(β=0.62～0.98)，中值为0.76。随着不同勘探系数的不断增大，形状参数有略微增大的趋势，说明分布模型对勘探系数E的敏感性较小。这可能是大油藏的个数很少，远远小于50个，随着勘探的不断加大，发现的都只是小油藏，而对形状参数的影响很小。

图11 油藏总数为50时勘探系数(E)和形状参数(β)交汇图

3.3.2 油藏发现数目为100

由图12可以看出，每一个勘探系数对应的一组形状参数的离散程度都较大(β=0.57～0.83)，中值为0.69。随着不同勘探系数的不断增大，形状参数有略微增大的趋势，说明分布模型对勘探系数的敏感性较小，原因同上。

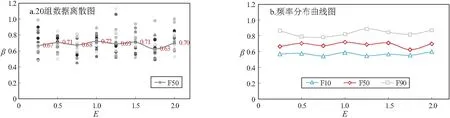
图12 油藏总数为100时勘探系数(E)和形状参数(β)交汇图

3.3.3 油藏发现数目为300

由图13可以看出，每一个勘探系数对应的一组形状参数的离散程度较小(β=0.52～0.72)，中值为0.62。随着不同勘探系数的不断增大，形状参数变化很小，差值在0.01～0.02之间浮动，说明分布模型对勘探系数的敏感性小，原因同上。

图13 油藏总数为300时勘探系数(E)和形状参数(β)交汇图

综上，在N分别为50，100，300下的抽样模拟(图14)发现，形状参数和勘探系数之间存在以下关系：(1)预期可发现的油藏数量越大，形状参数的值减小，因为随着已发现油藏个数的增加，自然总体的形态逐渐被补充完整，而趋近于真实的面貌；(2)在预期可发现的油藏规模相同下，勘探系数对形状参数的影响程度极低，可能是评价单元不同导致的。在常规油气资源评价的过程中，是以单一油气藏为单位的，不同规模之间的油气藏数量级相差很大(能达到100～1 000倍)，而非常规资源评价时将单井EUR作为评价单元，最大的EUR和最小的EUR之间倍数一般不会超过100倍，X230井区约为80倍。这种划分方法将“规模大的油藏”人为剔除掉了，只留下“规模中等的油藏”和“规模较小的油藏”，导致分布模型对自然总体的勘探系数敏感程度很低。

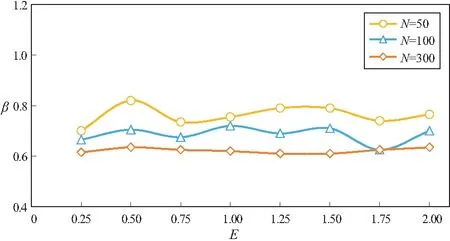
图14 不同油藏发现个数(N)情况下形状参数(β)随勘探系数(E)变化趋势

4 资源量计算

通过对油藏规模分布模型的建立，以及对分布模型的敏感性进行研究，发现在不同的数据体下(β分别为0.41，0.49，0.51，0.52)，发现油藏个数的增加，形状参数整体是呈倒“J”形下降，前面一段下降明显，后一段呈现稳定的趋势(图9)。而勘探系数的提高，其形状参数变化不大，即分布模型对勘探系数不敏感。

油藏规模分布模型其中一个作用就是探究一个区域中油藏的形状参数。形状参数影响着帕累托分布的位置和大小。经过前面分析，油藏规模分布模型的敏感因素只有形状参数，只要确定了形状参数，通过形状参数与油藏个数(N)的交汇图就能推断出油藏的规模分布范围，即可算出研究区的资源量。

在N=300时，处于稳定的状态，所以研究区的可采储量等于300个单井EUR的总和，其平均值为6.72×106t(表2)。采用油气资源丰度法评价X230井区的地质资源量为68×106t，目前鄂尔多斯盆地长7段可采系数约为10%，即可采资源量约为6.80×106t，这与油藏规模分布法计算的结果误差约为1.1%，因此，该方法应用于页岩油评价是可行的。