多因素影响下系统故障预防的多方案比选方法研究*
2022-08-10崔铁军李莎莎
崔铁军,李莎莎
(1.辽宁工程技术大学 安全科学与工程学院,辽宁 葫芦岛 125105;2.辽宁工程技术大学 工商管理学院,辽宁 葫芦岛 125105)
0 引言
系统存在的意义是在预定条件下和预定时间内完成预定功能,即系统实现功能的可靠性。系统可靠性从空间故障树理论[1]来看受到影响因素、元件性质和系统结构的影响。当系统实际运行时,元件性质和系统结构几乎不变,而影响因素的变化则是持续的。所以因素变化对可靠性的影响是确定性和不确定性共同存在的作用。确定性体现在因素变化对可靠性的影响是确定的,而因素变化本身的不确定性导致可靠性变化的不确定。进一步考虑当系统遭遇可预见的环境因素变化时,比如预期内的升温、洪水等事件,系统必将采取有效方案预防事故。那么在众多可用于各因素故障预防和控制的措施中,如何选择适当的措施组成方案完成系统故障预防成为关键问题。方案的选择需要考虑因素、不同措施、措施成本及不采取措施或措施失效的损失成本等。
关于系统安全、可靠性及系统故障预防和解决方案的研究正在大量涌现。这些研究包括考虑风电机组齿轮箱疲劳的风电场可靠性研究[2],二元相关退化系统可靠性分析[3],具有2类失效模式的系统可靠性分析[4],马尔可夫过程的风电系统可靠性分析[5],神经网络的复杂导弹系统可靠性研究[6],半潜式钻井平台系统多状态可靠性分析[7],面向预防性维修的2种失效下多态系统可靠性分析[8],整流侧触发角紧急控制的换相失效预防[9],2种失效的多状态冷贮备系统可靠性研究[10],以及舰船燃气轮机异常响声故障分析[11]等。这些研究在各自领域都较为有效,但它们并未全面考虑上述因素、措施、成本和损失等情况。不具备在系统层面解决上述问题的抽象能力,难以在不同领域对系统故障预防方案的比选形成通用分析方法,导致了多因素、多方案、多措施的成本和损失分析困难。
针对上述问题,本文结合集对分析[12]和空间故障树[1,13]提出多因素影响下系统故障预防的多方案比选方法。赵森烽-克勤概率[14-16]是集对分析创始人赵克勤教授及赵森烽在2014年提出[17]的,其可表示危险事件的发生特征,给出分析方法和实施步骤。本文提出并使用常分量系数与因素分量系数来衡量不同方案实施后可能的系统故障预防效用可靠性及该可靠性的稳定性,从而确定最优系统故障预防方案。
1 集对分析与空间故障树
集对分析理论和方法是研究系统中确定性和不确定性相互作用相互转化的数学理论[17],是由我国数学家赵克勤于1989年提出的,已广泛应用于各领域的确定与不确定性问题分析。
用赵森烽-克勤概率[14-16]来表示各方案对系统故障预防效用的确定性和不确定性。随机事件是具有随机性的事件,是由于2个不同事物在随机事件中同时存在,这2个互不相容事件的相互关系导致了2个事件的随机性[17]。给出随机事件的4个定理,即随机事件成对存在、表现、概率互补和转化定理。这些性质和定理为赵森烽-克勤概率的应用奠定基础,详见文献[17]。
因此集对分析中赵森烽-克勤概率可表示系统不同故障预防方案实施后总成本的确定性与不确定性。同时考虑在空间故障树理论中实施该方法,该理论是研究系统可靠性与影响因素的方法体系,包括空间故障树基础理论[1,13]、智能化空间故障树[18-20]、空间故障网络[21-25]和系统运动空间与系统映射论[26]4部分。核心任务是研究系统可靠性和故障演化过程与因素、事件逻辑关系等的内在联系。因此在多因素影响下可利用空间故障树的基础理论结合集对分析的赵森烽-克勤概率来完成对总成本的确定性与不确定性的描述和研究,从而对多系统故障预防方案进行比选,确定最优方案。其中效用可靠性使用故障预防方案实施后总成本的确定性表征,可靠性的稳定性用总成本的不确定性表征。
同时,根据空间故障树理论对可靠性的研究,认为可靠性是系统需首先保证的,进而保证稳定性。但实际中往往可靠性的稳定性较可靠性本身更为重要。因为低且稳定的系统可靠性可通过系统结构设计提高,但不稳定的可靠性导致无法施加具体措施保证系统可靠性,这是多方案比选的重要原则之一。
2 系统故障预防的多因素多方案比选
设方案比选方法的系统为T={S,F,A},其中S代表方案,S={s1,…,sQ},Q为方案总数,q=[1,Q];F代表因素,F={f1,…,fN},N为因素总数,n=[1,N];A代表危险事件,A={Pc,C,E},Pc代表赵森烽-克勤概率,C代表成本,C={M,L},其中M代表采取措施的措施成本,L代表无措施的损失成本,E代表实施故障预防方案的期望总成本(下文称“故障预防成本”或“成本”)。那么系统的多因素和多方案故障预防比选系统如式(1)所示:
(1)
式中:T为方案比选方法系统;S为方案集合;sq为第q个方案;Q为方案总数;F为因素集合;fn为第n个因素;N为因素总数;A为危险事件;Pc为赵森烽-克勤概率;C为成本;M为采取措施的措施成本;L为无措施的损失成本;E为实施故障预防方案的期望总成本。
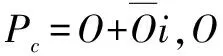
(2)
式中:EF(sq)为故障预防成本;q为方案编号。



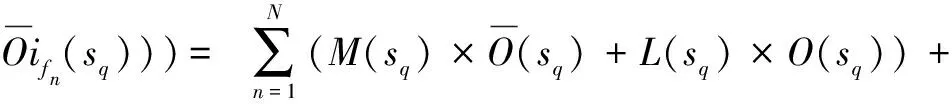
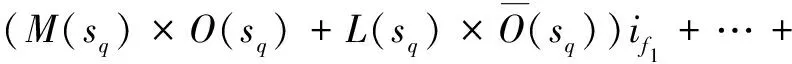
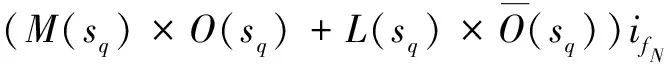
(3)

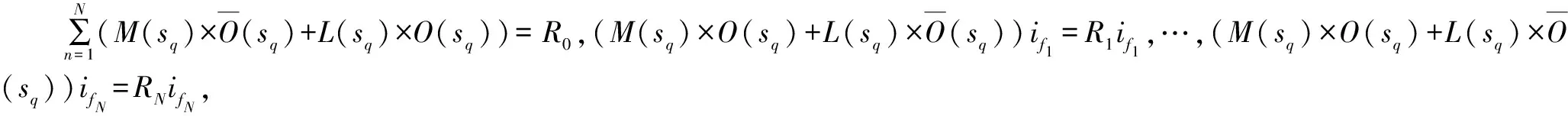
EF(sq)=R0+R1if1+…+RNifN
(4)
式中:R0,…,RN为确定的数值;if1,…,ifN为因素分量的不确定性,ifn∈[0,1]。
式(4)表示对于所有考虑的因素集合F,采取方案sq应对危险事件后的故障预防成本。R0,…,RN为各分量,R0为常分量与因素无关,R1,…,RN为因素分量与因素相关。作为对比确定系统对危险事件不采取措施时的期望总成本EF(U),即考虑所有危险事件情况下的期望总损失成本,如式(5)所示。同时停运方案也是损失成本。
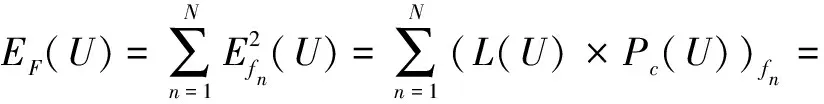

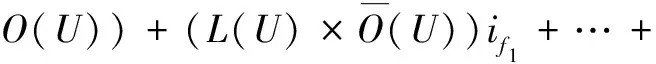
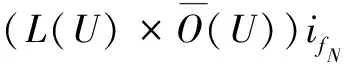
(5)
式(5)也可改写为式(4)的形式。进而将所有方案成本与总损失成本进行对比,将常分量与因素分量分别对比,不同因素各自对应。这些分量的对比结果用分量系数α(sq/U)={α0,α1,…,αN}表示,如式(6)所示:
(6)
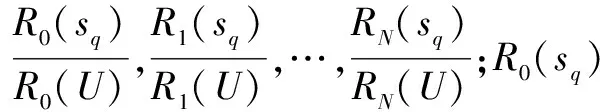
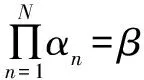
3 实例分析
某电气系统故障受到工作环境中的温度和湿度作用非常明显。同时该系统的工作地点在预期时间内将遭遇高温影响;该地点水系环绕,在高温作用下湿度将明显升高。因此必须对可能出现的高温高湿等危险情况采取系统故障预防方案,分析采取措施和不采取措施带来的故障预防和损失成本。
基本条件:当只考虑温度和湿度对系统故障的影响时,温度升高到35 ℃及以上的概率为30%,升高到40 ℃及以上的概率为2%;湿度升高到90%及以上的概率为21%,升高到98%及以上的概率为1%。
措施方案:
1)系统停止运转预防故障,系统不工作,损失3.5万元;
2)系统采取措施预防故障,系统采取如下4种措施预防事故。
措施①:成本1.9万元,能保障系统在35 ℃及以上时不发生故障,但不能避免40 ℃及以上时系统发生故障,损失5万元;
措施②:成本3万元,能保障系统在35 ℃至40 ℃不发生故障;
措施③:成本1万元,能保障系统在湿度90%及以上时不发生故障,但不能避免98%及以上时系统发生故障,损失3万元;
措施④:成本1.8万元,能保障系统在湿度90%至98%不发生故障;
3)系统不采取任何措施预防故障,考虑系统工作温度和湿度,当在35 ℃及以上时损失为3万元;当在40 ℃及以上时损失为5万元;当在湿度90%及以上时损失为1.2万元;当在98%及以上时损失为3万元。
停止运转和无措施各自独立形成2种方案。采取措施应对温度和湿度且都有2种,因此可得4种方案。将这6种方案组成比选系统T进行研究。
设S={s1,…,s6},s1为停运方案,s2为措施1和措施3,s3为措施1和措施4,s4为措施2和措施3,s5为措施2和措施4,s6为无措施,Q=6。F={f1,f2},f1为温度,f2为湿度,N=2。Pc为各因素导致系统故障的赵森烽-克勤概率,如式(7)所示。M为不同情况下的成本,L为不同情况下的损失。
(7)
式中:↑表示以上,↓表示以下。
方案s1的损失成本E(s1)=3.5万元。
方案s2的故障预防成本,如式(8)所示。
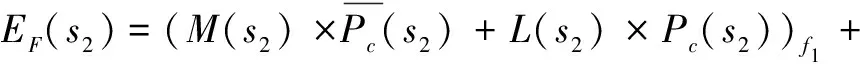



1.9×(0.7+0.3if1)+5×(0.02+0.98if1)+
1×(0.79+0.21if2)+3×(0.01+0.99if2)=
2.25+5.47if1+3.06if2
(8)
同理得到方案s3,s4,s5的故障预防成本分别为EF(s3)=2.834+5.47if1+0.396if2,EF(s4)=2.86+0.96if1+3.06if2,EF(s5)=3.444+0.96if1+0.396if2。如式(5)所示,系统对危险事件不采取行动时的损失成本EF(U)如式(9)所示。
EF(U)=3×Pc(35 ℃↑)+5×Pc(40 ℃↑)+
1.2×Pc(90%↑)+3×Pc(98%↑)=
3×(0.3+0.7if1)+5×(0.02+0.98if1)+
1.2×(0.21+0.79if2)+3×(0.01+0.99if2)=
1.282+7if1+3.918if2
(9)
将各方案成本与不采取措施方案成本的常分量系数与各因素分量系数进行对比,如表1所示,进而对方案进行比选。

表1 不同方案的常分量系数与各因素分量系数对比
s1方案特点是没有因素分量影响,其损失来源于停运带来的经济损失。s6方案特点是系统不停运也不采取故障预防措施,这时系统常分量系数最小,因素分量系数最大,是不采取措施造成的。如果s1和s6方案不可取,需从s2~s5方案进行比选。根据上文给出的比选方法,当常分量系数相差不大时,β最小者为最优方案。
常分量系数代表系统故障预防的可靠性(效用的确定性),而因素分量系数代表了该可靠性的稳定性(效用的不确定性)。不同方案的R0排序s6 1)论述集对分析与空间故障树理论结合的可行性。认为集对分析可处理系统的确定和不确定关系,空间故障树则表征系统的可靠及其稳定性关系,因此它们具有类似结构。系统故障预防效用可靠性可用于故障预防方案实施后成本的确定性表征,可靠性的稳定性用成本的不确定性表征。 2)给出系统故障预防的多因素多方案比选方法和步骤。建立方案比选方法系统,使用赵森烽-克勤概率表示危险事件的发生特征,将措施成本和损失成本与该概率耦合表示各方案的故障预防成本,提出常分量和因素分量及其系数概念用于方案选优。常分量系数代表方案对系统故障预防效用的可靠性,因素分量系数代表该可靠性的稳定性。因素分量系数积越小表明采取该方案系统故障预防的效用不确定性越小。 3)实例分析表明停运方案没有因素分量系数影响,其损失源于停运带来的经济损失。无措施方案的系统常分量系数最小,因素分量系数最大。采取措施的方案中,当常分量系数相差不大时,β最小者为最优方案。4 结论
