高压气瓶快速放气的动态特性研究

齐 超*

（西安航天动力研究所）

0 前言

高压气瓶的快速放气过程广泛存在于能源、化工、航天等领域[1-4]。在高压氢气储运过程中，高压气瓶内氢气的快速充放过程对系统的安全性和经济性有着重要的影响。在火箭和航天飞行器的冷气分离系统中，高压气体往往储存在高压气瓶中，当气体工作时，需先打开阀门，高压气体快速排放到低压容腔内，为分离提供驱动力；高压气瓶的放气速率对分离系统的安全性和可靠性有着重要影响。

高压气瓶快速放气过程中的动态特性，特别是低压容腔和高压气瓶内的压力变化情况是上述系统设计的重要基础。而高压气瓶的快速放气过程为非线性问题，传统的理论分析和数值模拟均有一定的局限性[5-7]。本文对高压气瓶快速放气过程进行了分析，基于物理过程进行了部分简化，建立了理论模型，推导了放气过程中高压气瓶和低压容腔内的压力变化情况；同时开展了验证试验，对理论模型进行了验证。最后基于理论模型对高压气瓶快速放气的动态特性进行了分析。

1 理论模型

高压气瓶快速放气系统如图1 所示，高压气瓶中预先充入高压气体，低压容腔内为真空或常压状态，两者通过管路连接，当控制系统下发放气指令时，连接管路上的阀门打开，高压气体通过管路快速填充到低压容腔中，完成放气过程。放气过程中高压气瓶内的气体温度、压力、密度分别为T1、p1、ρ1；低压容腔内的气体温度、压力、密度分别为T2、p2、ρ2；高压气瓶容积为V1，低压容腔容积为V2。

高压气瓶和低压容腔内的温度、压力、密度等参数均随时间变化，给定阀门打开时刻为0 s。已知初始状态的各项参数，包括高压气瓶初始温度T1（0）、高压气瓶初始压力p1（0）、高压气瓶内气体初始密度ρ1（0）和低压容腔初始温度T2（0）、低压容腔初始压力p2（0）、低压容腔内气体初始密度ρ2（0）。

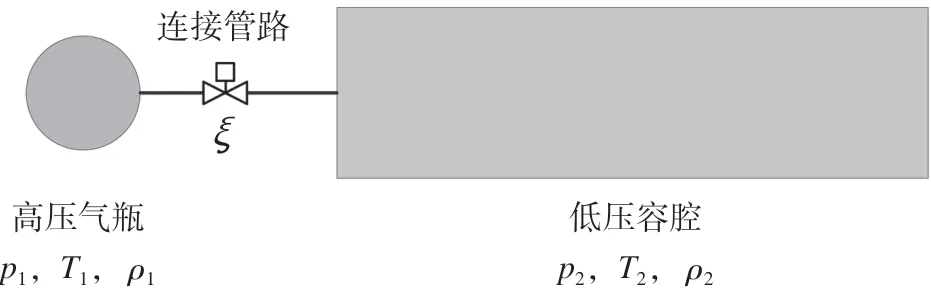
图1 高压气瓶快速放气系统示意图

由连续方程可知，在放气过程中，高压气瓶与低压容腔内气体的质量总量保持恒定（由于管路容积很小，可忽略管路中的气体质量），即：

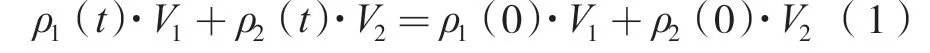
式中：t——时间；

ρ1（t）——高压气瓶内气体密度；

ρ2（t）——低压容腔内气体密度。

放气过程中将气体按照理想气体进行处理，即：

式中：p——气体压力；

ρ——气体密度；

Rg——气体常数；

T——气体温度。

将式（2）代入式（1）中，得：

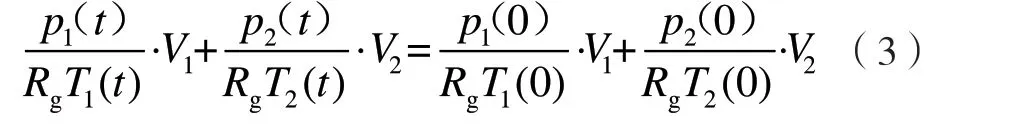
忽略放气过程中的气体温度变化，即放气前后高压气瓶和低压容腔内的气体温度保持一致，即T1（t）=T2（t）=T，则：

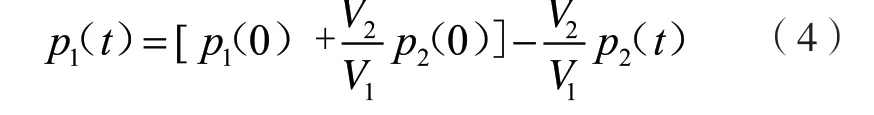
式中：p1（0）、p2（0）、V1、V2——均为常数。

因此，式（4）可简化为：

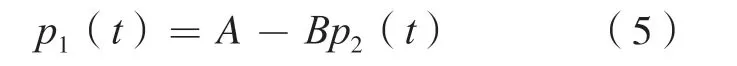
式中：A、B——均为正常数。

高压气瓶向低压容腔的放气过程是由两侧压差驱动的，假设管路系统（包括阀门等）的流动系数为ξ，则：

式中：m2（t）——低压容腔内气体的质量。

由于快速放气过程中的时间很短，压差变化非常大，因此假设流动系数在放气过程中的变化可以忽略，即流动系数ξ为常数。由理想气体状态方程可知：

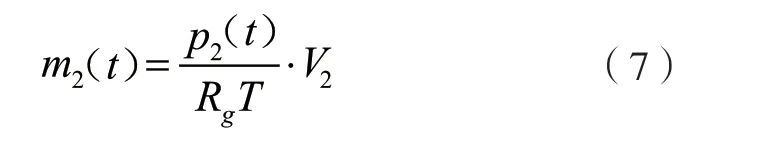
将式（7）和式（5）代入式（6）可得：

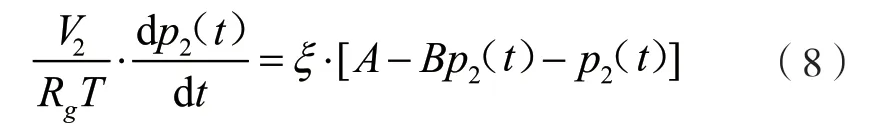
整理后可得：

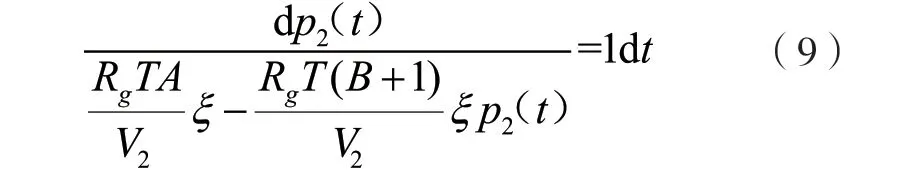
解微分方程式（9）后可得：

式中：C——正常数。

式（10）可进一步简化为：

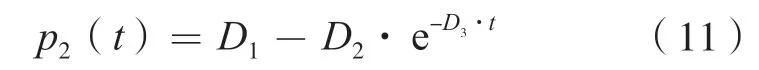
式中：D1、D2、D3——均为正常数。

结合初值条件，各项系数分别表示如下：

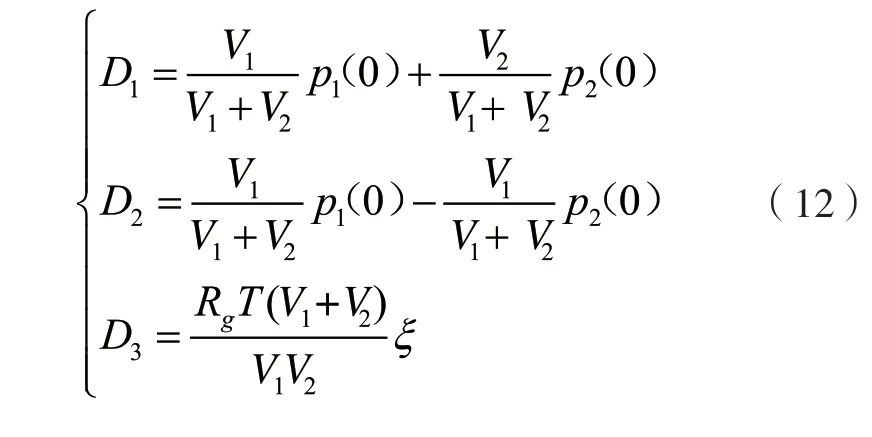
结合式（5）、式（11）和式（12）可以进一步推导出高压气瓶内的压力变化情况。

2 试验验证

为了分析高压气瓶快速放气过程的动态特性，开展了以氮气为介质的放气试验，试验系统如图2 所示。试验系统主要由气源、高压气瓶、低压容腔、系统管路、阀门、压力、温度传感器及数据采集设备等构成。

2 台压力传感器分别用于测量高压气瓶内压力和低压容腔内压力，量程分别为0～30 MPa 和0～0.4 MPa，精度均为0.5%；温度传感器用来测量气瓶表面、容腔内部和表面温度，温度传感器均为T 型热电偶，热电偶的测温范围为-50～100 ℃，精度为1%。

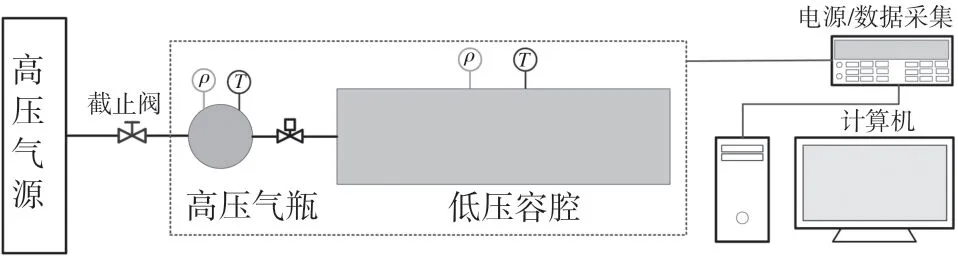
图2 试验系统示意图

试验过程如下：（1）通过高压气源向高压气瓶内充气至要求值p1（0），待气瓶内压力稳定后再补气至p1（0）；（2）通过高压电磁阀打开高压气瓶与低压容腔间的管路，开始快速放气试验；（3）在试验过程中采集并记录温度、压力相关数据，待系统压力稳定后结束试验。

图3 所示为低压容腔内压力在高压气瓶快速放气过程的变化。低压容腔内初始压力为当地大气压（0.094 MPa）；高压电磁阀打开后，高压气瓶内的气体快速充入低压容腔，腔内压力迅速提高，当阀门打开时间达到3 s 左右时，腔内压力基本稳定，此时高压气瓶与低压腔内压力基本相等，不再有气体流入和流出。

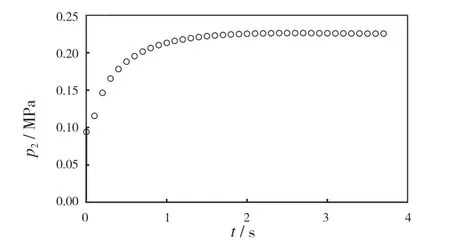
图3 低压容腔内压力变化

试验的各项参数见表1。结合表1 可以计算得到式（11）中的各项系数，其中D1、D2可以通过初始参数和容积比直接计算，D3中的流量系数ξ可以通过试验前后参数来计算平均值；上述3 个系数确定之后就得到了低压容腔内的压力随时间变化函数：

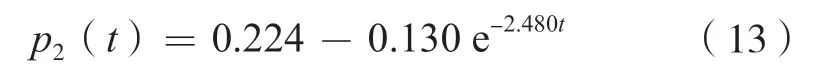
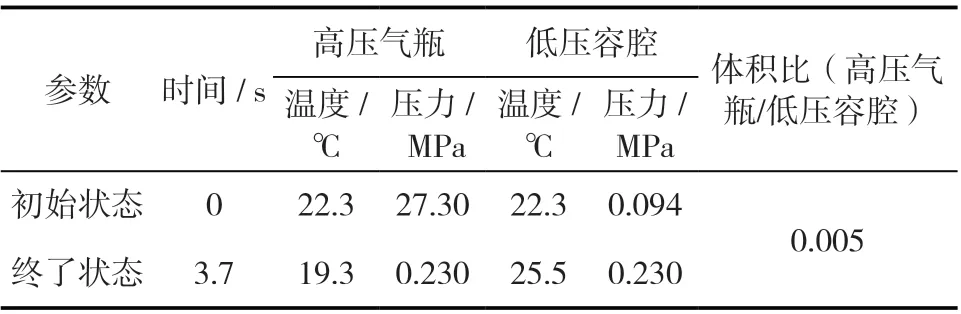
表1 试验参数

低压容腔压力变化的计算结果与试验结果的对比情况如图4 所示。从图4 可以看出，计算结果与试验结果的吻合较好，平均偏差为0.8%。验证了理论模型的准确性和简化假设的合理性。

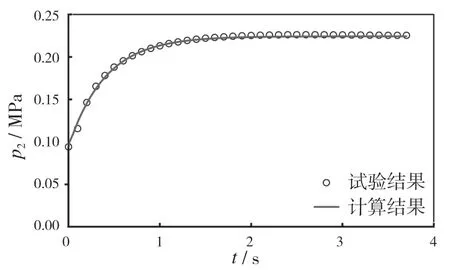
图4 计算结果与试验结果对比

3 动态特性分析

低压容腔内的压力变化如式（11）～式（12）所示。方程中的常数D1和D2仅与高压气瓶和低压容腔的容积、初始状态有关；系数D3还与系统的流量系数，即系统流阻（由管路、阀门以及接口的具体结构决定）相关。

从方程结构和物理过程分析可知，放气过程为典型的惯性过程，随着时间的推移，高压气瓶内压力迅速降低、低压容腔内的压力逐渐提高，两容器间压差即驱动力逐渐减小，因此低压容腔内的压力增长迅速放缓，最终稳定在平衡状态，即：

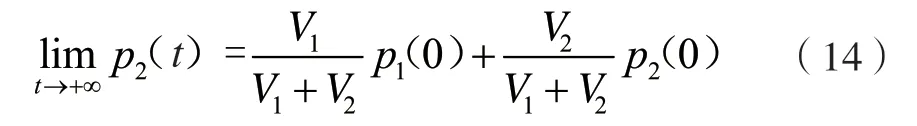
通过式（11）可以看出，当D1增大、D2减小、D3增大时，相同阀门打开一定时间时，低压容腔压力提高，即放气速率提高；结合式（12）分析，当初始参数确定时，提高流动系数ξ，即减小系统流阻（增加管路直径、减小阀门节流等）能够显著提高放气速率。另一方面，可以结合系统要求，通过在连接管路设置减压阀、节流圈等方式来控制放气速率。

4 结论

本文针对高压气瓶快速放气过程，基于实际物理过程和部分简化条件建立了理论模型，推导了高压气瓶和低压容腔内压力变化方程；理论模型计算结果与验证试验结果吻合较好，平均偏差为0.8%。低压容腔的压力变化呈现出惯性环节特征，阀门打开时容腔内压力迅速提高，随着时间增加，压力增长逐渐放缓最终趋于平衡压力。系统流动系数对系统压力、放气速率存在显著影响，当系统管路直径增大、阀门节流减小时，系统流阻减小，流动系数提高，系统的放气速率显著提高。