基于全光谱关联k分布模型的加压富氧燃烧烟气辐射特性研究

周 希，梁 财

(教育部热能转换与控制重点实验室，东南大学能源与环境学院，江苏 南京 210096)

0 引言

燃煤电站作为全世界主要的CO2集中排放源之一，其CO2排放量占全球总排放量的40%以上。近年来，“碳中和(Carbon Neutrality)”、“碳达峰(Peak Carbon Dioxide Emissions)”[1-2]的提出，对能源行业清洁技术的发展提出了更高的要求。燃煤电站CO2近零排放成为研究热点，而富氧燃烧技术是目前最有前景解决该问题的方法之一[3-6]。在富氧燃烧应用过程中，空气分离获得O2及压缩捕集CO2烟气均在高压下进行，一般的燃煤过程却在常压下运行，压力的升-降-升过程造成能量的大量损失，加压富氧燃烧技术克服了能量损失的问题[7]。加压富氧燃烧在高压、高氧含量下运行，烟气成分以水蒸气和CO2为主，此时烟气辐射换热特性与在空气燃烧下差异较大。因此，需要兼顾精度和计算效率的基于非灰体理论的辐射模型对加压富氧燃烧烟气的辐射换热进行预测和描述。基于k分布思想的全光谱k分布模型兼顾计算精度与计算效率，其中全光谱关联k分布模型对非均匀介质具有更高的精度，在整个光谱内对吸收系数进行积分，通过较少的计算得到总辐射热流和辐射源项，且可以和不同的辐射传递方程的求解方法结合，可同时处理散射问题。

FSCK气体辐射模型假设某个热力学状态与另一个热力学状态下吸收系数存在相关性，利用高精度的求积格式进行光谱积分，在不损失光谱精度的前提下大幅减少辐射传递方程(Radiative Transfer Equation, RTE)的求解次数。对于均匀介质，FSCK有着极高的精度；对于非吸收性主导的非均匀介质，FSCK的计算精度LBL计算结果十分接近[8-9]。Modest[10]提出了基于k分布思想的全光谱关联k分布理论，该理论的提出扩大了k分布在非均匀气体介质辐射领域的应用范围。Liu[16]等研究了不同气体辐射FSCK方法中相关k值的求解方法，得出了按高低温区域分界的相关k值求解方法。Zhou等[11]利用多层神经网络(MLP)开发了基于机器学习的气体介质FSCK数据库，该数据库大幅压缩了大小，同时保持了相似的精度和效率。迄今为止，全光谱关联k分布的提出与发展极大地推动了非均匀气体介质辐射特性的研究，但目前FSCK模型集中于气体混合物辐射特性的研究，粒子辐射特性常用模型较为复杂。因此，对于含有气体和粒子的吸收散射性介质的辐射传热，难以将气体与粒子的辐射特性参数进行有效的耦合处理，导致气体与粒子混合物的辐射传递方程在求解过程中面临计算效率低等问题，亟需建立一种适用于加压富氧燃烧气氛的吸收散射性介质全光谱关联k分布模型。

本文在FSCK模型的基础上，构建适用于加压富氧燃烧气氛下的非均匀气体介质FSCK模型，并与LBL及WSGG模型对比验证其计算精度和效率，探究加压富氧燃烧下气体介质的辐射传热特性；基于该FSCK模型，利用Mie理论描述加压富氧燃烧气氛下烟气中粒子的辐射特性，建立基于k分布的吸收散射性介质辐射特性模型，揭示加压富氧燃烧下包含飞灰颗粒的烟气辐射传热特性。

1 辐射传热理论及全光谱关联k分布模型构建

1.1 气体全光谱关联k分布模型

对于具有发射、吸收、散射及各向异性的介质，在空间中的辐射传递方程可表示为[15,17]

(1)

式中I(s,s)——方向s处s位置的辐射强度；

κga——介质中气体组分的吸收系数；

κpa——介质内部粒子的吸收系数；

σs——粒子的散射系数；

Ib(s)——介质在位置s处的黑体辐射强度；

Φ(s,si)——散射相函数，能量从入射方向si散射到出射方向s的部分；

Ωi——立体角。

在非均匀混合物中，某一光谱变量可以根据参考状态φ0的吸收系数进行重排，可得到在参考状态φ0及参考温度T0下的全光谱k分布

(2)

式中 前两项所涉及的近似是关联原理[22]的数学表达；

η——波数；

kη——光谱吸收系数；

δ(·)——狄拉克-德尔塔函数；

Ib和Ibη——普朗克函数和光谱普朗克函数；

g——吸收系数小于局部k值的光谱部分;

φ0与T0——参考状态与参考温度;

φ——局部状态。在参考状态φ0下，忽略了散射项的RTE经过重排可表示为

(3)

式中k*——相关k值，累积全光谱k分布为

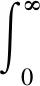
(4)

此外，非灰拉伸函数为

(5)

1.2 吸收散射性介质FSCK模型

Mie理论对于粒子辐射传热能够提供很高精度的计算结果，但是Mie理论计算效率较低，且无法与气体介质的辐射传热进行耦合求解。因此，需要建立一种能耦合处理气体与粒子辐射特性参数的辐射模型。考虑到加压富氧燃烧的热力学环境及该环境下飞灰颗粒的化学性态，0.2～20 μm的波长范围已满足计算要求，并在整个光谱上划分22个区间[21]。假设研究的粒子为稀疏粒子系，粒子之间为独立散射，粒子系的吸收和散射系数为单个粒子的代数和[15,17]。基于气体吸收系数的k分布原理，分别进行粒子的吸收系数及散射系数全光谱关联k分布模型的建立。假设粒子由两种不同介质混合，对其吸收系数和散射系数在整个光谱上重排，得到吸收系数和散射系数的累积k分布函数库。确定粒子粒径与体积分数后，吸收与散射系数为定值，只需建立吸收因子与散射因子的累积k分布函数，可表示为

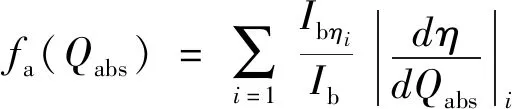
(6)

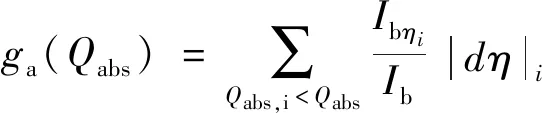
(7)

通过引入k分布的思想，并借鉴气体的全光谱关联k分布模型，将式(1)两边乘上狄拉克-德尔塔函数δ(·)在整个光谱上的积分，并除以几率分布函数f(k)，吸收散射性介质的RTE可以改写为

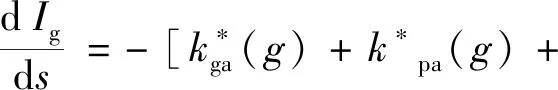
(8)

基于该吸收散射性介质FSCK模型可以有效地耦合介质内部气体与粒子的辐射特性参数，方便地求解吸收散射性介质的辐射传递方程。

2 结果与分析

2.1 全光谱关联k分布模型的验证

为了验证FSCK模型计算混合气体辐射特性的精度及效率，以加压富氧燃烧烟气中H2O和CO2组分为对象，研究了一维平行平板组成的封闭系统内混合气体的辐射热流与辐射源项，其中壁面为冷温黑体的边界条件，并将计算结果与LBL、WSGG的解进行对比[12-13]。设置了两种不同的工况，具体参数详见表1。s表示坐标参数；L表示板间距，L=1 m；x(·)为物质的摩尔分数。

表1 不同工况下的热力学参数

图1为不同工况下，使用三种气体辐射模型计算得到混合气体的辐射热流和辐射源项，实线表示三种模型计算得到的辐射热流和辐射源项分布，虚线表示FSCK和WSGG与LBL计算结果的相对误差，相对误差由式(9)计算得出

(9)

由图1(a)和(b)可知，对于等温均匀的工况，FSCK计算得到的混合气体辐射热流与辐射源项分布都与LBL计算结果十分接近，辐射热流的最大误差出现在介质内部，为9.97%；辐射源项的最大误差也出现在相同位置，为18.06%。WSGG辐射热流与辐射源项分布与LBL差异较大，相对误差均在40%以上，尤其是在近壁面处，相对误差达到最大，约为60%和80%。图1(c)和(d)为在非等温非均匀的气氛下气体辐射特性，FSCK与LBL的计算结果具有很高的贴合度，辐射热流的最大误差在15%左右，辐射源项的最大误差约为40%。当局部温度从低于参考温度的区域上升到高于参考温度的区域时，FSCK模型中的非灰拉伸函数α变化较大，并且FSCK模型忽略了温度对关联吸收系数k*求取方式的影响同样导致了误差的产生。在实际工业的热力学计算中，辐射热流是传热研究的重点对象，鉴于该工况下FSCK的辐射热流计算结果仍有着很高的精度，因此FSCK适用于加压富氧燃烧下辐射换热计算。而在相同条件下WSGG辐射热流分布的相对误差在50%以上，辐射源项的最大相对误差为80%左右。表2为辐射热流与辐射源项的平均相对误差，FSCK两工况误差控制在10%以内，WSGG两工况的平均误差均在50%左右。因此，FSCK模型辐射传热的计算精度比WSGG高很多。

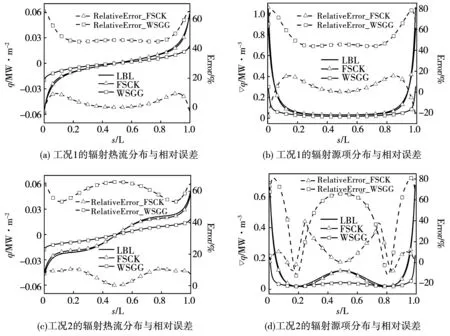
图1 不同气体辐射模型下混合气体的辐射传热特性

表2给出了三个工况下不同气体辐射模型的计算效率，计算采用的CPU为Intel(R) Core(TM) i7-10700，由式(10)定义了FSCK和WSGG相较LBL提升的计算效率

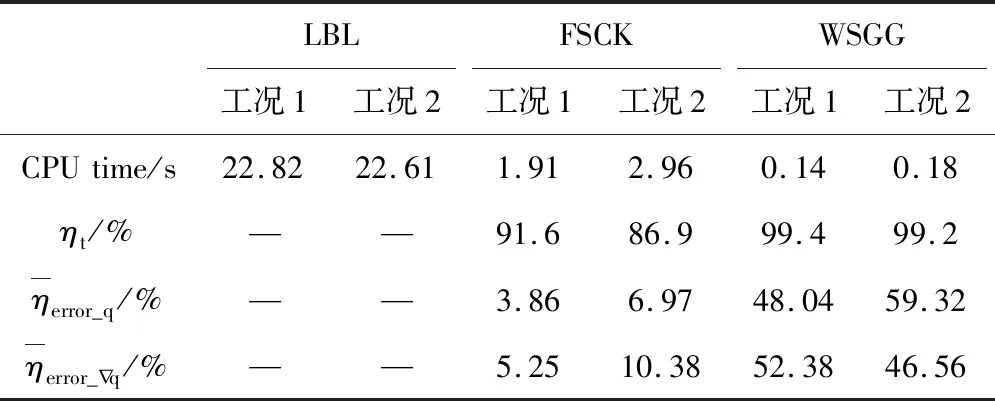
表2 FSCK与WSGG在不同工况下计算效率与计算精度

(10)

FSCK与WSGG在两个工况计算效率的提升都在90%左右，FSCK最高可达到91.6%，WSGG的效率提升接近100%。虽然FSCK的计算效率比WSGG稍低，但计算精度要高很多，因此FSCK模型在研究富氧燃烧烟气辐射特性领域具有更大的计算优势。

综上所述，利用FSCK模型处理混合气体的辐射传热问题，在损耗较小的计算效率下，计算结果可保持很高的精度。

2.2 基于吸收散射性介质FSCK的烟气辐射换热特性研究

在工业生产中，加压富氧燃烧条件下炉膛内由于运行压力的升高，高温烟气中的H2O和CO2浓度大大增加，烟气的密度增大。烟气组分中参与辐射的不仅有CO2和H2O等具有吸收性的三原子气体介质，烟气中还裹挟着大量的未燃尽碳颗粒、灰分和烟黑颗粒，这些粒子通过吸收、散射和发射辐射参与辐射传热过程。大量研究表明，煤等固体燃料形成的烟气产物中，粒子辐射占主要地位[28]。因此，在研究加压富氧燃烧下烟气的辐射传热特性时，需着重考虑粒子辐射对烟气整体辐射特性的影响。但在工程应用中，粒子的光谱辐射特性采用类似气体逐线法模型的思想进行计算，处理起来非常复杂，效率较低，难以在工程上大规模应用，本文通过建立的吸收散射性介质的FSCK模型，探究加压富氧燃烧下混合烟气的辐射传热特性。

表3和表4给出了三种不同的工况及粒子浓度。图2分别为不同粒子浓度下，常压富氧燃烧、常压空气燃烧及加压富氧燃烧气氛下混合烟气的辐射源项分布。结果表明，当粒子浓度为0时，三种不同燃烧气氛的辐射热流与源项分布具有明显的差异：空气燃烧下由于具有辐射能力的介质含量较低，介质内部的辐射换热明显弱于富氧燃烧下的辐射换热；高压使得介质辐射换热较常压环境下更为强烈。当粒子浓度为10-5时，三种工况下的辐射热流或辐射源项分布之间开始出现相互靠拢的趋势，如图2(b)所示，工况3与工况4的辐射源项分布相比粒子浓度为0时更加接近；当粒子浓度为10-4时，上述变化趋势更为明显，由图2(c)可以发现，工况3与工况4的辐射源项分布更吻合。此外，通过对比前三组辐射源项分布图可以发现，在粒子浓度偏低的情形下，不同粒子浓度下的烟气辐射源项分布变化十分细微，三种燃烧气氛下辐射源项的最大值均在1.5 MW/m3、0.5 MW/m3、0.25 MW/m3左右，此时粒子的存在对烟气辐射未产生明显的影响。当粒子浓度增大到3×10-3时，如图3(d)所示，三种气氛下烟气的辐射热流与源项分布几乎相同，其源项的最大值均约为3.5 MW/m3，并且此时源项远远大于另外三种粒子浓度下的源项。由此可知，此时烟气的辐射特性几乎不受燃烧气氛变化的影响，即粒子辐射在烟气整体辐射中占主导地位。因此，对于含有高浓度粒子的燃烧环境，如流化床飞溅区及流化床稀相区，粒子的性质基本决定了烟气的辐射特性。

表3 加压富氧燃烧气体参数

表4 飞灰颗粒的浓度

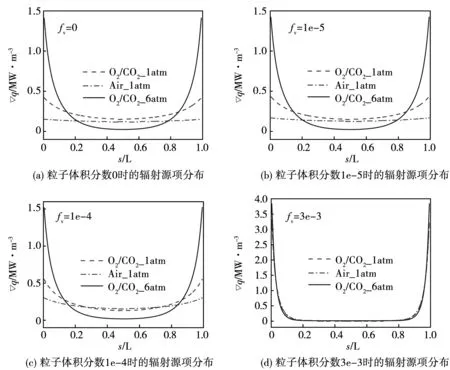
图2 粒子浓度对加压富氧燃烧均温均质烟气辐射传热特性的影响

3 结论

本文在全光谱关联k分布模型的基础上，构建了适用于加压富氧燃烧气氛下的非均匀气体介质的FSCK模型，验证了其辐射换热的计算精度与计算效率，并探究加压富氧燃烧下气体介质的辐射传热特性；基于本文建立的加压富氧燃烧气体FSCK模型，结合Mie理论来描述加压富氧燃烧气氛下烟气中粒子的辐射特性，建立了吸收散射性介质的全光谱关联k分布模型，揭示了加压富氧燃烧下包含飞灰颗粒的烟气辐射传热特性。结论如下：

(1)对于不同工况，FSCK计算耗时比WSGG稍多，但计算效率的差距不大。FSCK获得的辐射热流与辐射源项与LBL高度吻合。因此，FSCK在损耗较小计算效率的前提下，具有很高的计算精度，适用于研究加压富氧燃烧条件下混合气体的辐射传热特性。

(2)基于本文建立的吸收散射性介质全光谱k分布模型，有效预测了粒子辐射对烟气辐射的影响。在低粒子浓度下，烟气气体成分对烟气整体辐射特性有着一定的影响，此时气体辐射在混合烟气中具有重要的影响。在高粒子浓度下，烟气的气体组分和总压对烟气的辐射热流与辐射源项影响较小，粒子的存在对烟气辐射换热产生了强烈的影响。利用本文建立的吸收散射性介质全光谱k分布模型对非等温非均匀烟气混合物的辐射换热进行研究，进一步论证了高粒子浓度下粒子的辐射特性对烟气辐射换热起决定性作用，并验证了该模型的有效性。