基于ARIMA 模型的贵州省GDP 分析与预测

张 梓

（贵州大学 经济学院，贵州 贵阳550025）

0 引言

GDP 是国民经济核算的核心指标，也是衡量一个国家或地区经济状况和发展水平的重要指标。改革开放四十多年来，贵州牢牢抓住机遇，全力开展经济建设，地区生产总值保持平稳快速发展。党的十八大以来，贵州发展进入“黄金十年”，经济增速连续十年位居全国前列，经济总量全国排名由第26 位提升至20位，取得了举世瞩目的巨大成就。“十四五”时期是我国社会主义现代化建设的重要阶段，贵州将如何保持现有经济增速，推动贵州高质量发展，同时在复杂多变的宏观经济环境下，对政府决策机构把握未来的经济发展趋势做出正确决策和规划具有重要现实意义。

当下对GDP 的预测主要通过计量经济学模型、机器学习模型和灰色系统理论来实现。例如，张延群等[1]利用柯布- 道格拉斯生产函数和Solow 增长模型分阶段预测了中国未来的经济增长；张自敏等[2]就广西GDP数据采用改进的BP 算法有效证明了该模型预测精准性的提高。其中ARIMA 模型自1970 年提出以后，在时间序列分析领域得到了广泛的应用，是预测GDP的常见方法。众多学者运用ARIMA 模型在上海（冉德欣[3]）、云南（郑伟等[4]）、浙江（郑梦琪等[5]）、陕西（王芳芳等[6]）、重庆（高炎[7]）、湖南（王鄂等[8]）等省域层面开展了针对其GDP 的分析和预测，均具有较高的精度，预测效果良好。高炎[7]利用eviews 9 建立ARIMA(0,1,1)模型在一定误差范围内准确预测了重庆市未来三年GDP；魏宁[9]和王芳芳等[6]利用SPSS 软件分别对陕西省1952—2007 年和2000—2018 年的GDP 分析建立ARIMA 模型，预测陕西省GDP 将保持较高增长趋势，预测结果比较理想；王鄂等[8]采用不同的预测方法对湖南省GDP 进行预测，得出ARIMA(1,1,2)的预测相对误差比Holter-Winter 模型预测误差小，从而建立最优ARIMA(1,1,2)来预测湖南省GDP。但是，针对贵州省的GDP 预测则较为鲜见。在贵州省经济增长“黄金十年”的发展话语下，本文将利用Python 软件，选取贵州省1978 年至2020 年的GDP 年度数据建立ARIMA 模型，对其短期GDP 展开高精度预测，在宏观经济规划层面具有重要意义。

1 ARIMA 模型的基本原理

ARIMA 模型是由自回归模型（AR）、移动平均模型（MA）和差分法结合而来的时间序列预测模型。若序列是一个平稳时间序列，则该模型是一个具有p 阶自回归和q 阶移动平均的混合模型，用ARIMA (p,q)表示，实际中的许多经济序列是非平稳时间序列，要进行差分d 为差分次数。将其变为平稳后，它的行为并不会随着时间的推移而变化，那么我们就可以通过该序列过去的行为来预测未来。对于这样的模型我们称为整合的ARIMA模型，记为ARIMA(p,d,q)。

2 基于ARIMA 模型的实证分析

2.1 数据预处理与初步分析

为保证数据的可靠性，所选取的贵州省GDP 数据全部来源于《贵州省统计年鉴》。分析贵州省GDP 数据可以得出，自1978 年我国实行改革开放以来，贵州省经济实现巨变。2020 年，贵州省地区生产总值达到17 826.56 亿元，与1978 年的46.63 亿元相比增长了近382 倍，经济总量实现了历史性的飞跃。同时观察贵州省地区生产总值数据的时间序列图（图1）可以看出改革开放四十多年来，贵州省GDP 总体上呈现指数式的增长，经济实现了波澜壮阔的大发展，地区生产总值占全国比重不断提高。

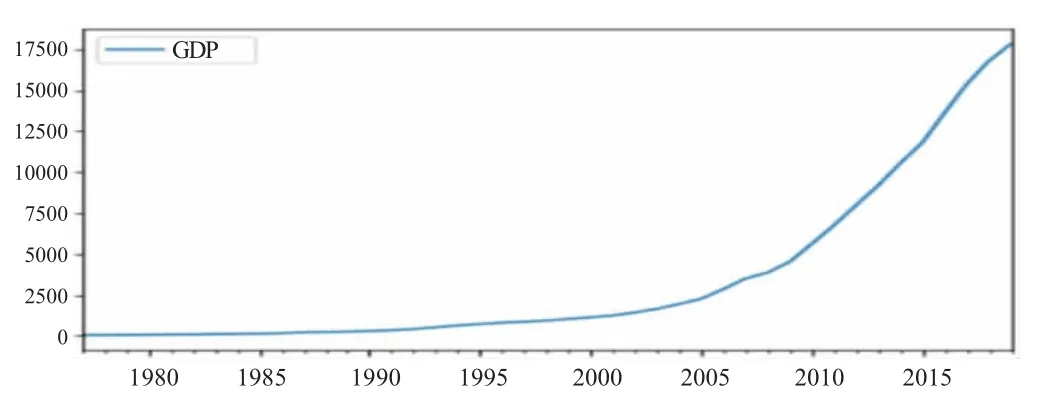
图1 贵州省1978—2020 年GDP 折线图

2.2 平稳性检验

平稳性检验通常采用观察自相关图的方式来初步判断序列的平稳性，或者直接对序列进行单位根检验。画出GDP 数据的自相关图后通过图形可以初步判断原序列为非平稳序列，然后利用Python 软件进行adf_test 得到GDP 序列的p_value=0.994 接受原假设，说明原序列不是一个平稳序列。

2.3 对数一阶差分

通过上一步骤的平稳性检验可知贵州省GDP 时间序列不是一个平稳序列，并且观察数据序列图发现GDP 呈现指数增长，因此首先利用Python 软件中numpy 函数对数据进行对数处理，随后进行一阶差分，差分后的时间序列基本符合平稳时间序列特征，围绕固定值上下波动。对处理后的平稳序列进行单位根检验，得到p_value=0.006 6，有充分理由拒绝原假设。因此贵州省GDP 进行对数一阶差分后的序列为平稳序列，可以进行下一步骤的操作。

2.4 ARIMA(p,d,q)的识别

模型的识别主要依靠分析自相关图和偏自相关图将原序列数据通过取对数和一阶差分处理变为平稳序列之后，利用Python 软件分别画出自相关图与偏自相关图，观察图形的自相关系数的变化趋势可以初步判断p、q 的取值。从图2 可以观察到序列的自相关图在第1 阶之后急速衰减，自相关图呈现一阶截尾的状态，因此q=1。而图3 偏自相关图在滞后十几阶相关系数仍显著不为零，呈现拖尾衰减特征，因此p=0。

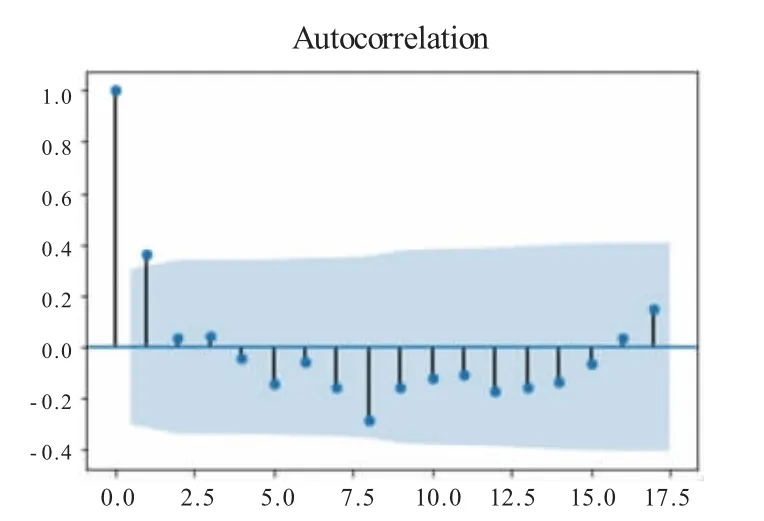
图2 自相关图

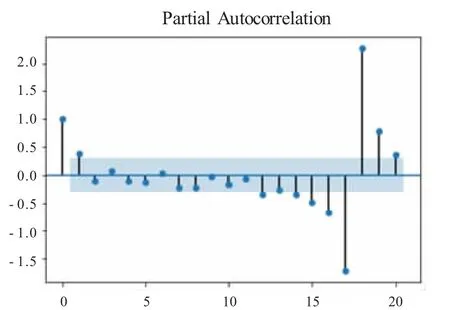
图3 偏自相关图

为了保证p、q 值的选择更加准确合适，利用Python 软件中pmdarima 库中auto_arima 函数进行模型拟合，得到ARIMA (0,1,1)、ARIMA(1,1,1)、ARIMA(0,1,2)、ARIMA(2,1,2)等不同参数下AIC 得分，分别为-138.820、-136.847、-136.847、-132.869。其 中 模 型ARIMA(0,1,1)对应的AIC 值是最小的，为-138.820。因此拟合最好的模型为ARIMA(0,1,1)。

2.5 残差白噪声检验

得到估计的模型之后，为了确定该模型是否完全反映了序列中有价值的信息，是否是有效的，需要对模型的残差序列进行白噪声检验。本文利用Python 软件画出残差序列的分布图，Q-Q 图，以及自相关图,观察Q-Q 图中点可以看到近似的落在一条直线，即红线。可以初步判断残差序列是随机的正态分布，得出结果是不存在自相关性。

为了得出更准确的结论，利用Python 软件中acorr_ljungbox 对残差序列进行白噪声检验，并画出白噪声结果（图4），分析图4 可得p-value 值大于0.05，即使在滞后多期时在95%的显著性水平下的接受原假设，即ARIMA(0,1,1)模型的残差序列为白噪声序列。说明序列中几乎所有有用信息都被此模型提取反映出来，拟合的ARIMA(0,1,1)模型可以作为理想的预测模型。

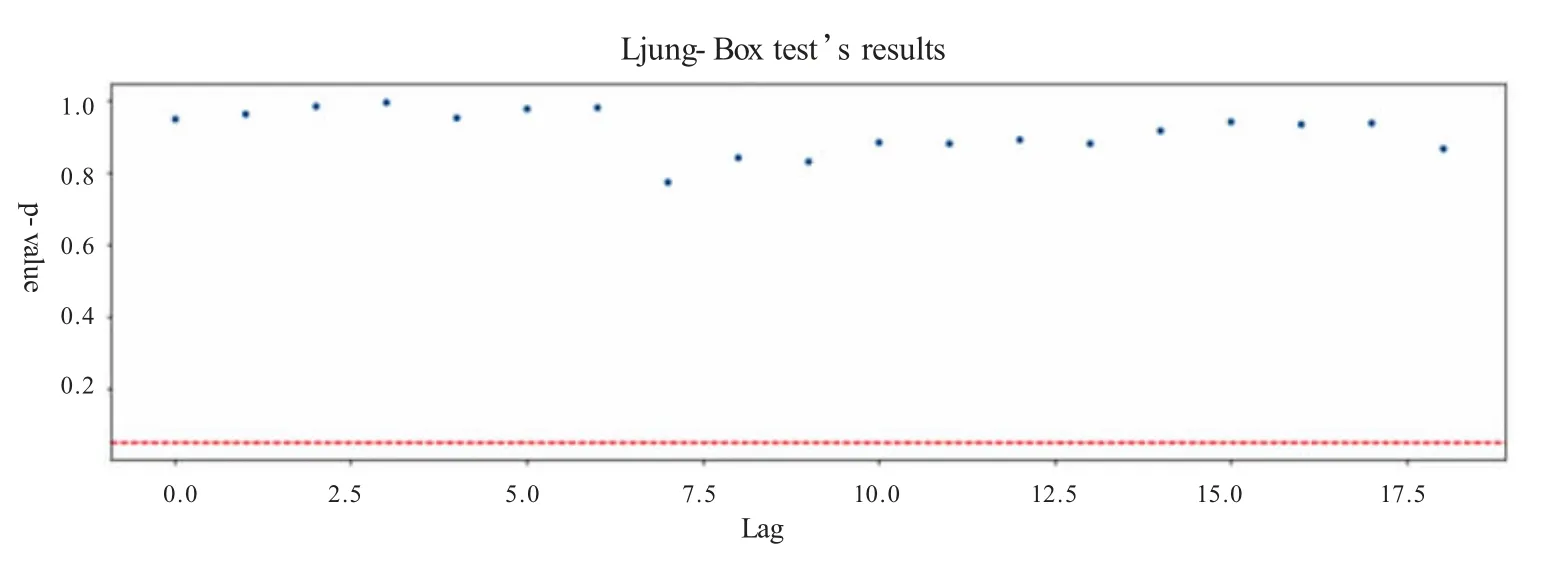
图4 白噪声检验结果

2.6 参数显著性检验

利用Python 软件对模型的参数进行显著性检验，结果显示，在模型ARIMA(0,1,1)下得到模型参数系数分别为Ma1: 0.431 3、const：0.141 4。显著性分别为Ma1:0.002、const:0.000。参数统计量在95%的置信区间内p_value 值都小于0.05，即所有系数都通过显著性检验。

2.7 模型预测

利用上述建模步骤建立的ARIMA(0,1,1)模型对贵州省的GDP 进行预测，将预测结果和贵州省GDP 的实际值对比并利用作图软件画出趋势图（图5）。可以清楚地观察到贵州省GDP 的预测值与实际值基本处于同一位置上，误差较小，在可以接受的范围内，证明所构建的模型ARIMA(0,1,1)是有效的，可信的。

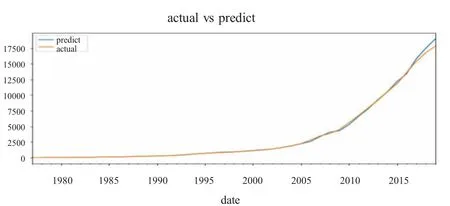
图5 真实值与预测值比较

将利用ARIMA(0,1,1)模型预测的贵州省2016—2020 年地区生产总值与实际值进行详细的对比，对比结果如表1 所示。经过详细计算得到贵州省2016—2019 年的GDP 预测值与实际值之间的相对误差值，结果精确到小数点后三位，通过结果可以得出模型预测的误差控制在较低的范围内，均不超过0.05。但是2020 年的相对误差超过了0.05，经过分析可能是因为2020 年新冠疫情的爆发使得2020 年年初的经济处于较低的增长水平，甚至负增长。但总体来看相对误差还是处于低水平，可以有理由相信使用建立的模型来预测贵州省未来的GDP 是可靠的。

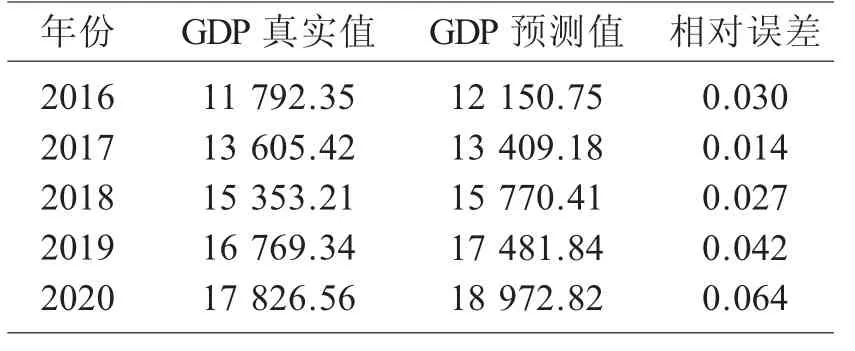
表1 贵州省2016—2020 年GDP 真实值与预测值数据比较

由此可以利用此模型对贵州省未来五年的GDP做出预测，预测值如表2 所示。可以看出“十四五”时期贵州省GDP 仍然保持较高的增长速度，到2025 年地区生产总值将达到一个新的台阶。

表2 贵州省2021—2025 年GDP 预测值

3 结论

本文采用贵州省1978—2020 年的地区生产总值数据进行时间序列分析，利用Python 软件画出自相关图并进行单位根检验，可以判断该GDP 数据为非平稳序列，因此对原序列进行对数和一阶差分处理，处理后的时间序列通过ADF 检验达到平稳。并进一步分析序列的ACF 和PACF 图的拖尾和截尾情况，初步判断模型的p、q 取值，根据AIC 准则判断最佳模型为ARIMA(0,1,1)。然后对模型的残差序列进行白噪声检验，结果显示残差序列为白噪声序列，说明模型充分解释了数据中的信息，具备有效性。因此，本文利用该模型对贵州省2016—2020 年的GDP 进行预测，预测值与实际值在2020 年误差为0.064，一个可能的解释是重大突发疫情的蔓延给经济发展带来了较大的不确定性。其余年份预测值和实际值误差都控制在0.05的范围内，预测结果与实际较为符合，模型的可信度较高，较为准确地预测了贵州省未来五年（2021—2015）的GDP，依次为19 989.63 亿元、23 025.79 亿元、265 233.10 亿元、30 551.60 亿元、35 191.97 亿元，从数据上看继续保持着较高的增长趋势，可以为政府经济决策提供一定的参考依据。