车辆荷载作用下超大断面双层隧道动力响应分析
2022-08-09李超凡
李超凡
(安徽巢湖路桥集团有限公司, 安徽 巢湖 238000)
随着中国经济的快速发展和交通运输量的不断增加,公路等级要求不断提高,三车道大断面公路隧道相继涌现。国内对车载作用下大断面铁路隧道的动力响应研究颇多,而对公路隧道动力响应的研究少见。该文依托温州大罗山大断面双层结构隧道工程,研究运营期车辆荷载作用下隧道结构的动力响应,为隧道结构的疲劳损伤研究与健康监控提供依据。
1 工程概况
温州环山北路项目大罗山隧道左线长1 360 m,右线长1 430 m。开挖高度13.8 m,开挖宽度16.52 m,标准开挖断面172 m2,最大开挖截面200.49 m2。为上下双层对称四心卵形结构,上层设置为三车道机动车道,下层为非机动车道、人行道和通风管线通道。该隧道为扁平结构,结构新颖,工艺复杂,施工技术难度高,二次衬砌砼浇筑难度大。这种隧道结构国内罕见,也是国内首座采用钻爆法施工的双层扁平结构隧道。
2 动力响应计算原理
2.1 车辆荷载模型
由于实际车辆荷载复杂多变,数值分析时采用简化模型,较常见的有均布恒载、移动恒载、波动荷载3种。均布恒载、移动恒载模型将荷载作为恒载考虑,而车辆实际行驶中荷载作用位置和大小均随时间不断变化,故将车辆轮胎荷载近似简化为路面集中点源荷载,采用波动荷载的简化模型。
将车辆荷载转化为大小与作用位置均随时间以波动形式作用在路面上的半正弦荷载,这种半正弦荷载对路面某一点的力学作用数学表达式为:
F(t)=p+q(t)
(1)
式中:p为恒载,其大小等于轮压;q(t)为附加动荷载。
2.2 边界条件
较成熟的人工运动边界主要有黏性边界、叠加边界、旁轴边界、黏弹性边界、一致边界、透射边界和动力映射边界等。基于一维波动理论的一维黏弹性局部人工边界具有概念明确、运用便捷等优点;基于柱面波动方程的二维黏性人工边界解决了一维局部人工边界低频漂移的问题,且具有较好的高、低频稳定性;基于三围球面波理论的三围时域黏弹性人工边界能对无限域介质中的波动进行模拟分析,计算更方便、可靠。这里采用黏弹性边界,其一般表达式为:
σli(t)=-Kliuli(t)-Cliu′li(t)
(2)
式中:下标l为人工边界节点号;下标i代表分量方向,i=x,y,z;t表示时间;σli(t)、uli(t)、u′li(t)分别为节点l方向i的应力、位移和速度;Kli、Cli为节点l方向i的黏弹性边界参数,是无限域介质的材料常数和边界尺寸的函数。
2.3 数值计算方法
模型计算中采用的动力平衡方程为:
[M]u″(t)+[C]u′(t)+[K]u(t)=P(t)
(3)
式中:[M]为质量矩阵;[C]为阻尼矩阵;[K]为刚度矩阵;P(t)为动力荷载;u(t)、u′(t)、u″(t)分别表示相对位移、速度、加速度。
采用Rayleigh阻尼表示隧道结构体系的阻尼机制,即假定体系阻尼与刚度矩阵、质量矩阵成比例,其数学表达式如下:
C=αM+βK
(4)
式中:M、K分别为体系的质量矩阵和刚度矩阵;α、β为阻尼系数。
根据振型正交条件,α、β与振型阻尼比之间满足以下关系:
(5)
式中:ξk为阻尼比;ωk为固有圆频率;fk为固有频率。
模型计算采用收敛性较好的Newmark直接积分法,其基本假定如下:
t+Δtu′=tu′+[(1-δ)tu″+δt+Δtu″]Δt
(7)
式中:α、δ为Newmark计算参数,α=0.5、δ=0.25时始终稳定;Δt为积分时间间距。
3 超大断面双层隧道动力响应分析
3.1 计算条件
由于大罗山隧道出口段地质条件复杂,围岩条件差(Ⅴ级),选取出口段50 m作为运营期研究对象。根据隧道实际施工进尺及锚杆布置间距,模型网格长度取为0.5 m,整个隧道三围模型尺寸为长74.5 m×宽50.0 m×高53.5 m。土层、衬砌及车道采用实体单元模拟,支护锚杆采用桁架单元模拟。围岩和支护结构参数见表1。

表1 围岩和支护结构参数
锚杆直径为0.025 m。根据抗压强度相等的原理,将I18工字钢拱架的弹性模量按式(8)折算到砼弹性模量中,便于模型计算与处理。
(8)
式中:E为折算后喷射砼弹性模量(MPa);E0为原砼弹性模量(MPa);Sg为钢拱架截面面积(m2);Eg为钢材的弹性模量(MPa);Sc为砼截面面积(m2)。
3.2 动力响应分析
t为0.5 s、1.0 s、1.5 s、2.0 s、2.5 s、3.0 s、5.0 s时隧道结构竖向位移峰值见图1~7。由图1~7可知:1) 在车辆前轴开始作用于隧道内车道时,车道竖向位移逐渐增大;中间车道竖向位移最大,逐渐向两边减小,相同位移区域呈圆环状;随着车辆载荷向前移动,车道竖向位移主要影响区域以整体圆环形式向前移动,位移主要影响区域为中间最大位移处前方、后方各17 m处。2) 隧道衬砌受到车辆载荷的影响产生位移响应,位移主要响应区域为圆形衬砌与车道衔接处,即隧道圆形衬砌左腰、右腰附近区域;拱顶虽然产生位移变化,但沉降量很小,最大值未超过2 mm。
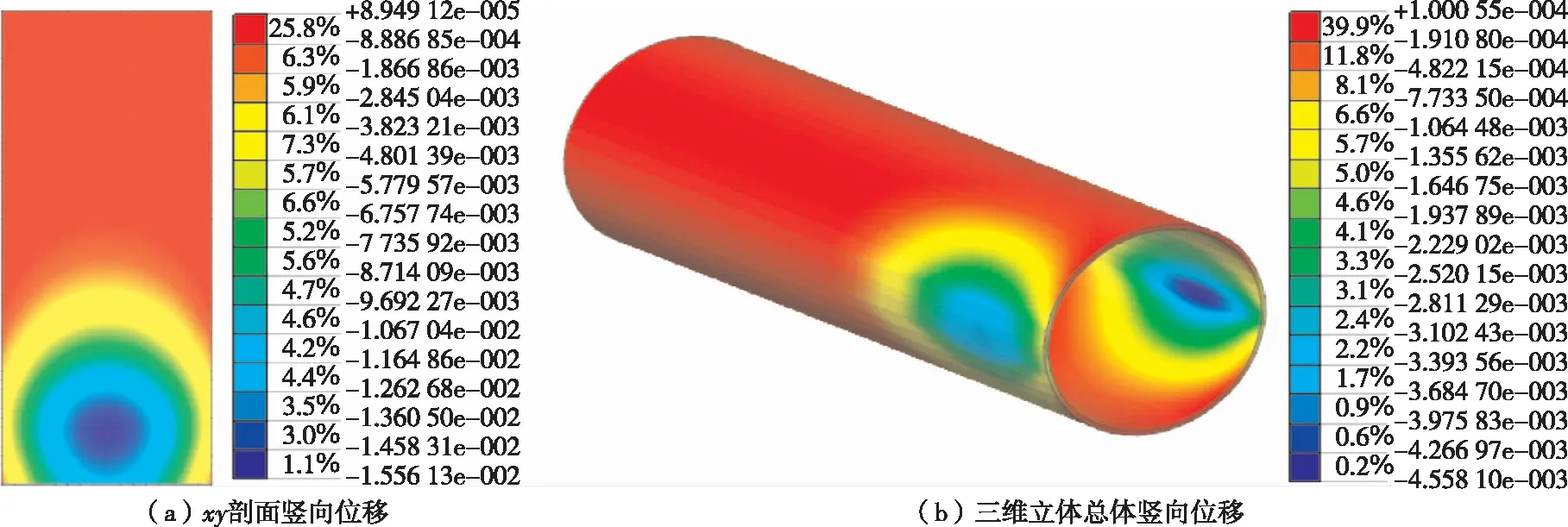
图1 t=0.5 s时隧道结构竖向位移峰值(单位:m)
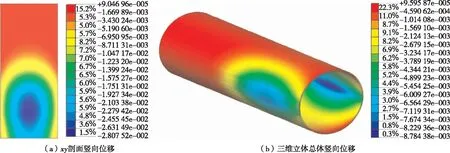
图2 t=1.0 s时隧道结构竖向位移峰值(单位:m)
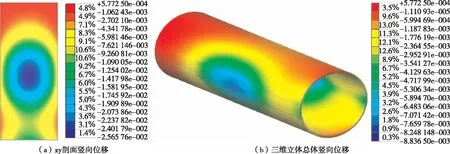
图3 t=1.5 s时隧道结构竖向位移峰值(单位:m)
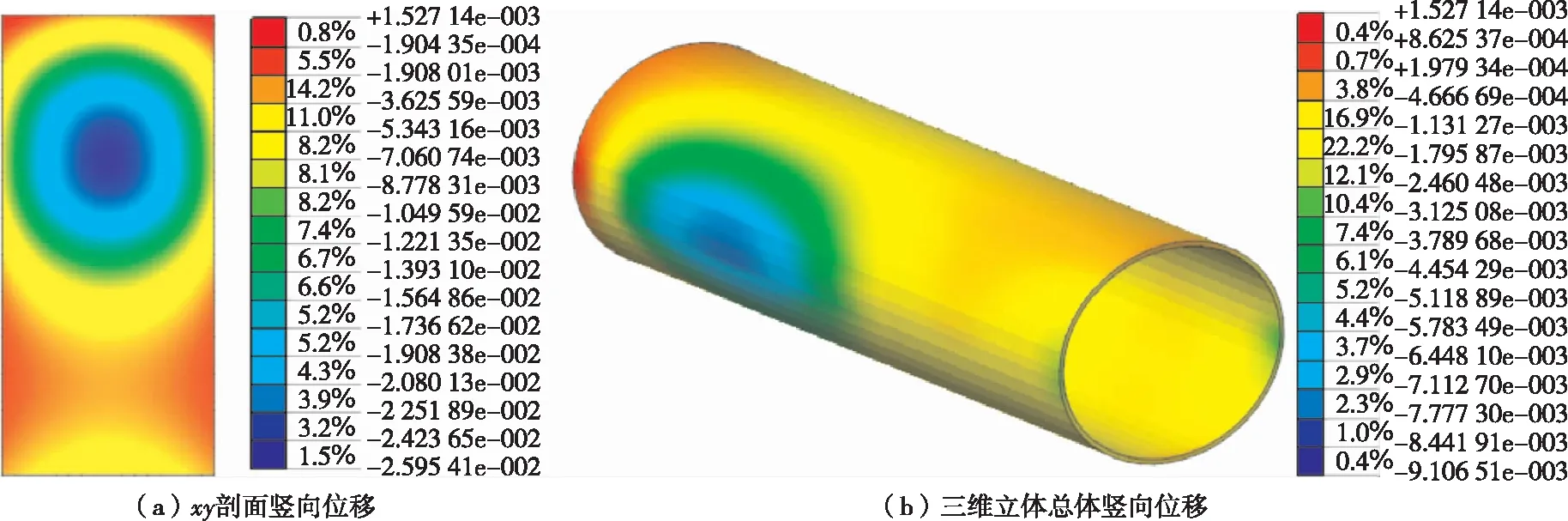
图4 t=2.0 s时隧道结构竖向位移峰值(单位:m)
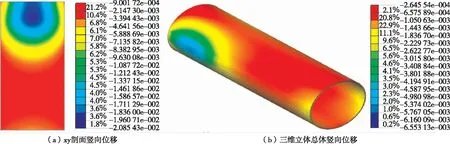
图5 t=2.5 s时隧道结构竖向位移峰值(单位:m)
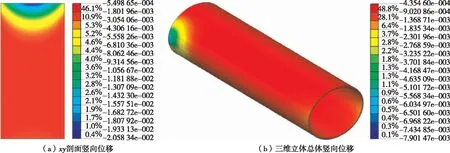
图6 t=3.0 s时隧道结构竖向位移峰值(单位:m)

图7 t=5.0 s时隧道结构竖向位移峰值(单位:m)
根据计算结果,位移在车道中轴线上达到最大值。考虑到车道底面是整个隧道结构中最薄弱处,选取车道底面中轴线上4个节点进行位移时程分析。4个节点分别为车道底面中轴线上起始点、中点、全过程峰值点、终点,分别用A、B、C、D表示,各点位移时程曲线见图8~11。由图8~11可知:1) 受到车辆荷载作用时,4个节点都向下产生沉降并逐渐增大,达到峰值后竖向位移逐渐减小,随着载荷作用周期结束而停止。荷载周期结束后,4个节点位移都不能回到原点,会产生位移积累,位移积累值将近1 mm。2) 各点未受到车辆载荷作用或作用周期结束时,加速度时程曲线产生上下波动,表明加速度在车道传递距离较长。A点加速度峰值大于B点峰值,B点加速度峰值大于C点峰值,D点加速度峰值在4个节点中最大,为0.009 8 m/s2。这是由于D点位于隧道出口段,加速度无法再向前传递。
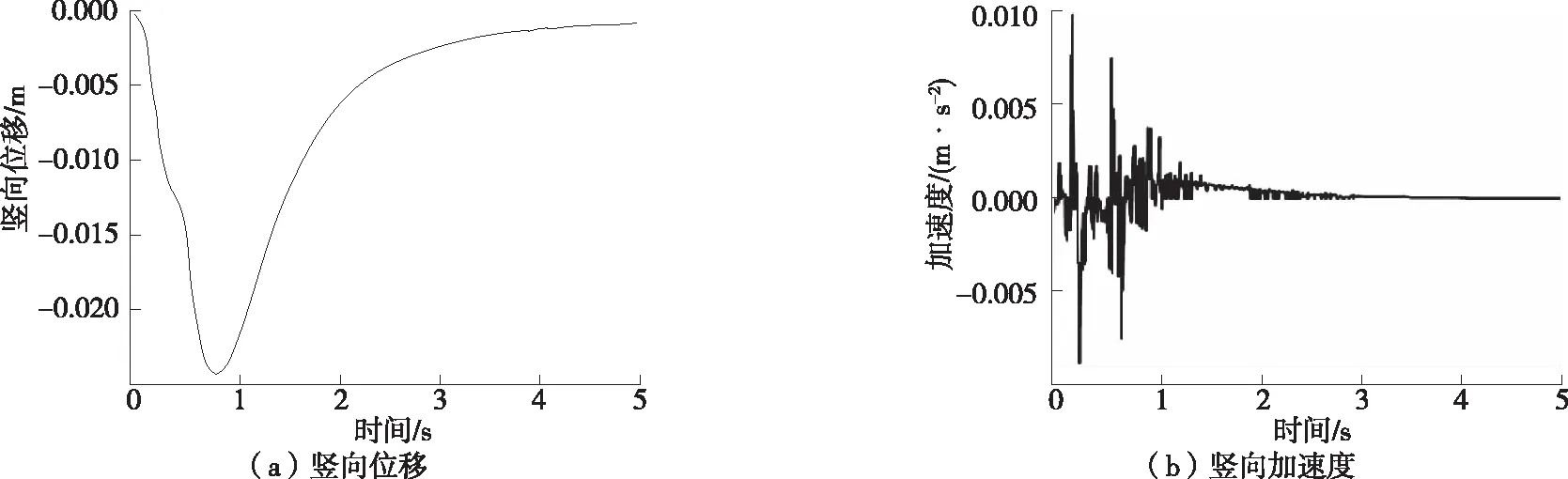
图8 A点位移时程曲线
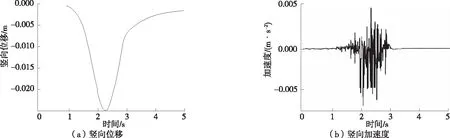
图10 C点位移时程曲线
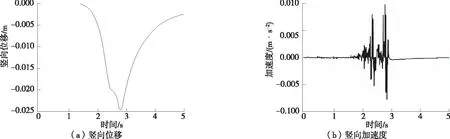
图11 D点位移时程曲线
4 结论
(1) 车辆荷载作用下,隧道结构产生的动力响应具有明显的三维性和时程性,三轴方向均产生位移响应,并随着车辆荷载的加载周期产生响应。
(2) 车道、衬砌和围岩中,车道位移变化最大,其次是衬砌,围岩位移变化最小,三者位移都在t=2 s时(距离隧道出口5 m处)达到最大值。车道中间区域沉降最大,衬砌则在与车道衔接处位移最明显。
(3) 在荷载作用周期结束后,隧道衬砌结构产生位移残余;随着隧道轴线方向距离的不断增加,车道加速度响应总体上不断衰减,仅在出口段加速度有所增加。
