公路高陡边坡施工稳定性动态监测研究
2022-08-09赵锡灿
赵锡灿
(云南省公路工程监理咨询有限公司, 云南 昆明 650021)
边坡稳定性不仅受结构和地质等内在因素的影响,还受降雨和载荷等外在因素的影响,边坡稳定性动态监测不易实现。针对高陡边坡的稳定性监测,王旭等利用三维激光扫描技术研究高陡边坡监测预警方法,根据位移情况进行风险等级分类,通过对高风险区域总位移变化的监测,实现高陡边坡稳定性监测;焦满岱等采用强度折减法进行高陡边坡稳定性分析,通过FLAC3D仿真软件构建边坡三维模型,实时分析模型坡面的稳定状态。虽然上述方法都能实现对高陡边坡稳定性的监测,但监测过程易受地域地质的影响,适用性和监测准确率还需进一步提高。该文开展公路高陡边坡施工稳定性动态监测研究,利用果蝇算法,设置若干监测点寻找边坡危险性最高的位置,通过合理布设传感器实现边坡稳定性动态监测。
1 工程概况
某沿河高陡边坡长152 m,坡向西倾,边坡角度为30°~46°,高度大于100 m。该边坡位于正断层和逆断层之间褶皱轴附近,地质岩体易破碎,浅表易风化。边坡基本由砂岩地层构成,岩体主要为板岩和薄砂岩,偶有紫红色砂岩,由于经年累月的风化,浅岩层呈外倾趋势。边坡中最重要的结构面为310°~340°∠10°~30°、5°~30°∠6°~24°、120°~180°∠6°~24°、100°~138°∠8°~27°。
2 高陡边坡动态监测
2.1 果蝇算法
果蝇算法是一种启发式算法,根据果蝇觅食的行为进行模拟,针对目标函数展开最优解寻找。该算法具有较强的收敛能力、精简的算法结构、较高的运行效果、能展开全局搜索等优势。果蝇觅食过程见图1。果蝇算法步骤如下:
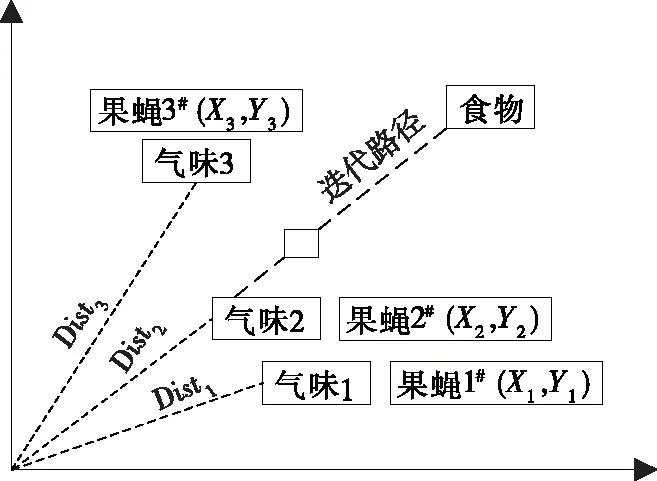
图1 果蝇觅食过程示意图
(1) 初始化果蝇种群。确定种群大小、果蝇搜索步长和迭代次数最大值,设坐标(Xaxis,Yaxis)为初始位置。
(2) 任意飞行。在(Xaxis,Yaxis)处设定各果蝇的飞行方向及位置信息,果蝇在允许范围内进行搜索,位置计算公式为:
(1)
(3) 目标函数中存在部分不能正确表示果蝇位置的坐标,可通过计算距离函数的倒数,将其设定为味道浓度判定值,即:
(2)
式中:Disti为距离函数。
(4) 确定味道浓度值。利用判定值,根据式(3)获取味道浓度。味道浓度值与果蝇距离成正比。
Smelli=f(Si)
(3)
(5) 位置标记。选取最大浓度值作为第二次迭代的初始位置。迭代过程中,若最优值的当前状态优于全局状态,则采用当前最优值,即:
[BbestSmell,BbestIndex]=max(Smelli)
(4)
(5)
式中:BbestIndex为味道浓度最大值;BbestSmell为味道浓度当前最优值。
重复步骤2~5,通过反复迭代寻找最优解,直到满足所有条件时停止迭代,提取当前最优解为最终最优解。
2.2 基于果蝇算法确定危险滑动面
(1) 将果蝇算法参数初始化,假设监测点数量为Spop,监测点位于高陡边坡最危险位置(X0,Y0,Z0),Mgen表示最大迭代步数,监测点数量≥传感器数量。
(2) 设定各监测点滑动方向和相邻之间的间距,利用递减搜索步长获取更新位置(Xi,Yi,Zi)。假设稳定系数最低的滑动面为各监测点当前位置,以当前各位置为界限将滑动体划分成单元体,滑动体受力状况见图2。滑动体从一个监测点到相邻监测点之间产生的抗滑力矢量和按式(6)计算,从一个监测点到相邻监测点之间产生的上下滑力矢量和按式(8)计算,稳定系数按式(9)计算。
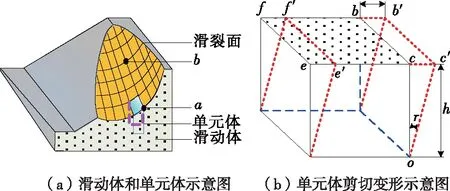
图2 滑动体受力三维立体图
(6)
式中:i=1,2,…,Spop;φ、c和δ分别为滑动面、土质的内摩擦角、内聚力和位移夹角;di-1,i、ni-1,i分别为位移方向和位移法向量,di-1,i按式(7)计算;m为高陡边坡比例系数;ω为位移方向和法向量之间的角度。
di-1,i=(Xi-Xi-1,Yi-Yi-1,Zi-Zi-1)
(7)
Ri-1,i=|Ri-1,i|cosv
(8)
式中:Ri-1,i表示合外力。
(9)
(3) 根据稳定系数,通过式(10)获取目标判定函数。此时所有监测点均处于最小稳定系数值的位置,高陡边坡危险系数最高,保留当前所有危险位置和稳定系数,表达式见式(11)。
[BbestSmell,BbestIndex]=min(Fs(i-1,i))
(10)
(11)
(4) 展开迭代寻找最优解,直至当前觅食代数小于最大觅食代数,且当前稳定系数小于上次稳定系数,通过式(11)获取最危险位置和最小稳定系数。
2.3 传感器布设
设置多个监测点,安装传感器进行危险滑动面监测。考虑到传感器需埋入土层中,埋设过多会破坏岩土结构,且会导致监测范围多次重合,影响监测结果,仅沿边坡滑动方向安装2个已封装的传感器,布设方案见图3。传感器垂直安装,底部固定牢固,安装完成后进行回填。
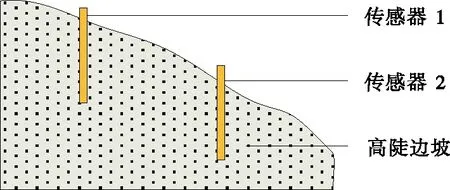
图3 传感器布设示意图
传感器布设位置计算公式为:
(12)
式中:s表示相邻两传感器之间的最大距离。
通过式(12)即可获取危险系数最高的监测点位置,即传感器安装位置,通过传感器实现公路高陡边坡施工稳定性动态监测。
3 试验验证
通过ANSYS软件进行高陡边坡施工稳定性模拟试验,在模拟滑动体上分别布置2个传感器。试验过程中开挖边坡下部,开挖后边坡见图4。
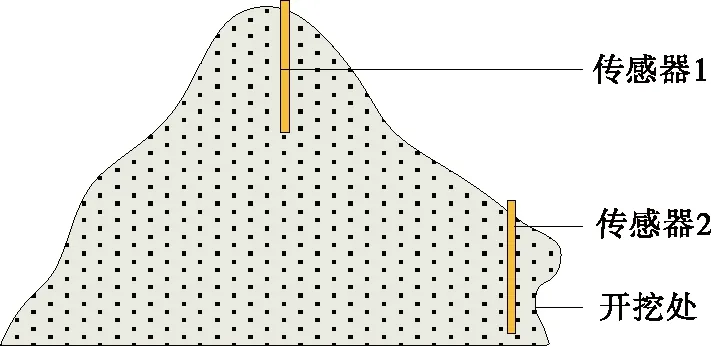
图4 开挖后高陡边坡示意图
监测13 min左右时,边坡发生轻微滑动,传感器监测结果见图5、图6。由图5、图6可知:在边坡发生轻微滑动时,1#传感器监测的上下部应力变化均不明显,变化值分别为4.18 με、3.79 με;2#传感器监测的上下部应力都发生强烈变化,变化值分别为38.76 με、24.31 με,且随着滑动幅度的加大,2#传感器监测的应力增大,上部和下部均在800 s附近发生骤变。滑动进行到1 768 s时,整个边坡发生失稳滑动,2个传感器的监测结果均发生剧烈变化。表明传感器能精准反映边坡变化情况,监测效果良好。
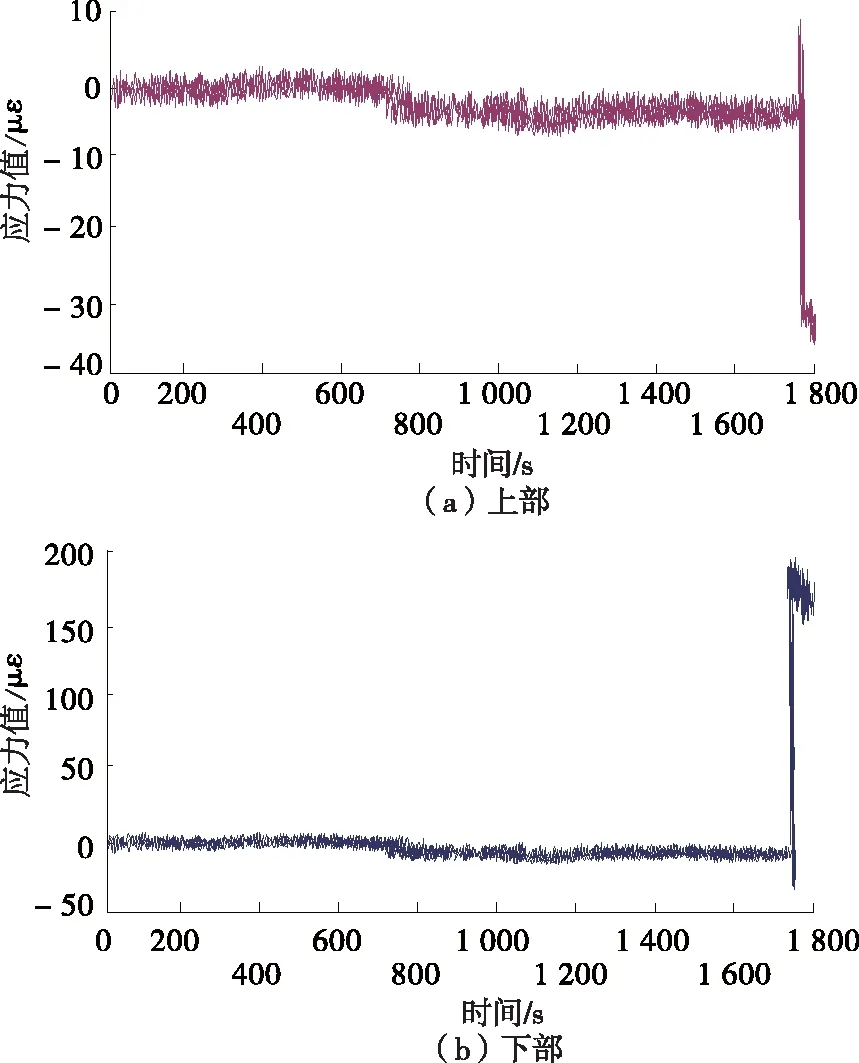
图5 1#传感器的监测结果

图6 2#传感器的监测结果
降雨是导致高陡边坡滑动的重要因素,相同时间下边坡因降雨产生的位移见图7。由图7可知:随着时间的推移,无降雨情况下边坡位移始终控制在0.2 cm以内,稳定性良好;降雨条件下边坡稳定性发生变化,随着时间的增加,位移变化逐渐加大,表明降雨对高陡边坡施工稳定性的影响较大。

图7 降雨对边坡稳定性的影响
不同降雨强度下传感器监测的边坡位移见表1。由表1可知:随着降雨强度的增大,边坡位移缓慢增大,降雨强度达到2.0 mm/min时,位移发生较大变化,且位移持续加大。表明采用文中方法在强降雨情况下能实现边坡稳定性动态监测。

表1 不同降雨强度下边坡位移
模拟降雨累积导致岩体裂隙水增多的现象。由于岩体中已有水压,边坡面上法向应力减小,降低了岩体的抗剪强度,严重影响边坡的稳定性。采用文中方法对边坡最大不平衡力进行监测,结果见图8。由图8可知:在边坡岩体渗流的作用下,岩体内聚力、强度及摩擦角降低,最大不平衡力随着渗流的变化发生巨大变化,边坡岩体产生变形,边坡稳定性降低。
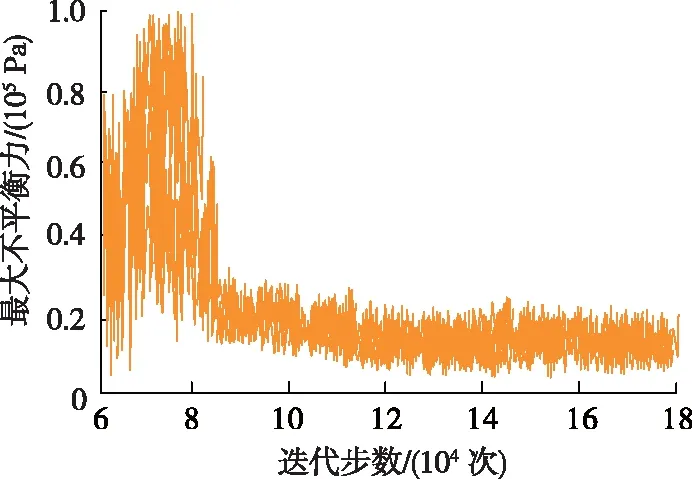
图8 边坡不平衡力变化趋势
分别采用文中方法、文献[7]中基于三维激光扫描的高陡边坡监测方法、文献[8]中基于强度折减法的高陡边坡稳定性分析方法进行监测效果对比,结果见图9。
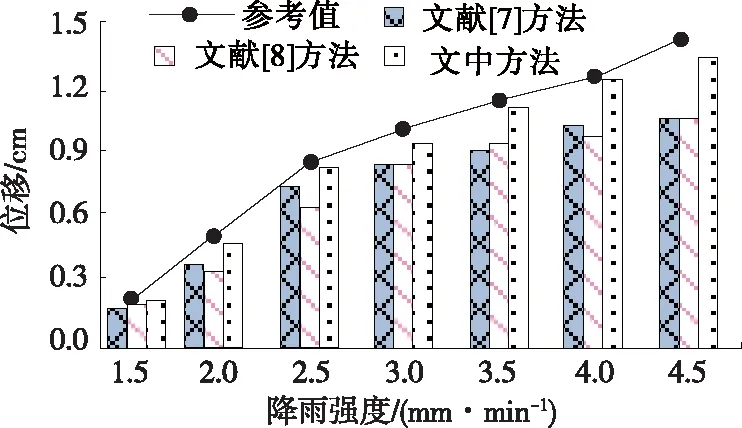
图9 不同方案监测效果对比
由图9可知:在相同条件下,以参考值为基准,文中方法监测结果的平均正确率为97.84%,比文献[7]中方法和文献[8]中方法分别高7.63%、9.12%,表明该方法具有较强的高陡边坡施工稳定性动态监测能力和适用性。
4 结语
利用果蝇算法确定的高陡边坡危险滑动面在高陡边坡中布设传感器,通过传感器对边坡施工稳定性进行动态监测,模拟试验结果表明该方法具有较强的高陡边坡施工稳定性动态监测能力和适用性。后续研究中,将进一步加强稳定性预警和响应研究,为公路高陡边坡施工提供更全面的保障。
