基于LCL滤波器的交流恒功率负载优化控制研究

刘欣博，刘 帆，施俊甫

（北方工业大学，北京 100144）

0 引言

电力系统中存在着大量电动机、变换器负载，这些负载一般通过闭环控制的变流器接入母线，当输入电压有效值变化时，输入电流有效值也会相应调整，消耗的有功功率不受输入电压变化的影响［1-2］，具有负阻抗特性［3-7］，会像正反馈一样放大扰动信号，对系统稳定性产生不利影响。例如，当系统电压出现大幅度突变时，这些闭环控制电动机、变换器负载可能造成母线电压振荡甚至崩溃，严重影响电力系统的正常运行［8］。

综上所述，对电力系统稳定性造成严重影响的实际上是闭环控制的电动机、变换器等实际物理装置。但是在对电力系统进行稳定性分析时，由于闭环控制的电动机、变换器等实际物理装置的结构、原理、控制策略非常复杂，需要对它们进行建模，一般以交流恒功率负载模型来代替实际物理装置。基于准确、简单的交流恒功率负载模型，可以对含闭环控制的电动机和变换器的电力系统进行动态性能和控制策略的优化分析。

目前对恒功率负载模型的研究主要集中在直流系统。文献［9］提出一种应用于源端DC/DC 转换器的复合控制器，研究恒功率负载对母线电压稳定性的影响。文献［10］提出一种适用于恒功率负载过压保护情况下的新型下垂控制，可以控制微电网每个电源电压的上限，并实现负载电压调节。文献［11］为了解决恒功率负载引起的电压不平衡问题，设计了特殊的前馈去耦网络，简化了控制系统，提高了系统的快速性和抗扰性。文献［12］将混合模型预测控制应用于恒功率负载闭环控制，以调节变换器的电压，但并未考虑模型的准确性。文献［13］提出一种单电感双输出DC/DC转换器结构，开环实现恒功率负载的控制，但是其控制方法的可靠性还有待考量。文献［14］将环路消除技术应用在不控AC/DC整流器上，以实现自适应稳定，但是恒功率负载的等效过于理想化。文献［15］考虑恒功率负载在无线电传输技术中的应用，提出单个转换器的次级侧控制策略，使直流侧恒功率负载电压恒定。

交流恒功率负载的负阻抗特性会使系统不稳定，其建模方法对于电力系统性能分析和稳定控制至关重要。传统交流恒功率负载模型的主电路由PWM（脉冲宽度调制）整流器连接电阻构成，结构非常简单，通过PWM整流器闭环控制实现负载功率可控。绝大部分交流恒功率负载模型应用最简单的双闭环PI（比例积分）控制，当调节速度较快时超调比较大，能够模拟应用PI 控制的电动机和变换器负载动态特性。文献［16］研究有源整流器连接的恒功率负载提供无功功率的潜力，以及有源整流器引入无功电流控制对系统总体电压稳定性的影响。文献［17-18］使用DQ 转换方法控制PWM整流器，推导出适用于稳定性分析的恒定功率负载的AC/DC电力系统数学模型，但是其控制效果并没有优化。近年来，随着大功率电动机动态性能的要求越来越高，MPC（模型预测控制）也广泛应用于电机调速，与传统PI控制相比，MPC方法调节速度快，超调小，鲁棒性强。传统PI 控制的交流恒功率负载模型很难准确体现应用MPC的电动机负载的动态性能［19］。另一方面，PWM整流器的高频开关动作会给电源带来严重的谐波污染［3］，为了提高电能质量，降低电流谐波，实际电力系统中电动机、变换器负载的输入端通常连接低通滤波器。LCL 型滤波器具有较好的高频段衰减特性和低频增益特性，电路结构简单，在相同滤波效果的情况下可以显著降低电感值，因而应用最为广泛［20］。

本文结合传统PI控制和MPC的优势，提出一种外环应用PI控制、内环应用MPC的新型交流恒功率负载模型，主电路由交流侧带LCL 滤波器的PWM整流电路与电阻共同构成，LCL滤波器根据电感总量、电容和谐振频率进行设计。

1 交流恒功率负载模型

1.1 交流恒功率负载原理

交流恒功率负载模型的主电路包括交流侧LCL滤波器、PWM整流器和阻性负载，如图1所示。首先建立PWM整流器在静止abc坐标系的开关函数模型，通过Park坐标变换将abc坐标系的非线性模型转化到dq旋转坐标系；接着应用MPC策略设计电流内环，包括建立预测模型和评价函数两个步骤，通过最小化评价函数来确定最优电压矢量，从而控制开关管的导通和关断，在电流内环的基础上确定电压外环PI 调节器参数。图1中：Va、Vb、Vc为交流母线三相电压；Ia、Ib、Ic为交流三相电流；θ为电网电压相位；Cdc为直流侧稳压电容；id（k）和iq（k）为dq轴的预测电流；ω为电网角频率；ωLid和ωLiq为电感在dq轴的耦合分量；Vd和Vq为交流三相电压经Park坐标变换后得到的dq轴电压分量实际值；Ud和Uq为最优电压矢量；id和iq分别为交流侧滤波电感电流经Park变换后得的dq轴电流实际值；idref和iqref为dq轴电流给定值；Vdc和Vqc为直流侧dq轴电压实际采样值；Vdcref和Vqcref为直流侧dq轴电压给定值。

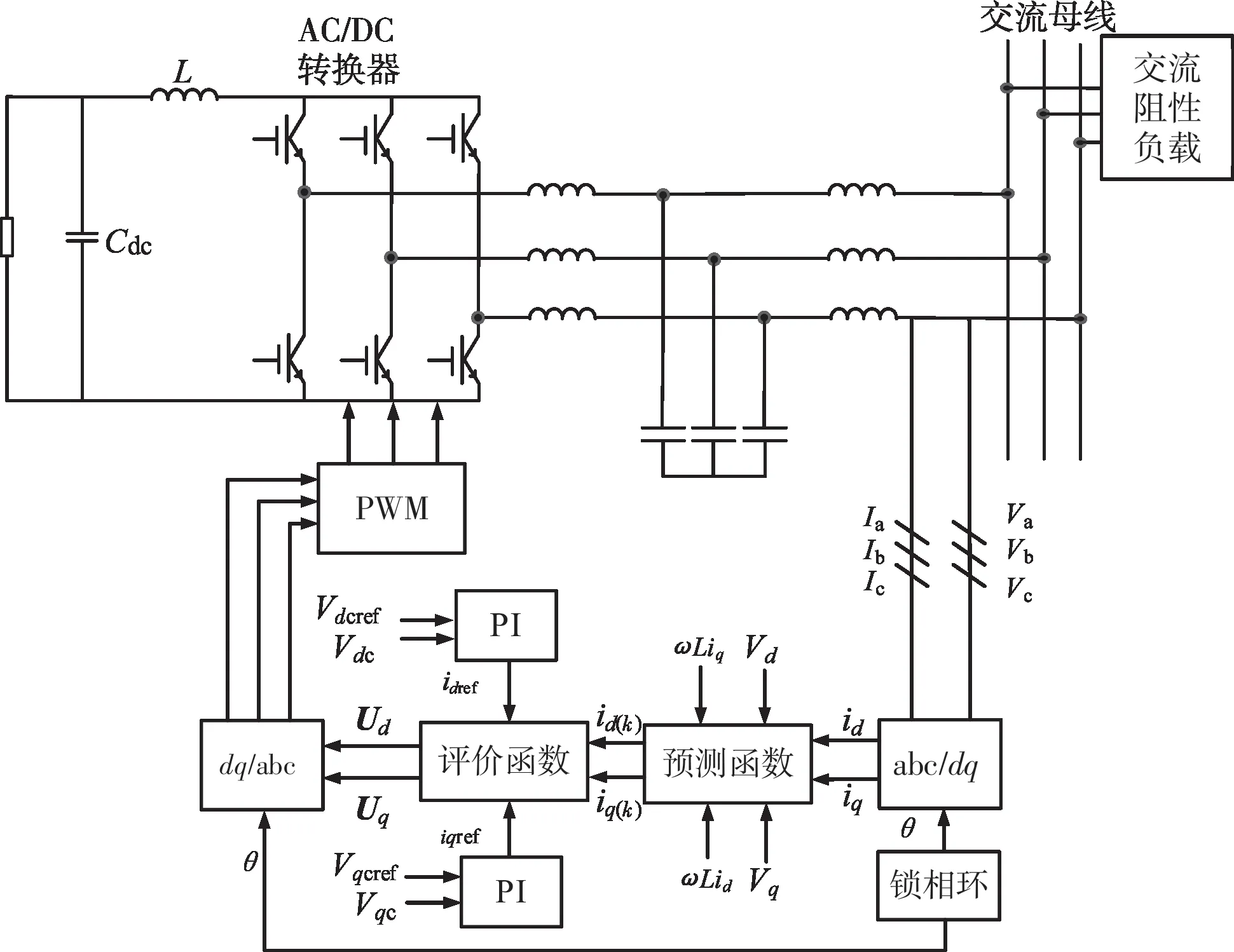
图1 交流恒功率负载优化控制系统原理

PWM整流器应用直流母线电压外环、交流侧滤波电感电流内环的双闭环控制，该控制策略可维持直流母线电压恒定，为阻性负载提供恒定的直流电压。首先，电压外环将Vdc与Vdcref比较，经过PI调节器后得到有功电流给定值idref。由于整流器工作在单位功率因数条件下，无功电流给定值iqref=0。将三相交流电流实际值通过abc/dq坐标变换，即得到有功电流实际值id和无功电流实际值iq。同理，将三相交流电压经过abc/dq坐标变换，分别得到dq轴分量Vd和Vq，以及电感的耦合分量ωLid和ωLiq。将Vd、Vq、ωLid、ωLiq输入预测函数模型，得到每个电压矢量对应的预测电流id（k）和iq（k），将预测电流代入评价函数，评价函数最小值所对应的电压矢量即为最优电压矢量Ud和Uq，进行dq/abc 反变换，产生PWM 整流器驱动信号，控制开关管的导通和关断。

1.2 PWM整流器主电路等效模型

三相PWM整流器拓扑如图2所示，其中：vdc为直流母线电压；N 为直流母线参考点；RL为负载电阻；i（jj=a，b，c）为三相电流；e（jj=a，b，c）为三相母线电压；eL为直流电动势；R为交流母线等效电阻；L为交流侧滤波电感。当直流电动势eL=0时，直流侧为纯电阻负载，建立采用开关函数描述的PWM整流器主电路数学模型。

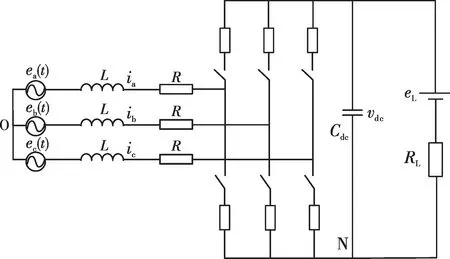
图2 三相PWM整流器拓扑

对PWM 整流器在abc 静止坐标系进行建模，首先定义开关函数sj为：

再根据基尔霍夫电压定律［21］建立三相回路方程为：

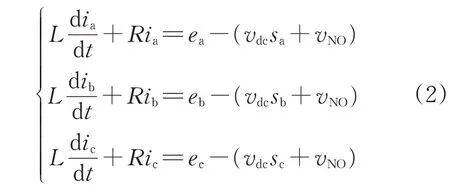
式中：vNO为N点与地之间的电压。

考虑交流系统为三相电压、电流对称系统，满足以下关系：

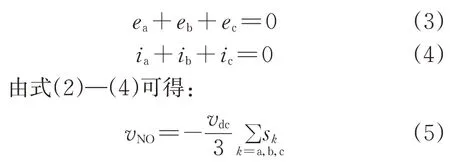
对直流侧电容及负载节点应用基尔霍夫电流定律［21］可得：

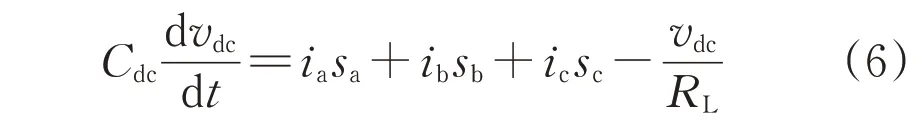
上述PWM 整流器主电路数学模型是基于abc静止坐标系建立的，包含三相时变交流量，较为复杂，不利于进行下一步分析控制，需通过坐标变换，将abc坐标系下的三相交流量转化为以电网基波频率旋转的dq坐标系下的直流量，如图3所示。

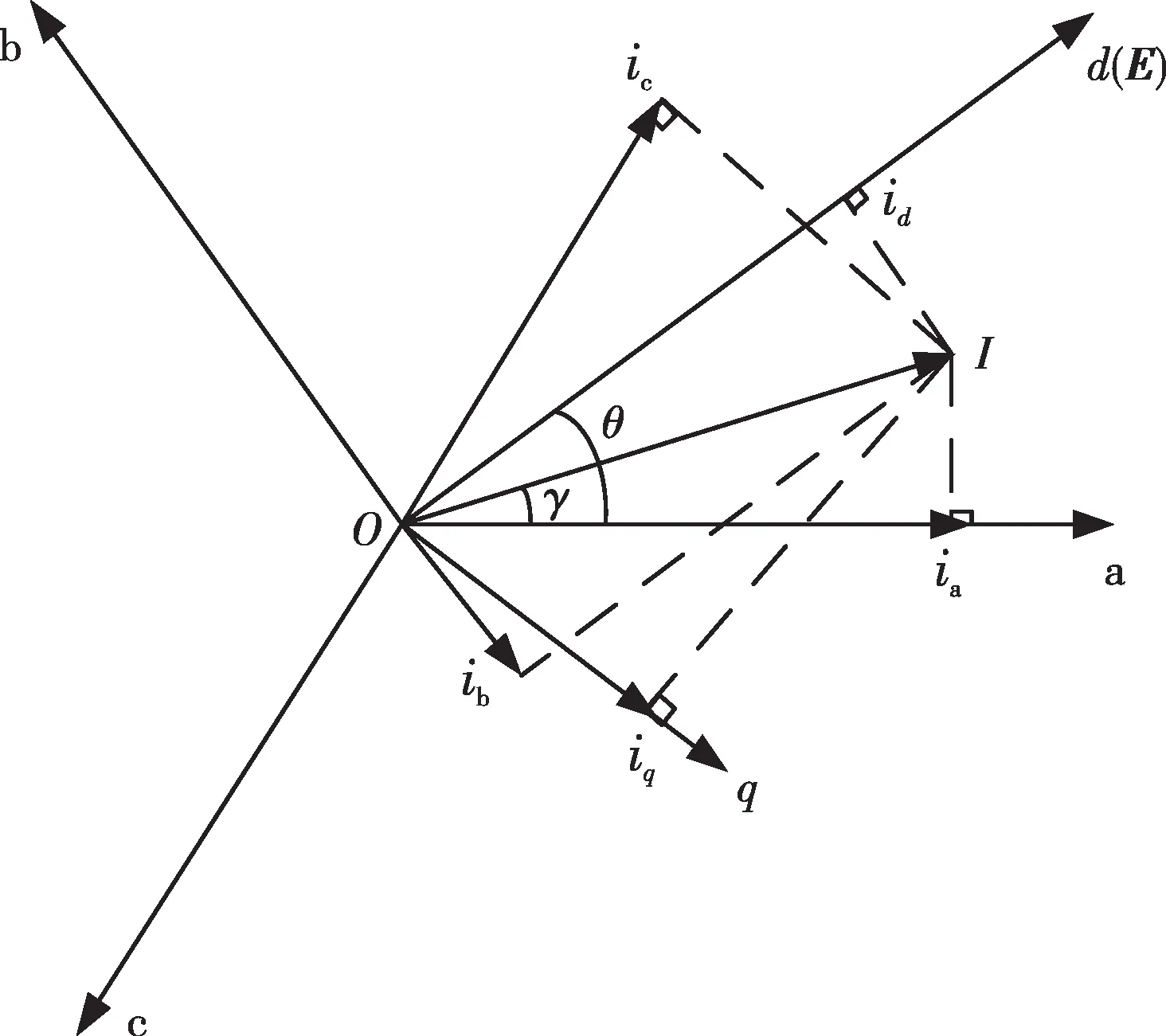
图3 dq旋转坐标系和abc坐标系

三相静止abc 坐标系到dq同步旋转坐标系的变换矩阵为：

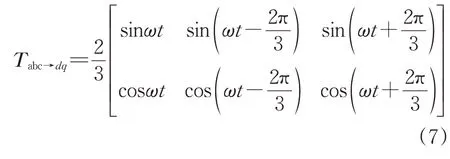
将式（7）代入式（2）并化简，得两相dq同步旋转坐标系中PWM整流器的数学模型为：

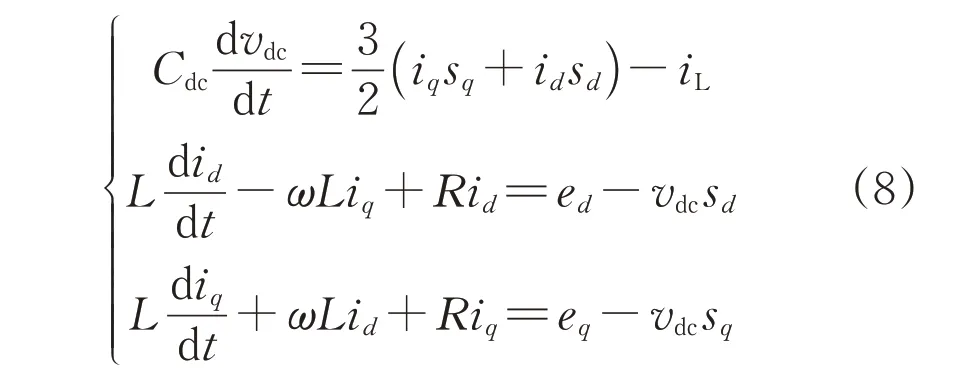
式中：iL为负载电流；ed和eq为电网电动势e的dq轴分量。

在dq旋转坐标系中，PWM 整流器主电路可以等效为一个两端口输入、单端口输出的三端口网络，且符合功率守恒原理，如图4所示，其中idc为直流侧电流。

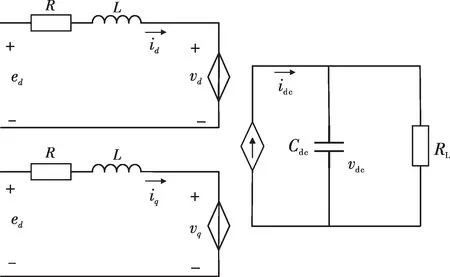
图4 PWM整流器主电路等效模型

1.3 LCL滤波器设计

电力系统中，PWM 整流器的开关频率较高，因此高次谐波比较多，交流侧电能质量不理想。为了抑制谐波，提高电能质量，需在交流侧加入滤波器［22］。滤波器原理如图5 所示，其中L1为桥臂侧电感，L2为网侧电感，Cf为交流侧电容。滤波器输入电压U（s）与输出电流I2（s）的传递函数为

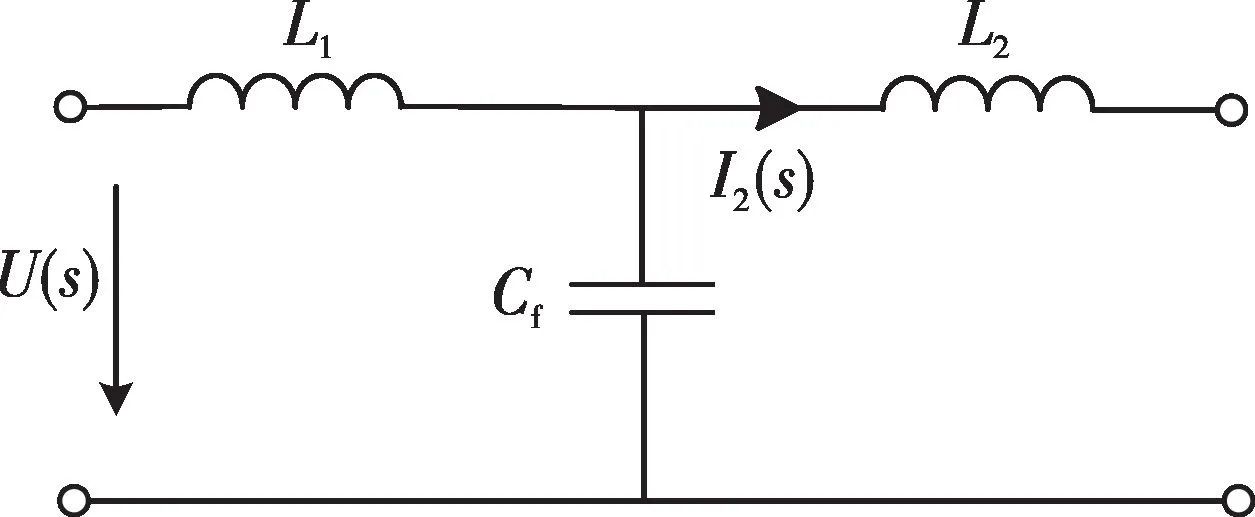
图5 LCL滤波器原理

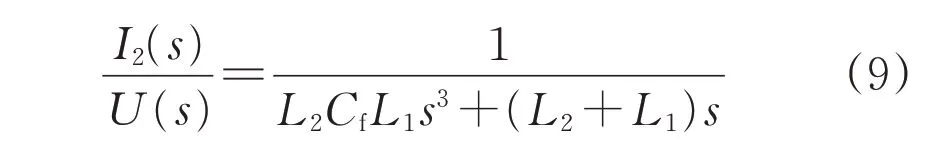
式中：s为拉普拉斯算子。

图6 为LCL 滤波器的伯德图。和L 型滤波器相比，LCL 滤波器在低频段的增益基本一致，但在高频段的衰减程度明显低于L 型滤波器，且滤波器在固定角频率ωres处存在谐振，谐振角频率的计算公式为：

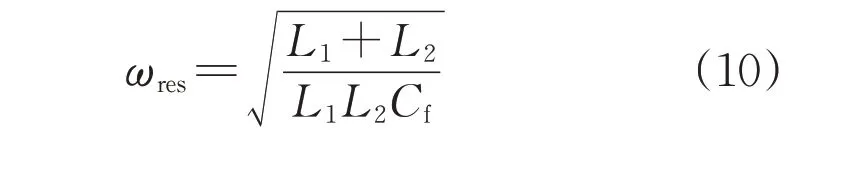
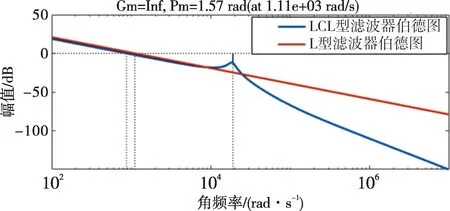
图6 滤波器伯德图

LCL 滤波器的参数设计有4 个限制条件，即总电感量（L1+L2）的上限设计、滤波电容Cf的上限设计、谐振频率fres的上下限设计、LCL 滤波器电感参数设计。

1.3.1 总电感量（L1+L2）的上限设计

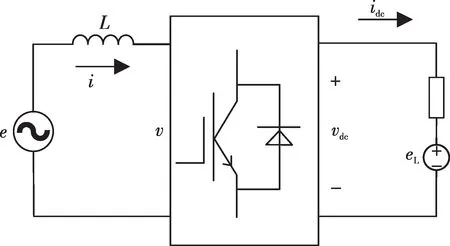
图7 PWM整流器简化模型

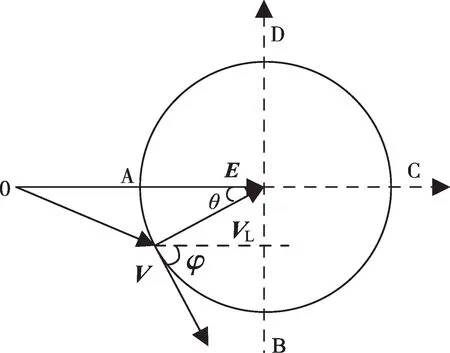
图8 稳态运行时PWM整流器电网侧矢量图

选择适当的电感和直流电压值，即可控制PWM整流器运行在矢量圆周的任意一点，在电感L取值一定的情况下，不同电流对应不同的圆周。当PWM整流器在C点工作时，电感设计的上限值最小；而当PWM 整流器运行于A 点时，电感设计的上限值最大。设计时考虑最严重的情况，即PWM整流器工作在C点的情况，可得滤波器总电感取值的上限值范围为：

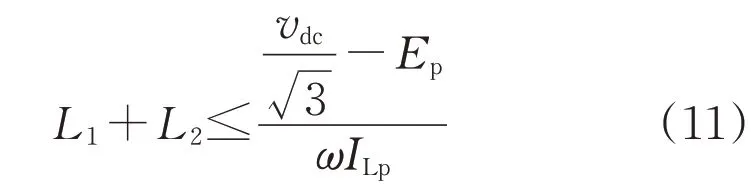
式中：Ep为网侧电压峰值；ILp为电感电流峰值。

1.3.2 滤波电容Cf的上限设计

在PWM 整流器中，LCL 滤波器的滤波电容值越大，滤除高频电流的能力就越强，产生的无功功率也越多，从而降低了PWM整流器的功率变换能力。因此设计LCL 滤波器时，需要限制电容产生的无功功率，即要求电容的无功功率不超过系统额定功率的5%，即：

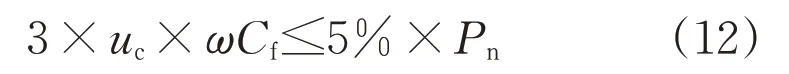
式中：uc为电容电压；Pn为PWM 整流器的额定功率。

当滤波电感的压降较小时，电容电压uc可近似为电网电压un，满足uc=un，因此可将式（12）转化为：

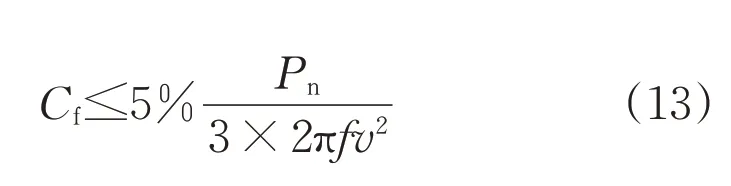
式中：f为电网频率。

1.3.3 谐振频率fres的上下限设计

关于读者是否关注了图书馆的微信公众号：调查结果为约70%的读者已关注，约29%的读者没有关注。已关注的读者中约有60%对该微信公众号的功能和信息表示满意；约40%的读者表示不满意。

不同功率PWM 整流器的开关频率也不相同，设计LCL滤波器的谐振频率fres时，一方面需要考虑滤波器应充分滤除开关频率有关的谐波，另一方面应使控制系统具有足够的控制带宽和稳定裕度。通常可根据开关频率范围确定LCL 滤波器谐振频率fres的上下限设计范围，即：

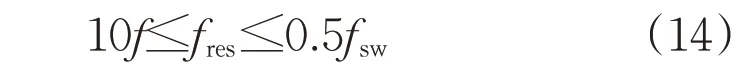
式中：fsw为PWM整流器的开关频率。

1.3.4 LCL滤波器电感参数设计

LCL 滤波器电感包括桥臂侧电感L1和网侧电感L2。桥臂电流纹波过大不仅增大滤波元件损耗，还使功率开关管承受较高的开关应力，影响PWM整流器的控制。一般将LCL 滤波器的桥臂侧电感L1取得大一些，而网侧电感L2取得小一些，满足：

式中：γ为网侧电感与桥臂侧电感的比例系数，一般取γ≤0.5。

对于LCL滤波器设计而言，谐振频率ωres的表达式为：

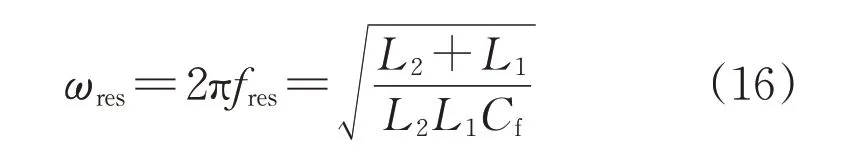
将式（15）带入式（16），可得：

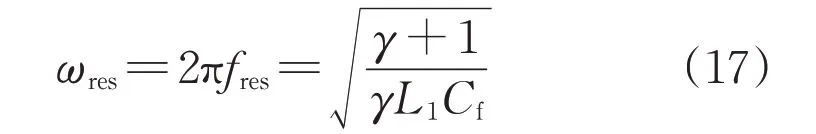
则桥臂侧电感L1需满足：

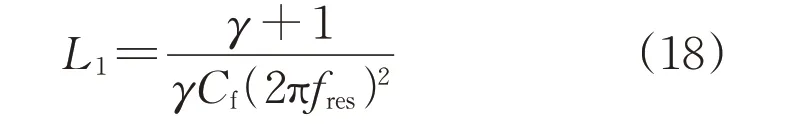
由于LCL 滤波器的网侧电感L2较小，比例系数γ可取0.2。

2 交流恒功率负载的控制系统设计

对于三相交流对称系统，若只考虑交流基波分量，则稳态时dq坐标系的dq轴分量均为直流量；另一方面，当dq旋转坐标系的d轴与电网电动势矢量E重合时，d轴为有功分量参考轴，q轴为无功分量参考轴，有利于PWM整流器分别控制网侧有功、无功分量（本文中无功分量为0）。

2.1 电流内环PI控制器设计

将dq坐标系以电网电动势E定向d轴，则PWM整流器dq旋转坐标系的模型可简化为：

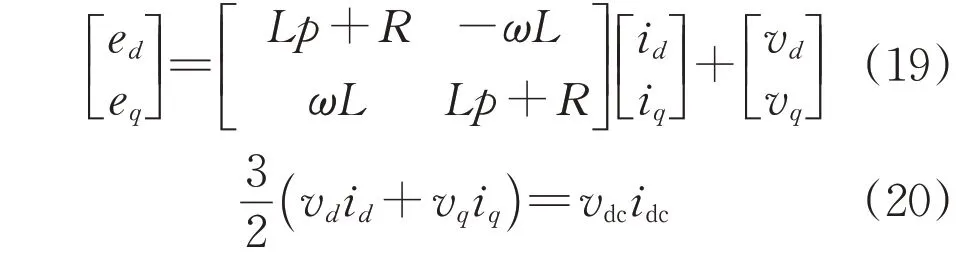
式中：p为微分算子。

在同步旋转坐标系dq中，d轴以电网电动势矢量E定向，dq轴变量相互耦合，因此采用前馈解耦控制，vd和vq的控制方程为：

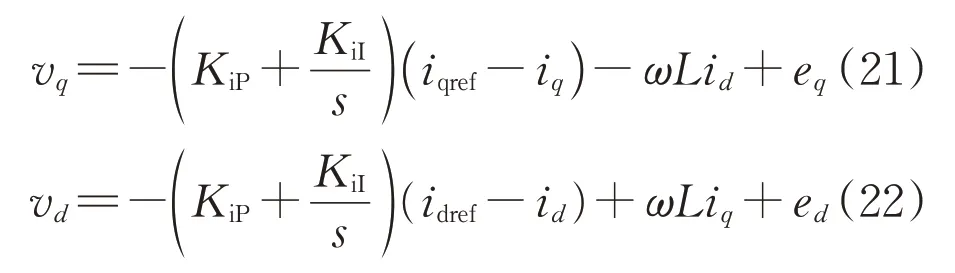
式中：KiP和KiI分别为电流内环的比例系数和积分系数。

将式（21）和（22）代入式（19），整理可得：

式（23）表明式（21）和（22）实现了解耦控制，控制框图如图9所示。

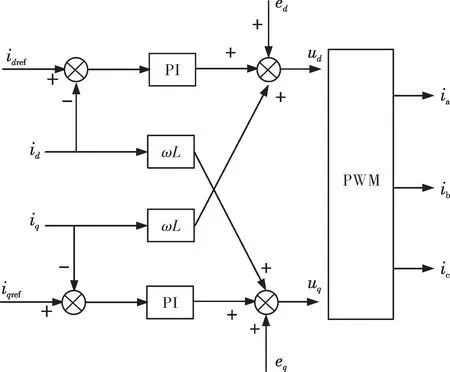
图9 电流内环解耦控制结构

本系统令d轴以电网电动势矢量E定向，因此以iq控制为例设计控制调节器，控制系统暂时不考虑eq的扰动，并将传递函数写成零极点形式，解耦后的iq电流内环控制框图如图10所示。

图10 id控制框图

图10中，Ts为电流内环采样周期，KPWM为桥路PWM 等效增益。按典型I 型系统设计，令τi=L/R即可以PI 调节器零点抵消电流控制对象传递函数极点。以此方法所得电流内环的开环传递函数为：

求解可得电流内环PI 控制参数KiP和KiI的计算公式为：

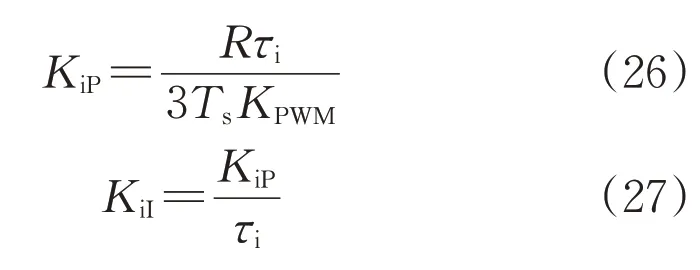
2.2 电流内环MPC设计

MPC 设计步骤包括建立预测模型和使评价函数最小化，从而选择最优的开关状态，对控制目标的性能进行优化。MPC的核心在于评价函数的设计，通过评价函数选择最优电压矢量，即分别计算8个电压矢量对应的评价函数值，选取评价函数最小值所对应的电压矢量作为最优电压矢量，控制PWM整流器开关管的导通和关断。

若忽略线路电阻R，同步旋转dq坐标系下PWM整流器模型方程满足：

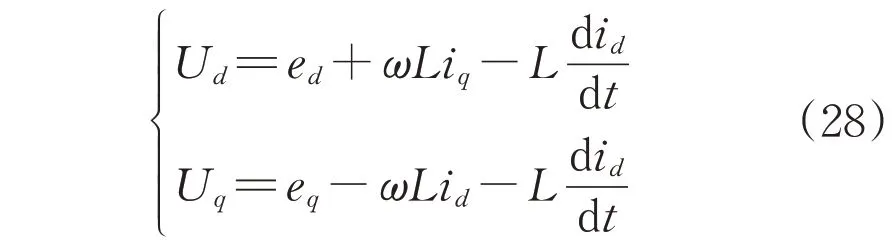
式中：ed=E，eq=0。

当开关频率足够高时，电感电流微分形式可近似为：

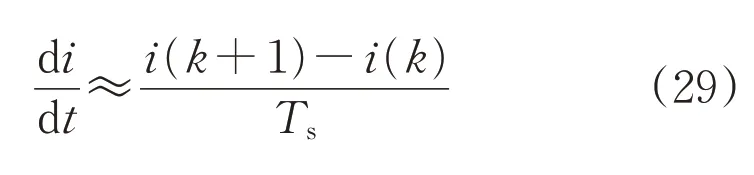
式中：（ik）为kTs时刻电流预测值。

将式（29）带入式（28），并将离散时间向前推导，可得：

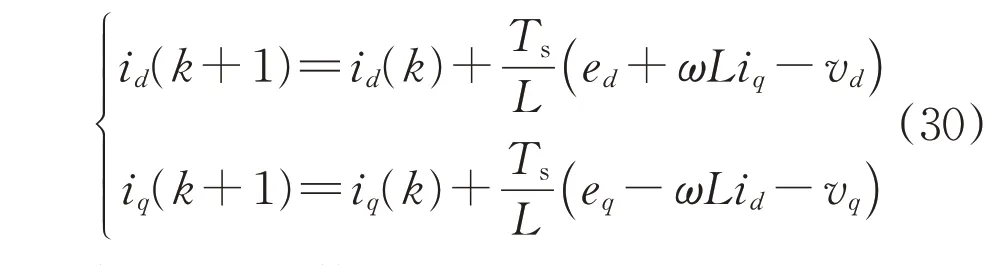
定义评价函数为：

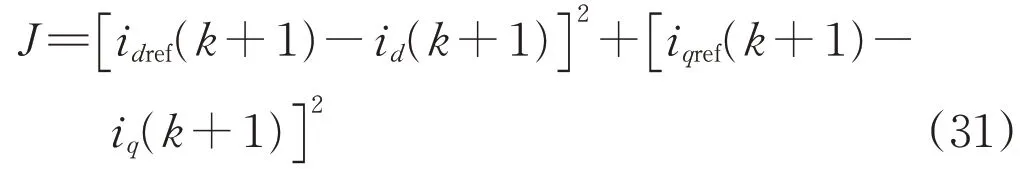
式中：idref（k+1）和iqref（k+1）为（k+1）Ts时刻dq轴的电流参考值，可由电压外环计算得到。由于d轴以电网电动势矢量E定向，iqref（k+1）=0。

在每个采样周期内，根据参考电流所处的工频半周，将8个开关状态对应的电流预测值分别代入式（31）滚动寻优，选取评价函数J最小时对应的电流预测值作为最优预测值，实现电流跟踪控制。依据评价函数式（30）和（31）选取最优电流矢量id、iq，再返回式（28）得到最优电流矢量对应的最优电压矢量ud和uq，经dq/abc 坐标反变换得到ua、ub、uc，从而控制PWM 整流器开关管的导通和关断。电流内环MPC算法流程如图11所示。

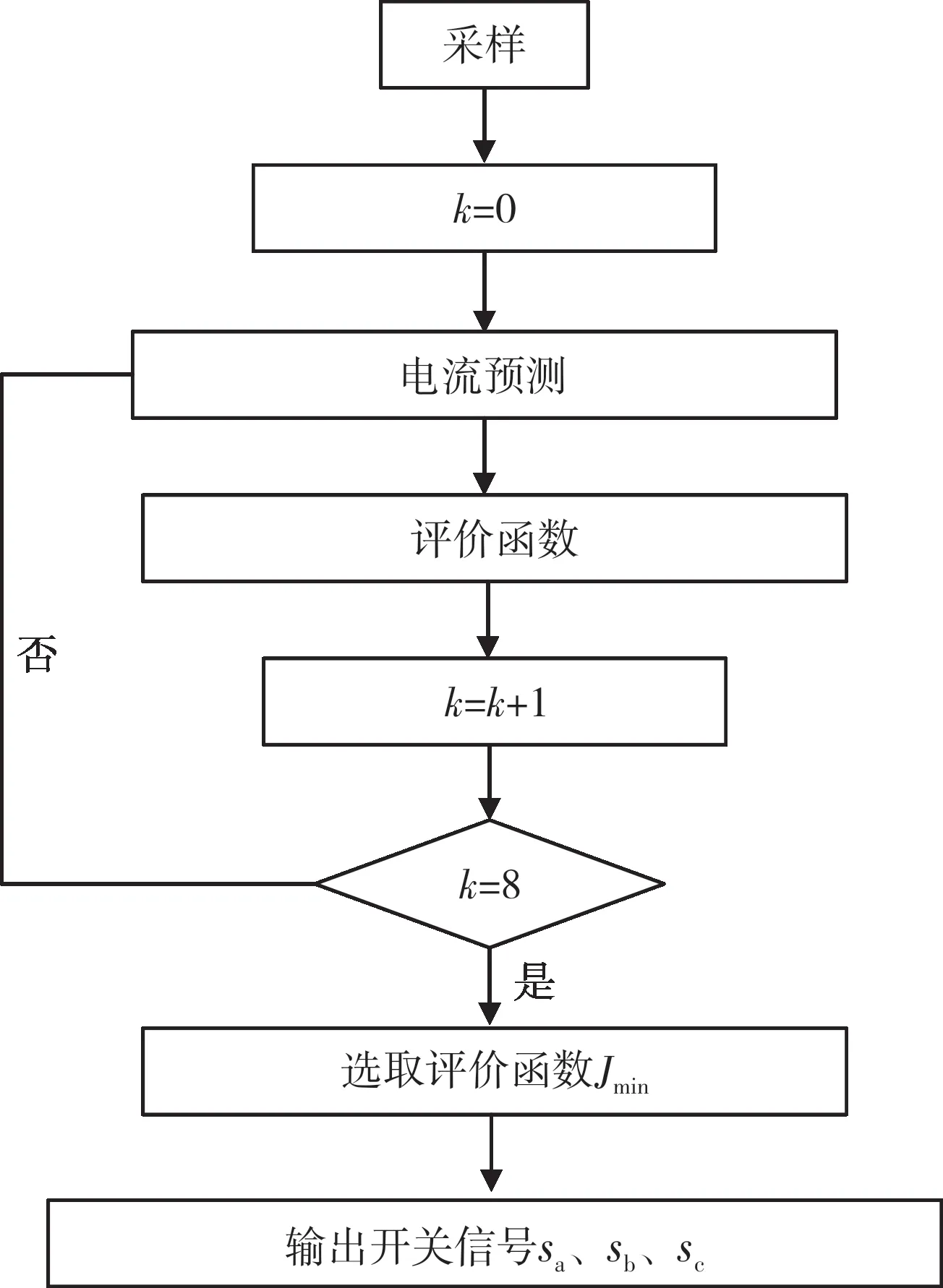
图11 电流内环模型预测算法流程

2.3 电压外环PI控制器设计

电压外环控制的目的是稳定直流侧电压vdc。网侧三相电压与三相电流分别为：

式中：Im为交流侧相电流幅值；Em为交流侧电网电压幅值。

变换器开关频率远高于电网基波频率，因此只考虑开关函数的低频分量，则有：

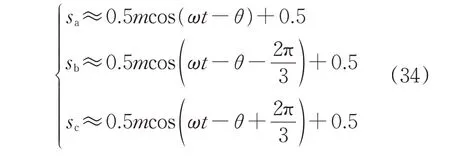
式中：m为PWM的调制比，m≤1。

此时直流侧电流可表示为：

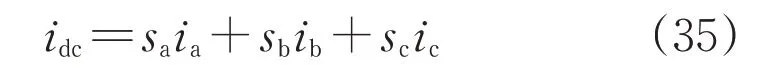
将式（33）、（34）代入式（35），化简可得：

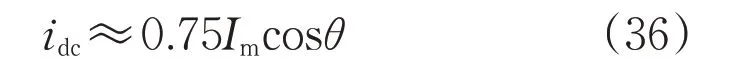
电压外环简化后的控制框图如图12所示。

图12 电压外环控制框图

图12中，Tv为电压外环PI调节器参数。为简化控制结构，将电压采样小惯性时间常数τv与电流内环等效时间常数3Ts合并，即Tev=τv+3Ts。考虑到电压外环的抗干扰性，将其设计成二阶系统，由图12可得开环传递函数为：

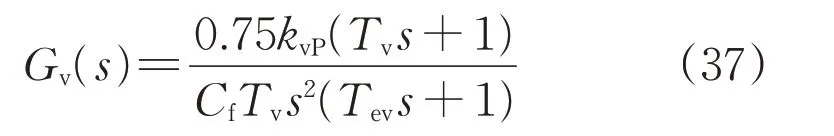
式中：KvP为电压环比例系数。

电压环中带宽hv满足：

可得到电压外环PI调节器控制方程为：

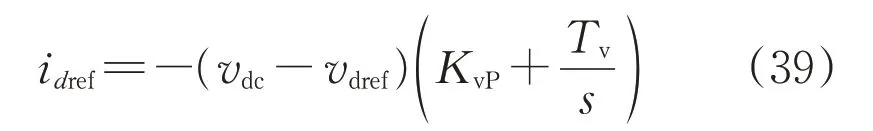
式中：vdref为直流侧电压给定值。

接着，由二阶系统控制器参数整定关系［23］可得：

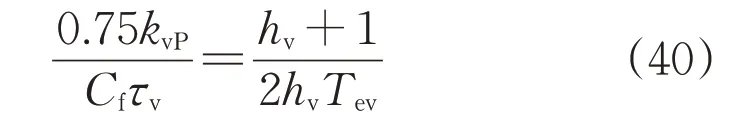
综合考虑电压外环的抗干扰能力及跟随性，取带宽hv=5，Tv=5Tev=5（τv+3Ts），代入式（40）可得：

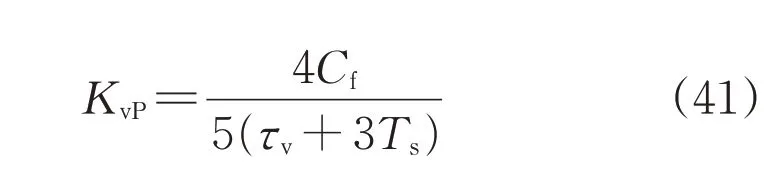
当 取τv=3Ts时，Tv=5Tev=5（τv+3Ts）=20Ts，为与KvP形式一致，令电压环积分系数KvI=Tv，即：

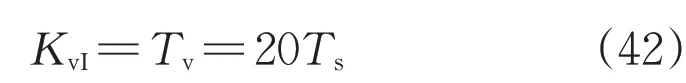
电压外环PI调节器输出电流给定值idref，作为电流内环的参考值。

3 仿真分析

应用MATLAB-Simulink 仿真软件进行仿真验证。为了验证本文设计的交流恒功率系统模型采用电压外环PI 控制、电流内环MPC，比电压、电流双PI 控制具有更强的鲁棒性和稳定性，搭建两种控制电路进行对比；为了验证交流侧具有较高的波形质量，搭建主电路为LCL 滤波器连接PWM整流器的等效电路。

3.1 恒功率负载主电路仿真模型搭建

图13 为交流恒功率负载的主电路模型，交流电网通过LCL 滤波器与PWM 整流器相连，电流经整流器由交流变为直流，直流侧负载由电阻等效且并联电容进行稳压，整个系统可以视为交流恒功率负载接在电网中。系统的初始环境为：交流系统母线的相电压有效值220 V、峰值311 V，电网频率50 Hz，交流恒功率负载的额定功率Pn为5 800 W，PWM 整流器开关频率fsw为20 kHz，直流电压vdc为800 V，峰值电压Ep为311 V，电感电流峰值ILp为16 A。t=1 s 时交流母线相电压峰值由311 V升至367 V，模拟系统大扰动条件。

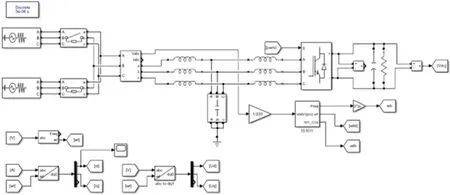
图13 交流恒功率负载主电路仿真模型

由式（11）计算得到总电感量?需满足L1+L2≤1.1×10-2H；将PWM整流器额定功率Pn以及电容电压uc的值带入式（13），可得滤波器电容Cf≤2×10-6F，选择滤波电容为0.2μF；电网频率f=50 Hz，PWM 整流器开关频率fsw=10 kHz，基于式（14）可得谐振频率fres的范围，选择fres=2 kHz；最后分别计算桥臂侧电感L1和网侧电感L2，由式（15）和（18）可得桥臂侧电感L1=0.5 mH，网侧电感L2=0.2 mH。

3.2 恒功率负载控制电路搭建

系统的电压外环控制均采用PI 控制，依据PWM整流器基本电路模型以及式（41）和（42），可得电压外环比例调节系数KvP=0.5，积分调节系数KvI=3.5。当电流内环采用PI控制时，系统的控制电路模型如图14所示。

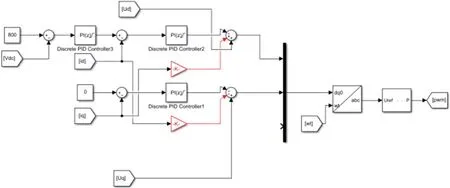
图14 电流内环为PI控制时的控制电路模型

当电流内环采用MPC时，系统的控制电路模型如图15 所示。电流内环控制通过式（21）和（22）可得到最佳预测电流，最终选取最优电压矢量ud、uq对应的开关状态，控制PWM整流器开关管的导通和关断。

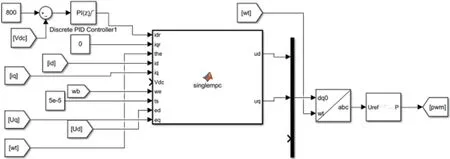
图15 电流内环为MPC时的控制电路模型

建立的交流恒功率负载系统参数如表1所示。

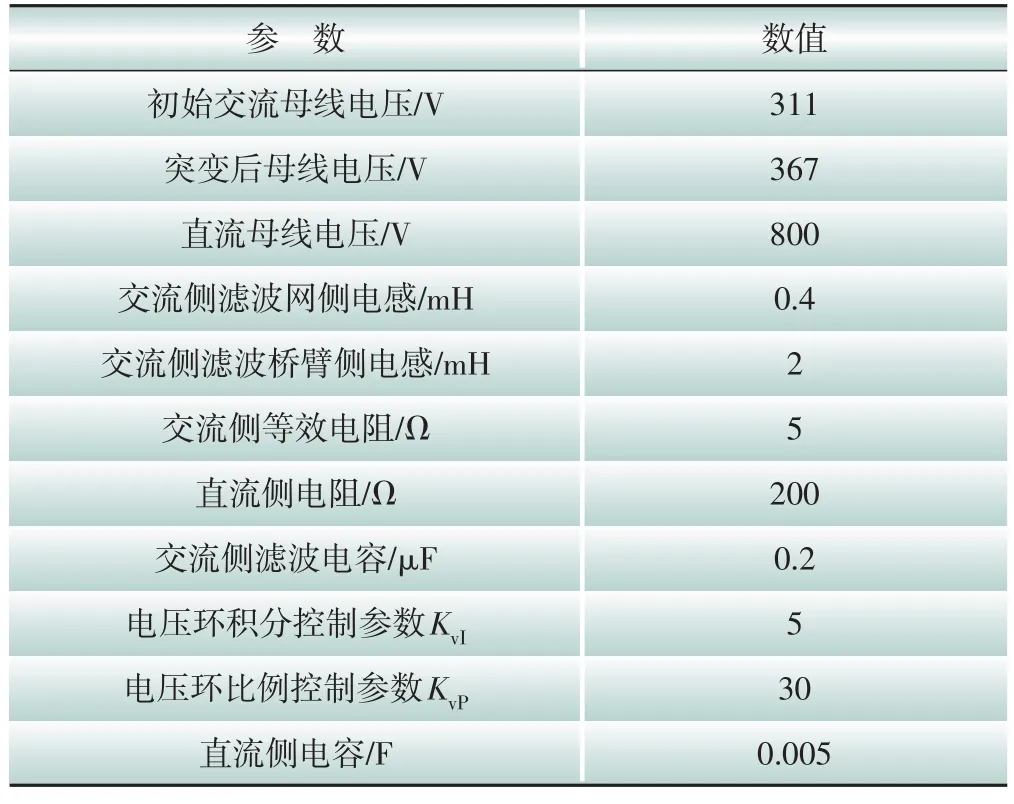
表1 系统仿真参数

根据表1 中的交流恒功率负载模型的系统参数，对系统的恒功率特性以及内环采用MPC对比PI 控制的动态优势进行仿真验证。首先在对系统的恒功率特性以及可以实现稳定控制进行仿真验证时均采用MPC。初始时刻交流母线电压输入有效值给定值为327 V，系统稳定运行且直流侧负载电压能稳定控制在给定值800 V，功率恒定，交流侧输入功率也保持恒定。在t=1 s时将交流母线的电压从311 V升至367 V，根据功率计算公式，本系统可认为功率因数为1，交流侧输入电压有效值上升，输入电流的有效值需相应调整下降，才能满足功率恒定。为了更直观地表现交流恒功率负载的负阻抗特性，将交流侧电压和电流经Park 变换后从d轴采样，即以有效值的形式表示，如图16所示。可以看出，此模型是准确的。

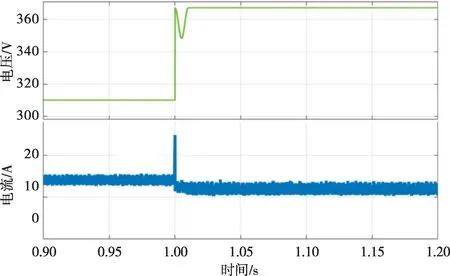
图16 交流侧电压、电流有效值

图17 为内环采用MPC 与内环采用PI 控制的直流侧电压曲线对比。可以看出，内环采用MPC时，直流侧电压可以更快达到给定值，并且超调明显更小。

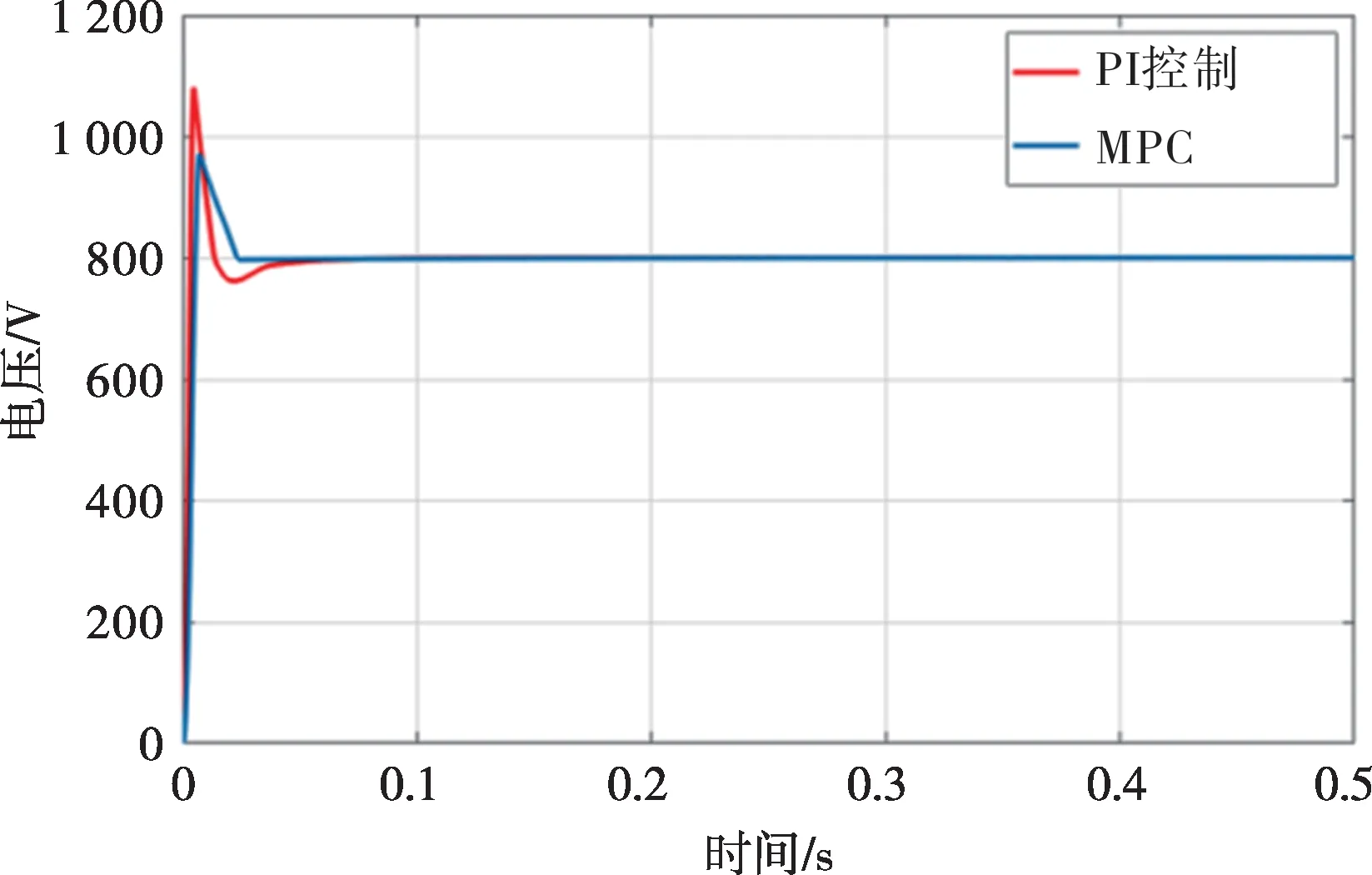
图17 直流侧负载电压对比

图18 为内环采用MPC 和内环采用PI 控制的直流侧功率曲线对比。当t=1 s 系统发生突变时，功率曲线均在母线电压突变之后短暂波动，并很快恢复到初始状态。经比较可得，当t=1 s系统发生突变时，采用MPC的系统鲁棒性更强且恢复速度更快。

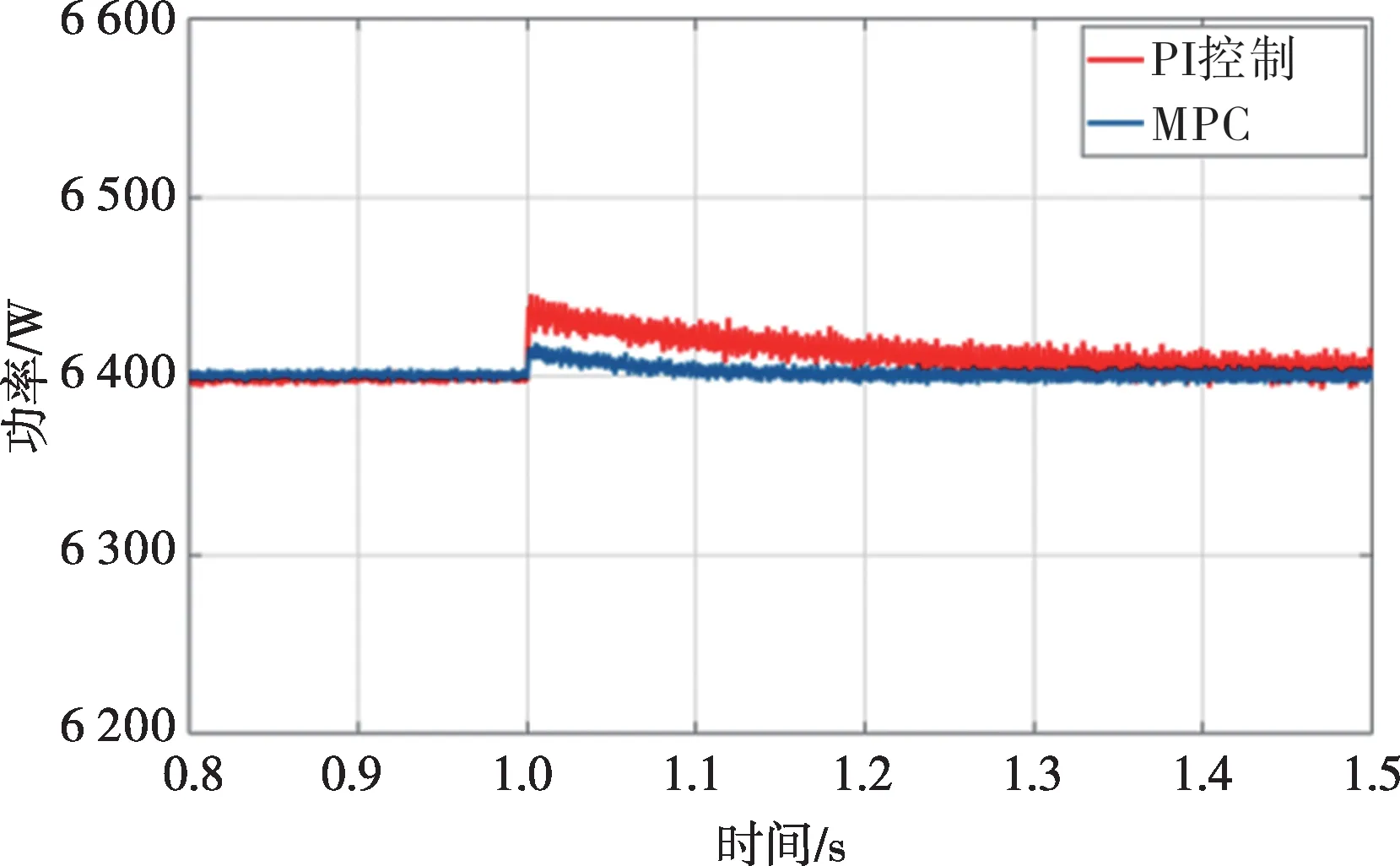
图18 直流侧负载功率对比

交流侧电流波形如图19 所示。可以看出，相较于传统LC 滤波装置，采用LCL 滤波装置时交流侧电流的波形质量明显更好。

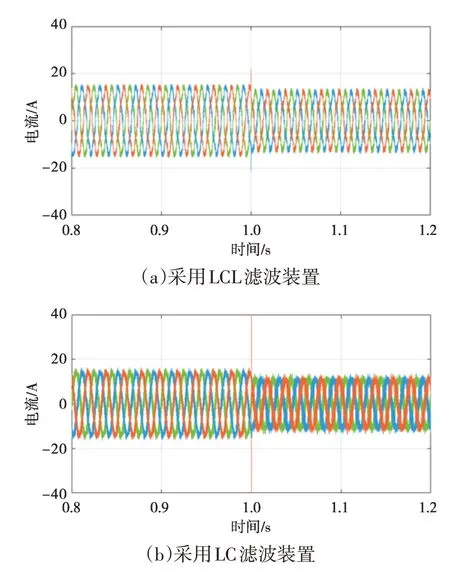
图19 交流侧电流波形

图20 给出了交流电流谐波分量，可以看出，采用传统LC滤波装置时交流侧电流谐波分量达到18.44%，而采用LCL滤波装置时交流侧电流谐波分量只有2.6%，THD（总谐波畸变率）小于5%，波形质量更好。

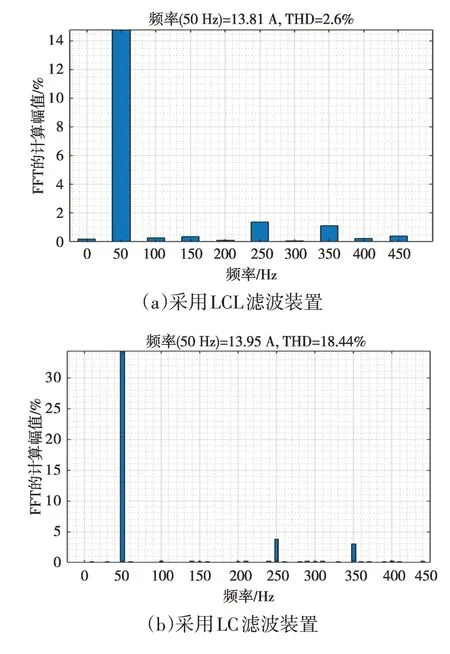
图20 交流侧电流谐波分量

4 结语

本文分别对滤波器和控制策略进行优化，基于PWM 整流器、电阻和LCL 滤波器，结合传统PI控制和MPC的优势，提出一种电压外环控制应用PI调节器、电流内环应用MPC、主电路设计加入LCL 型滤波器的交流恒功率负载模型。仿真结果表明：在物理层面，根据电感总量、电容和谐振频率设计的LCL 滤波器能够有效抑制交流侧电流谐波失真，提高电能质量；在控制算法层面，所提控制模型通用性强、动态响应快、超调较小、鲁棒性强，能够准确体现高性能电动机的动态特性，为电力系统动态性能分析提供必要保障。