分层强剪切环境下减阻板对圆柱减阻效应研究
2022-08-09傅依达王春凌
王 寅,傅依达,王春凌,张 洁,徐 明,计 勇
(1.南昌工程学院 水利与生态工程学院,南昌 330099; 2.江西省科学技术信息研究所,南昌 330046;3.台州学院 建筑工程系,浙江 台州 318000)
1 研究背景
层化水体常见于近岸及河口区域,温度、盐度的垂向梯度可导致水体密度分层[1]。微弱的外界扰动会在分层面(密度跃层)上引发携带巨大能量的内波[2]。内波所引发的强烈作用力可能对水下支撑柱状物造成严重的威胁[3]。
近岸地区开发逐年深入,随着大批跨海大桥以及近河口跨江大桥的建设[4],内波作用下桥墩的结构安全成为工程界极为关注的问题[5]。国内外学者通过开展大量柱体稳定的研究工作发现,当流体流经柱体时,从柱体两侧交替脱落的漩涡在增大柱体所受阻力的同时[6],还会产生作用于柱体上并垂直于主流方向的周期性振荡力[7]。此类振荡力极易降低结构物的强度并造成疲劳损坏[8]。
研究者尝试通过抑制流动分离和漩涡脱落以达到柱体减阻目的[9-10]。在柱体上游一定距离处放置减阻板是常见的被动减阻方法,该方法源自Morel和Bohn[11]的物理实验成果:当串列放置的两个柱体间距小到一定程度时,两柱所受阻力均小于单柱情况。基于该理念,Lesage和Gartshore[12]通过在上游设置一个减阻板,有效削弱了作用在下游柱体上的时均阻力以及振荡力。针对分层强剪切环境,Wang等[13]采用数值模拟研究了内波对串列双柱的作用效应,发现柱间距对柱周漩涡特性影响很大。Zhou等[6]就减阻板对柱体受力的削弱效果进行了数值模拟,通过改变板长以及板-柱体间距得到最优减阻工况。
目前,绝大多数柱体减阻研究仅在密度均一流环境中开展。内波环境和密度均一流环境的流场差异很大,内波在传播过程中,密度跃层上、下水体流动呈交替反向状态,会产生破坏性强大的剪切流动[14],迫使柱体承受附加作用力。研究分层流内波环境下柱体的减阻效应尤为重要,而相关研究鲜有所闻。本文将密度均一流环境下上游减阻板对柱体减阻的概念引入内波环境下的圆柱受力研究当中。借助三维数值大涡模拟(Large-eddy simulation(LES))模型研究无量纲减阻板板长(即阻塞比)l/D以及无量纲“板-柱”间距s/D对柱体减阻效应BR的影响机制,以及减阻效应的合理范围。
2 控制方程及求解方法
2.1 动量方程及连续性方程
基于连续假设,描述不可压缩黏性流体三维瞬态运动过程的Navier-Stokes方程(N-S方程)可表示为:
(1)
(2)
式中:ρ为密度项(g/cm3);t为时间(s);i(i=1,2,3)为笛卡尔坐标系的3个方向;xi为空间坐标;ui为流速项(g/cm);p为压力项;μ为动力黏性系数;fi为单位体积力。
2.2 标量输运方程
本文中,激发内波的分层水体是由上下水层的盐度变化引起的。两层水体之间的对流-扩散的效应可表示为
(3)
式中:C为标量体积浓度(kg/m3),0≤C≤1,通过公式ρ=Cρlow+(1-C)ρup可控制上下水层水体密度(ρlow、ρup分别表示上下水层密度);S为源项或汇项;k为扩散系数。
2.3 紊动模型
本文所采用的大涡模拟技术(LES)是对紊流脉动的一种空间平均,通过滤波函数将大尺度的涡和小尺度的涡分离开。过滤后的动量和质量方程(滤波函数用上划线表示)为:
(4)
(5)
(6)
(7)
3 数学模型
3.1 数值波浪水槽的建立及造波方法
本研究所建立的三维数值波浪水槽如图1所示。水槽的长(X)×宽(Z)×高(Y)为12 m×0.6 m×0.8 m。圆柱直径D=0.1 m,放置在水槽横向(Z)中心。坐标原点设置在左下前点,柱体底部中心坐标为:(x,y,z)=(6,0,0.3)m。本文采用重力塌陷法制造内波[16]。基于该方法,将水槽沿X方向分成造波区(x=0~0.7 m)和传播区(x=0.7~12 m)两部分,计算开始前先将整个水槽配置为上层清水(图1中的白色水体)及下层盐水(图1中的有色水体)、密度分别为ρ1和ρ2(ρ1<ρ2)的两层流体系统。
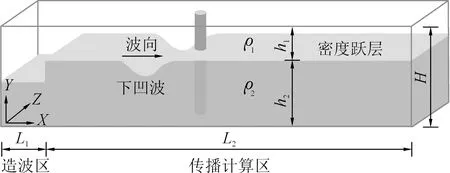
图1 数值模型布局及重力塌陷示意图Fig.1 Schematic diagram of generating internal solitary waves by gravity collapse in a stratified fluid tank
数值模型具体的参数设定为:ρ1=0.998 g/cm3,水层厚度h1=0.2 m;ρ2=1.017 g/cm3,水层厚度h2=0.6 m,总水深H=0.8 m。模型采用大涡模拟(LES)模拟下凹形内波的传播。采用有限体积法离散控制方程[17]。利用SIMPLE算法对流速—压力项进行耦合[18],保证了质量守恒,并以此得到压力场[19-20];扩散项采用二阶中心差分格式离散,对流项采用二阶上风格式离散;采用二阶隐式格式对时间项进行离散。造波区左端边界、水槽侧壁、水槽底部以及柱体表面均采用无滑移固壁边界。避免内波发生反射,水槽右端采用Sommerfeld辐射型边界。顶部采用“刚盖”假定,以此忽略表面波的影响[21]。水面波相较于内波而言非常小[22-23],因此采用“刚盖”假定处理水面是可行的[24-25]。
3.2 数值模拟结果与物理模型试验结果的对比验证
网格收敛性分析及物理模型试验对数值模拟的验证可参照笔者已刊出文献[26],文中单柱模型尺寸、边界条件(如图1所示)及工况设定皆与该文献一致。
4 减阻效应计算结果及分析
本研究在单柱模型基础上采用在上游放置减阻板的方法降低柱体阻力,减阻模型示意图如图2所示,减阻板通常为非流线体的钝体。本文选用长方体形状,板长为l,“板-柱”间距为s。圆柱所受的无量纲水平合力CFn定义为

图2 数值减阻模型示意图Fig.2 Schematic diagram of the numerical experiments on reducing forces
(8)
式中:Fn为数值模拟计算所得柱体所受水平力合力(N),可通过对作用于柱体侧壁的压强进行面积分得到;g为重力加速度(cm/s2);A为柱体的迎风面积(cm2);H为水槽总水深。
将柱体的减阻效果用减阻比BR表示,定义为
(9)
式中:CFn-single-max为无减阻板工作时,单柱所受无量纲水平力幅值;CFn-max表示各工况下无量纲水平合力幅值。BR=0~1,说明作用力被减阻板有效削弱,减阻板发挥减阻效应;BR为负说明当存在减阻板时柱体受力反而大于单柱工况,称为“减阻过度”;BR=0时说明有、无减阻板情况柱体受力相同,称为“减阻无效”。
研究共模拟了20组工况,令水深比h1/h2=0.33、上下水层密度差Δρ=0.019 g/cm3及波幅ηo/H=0.103保持不变,研究阻塞比l/D(l/D=1~0.25)以及“板-柱”间距s/D(s/D=1~2)对下游柱体减阻效应(减阻比BR)的影响机制,其中,ηo为内波波幅(m);ηo/H为无量纲内波波幅。具体工况见表1。同时对比在有无减阻板控制的情况下,柱周流场分布及柱体受力规律的异同,以研究不同工况减阻效应的差异并找到较好的减阻范围。数值模拟数据提取的特征时刻为柱体受力达到其峰值CFn-max所对应的最不利时刻。

表1 各工况详细参数Table 1 Detailed parameters in cases
4.1 最优减阻工况讨论
图3给出了柱体所受力幅值CFn-max与阻塞比l/D及“板-柱”间距s/D的对应关系。前文提到CFn-max表示内波无量纲水平合力幅值,从表1可知,该幅值在部分工况会出现负值。正值表示柱体受力方向与波传播方向一致,负值表示受力方向与波传播方向相反。若受力绝对值接近0,说明柱体受力很小。由图3可知,CFn-max随着l/D的增大呈递减趋势:减阻板越长,柱体所受阻力越小;对于同一l/D,CFn-max随s/D的增大逐渐恢复至单柱情况(CFn-single-max=0.338),说明板-柱间距越大,减阻效应越差。减阻效果最优工况为L0.5s1.25(l/D=0.5、s/D=1.25),此时柱体所受阻力|CFn-max|=0.114(图3中圆圈所示点);曲线L0.5(l/D=0.5)工况的减阻效果要明显优于其它3条。相反,曲线L1(l/D=1)工况受力很大且传播方向均与波逆向,逆向力极大,工程中应当避免。

图3 同l/D情况下CFn-max与s/D的对应关系Fig.3 Plots of CFn-max varied with l/D and s/D
4.2 柱体不同部位的减阻效果
内波和密度均一流最大差别在于:内波环境中上下水层的流速反向,上水层流向与波同向(在坐标轴上为正),下水层则反向。同时,减阻板的存在对柱体不同部位的影响各异。因此,本研究将柱体沿垂向分成8段(每段0.1 m):位于上水层的部位称之为“上部”,位于下水层的部位称之为“下部”。以密度跃层为界,分界面在0.6 m处。
以工况L0.5s1.25(l/D=0.5,s/D=1.25)作为典型工况,将其与无减阻板控制的单柱工况进行对比。定义Cf为柱体各分段的无量纲水平合力,其表达式只需将式(8)中的Fn用f替代即可。当总水平合力达到其峰值时,各Cf垂向分布如图4所示。在工况L0.5s1.25下,上部的Cf为负值且绝对值均小于单柱情况。但在下部,两者受力分布几乎重合。说明减阻板的减阻效应只在上水层中生效。通过对比图5有无减阻板情况下的柱周压强分布来对该现象进行说明。图5(a)、5(b)分别给出了上部(h=0.7 m)和下部(h=0.3 m)的压强分布。由图5可知,上部的压强分布变化显著,而下部几乎没变。减阻板对不同部位产生不同效果的原因可总结为以下两点:①下部流速相较上部小得多,导致下水层的减阻效应弱;②下水层流向与上水层及波向相反,减阻板位于柱后的涡街里,减阻板对下水层不起作用。

图4 单柱工况和L0.5s1.25(l/D=0.5,s/D=1.25)工况Cf对比Fig.4 Comparisons of Cf between the case of single pile and case L0.5s1.25(l/D=0.5,s/D=1.25)

图5 单柱工况和L0.5s1.25(l/D=0.5,s/D=1.25) 工况压强分布对比Fig.5 Comparisons of pressure distribution between the case of single pile and case L0.5s1.25(l/D=0.5,s/D=1.25)
5 分析与讨论
5.1 深入讨论减阻板对柱体的减阻效应
本节将基于不同的l/D和s/D进一步分析柱体的减阻效应。据上节研究可知,减阻板对柱体下部的影响很小。故以下只讨论上水层h=0.7 m水深处的流场、压强分布及合力。
5.1.1l/D和s/D的改变对流场的影响
以工况L0.5(l/D=0.5)为例研究板-柱间距s/D对流场的影响,不同s/D情况下柱周涡量分布如图6所示。对比图6(a)、(b)、(c)以及图6(d)单柱情况可知,减阻板的背流面会产生明显漩涡区。当减阻板与柱体相距较近(见图6(a)),柱体处于板后漩涡区中,板、柱后联合形成更大的漩涡区,柱体完全浸没于漩涡中。随着s/D的增大,柱体逐渐远离板后漩涡区,如工况L0.5s2(l/D=0.5,s/D=2)(图6(c))所示,柱体几乎不再受前方漩涡的影响,流场状态逐步恢复至单柱情况。

图6 l/D=0.5、h=0.7 m时柱周流场及涡量分布Fig.6 Flow fields and vortexes around the pile in cases l/D=0.5 at h=0.7 m
减阻板阻塞比l/D的影响如图7所示。图7(a)、图7(b)对比了工况L0.5s2(l/D=0.5,s/D=2)和L1 s2(l/D=1,s/D=2)的涡量等值线。l/D对板后漩涡区有较大影响。当减阻板较短(见图7(a)),板后漩涡区较小,对后柱几乎没有影响;当减阻板较长(见图7(b)),板后涡区不仅影响到柱体上游侧,同时对柱后涡区也起到了抑制作用。

图7 s/D=2、h=0.7 m时柱周流场及涡量分布Fig.7 Flow fields and vortexes around the pile in cases s/D=2 at h=0.7 m
5.1.2 漩涡区对减阻的影响
减阻板后涡区的改变会影响柱周涡量的变化。继续对比工况L0.5s2(l/D=0.5,s/D=2)、工况L1s2(l/D=1,s/D=2)以及单柱工况,水平受力系数Cf的垂向分布如图8所示。工况L0.5s2和单柱工况下柱体上部受力分布十分接近。由图7(a)可知,两工况受力分布接近的原因在于柱体几乎不再受板后漩涡的影响。相对的,工况L1s2(l/D=1,s/D=2)中柱体上部在减阻板的影响下受到的Cf为负值。

图8 s/D=2时Cf垂向分布Fig.8 Vertical distribution of Cf in cases s/D=2
下面将根据所提取的柱表压强分布(h=0.7 m)进一步分析减阻效应。不同工况下柱表压强分布见图9。由图9可知,工况L1s2(l/D=1,s/D=2)中柱体前侧的压强明显小,背侧压强略大。这是由于工况L1s2中柱体前侧受到板后漩涡的影响,背侧漩涡受到抑制,如图7所示。前侧压强小于背侧压强,导致柱体受到逆波向的压差,并产生负的Cf(见图8)。综上所示,板后漩涡极大影响了柱体的受力。
图9 s/D=2、h=0.7 m时柱周压强分布Fig.9 Pressure distribution along the cross section of pile in cases s/D=2 at h=0.7 m
由此断定,减阻参数l/D、s/D决定了板后漩涡区的大小和位置,而柱周漩涡是影响柱表压强分布的根本原因。换而言之,减阻参数的变化最终影响柱周漩涡并改变了柱体的受力。
5.2 减阻效应的量化分析
减阻板能降低内波对柱体的作用力,这并不代表同样会降低柱表压强。一味地增大l/D或减小s/D可增强柱前涡区,导致柱体前侧压强远小于背侧。由此就可能在下凹形内波环境下激发逆向作用力,简称为“逆阻力”,如工况L1(l/D=1)所示。
图10给出了柱体减阻比BR与s/D及l/D的相关关系。由图10可知,在“LineA”与“LineB”之间区域,减阻比BR≥0.2,减阻效果较好,为有效减阻区。其中,在0.4≤l/D≤0.55,1.15≤s/D≤1.25内(图10中的“ZoneA”)减阻效果最佳。对于“LineC”以上区域,减阻比BR<0。说明此时上游板非但未起到减阻效果,反而增大了柱体所受到的阻力,要尽量避免。整体来说,BR与l/D和s/D都保持着较好的相关性。

图10 BR与s/D及l/D的相关关系Fig.10 Plot of BR varying with s/D and l/D
式(10)为采用回归分析所构造出的经验公式,给出了减阻比BR与s/l的拟合关系。两者具有较强的相关性,不同区间的表达式为:
(10)
以上3个方程将计算区间划分成3部分。①LF区:BR与s/l呈线性关系;②EF区:BR与s/l(42(位于EF区和TF区)时,BR>0,减阻板可发挥减阻效应。

图11 BR与s/l的相关关系Fig.11 Plot of BR varying with s/l
6 结 论
本文借助三维数值波浪水槽,把减阻概念引入下凹形内波环境中的圆柱受力研究中。研究了无量纲减阻板阻塞比l/D以及“板-柱”间距s/D对柱体减阻效应(减阻比BR)的影响机制,得到以下结论:
(1)在下凹形内波环境中,减阻板对上层水体柱体的受力及压强分布影响较大,而对下层水体柱体的影响极小。
(2)减阻板背部的漩涡区是产生减阻效应的根本原因。减阻板阻塞比l/D及“板-柱”间距s/D决定了漩涡区的尺寸和位置,并直接影响减阻效果。
(3)当柱体位于板后漩涡区中,柱体迎风面的压强明显降低,从而削弱了内波对柱体作用力。若柱前漩涡区过大,柱体将受到一个逆波向的作用力。
(4)利用减阻比BR量化了减阻效果。当l/D较大且s/D较小时,BR<0,称为“减阻过度”。此时,减阻板的存在反而增大了柱体受力;当0.4≤l/D≤0.55,1.15≤s/D≤1.25,BR较大,减阻效果优。
