电动振动台运动部件的特性分析与仿真

2022-08-08秦亚明鲍俊宇孙险峰

工程与试验 2022年2期

秦亚明，鲍俊宇，孙险峰

(1.北京航天希尔测试技术有限公司，北京 100075；2.中机试验装备股份有限公司，吉林长春 130103)

1 引言

电动振动台是传统的试验测试平台，通过运动部件的往复运动将电能转化为机械能，从而完成正弦扫频、随机、冲击(冲击响应谱)及波形复现等相关试验与验证，是目前国内外应用较为广泛的试验设备。谐振频率、使用频率范围、横振比、均匀度等是电动振动台的关键指标，这些指标均由运动部件的结构决定。运动部件的谐振频率与使用频率越大，电动振动台的试验能力越强。如何通过增加约束或改变运动部件的结构等方式有效地降低运动部件台面的横振比与均匀度，这是运动部件结构设计的难点。

以往通过两自由度物理模型的简化与经验估算方法获得运动部件的谐振频率，从而完成样机的设计、制造及测试，再根据测试结果不断地对运动部件的结构进行改进，从而获得较为理想的电动振动台的性能。但是，运动部件的横振比、台面均匀度等性能参数无法通过计算提前获得，这会影响振动台的设计效率，并增加研发的成本。为解决上述问题，本文利用模态与动态频率响应方法，对运动部件的主要参数进行仿真，并与测试结果进行比较，将有限元方法应用于运动部件的结构设计中。

2 物理模型及简化计算方法

运动部件由运动骨架(一般为铸铝或铸镁合金)与按顺序绕制的具有一定匝数的铜或铝制线圈组成。运动骨架与线圈通过高温固化工艺粘接牢固，两者之间的刚度较大。为了计算方便，将这两部分看作连续的系统，并将其简化为由m1、m2及k1、k2组成的一个集中质量的两自由度振动系统。求解电动振动台运动部件的共振频率f，用机械等效原理进行简化[1]，模型如图1所示，其中，m1为运动骨架质量；m2为线圈质量；k1为悬挂系统刚度；k2为运动部件刚度。

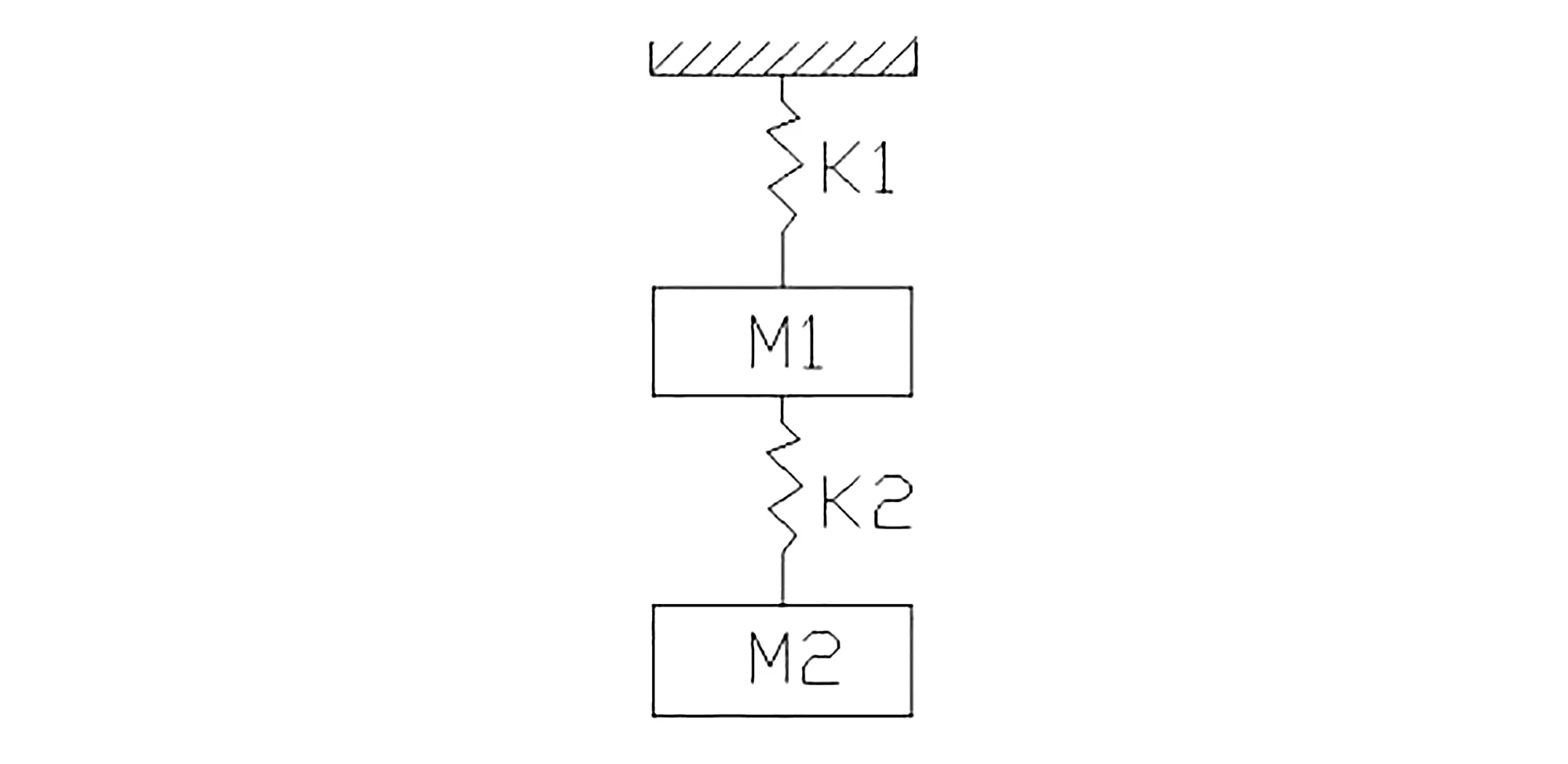
图1 动圈模型

运动部件谐振频率是：

运动部件的刚度是由运动骨架与肋板的拉、压刚度以及弯曲刚度组合，从而得到运动部件的等效刚度：

其中，E为材料弹性模量；t为肋板厚度；H为动圈高度；D为动圈直径。

由上式可知，运动部件刚度的大小与材料弹性模量E和肋板厚度t成正比，还与运动部件的结构尺寸等有关。要提高连接刚度，应选择比重小、阻尼大、弹性模量高的镁或铝合金材料，还需要优化运动部件的结构，从而使其谐振频率最大。

以40kg的激振器为例，利用以上简化公式计算运动部件的谐振频率为4114Hz，而实测运动部件的谐振频率约为4500Hz，计算值与实测值的误差约为8.6%，说明利用简化方法得到的谐振频率误差较大。

3 模态分析

模态分析是用有限元法对振动结构离散化，建立数学模型，求解系统特征值，通常不考虑系统阻尼。特征值和特征矢量为系统各阶固有频率和固有振型的矢量。振动方程可表示为：

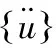
无阻尼下，可得到n个方程特征值λi(n阶自由度)：

([K]-λi[M]){u}=0

特征值一般采用Lanczos算法求解，得到低阶特征值λi，从而求得固有频率fi：

(1)动圈模型的建立。线圈部分由内、外两层铜线在专用模具下绕制成筒形，在中间夹入厚度为0.2mm的不锈钢带，利用特殊环氧树脂胶将铜线与钢带粘接牢固，将驱动线圈与不锈钢带两部分作为一整体，其有单独的弹性模量E与泊松比μ。

(2)前处理。将运动部件的复杂实体进行简化，然后剖分实体成为规则的六面体模型，共划分出332个六面体模型。对网格优化处理后，形成三维六面体实体网格，模型划分后有49422个节点，14704个六面体网格。

(3)约束条件与边界条件。运动部件通过靠近台面上部的两组板簧悬挂在台体上，除了具有一定承载能力外，还约束了运动部件的旋转和摆动，从而使运动部件只存在一个Z向的自由度。在有限元中模拟时采用多点约束单元(MPC)，仅保留Z向平动，并与Z向弹簧连接，弹簧底部固定约束六个自由度。在上、下两组板簧的孔边采用约束单元(MPC)与中心孔连接，上、下两组中心孔用RBE2结构建立关系。动圈约束及网格划分见图2。

图2 动圈约束及网格划分

(4)材料属性。运动骨架是用铝合金(LC4)材料加工而成。驱动线圈部分由内、外两组铜线与不锈钢带粘接而成，其连接紧密，在振动过程中不会发生脱落。由于不锈钢带的作用，线圈内部刚度增加。采用材料的特性如表1所示。

表1 材料特性

(5)后处理及分析。第1阶频率为5.69Hz，其是在底部支撑弹簧的作用下动圈整体Z向移动的共振频率，频率值与等效的弹簧系数值有关。第2阶是因绕运动部件轴向扭转，第3、4阶是前、后、左、右4个方向摆动而形成的，第5阶是线圈部分的呼吸效应引起台面局部振动，第6、 7阶是运动部件左右扭转振型，第8阶是运动部件的呼吸效应引起的，第9阶是运动骨架发生扭转。从第9阶开始，由于运动部件横向扭转与呼吸效应相互叠加更趋明显，台面谐振加剧。观察模态前30阶固有振型，第28阶振型是沿动圈Z向伸缩振动，这是运动部件的谐振，频率为4481.5Hz。各阶模态如图3所示。

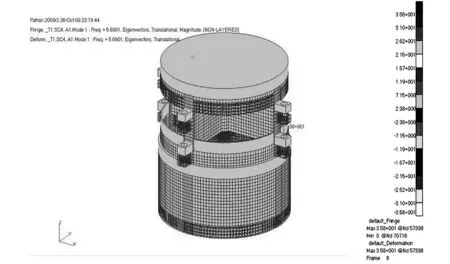
(a)第1阶

(b)第2阶

(c)第3阶

(d)第5阶

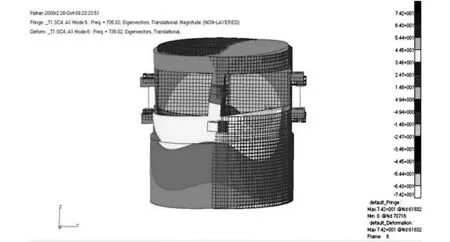
(e)第6阶

(f)第8阶

(g)第9阶

(h)第28阶

(6)试验验证。利用LDS LASER(8通道)控制仪，1个控制传感器位于运动部件中心，4个监测传感器位于运动部件的最外圈成90°分布，运动部件空台做扫频(5～5000Hz)测试，测试结果如图4所示。可以看出，谐振频率为4487Hz。

4 振动台频率响应分析

根据振动台的原理，如果在线圈部分施加一个正弦激振力谱，则此力通过运动骨架的肋板传递到振动台的工作面，使台面产生频率响应。考虑动圈在近似线性状态下工作，可以认为，任一频率下的正弦激振力都可以与台面上的加速度响应成线性关系。

当电压、电流一定时，振动台的驱动力是确定的，且与电压、电流成线性关系，而力与台面加速度之间的关系是随频率变化的函数，即传递函数。

图4 扫频试验

其中，F(f)为驱动力谱，a(f)为控制点加速度谱，H(f)为传递函数。

在频率响应分析中，须先求出传递函数，然后反推出控制条件下的力谱，最后再计算台面控制点的响应。

(1)施加等效载荷。利用模态分析的网格与约束条件，对线圈部分施加激励，即施加固定正弦激振力谱，在运动部件台面上会得到相应的加速度频率响应。调整正弦激振力谱的大小，从而得到所需要的恒流频率响应曲线。

(2)运动部件频率响应仿真与试验数据比较。将仿真结果与测试曲线进行数据比较(如图5所示)，可以看出，恒流特性曲线与实测曲线在全频率段基本是一致的。曲线有两个峰值，第一个峰值为弹簧悬挂系统对应的固有频率f1，第二个峰值对应运动部件的谐振频率f2。两个峰值之间是比较平坦的区域，为电动振动台的工作频率区域。在频率4500Hz附近时达到运动部件的谐振频率(与模态仿真一致)，在频率5100Hz、5400Hz附近出现了局部反共振与局部共振现象，在频率6100Hz时达到一阶反共振点，共振与反共振的趋势与实测值极为相似。故仿真的意义在于，可以在设计阶段初步了解运动部件的动力学性能指标。

图5 频率响应仿真与实测比较

(3)运动部件扫频仿真。对运动部件进行扫频仿真是进行频率响应分析的主要应用之一。以运动部件空台试验为例，将正弦激振力谱分段调整，力谱在相应位置产生的响应曲线与控制点(传感器1)曲线吻合，在台面外侧可求出频率响应，同时与测量点(传感器2)响应曲线进行比较(如图6所示)，可以看出，扫频、仿真与测量频率响应曲线之间基本一致，能很好地反映出振动台的实际工作情况，其值就是振动台台面均匀度。