基于遗传算法和场域模型的多障碍物房间人员疏散研究*
2022-08-08陈菲菲彭立志周宗财朱孔金
陈菲菲,彭立志,周宗财,朱孔金
(合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)
0 引言
影剧院、体育馆看台、教室等公共场所核心区域一般为规则排列座椅,部分座椅间留有过道供行人进出,该类型房间称为多障碍物房间,具有人员密度高、行人移动不方便等特点,当发生紧急情况需要进行人群疏散时,座椅成为疏散路线的障碍物,房间内部座椅和过道布局对人群疏散效率影响显著,甚至威胁行人生命安全。因此,对多障碍物房间布局进行优化设计,对提高疏散效率、保障行人安全具有重要意义。
目前,针对多障碍物房间行人疏散研究主要通过实验和仿真分析公共场所内行人运动特性和疏散规律,而通过疏散效率为导向对多障碍物房间进行布局优化的研究相对较少。Guo等[1]通过对教室进行实验仿真研究发现良好能见度和零能见度条件下行人进行疏散的路径选择行为;Chen等[2]对儿童在非紧急情况下的疏散行为进行研究,并建立元胞自动机模型模拟有群体行为和无群体行为的儿童运动。部分研究考虑房间出口布局和桌椅布局对行人疏散的影响:Delcea等[3]通过传统教室疏散实验,研究随机设置障碍物和志愿者引导对疏散的影响并建立Agent模型;董力耘等[4]建立基于动态势能场的元胞自动机模型,对3种不同出口宽度和4种类型桌椅布局进行研究,发现无论何种布局,行人更偏向于选择距离最近出口进行疏散;Zhu等[5]对多障碍物教室进行行人疏散实验,考虑主通道对疏散影响基础上改进元胞自动机模型;刘莹等[6]通过Pathfinder软件对体育馆进行疏散仿真,研究各疏散口分布、通道分布、疏散方式等对疏散效率影响。上述研究主要针对几种典型布局方案进行比较分析,对房间内部过道布局方案考虑不够全面。
遗传算法通过计算机仿真将求解问题过程转化成生物进化中染色体基因交叉、变异过程。面对较复杂的问题,能够快速获得优化效果,诸多研究均将其引入行人疏散研究中:张惠彬等[7]利用遗传算法对人员疏散路径进行优化,得出疏散距离、道路通行难易程度和化学毒剂扩散情况均会影响行人疏散;韩雨烔等[8]建立遗传算法和行人运动仿真模型的双层优化框架,对3种典型建筑出口布局进行研究,分析出口宽度、人员半径、初始人员密度对疏散效率的影响;贾进章等[9]利用遗传算法全局搜索能力快速处理蚁群算法初期所需信息素,采用蚁群算法快速找出可行路径,减少路径生成时间,提高疏散效率。
因此,本文针对多障碍物房间内部座椅布局设计问题,以行人疏散效率为目标导向,综合行人疏散场域模型和遗传优化算法,设计1种能够寻求多障碍物房间座椅布局的优化方法,进而提高行人在多障碍物房间的疏散效率。研究结果可为多障碍物房间的布局设计提供建议。
1 模型与算法
1.1 疏散模型
本文采用改进的元胞自动机场域模型[10]进行行人疏散仿真,离散元胞大小为0.4 m×0.4 m,元胞类型包括能够被行人占据的过道/出口空闲元胞以及不能被行人占据的座椅/墙壁障碍物元胞。行人按照转移概率可以向上、下、左、右4个相邻可行空闲邻域元胞运动,每个时间步最多只能移动1个元胞。转移概率由所处元胞及相邻元胞的静态和动态场域值确定,所有行人移动采取随机更新规则。
利用静态场与动态场计算转移概率如式(1)所示:
Pij=Nexp[Ks(Sij+ΔSij)]exp(KdDij)(1-nij)μij
(1)
式中:Pij为转移概率;N为归一化系数;Sij为静态场值;ΔSij为静态场增加值,在现实中当行人移动到通道时,很少再进入狭窄的座椅过道区域,为增加通道对行人的吸引力,在原有静态场基础上增加横纵向通道元胞的静态场值;Ks,Kd分别为静态场和动态场的敏感系数,取值范围为0~1;Dij为动态场值;nij为用以判断元胞是否为可行空闲元胞,若被其他行人占据,则取值为1,反之为0;μij为元胞类型标识,若元胞是障碍物元胞,则取值为0,若为空闲元胞则取值为1。
静态场是用来描述行人对疏散环境的熟悉程度,其与房间内部布局有关,大小与元胞和出口距离成反比,并且在疏散过程中固定不变,如式(2)所示:
(2)
式中:em为第m个出口,m=1,2,3,…;xi0,yi0分别为第m个出口的横纵坐标;xij,yij分别为当前元胞的横纵坐标。
动态场是用来表示所有行人经过元胞的吸引力,可反映在恐慌状态下行人的从众行为,动态场值是动态变化的,随时间步推移会以一定概率衰减并向周围扩散,包括以下4个计算步骤:
步骤1:初始化所有空闲元胞的Dij=0。
步骤2:当有行人经过元胞(i,j)时,元胞(i,j)下个时间步的动态场值增加1,如式(3)所示:
(3)
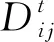
(4)


(5)
1.2 优化算法
大规模的多障碍房间其内部布局方案较多,因此本文采用遗传算法寻求基于疏散效率导向的布局最优方案。优化流程如图1所示。

图1 多障碍物房间的布局优化遗传算法流程
遗传算法中每条染色体中的编码个数代表1排座椅列数与过道数之和,用0表示座椅,1表示过道。为贴近实际情况,本文座椅列数和过道数设置为至少有2列相邻。优化目标函数选适应度函数,算法步骤如下:
步骤1:初始化种群。随机产生M个初始过道布局方案,并根据行人疏散模型计算出每种方案对应的时间步。给定交叉概率Pc、变异概率Pm以及迭代次数N。
步骤2:适应度计算。时间步越小说明其疏散效率越快,对应染色体应当有更大的空间和更多的机会被选择,适应度函数如式(6)所示:
(6)
式中:F(i)为第i条染色体的适应度;step(i)为第i条染色体对应的时间步。
步骤3:选择。根据轮盘赌从初始种群中随机选择2条染色体作为父代,如图2所示。
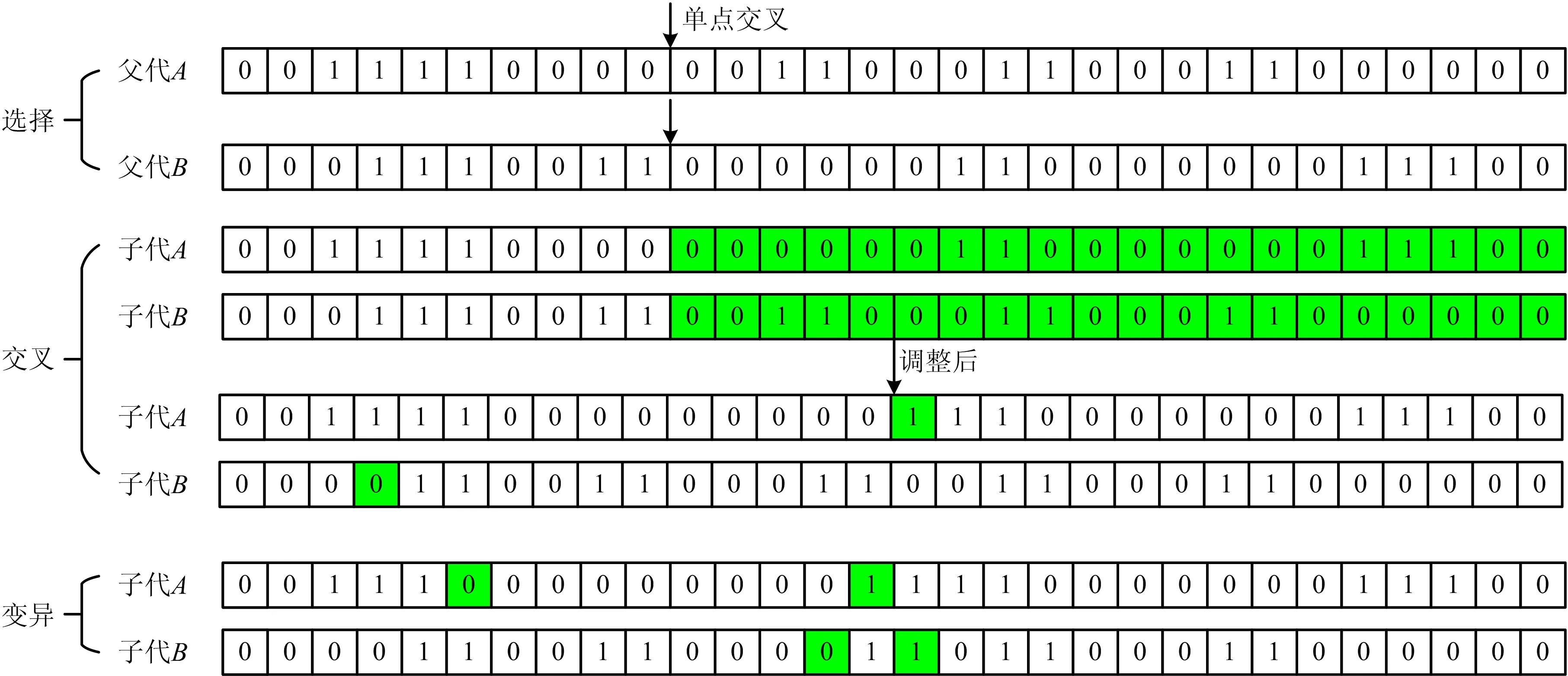
图2 遗传算法的交叉变异示意
步骤4:交叉。对2条父代染色体,按照概率Pc进行单点交叉。发生交叉后的2条子代染色体可能会出现以下2种问题:总过道数与总座椅列数与初始设置个数不同;会出现单独的座椅列或过道。当遇到以上2种情况时,要对产生的子代重新进行修改。以判断过道数为主,若过道数比初始设置增多或减少,均随机选择位置减少或增加过道数,使过道数和座椅列数与初始设置相同;若出现单独的座椅列或过道,则重复步骤3~步骤4,直到没有单独的座椅列或过道。
步骤5:变异。将步骤4中产生的2条子代染色体按概率Pm进行变异,得出2条新的子代染色体,若出现有单独座椅列或过道时,重复步骤3~步骤5,直到没有单独的座椅列或过道。
步骤6:计算新的时间步。将新的2条染色体代入行人疏散模型,计算对应时间步并比较大小,保留较小的时间步S(k),S(k)表示第k次迭代的最小时间步。
步骤7:迭代。重复步骤3~步骤6,在每次迭代中,比较S(k):若S(k) 仿真场景示意如图3所示。本文选用多障碍物房间划分88个×56个元胞格点,黑色格点为障碍物型元胞,代表桌椅或墙壁;白色格点为空闲元胞,可供行人占据和移动,房间内部座椅数量固定为40个×40个,最多可容纳1 600人。纵向通道总宽度为6.4 m(16个元胞宽度),房间前后分别设有与房间出口等宽的横向通道。房间出口宽度均为1.6 m,分别考虑2种典型的房间出口布局,如图3(a)~(b)所示。 图3 仿真场景示意 遗传算法中初始种群为50,迭代次数为300,Pc=0.8,Pm=0.1。场域模型中Ks=0.5,Kd=0.5,α=0.05,β=0.5,ΔSij=10。考虑最危险的情况,房间内有1 600人需进行紧急疏散,设置90%的人完成疏散表示疏散完成,每组工况共运行50次,取时间步最小的1组作为研究对象。 2出口房间和4出口房间疏散时间步随迭代次数变化情况如图4所示,疏散时间步随迭代次数的增加而迅速降低收敛,2出口房间疏散时间步由482降低至366,优化24%;4出口房间的疏散时间步从291降低至232,优化20%。相比2出口房间,4出口房间下的疏散时间步收敛较快。 图4 遗传算法中迭代次数与时间步关系 疏散时间步最优时对应多障碍物房间过道布局结构如图5所示。由图 5可知,对2出口房间,靠近出口侧的宽过道有利于行人疏散,较长的连排座椅宜布置在远离出口侧;对4出口房间,通过设置较多数量过道,较长连排座椅布置在房间中间侧,更有利于行人疏散。基于遗传优化算法获取的最优房间布局与常见布局方案存在差别,后者为对称结构,且分布较为均匀,如图3所示。 图5 遗传算法迭代后最优布局 为深入分析不同布局结构对行人疏散过程的影响,对比分析4种布局结构下的行人疏散过程,随机仿真50次的疏散时间步分布如图6所示。4种布局结构下行人疏散时间步统计分析见表1,无论2出口房间或4出口房间,优化算法获取的房间布局结构下的疏散时间均低于常见房间布局结构下的疏散时间,P1的平均时间步比P2的平均时间步减少66,而P3的平均时间步比P4的平均时间步减少42。 表1 4种工况下的疏散时间步对比 图6 4种工况仿真次数与时间步关系 2出口房间内通过各个出口完成疏散人数和房间内剩余人数随时间的变化情况如图7(a)~(b)所示,疏散早期阶段,各出口完成疏散的人数随时间近似线性增加,房间内剩余人数也近似线性降低,不同布局结构下仿真结果差别较小;疏散后期阶段,不同布局结构下的仿真结果开始出现显著差别,P1结构下行人疏散效率比P2结构下优势更加明显。原因可能是多障碍物房间内的行人疏散过程划分为出口控制阶段和过道控制阶 段,在疏散早期,距离出口较近的行人几乎同时到达出口附近,使得到达出口的行人数量超过出口通行能力,出口迅速达到饱和状态,疏散效率主要受出口通行能力的限制;疏散后期,距离出口较远的行人到达出口的时间有明显差别,出口通行压力得到缓解,此时疏散效率主要受到达出口的行人数量限制。4出口房间内通过各出口完成疏散人数和房间内剩余人数随时间变化情况如图7(c)~(d)所示,规律与图7(a)~(b)基本一致。表明多障碍物房间的内部布局结构在疏散后期阶段对疏散效率的影响更大,可通过调节到达出口的人群规模以优化多障碍物房间的整体疏散效率,使布局更加合理。 2出口房间与4出口房间在不同时间步下房间内行人疏散场景如图8~9所示。在疏散早期,2出口房间和4出口房间均会在出口附近、靠近出口过道和座椅过道内发生堵塞,随房间内人数减少,座椅过道内的行人逐渐疏散到横纵向过道中等待疏散。疏散后期,P1,P3的行人疏散与P2,P4明显不同,P1,P3的出口附近到达人数持续不断,疏散效率较高;P2,P4的行人主要分布在离出口较近的纵向过道中,出口附近的行人较少,图8~9很好地验证图7中P2,P4疏散后期疏散效率降低的原因。因此,合理的房间布局结构能够控制到达出口的人数,保持稳定的疏散效率。 图7 各出口疏散人数和房间内剩余人数随时间步变化 图8 P1和P2在不同时间步下房间疏散场景 图9 P3和P4在不同时间步下房间疏散场景 1)基于场域元胞自动机模型并融合经典遗传算法,对多障碍物房间的内部布局进行优化设计,并将优化后布局与常见布局进行对比分析。 2)当有较长的连排座椅布置在远离出口侧,过道主要布置在出口附近时,多障碍物房间疏散效率将得到提高。 3)合理的座椅布局设计可以协调疏散人群到达出口时间,控制到达出口行人数量,缓解出口通行压力,进一步提高整体疏散效率。 4)通过对不同布局进行对比分析,发现多障碍物房 间的内部布局对疏散后期的疏散效率影响较大,合理的座椅布局可保持疏散效率的稳定性。2 结果与分析
2.1 场景设置

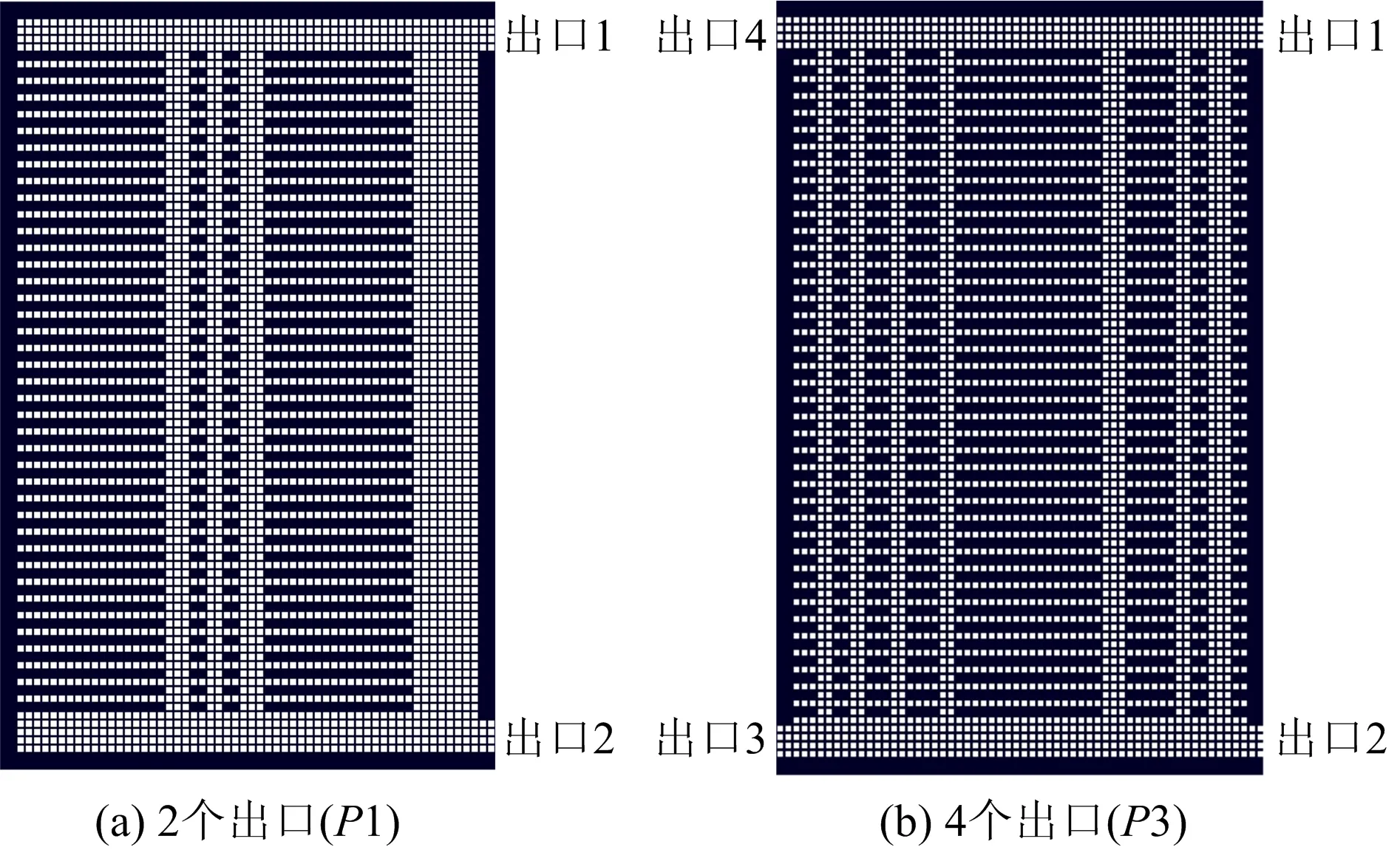
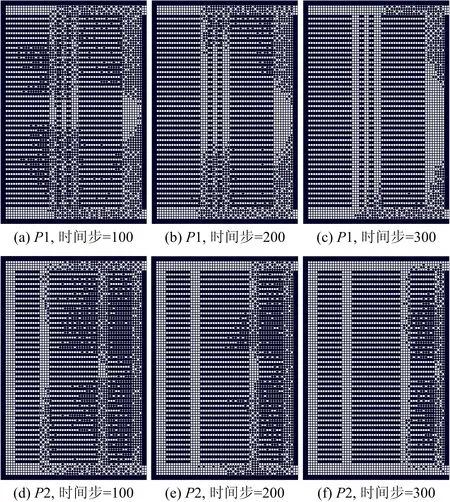
2.2 结果分析





3 结论
