耦合CPG神经网络的节律分析

袁泉, 徐洁琼, 陈慧莹

(1.广西大学 土木建筑工程学院, 广西 南宁 530004；2.广西大学 数学与信息科学学院, 广西 南宁 530004)

0 引言

在动物与环境的互动中,包括许多基本的重复行为,如呼吸、行走、爬行、游泳、咀嚼、抓挠等,这些重复行为由不同神经元集群的节律运动的协调作用而产生。生物学家认为动物的节律运动是神经中枢的一种自激产生的振荡行为,产生节律活动的神经环路被称为中枢模式发生器(central pattern generator,CPG)[1]。1911年,Brown[1]提出脊髓运动CPG的半中心振荡模型,该模型被广泛应用于各种重要运动节律的产生和控制中。例如,Rubin等[2]利用几何动力系统方法分析突触耦合的神经元网络集群节律的产生,表明快速抑制耦合将产生同步节律。

研究表明,节律运动是CPG的一种自激产生的振荡行为,但随着外界驱动的改变,运动节律模式会相适应地改变。不少学者逐渐研究外界刺激对CPG运动节律模式的变化。Whittington等[3]在实验中观察到抑制耦合的2个神经元网络的同步振荡是由谷氨酸受体激活引起的。Traub等[4]通过实验与理论分析再次验证谷氨基酸将影响神经网络的同步,并发现神经元的放电频率呈单调变化,只有当突触电流在合理范围时,突触传递将为同步振荡提供一个合适的机制。Xu等[5]基于相关系数讨论了同步振荡与同步程度之间区别与联系,发现在不完全同步振荡时可能会发生弱相位同步。

而谷氨酸一般可以刺激2种突触受体:一种是alpha-amino-3-hydroxy-5-methylisoxazole-4-propionic acid(APMA)；另一种是N-methyl-D-aspartic(NMDA)。Talpalar等[6]通过对转基因小鼠脊髓神经元加入NMDA,发现神经元的兴奋程度对NMDA有很强的依赖性,还比较了在增加与删除V0类中间神经元时对CPG运动节律的差异,最终表明神经元振荡频率由NMDA浓度调节。杨永霞等[7]通过控制兴奋性耦合神经网络的发放模式和呼吸节律,分析了CPG的动力学机制。孙燕等[8]讨论了中枢神经系统中一类神经元的表达模式与释放特性。Molkov等[9]通过将中间神经元转化为相应的连接路径,观察兴奋性刺激药物在删除不同连接路径时对肢体动物的运动步态的影响,得知运动频率由神经元兴奋和连合通路的参数所控制,删除不同类型的路径时,神经元网络也表现出不同的同步与交替现象,这一结果也与文献[10]相符。

本文通过对2个耦合的CPG神经网络引入刺激药物NMDA,这一药物具体表现为应用离子通道中的参数反转电位,通过控制NMDA的浓度观察肢体动物在不同连接路径的步态模式。数值仿真软件为XPPAUT,积分步长0.01,使用的四阶龙格库塔算法。

1 数学模型

本文研究的肢体动物左右肢协调步态运动的神经网络模型由文献[9]给出, 该模型由2个CPG构成,分别控制左、右肢的节律运动。每个CPG由相互抑制耦合的屈肌中心和伸肌中心组成。左、右CPG中心之间主要考虑3条路径:兴奋性V3中间神经元调节左屈肌、右屈肌中心的相互兴奋；抑制性V0D中间神经元调节2个中心相互抑制；兴奋性V0V中间神经元也参与这些中心的相互抑制,同时促进相互交替。该模型示意图如图1所示。

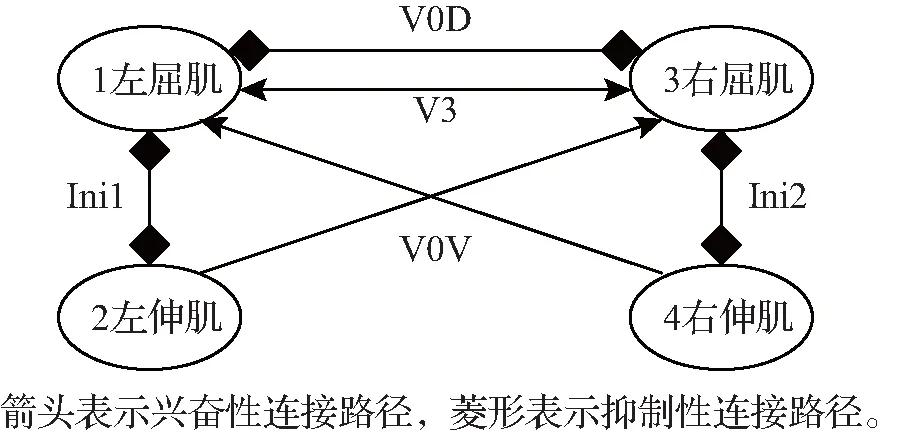
图1 简化模型示意图

外界驱动改变CPG神经网络的运动节律模式。外界驱动不仅对兴奋路径产生影响,同时对神经元的动力学行为产生影响，因此,本文在文献[9]的基础上对神经网络模型进行改进,得到的模型为

(1)

(2)

其中:

Inapi=gnapim∞(vi)hnap(vi-vna),Ili=gl(vi-vl),Iappi=gapp(vi-vapp),

式中:变量v、h、m分别为电压、钠、钾离子门通道打开的概率；i=1,2,3,4分别为各中心对应的指标；Cm,为膜电容,Inap、Iapp、Il、IsynE、IsynI分别为持续钠电流、应用电流、漏电流、兴奋性突触电流和抑制性突触电流；g代表相应的电导。突触电流如图1 所示,这里仅写出细胞1的突触电流,其他的类似。

IsynI1=[adf(v3)+b2f(v2)]gsynI(v1-vsynI),IsynE1=[a3f(v3)+avf(v4)]gsynE(v1-vsynE),

式中:vmin、vmax分别为达到阈值和饱和状态的电压；gsynE、gsynI分别为兴奋性和抑制性突触通道的最大电导；vsynE、vsynI分别是兴奋性和抑制性突触的反转电位；ad、av、a3、b1、b2分别为连接路径V0D、V0V、V3、Ini1、Ini2的突触权重；其中f(v)表示规范化输出电位,关于其他变量的描述在文献[9]中可找到。为体现细胞在外界药物刺激下运动节律模式发生的变化情况,在模型中引入参数α,并定义

vapp=vapp0(1-α)。

(3)

另外,为了更好地模拟刺激性药物对兴奋路径的影响,需要对这些连接进行突触加权,以增加参数α所代表的NMDA浓度,因此记a3=a30(1+β3α)，av=av0(1+βvα)。

2 动力学分析

2.1 单个神经元的动力学行为

此时只考虑单个细胞的运动节律,以左屈为例,在方程(1)中不需要再考虑突触电流,因此,这一情形的膜电位是由Inap、Il、Iapp三者所决定。单细胞模型在(v,h)相平面的周期轨和零值线如图2所示。图中v零值线(三次型)与h零值线(单调递减)的交点位于v零值线的中支,这也是系统的平衡点,并且是不稳定的,闭轨线是模型的一个稳定极限环,关于这类研究在文献[11-12]已有介绍。右侧为周期轨对应的膜电位波形图,周期T=1 283 ms,单位周期中的4个部分分别对应细胞在基准驱动上的静息状态、向上跳跃状态、活跃状态以及向下跳跃状态。根据神经元的运动状态,周期轨可分为4个部分:①静息状态；②向上跳跃状态；③激活状态；④向下跳跃状态。

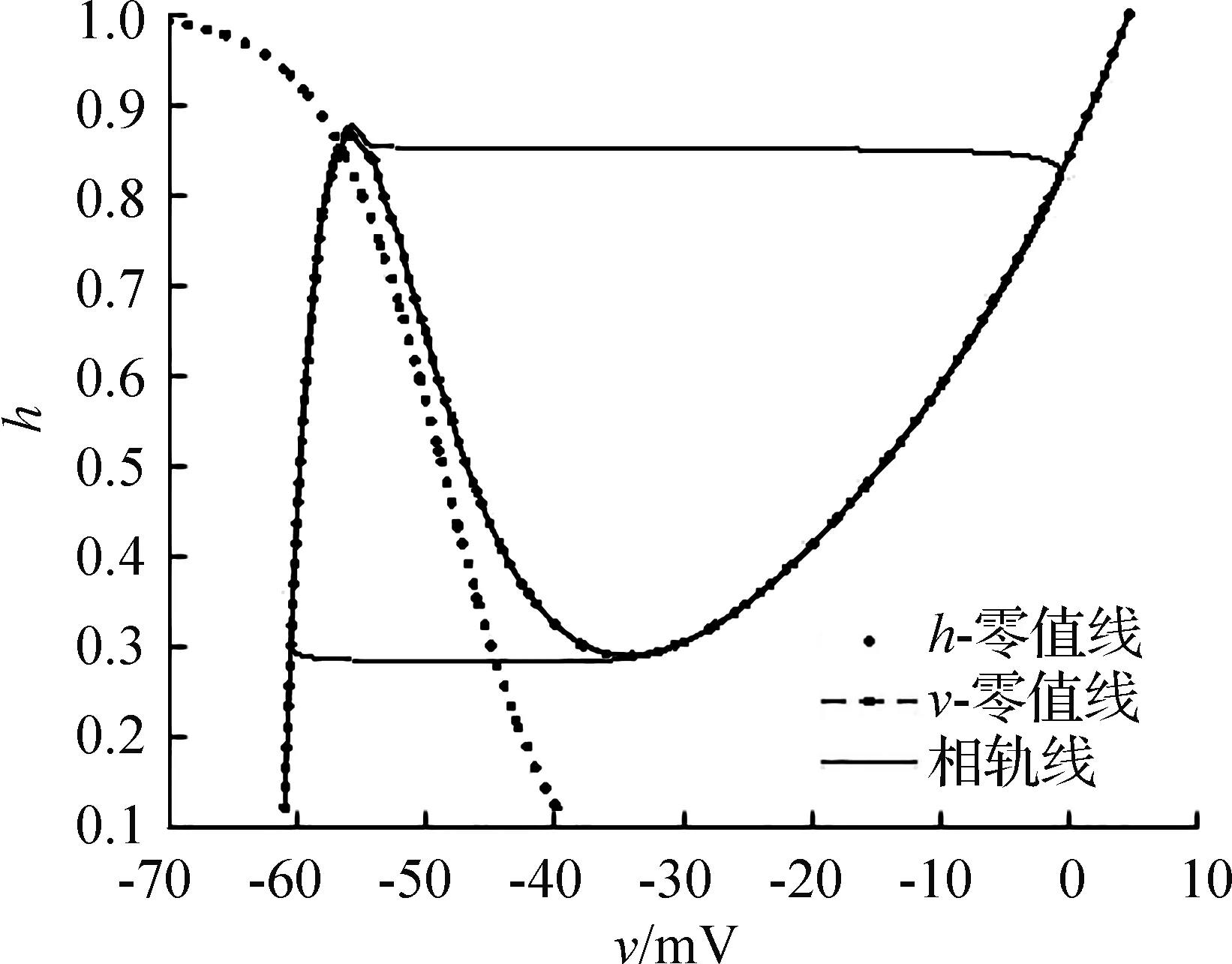
图2 单细胞模型在(v,h)相平面的周期轨与零值线

在静息和活跃状态,解曲线分别靠近v零值线的左、右分支；而向上、向下跳跃状态出现时在轨迹上到达左右拐点。由几何奇异摄动理论,向上、向下跳跃状态满足方程的快子系统,而静息和活跃状态对应慢子系统的解。细胞从①区出发,经过Ts时间后,到达左拐点处附近；在②区神经元向上跳跃,为瞬时活动；在③区,细胞逐渐活跃,经过Ta时间后到达④区；④区为向下跳跃状态也为瞬时活动,最终完成一个周期运动。

Iapp随时间的变化情况如图3所示。从图中可见,Iapp具有周期性,而构成这一项的主要参数是vapp与gapp,vapp的分岔图如图4所示。从图中可见,随着vapp的增加,平衡点从最初的稳定变为不稳定,在HB处稳定性发生改变,再次回到稳定状态,并从HB产生稳定的极限环,说明有一个Hopf 分岔出现,而且是超临界Hopf分岔。极限环由稳定变为不稳定,SN为周期轨上的鞍结点。本文主要研究的是神经元在周期轨的运动模式,故取vapp∈(-5.541,91.8)。由前所述,每个单一的神经元可处于以下3种状态:静息、振荡、强直。在该范围内,神经元是振荡的。再根据α与vapp的关系(图5),得出本文所考虑的α的范围为(0,2.8]。

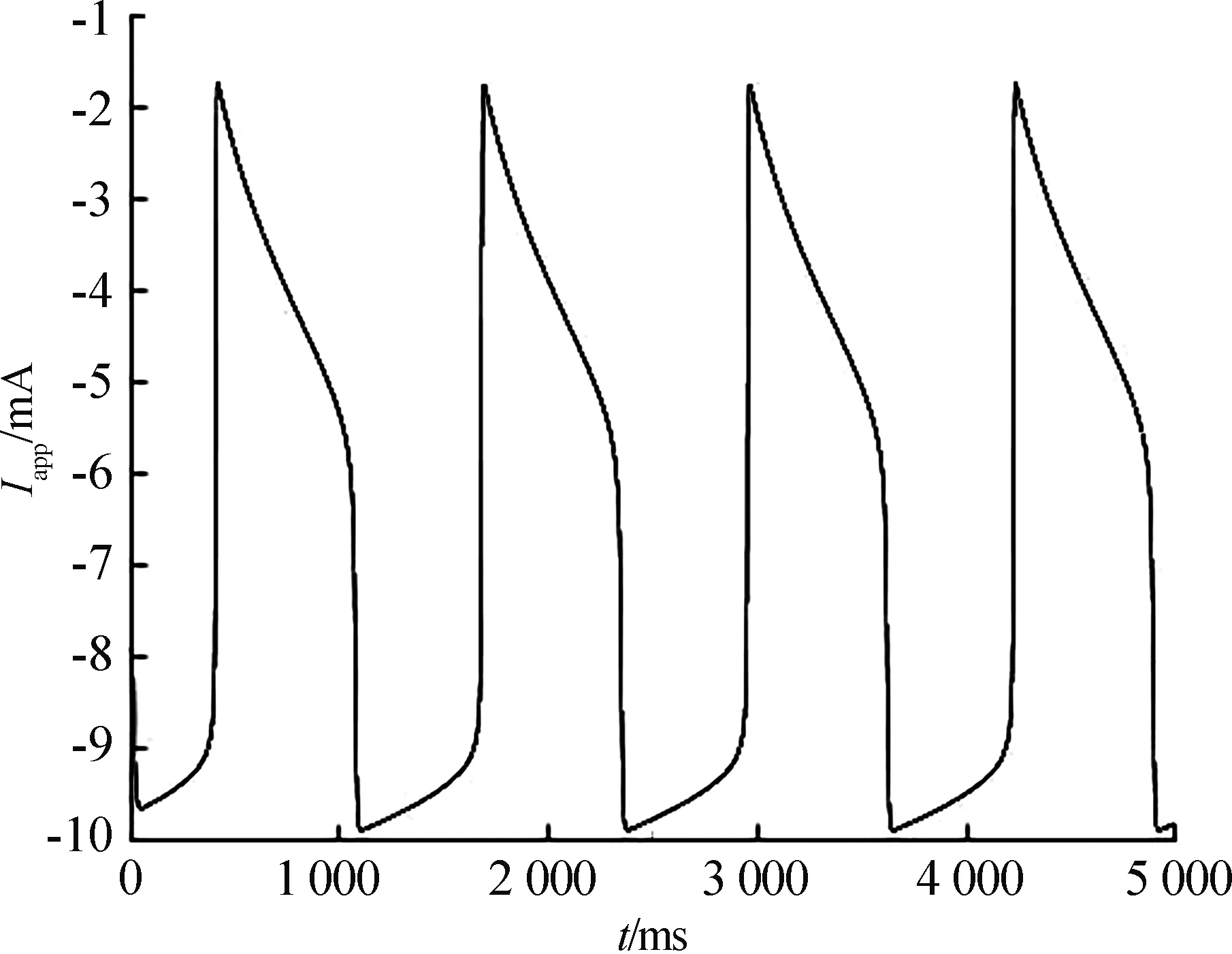
图3 Iapp随时间的变化情况

图4 单神经元模型关于参数vapp的分岔图

图5 外界参数α与vapp的关系

2.2 完整神经网络模型的动力学行为

现在讨论完整的神经元网络模型,本文的完整模型是由2个CPG耦合的神经网络构成,经过突触连接,构成一个8维的非线性微分方程组。首先通过相平面分析,分析4个神经元的动力学行为。

4个中心的零值线、周期轨与动作电位,如图6所示。由图中可见,左右中心的周期轨和动作电位具备相同的特征。CPG在受外界刺激情况下,尽管左右中心的电位振幅有所不同,但相位差保持一致,这就是相位同步,表现为图7中的相位差恒为0。而同侧中心运动模式较为复杂,左侧中心在受外界刺激时运动初期不太稳定,在静息状态存在小范围的扰动,但扰动会随着时间而消失,后面将说明这种扰动也会随着NMDA浓度的增加而消失。由于2个CPG具有相同的特性,因此只需讨论其中一个在外界刺激下的运动,现着重比较左侧中心的变化。

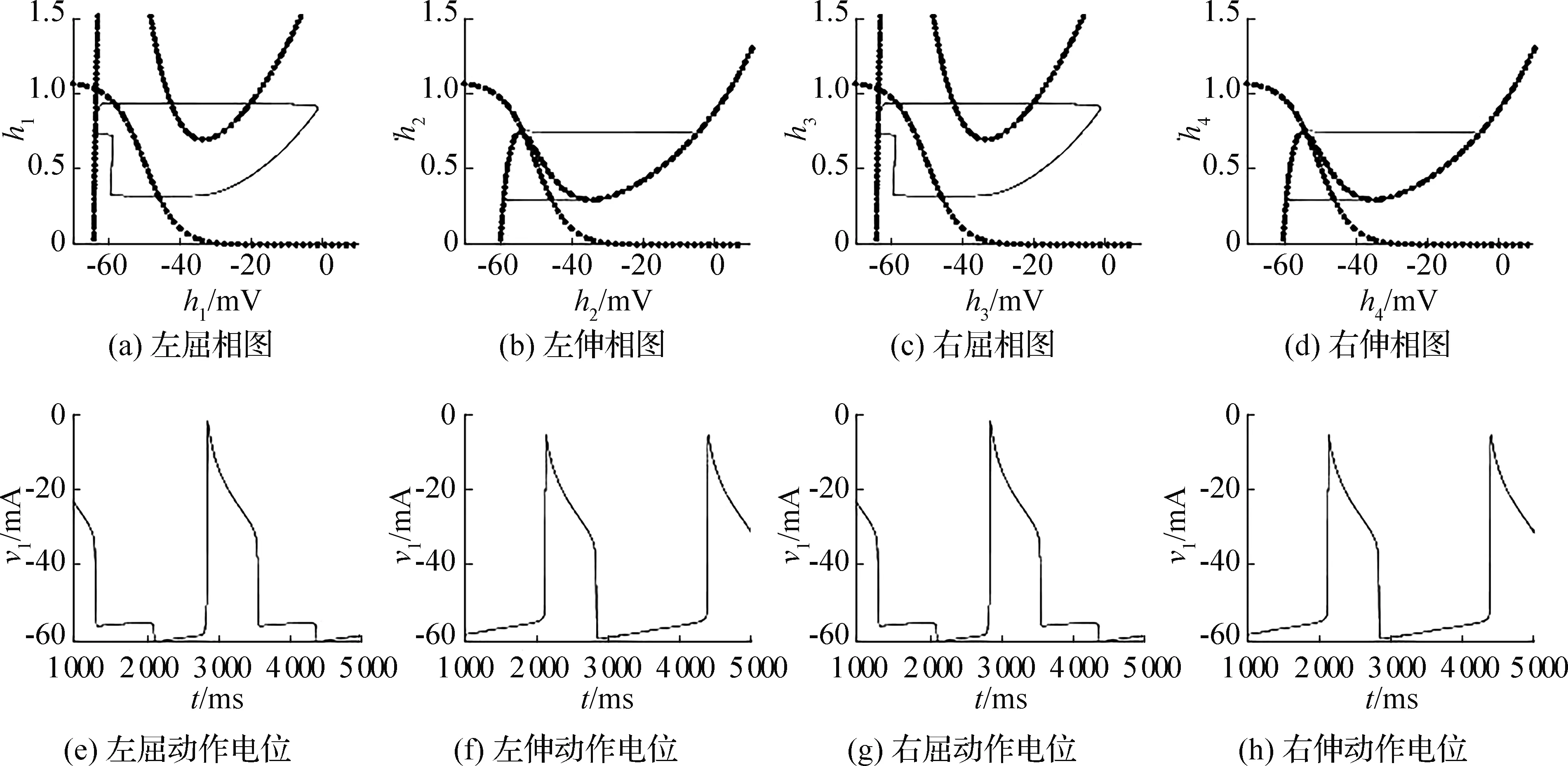
图6 4个中心的零值线,周期轨与动作电位

图7 中心相位差

左侧中心在α=0.1,α=1.0,α=2.8时的零值线、周期轨与动作电位,如图8所示。随着α增加,左屈肌与右屈肌始终是完全同步的,而左侧中心在一定时刻以后对不同的参数都始终趋向一个非零数,说明在完整模型中左侧中心在不同外界刺激下受α的影响比较大,其相位差的幅度逐渐减少,而且由对称逐渐转化为非对称。屈肌与伸肌中心的周期轨和动作电位具备相同的特征,即细胞1与细胞3,细胞2与细胞4两组中心的具有对称性。从图1中就能看出,这也是文献[1、13]所研究的基于持续性钠电流的半中心振荡。

同侧中心有许多共同点,h是与通道门有关的状态变量,外界药物不会影响各离子通道打开的概率,另外,在与h有关的方程中不显含α,无论α取何值,都不会影响到h零值线。相比之下,2个中心的v零值线受α的影响比较大,都是随着α的增加,其左膝值的h轴坐标下降,平衡点与左膝值的变化相同,不管α在所给定的区间上如何变动,各中心的零值线始终保持三部分。并由此确定了α的区间,在图8中,细胞1与细胞2对α取不同值都始终存在闭轨,这与图4中参数vapp的分岔的情况相符。其次,随着α增加,周期变小,意味着在外界药物的刺激下,细胞活动变得更加兴奋,这与右栏周期放电的频率增加相符,且尖峰电位也随之下降。

同侧的电位活动也存在着较大差异,前者在α=0.1,α=1.0处的平衡点位于零值线的左支,在α=2.8处位于中支,说明细胞1在外界药物刺激的作用下,显示处于兴奋状态,在药物达到一定剂量后开始变为振荡,而细胞2始终是处于振荡状态,而不受外界药物的影响,此外,细胞1在刚接触到外界刺激时静息状态表现出很大差异,在这活动期间还出现了一个短暂的向上跳跃状态,称为阈下放电,为了更好表现二者在周期轨与尖峰电位受α影响程度的差异,将区间细分,取步长0.3,同侧中心的规范化周期与尖峰电位如图9所示。

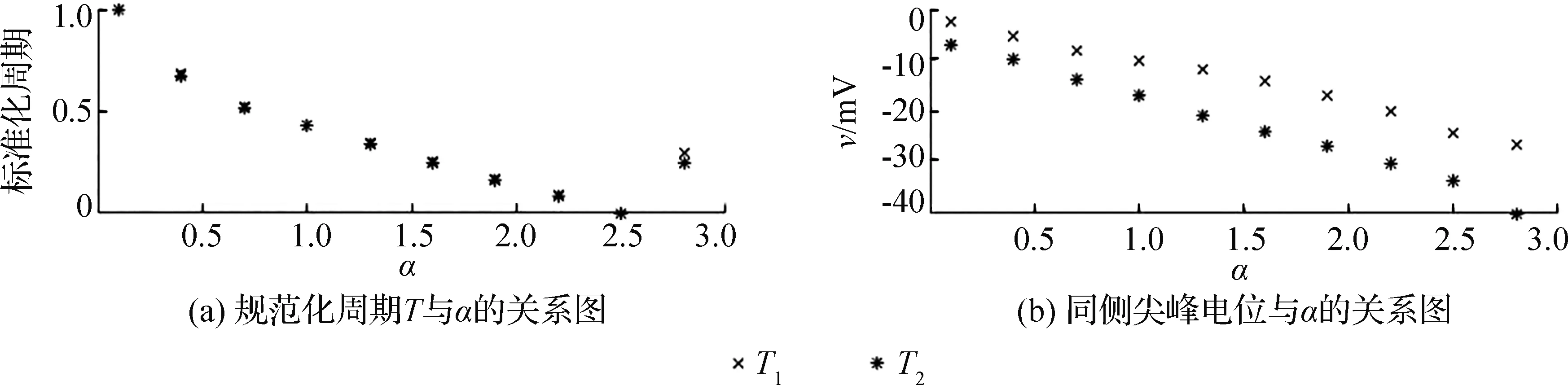
图9 同侧中心的规范化周期与尖峰电位

前面已经说明左右中心是同步的,而同侧是交替的,从图8(a)、8(c)可以看出作图的周期几乎一致,仅仅是在α=2.8处稍有不同,确切的说是这一点处的细胞活动反常,在此之前,同侧中心的活动周期与动作电位都是随着α单调下降,而在这点却增加,这是因为,当外界药物达到一定剂量之后,细胞的反应不再像之前那样强烈,而是逐渐到达一种平衡状态,其相轨线具体表现为靠近平衡点,而在α=2.8时已经逐渐接近这种临界状态,此前的2个周期已经变为1个次周期,这就是周期2峰放电。换言之,将观察到的实际周期除以2依旧满足之前单调下降的特征。图8(c)、8(d)中细胞在该点处的动作电位也符合这一特征。

2.3 删除V0D

在完整的耦合模型中主要考虑了V3中间神经元、抑制性V0D中间神经元与兴奋性V0V中间神经元,而外界刺激药物主要是影响了细胞的兴奋性程度,路径V0D的权重并不与α直接相关,因此,此处考虑删除路径V0D以后细胞随α的变化情况。构成Iapp电流的还有基准应用逆转势电位,删除V0D路径之后,这一参数也可能会影响模型的稳定性,对该参数进行分岔分析与图4基本相同,依旧存在超临界的Hopf分岔,其中分岔点为vapp0=168。在这一模型中仍取vapp0=-50。在删除V0D后,周期轨上的鞍结分岔点消失。

删除路径V0D的模型下周期轨及动作电位,如图10所示。各细胞的活动情况与完整模型中的并无很大差异,周期轨与零值线的位置也几乎一致,放电周期与尖峰电位也没有太大改变。可以说这一情形下的各细胞的运动节律模式与完整模型几乎一致,完全符合这条路径的属性,路径V0D是由抑制性V0D中间神经元改变得到的,而抑制性神经元与外界刺激药物非直接相关,所引入的参数α无法影响这条路径,故关于这条路径V0D的周期变化情况与前者类似。屈肌与伸肌中心仍然是完全同步。在完整模型中,同侧中心在一定时刻后的相位差逐渐趋于一个固定值,而且随着参数的改变这一固定值也会减小,而在删除V0D模型下同侧中心的相位差不再稳定在某一固定值,而是沿着v=0周期性的波动,当参数增加到临界值时,变化幅度变小,而此时的振幅并无关联,说明同侧中心随着参数的逐渐增加开始出现同步现象。

图10 删除路径V0D的模型下周期轨及动作电位

2.4 删除V0V

前面已经讨论了删除与外界刺激无关的路径V0D的情况,剩下的2条兴奋性路径V3、兴奋性V0V均与外界药物刺激直接相关,现讨论删除路径V0V的情形。

左侧屈肌与左侧伸肌中心对所考虑的α是交替的,但交替周期随着α的增加而减少,使运动频率增加。这点在动作电位与输出函数上表现出较大的相关性,因为所定义的输出函数就是对电压的规范化。最大的差别表现在向下跳跃状态,左屈中心受到外界刺激时在向下跳跃的过程中出现较长的阈下电位,而这一状态随着时间的增加持续时间越来越短,直至消失,当外界药物增加到一定程度后,又重新开始出现新的放电,此时的放电不同于前者,从输出函数图上表现为周期2峰放电。

屈肌与伸肌中心始终表现为完全同步(图11)。而左屈与左伸的相位差与其动作电位间的变化情况几乎相同,尤其是在向下跳跃状态依旧表现出阈下放电,这一行为在相位差的图中渐趋于0,说明左屈与左伸在交替中仍有出现相位同步,只不过随着α的增加,相位同步逐渐消失。

图11 反相同步与完全同步

3 结论

不同的外界刺激可以引起放电节律模式发生改变,也会导致神经元产生不同的生理效应,刺激幅度偏离需求值以及周期偏大或偏小都无法对疾病产生好的效果,甚至会加重病情[14]，因此,了解不同的节律模式与外界刺激之间的关系将有助于解释外界刺激导致的疾病所产生的机理,在临床治疗时,刺激的相关参数控制在合理的范围内显得尤为重要。本文考虑了一个基于持续性钠电流和应用电流的2个CPG耦合的神经网络模型,研究了外界刺激药物NMDA对运动步态节律的影响。首先对应用反转电位vapp作分岔分析,由此确定外界参数α的范围,本文章后面部分都是基于这一范围对模型进行分析。通过研究完整网络中各细胞的放电活动发现左右中心是同步的,而且这一现象不会受到NMDA浓度变化的影响,同侧中心则表现为交替活动,但这种交替行为容易受到外界药物的干扰,在交替与同步中相互转化。接着又分别讨论了删除抑制性路径V0D和交替兴奋性路径V0V的模型,并相互比较,观察到左右中心在这2种情形下都表现出与完整模型相同的特征,即神经元始终是同步放电,不受外界刺激的影响,周期的变化情况也大致相同,主要的差别是在同侧中心,动作电位及相位差都随着参数的变化而变化,本文也是将重点放在了这一部分讨论,这一结论符合文献[15]中关于复杂网络鲁棒性的研究。关于具体的实验数据见文献[6],实验分别在野生型和转基因去雄小鼠脊髓中进行。关于多个CPG耦合的运动机制是如何整合起来产生稳定肢体间的相互作用,这在很大程度上仍是一个未知的领域,仍将是一个活跃的研究领域。