高地下水位冻土区弧形底浅拱梯形渠道冻胀力学分析

肖旻，熊志豪，吴浪*，崔浩，杨晓松，葛建锐

高地下水位冻土区弧形底浅拱梯形渠道冻胀力学分析

肖旻1，熊志豪1，吴浪1*，崔浩1，杨晓松2，葛建锐3

（1.江西科技师范大学 建筑工程学院，南昌 330013；2.塔里木大学 水利与建筑工程学院，新疆 阿拉尔 843300；3.兰州理工大学 能源与动力工程学院，兰州 730000）

【目的】明确高地下水位冻土区弧形底浅拱梯形渠道冻胀破坏机理并提出简捷、实用的抗冻胀设计方法。【方法】考虑此类渠道拱高明显小于断面整体深度的特殊性，基于Winkler假设提出衬砌体法向冻胀力计算方法。论证高地下水位渠道衬砌体微小刚性上抬位移对曲线形弧段切向冻结力的影响机制并提出切向冻结力计算方法。基于此构建高地下水位冻土区弧形底梯形渠道冻胀力学模型。【结果】以某弧形底梯形渠道为原型，对比分析不同渠底中心地下水位对衬砌板截面内力及所受冻胀力的影响。结果表明，越小则截面内力及冻胀力分布的横向差异越明显；0越大，截面内力及冻胀力分布受地下水补给条件的影响越小，与事实相符。充足的水分补给时间、补给来源以及冻胀力横向的不均匀、不同步是此类渠道易遭受冻胀破坏的主要原因。【结论】该模型可较好地反映此类渠道的冻胀受力特性，计算结果合理、可靠，可为高地下水位冻土区弧形底浅拱梯形渠道抗冻设计和相关研究提供参考。

冻土工程；灌溉渠道；力学模型；弧底梯形；高地下水位

0 引言

【研究意义】渠道渗漏是农田灌溉中水分损耗的主要原因之一，混凝土衬砌是减少水分渗漏、提高水资源利用效率的有效方法。然而，在我国北方干旱寒冷地区，渠道经常遭受严重冻害[1-2]。高地下水位渠道尤其如此。这类渠道在山区和平原较多见，如新疆塔里木灌区、甘肃白银引黄灌区下游以及河西走廊内陆河流域中下游地区均有大量修建[3-5]。高地下水位渠道往往成为冻土区渠系工程的难工地段与瓶颈渠段，需要更多地加以关注。【研究进展】近年来，众多学者对渠道冻害机理及冻胀力学模型进行了研究[6-8]。王正中等[9]、肖旻等[10]对现浇混凝土衬砌梯形渠道，申向东等[11]、肖旻等[12]对预制混凝土衬砌梯形渠道，宋玲等[13]对冬季输水工况下的梯形渠道，唐少容等[14]对三拼式小U形渠道，葛建锐等[15]对冰盖输水工况下的梯形渠道分别建立了冻胀力学模型。安鹏等[16]结合有限元方法建立了弧底梯形渠道抗冻胀结构优化模型。李宏波等[17]提出了一种结合力学模型基于实测冻胀变形反演渠道冻胀内力的解析方法。刘东等[18]结合冻胀力学模型基于PSO算法进行梯形渠道断面的优化及参数分析。由此可见，关于渠道冻胀力学模型的建立与应用方面已有大量探索。【切入点】弧底梯形渠道因其具有良好的适应冻胀能力而得到广泛推广应用，但在广大季节性冻土区尤其是高地下水位地区仍极易发生冻胀破坏。建立简捷、实用的高地下水位冻土区弧底梯形渠道冻胀力学模型很有必要。此外，已有模型中对弧底板切向冻结力分布的假定也缺少必要的论证。【拟解决的关键问题】为此，本文以高地下水位冻土区弧形底浅拱梯形渠道为研究对象，分析其冻胀特征，进而构建冻胀力学模型。

1 模型的建立

1.1 高地下水位冻土区弧形底梯形渠道冻胀特征

高地下水位渠道基土冻结过程中存在明显水分补给，易引发显著冻胀变形。此时冻土-衬砌间法向冻结约束有时不能阻止基土冻胀引起的衬砌结构整体上抬趋势。由于弧形底梯形渠道良好的整体性和复位能力，法向约束失效并不意味着结构最终破坏，还需要进一步的验算和校核。鉴于此，本文考虑无法向冻结约束的情形，对高地下水位区微小刚性上抬的弧形底浅拱梯形渠道进行力学分析。现对其工程特性与冻胀特征作简要分析：

1）特定地区具体气象、土质条件下，地下水迁移与补给是影响高地下水位地区渠道断面各位点基土冻胀强度的主要因素[3-4, 19-20]。

2）弧形底梯形渠道断面连续光滑、无板间接缝与拐角，其整体性显著强于普通梯形渠道。因此，冻胀力作用下衬砌结构有整体上抬趋势。又由于太阳辐射差异造成阴、阳坡受力不均衡，易使结构发生微小刚性转动。通过这种位移协调与变形释放将使结构二侧受力趋于均匀分布[3, 21-23]。基于此，本文中采用对称模型。

3）衬砌板所受法向冻胀力、切向冻结力分布规律除受各点至地下水埋深距离不同的影响外，曲线段底板还受到各点局部几何特性影响。由于浅拱梯形渠道拱高相比断面深度小很多，从而不考虑地下水分补给差异对弧底板各点受力变形的影响，认为法向冻胀力均匀分布，切向冻结力则仅受到弧底板各点局部几何特性的影响。

1.2 基本假设与计算简图

结合已有研究与工程实践[3-4, 9-15]，做如下假设：

1）渠道沿输水方向尺寸远小于横向尺寸，渠道的冻胀力学分析简化为平面应变问题。

2）冬季漫长，渠道基土冻结速率缓慢，结构冻胀破坏视为准静态过程。即基土冻结冻胀过程中结构始终处于平衡状态，当发生冻胀破坏时则处于极限平衡状态。

3）渠基土满足Winkler假设中的局部性要求[24-25]，即衬砌各点所受冻胀力大小仅由各点对应处渠基土局部的冻胀特征决定[3-4, 26-27]。对特定气象、土质条件下的高地下水位冻土区渠道而言，衬砌各点对应处基土冻胀强度由各点地下水位决定[3-4, 19-20, 26-27]。

4）浅拱渠道拱高较小，从而各点至地下水埋深（即渠顶地下水位）的距离相差不大，故可认为弧形底各点所受法向冻胀力近似均匀分布。

图1为弧形底浅拱梯形渠道断面示意图。m、s为两侧坡顶；2为开口宽度（m）；2为弧形底的圆心角（rad）；为断面深度（m）；为拱高（m）；为弧底半径（m）；=为坡角（rad）；为渠底中心处地下水位（m）。()为作用在衬砌板上的法向冻胀力（Pa）；()为作用在衬砌板底部的切向冻结力（Pa）；0为弧底板所受法向冻胀力（Pa）；max为衬砌直线段与曲线段连接处切向冻结力（Pa）。C点为衬砌体直线段与曲线段的连接点。渠顶地下水位为0（m），显然有0=+。

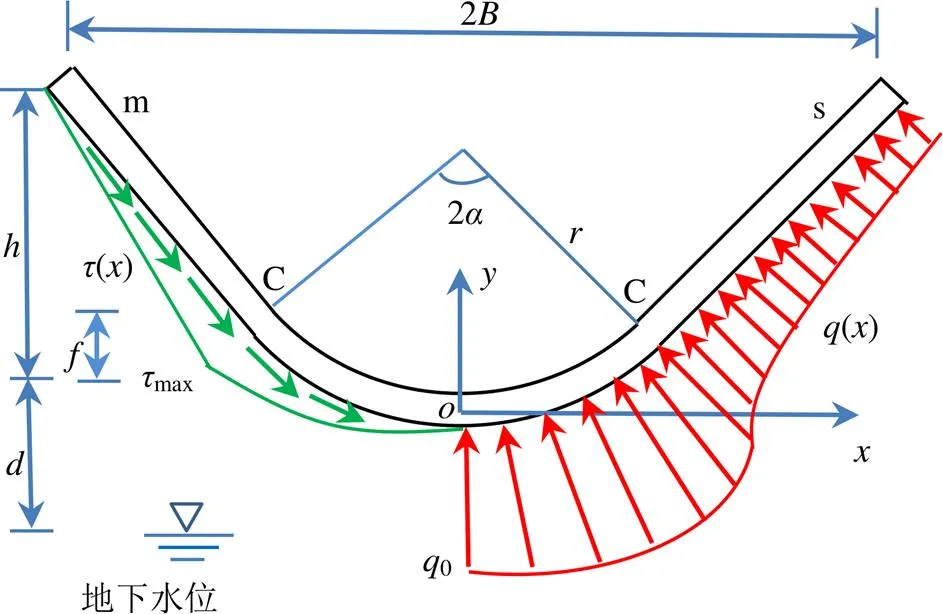
图1 弧底梯形渠道断面示意

1.3 法向冻胀力

采用图1所示坐标系，弧底梯形渠道断面曲线方程如下（考虑到对称性，仅给出侧表达式，下同）：

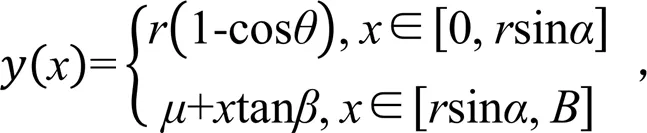
式中：为断面曲线各点切线与轴正方向的夹角（rad）；=-·sinα·tan；拱高为=(1-cos)。

由几何关系，衬砌各点地下水位为：()=+()。

大量研究表明[2-4, 12, 15, 19-21, 26-30]，冻土冻胀率与地下水位之有如下函数关系：

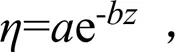
式中：为冻土冻胀率（%）；为计算点地下水位（m）；、为与特定地区气象、土质条件有关的经验系数，反映了除地下水补给以外其他影响因素的综合影响，可结合试验数据拟合获取。考虑到衬砌各点地下水位不同，应用Winkler模型中的局部性假设，即认为衬砌体某处法向冻胀力大小仅与该处局部基土冻胀特征有关，结合木下诚一冻胀力与冻胀率的线性关系[20-21, 26-27, 30]，可得衬砌各点法向冻胀力分布：

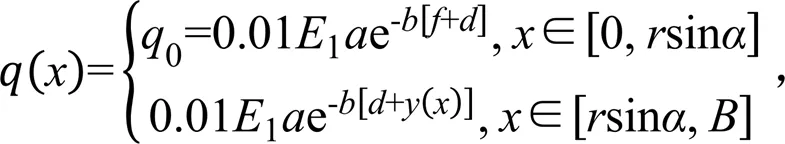
式中：1为冻土弹性模量（MPa）。令()=tan，则()沿轴方向分量为q()=()[/(1+2)1/2]，其沿轴方向分量为q()=()[1/(1+2)1/2]。

1.4 切向冻结力

此处切向冻结力是指因衬砌体的微小刚性上抬使冻土与结构接触面有相对位移趋势时在衬砌底面引起的冻结摩擦阻力。

就特定地区高地下水位衬砌渠道而言，直线段坡板主要考虑各点地下水补给条件的差异确定切向冻结力分布，即()越小的位点切向冻结力就越大，自坡顶沿坡面线性增大，到直线段与曲线段的连接处取最大值；对曲线段弧底板，因浅拱渠道弧底板各点地下水位相差不大，从而应主要考虑断面几何特性的影响。如图2所示，设想弧底板各点产生相同的微小刚性上抬位移Δ，不同的各点投影到接触面上的相对位移不同，其他影响因素相似时，将引起各点切向冻结力大小不同。当越大投影到接触面上的相对位移Δ=Δsin就越大，则切向冻结力也越大。同时考虑到对称性，弧底中心处切向冻结力应为0。基于以上分析，基于切向的Winkler假设[31]，现补充如下假定：弧底板各点切向冻结力大小与接触界面切向相对位移Δ成正比即与sin成正比。综上，切向冻结力大小可由下式计算：

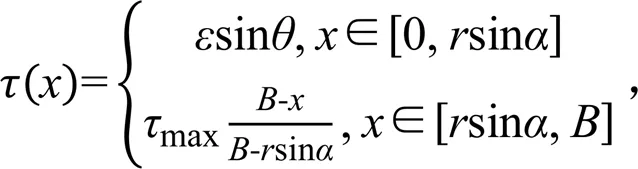
式中：ε为比例系数。可见上式能满足渠底中心切向冻结力为0的必要条件。事实上，这可以看作接触面切向相对位移Δv为0时的特殊情形。类似地，切向冻结力在x轴方向的投影为τx(x)=τ(x)[1/(1+m2)1/2]；在y轴方向的投影为τy(x)=τ(x)[m/(1+m2)1/2]。

2 模型的求解

2.1 切向冻结力计算

求解()的关键在确定比例系数。因衬砌体为薄板结构，故不考虑重力影响，是偏安全的。依据侧衬砌板竖直方向静力平衡条件，有下式成立：

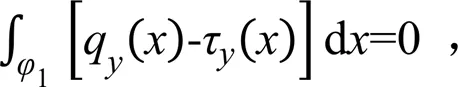
式中：1为衬砌结构的s侧部分，包括直线段及弧形底的1/2；d为弧微分。把式（3）、式（4）代入式（5）并积分可得：

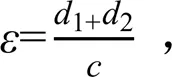
其中，

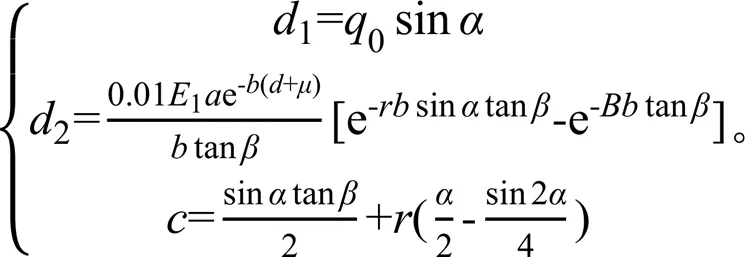
对于特定的具体渠道而言，式（7）中的相关参数均为已知，从而由式（6）即可确定系数，进一步可确定切向冻结力的分布规律。

2.2 截面内力计算

仍以s侧为例。取横坐标为´的截面（称截面´）及该截面以上部分为隔离体。

1）直线段

首先计算衬砌体直线段各截面轴力(´)、剪力(´)与弯矩(´)。其中(´)由下式计算：

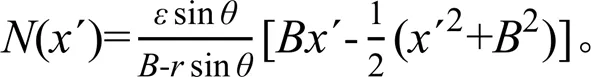
(´)由下式计算：

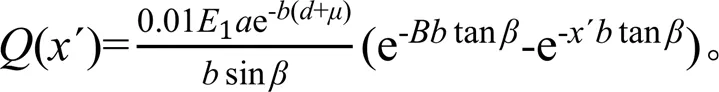
(´)由下式计算（以内侧即底面受拉为正）：

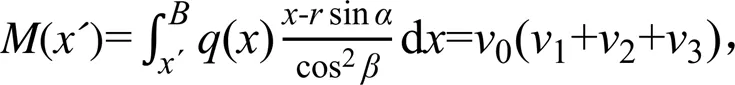
其中，

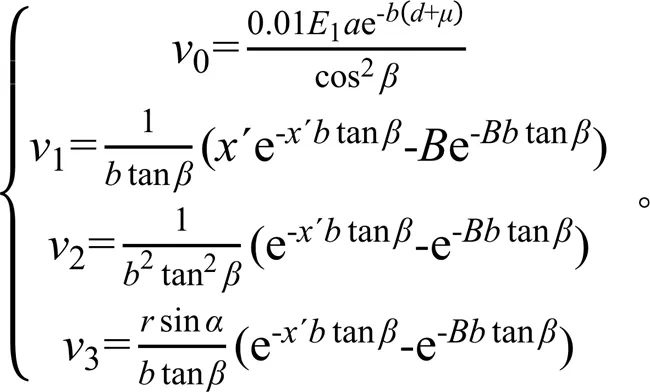
由式（8）—式（10）可确定直线段与曲线段连接处C点的轴力c、剪力c及弯矩c。

2）曲线段

截面合力是截面轴力与截面剪力的合力。确定截面合力后可通过投影获得各截面轴力与剪力。现计算衬砌体弧形底各点截面合力N(´)。N(´)在轴方向的分量N(´)可由下式计算（投影到切线方向后是拉力为正）：

N(´)在轴方向的分量N(´)可由下式计算：

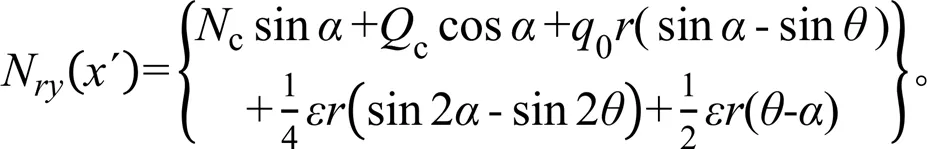
结合式（12）、式（13）可得截面合力N(´)如下（其方向可由上述2个投影分量的计算结果确定）：

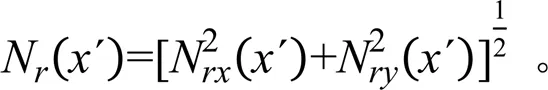
由力矩平衡条件可得弯矩(´)的计算式为：

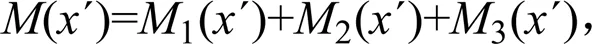
式中：1(´)为衬砌体直线段与曲线段连接处截面内力在截面´处引起的弯矩；2(´)为法向冻胀力()在截面´处引起的弯矩；3(´)为切向冻结力()在截面´处引起的弯矩。各截面内力确定后，参照已有研究[7]，由工程力学方法可进行抗冻设计，对衬砌体强度进行校核，并对易裂位置是否安全进行验算。

3 工程算例

以某弧形底浅拱梯形渠道为例。该地区干旱少雨、寒冷多风，有河流穿行且建有平原水库，地表水丰沛。地下水为河流两岸嵌入式淡水体，地下水埋深浅。对于此类高地下水位寒旱区，引发基土冻胀的主要水分来源为地下水，地下水补给条件是决定衬砌各点对应处基土冻胀强度的主导因素。该渠道为C15混凝土衬砌，板厚为0.15 m。弧形底半径为1.2 m，坡角为30°，直线段板长为3 m。渠基土土质为壤土，极端最低气温可达-29 ℃，冻土层最低温度约为-15 ℃。基土冻深约1 m。表1所示相关参数与经验系数按冻土层最低温度取值，这是偏安全的。弧形底板拱高约占渠道断面深度的1/10，故该渠道属于弧形底浅拱渠道。

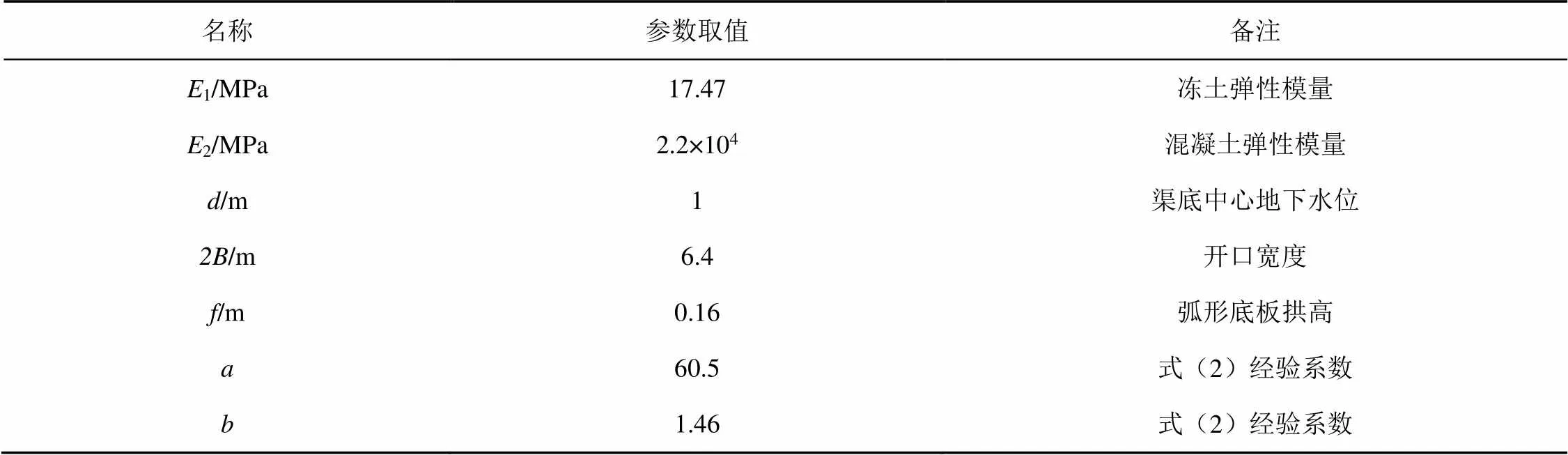
表1 相关参数与经验系数[20,28,32-33]

1）截面内力

首先应先确定切向约束反力()的分布规律，关键在于确定系数。对本例中特定地区具体衬砌渠道而言，相关参数以及经验系数均是确定的，代入式（6）、式（7）中可得=15.18。基于此，通过式（8）、式（10）可得衬砌体直线段截面轴力及弯矩分布。取弧形底板中心处地下水位分别为0.5、1（真实值）、1.5、2 m时进行计算，分析高地下水位冻土区地下水位对衬砌体截面内力及冻胀力分布的影响，计算结果如图3所示。

由图3（a）可见，就衬砌体直线段而言，截面轴力自渠顶沿坡面向直线段与弧底板的连接处（即C点处）逐渐增大，在C点处达到最大值，且均为压力，变化趋势与已有研究相符[22]。对不同渠底中心地下水位时的结果进行对比分析表明，渠底中心地下水位对远离C点处的截面轴力影响较小；当临近C点时，同一位置随增大，截面轴力迅速增大。

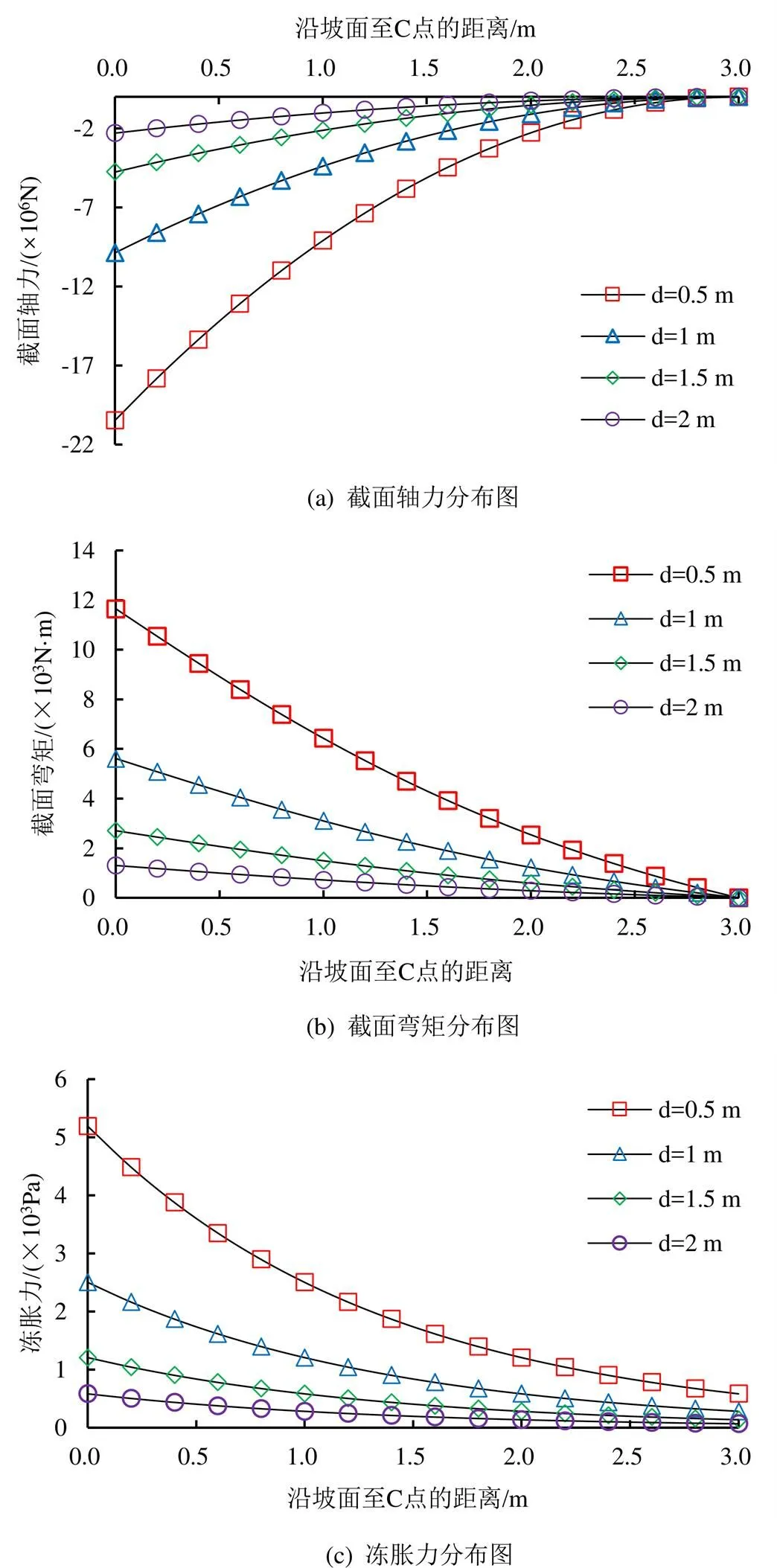
图3 衬砌体直线段内力与冻胀力分布图

由图3（b）可见，衬砌体直线段各截面弯矩自渠顶沿坡面向C处也逐渐增大，在C点处达到最大值，这也与已有研究相符[22]。对比分析结果表明，对截面弯矩的总体变化趋势影响较小，但对截面弯矩大小尤其是对最大弯矩影响显著。由式（10）可知，对于特定断面的弧形底梯形渠道而言，随着越小，最大截面弯矩将呈指数规律增大，这表明高地下水位冻土区渠道衬砌极易因局部弯矩过大而遭受冻胀破坏，这与事实相符。

如图3（c）是不同时冻胀力沿坡板分布规律。由图3（c）可见，冻胀力分布呈明显的横向差异即不均匀性，且越小即0越小时，这种横向差异越显著；0越大时，冻胀力量值迅速减小且横向差异逐渐减弱，表明地下水补给的影响随着0增大而迅速变小，这与事实相符。对于固定的特定渠道而言，冻胀力自坡顶向C点处呈指数规律增大，越靠近地下水位，冻胀力越大且分布越不均匀，越远离地下水位，冻胀力则越小且分布越均匀。

2）易裂位置与抗裂验算

结合工程实践、已有研究[22]及本文模型结果，最易破坏位置在衬砌直线段与弧底板连接处即C点与渠底中心附近。现以C点为例作抗裂验算。结合C点截面轴力及弯矩计算结果，得该处最大拉应力为：maxc=(6c/´2)-(c/´)=1.433 MPa≥[]=1.1 MPa，其中´为板厚（m）；[]表示允许拉应力（MPa）。

由此可见，C点处截面最大拉应力大于允许拉应力，表明由于受到高地下水位的影响，该渠道衬砌有开裂的可能。对于高地下水位渠道而言，充足的水分补给时间、补给来源以及法向冻胀力横向的不均匀、不同步是引起衬砌结构冻胀破坏的主要原因。

4 讨论

已有研究中[21]弧底梯形渠道直线段法向冻胀力常假设为线性分布，本文模型结合工程实践、试验研究[20]、木下诚一公式[20]及Winkler局部性假设[24-25]，提出直线段法向冻胀力的非线性分布规律，更加符合高地下水位冻土区的实际情况。此外，已有研究对弧形底所受切向冻结力分布的假定缺乏必要的论证，本文模型同时考虑地下水补给条件及弧底各点局部几何特性的不同，结合冻土-衬砌接触面切向相互作用特点，提出切向冻结力分布的非线性分布规律。结合工程实例进行分析，结果表明，该模型可以较好地反映高地下水位冻土区地下水补给条件对渠道衬砌体冻胀受力及冻胀变形的影响，估算的易开裂部位与工程实际及已有研究结果基本相符。

本文研究对象为高地下水位冻土区弧底浅拱梯形渠道，一般认为整个断面均处于地下水补给影响范围内，暂不考虑0大于临界值的情形。但实际上，对0处于临界值附近的过渡情形，该模型仍能较好地进行描述。工程实际中[26]，()越小的部位冻胀力量值较大且分布不均匀，()越大冻胀力量值较小且趋于均匀分布。本文中用于描述冻胀率、冻胀力的负指数函数关系恰好也具有类似特征，因此能较好地体现高地下水位及临界埋深附近的情形。

需要说明的是，本文模型未考虑因衬砌体微小刚性上抬位移引起冻胀力的消减和释放效应，这是偏安全的；此外，在渠坡顶部设置顶盖板的情形本文也未加以考虑。以上均有待进一步的深入研究。

5 结论

1）以高地下水位冻土区弧底浅拱梯形渠道为研究对象，分析此类渠道的冻胀特征，并构建相应冻胀破坏力学模型。针对此类渠道弧形底拱高相对整个断面深度较小的特点，采用弧底板法向冻胀力均匀分布的假设；同样基于此，指出当衬砌体产生微小刚性上抬时，弧形底板各点局部几何特性将对切向冻结力产生显著影响，并据此导出了一种曲线形弧段切向冻结力的计算方法。

2）以某弧底浅拱梯形渠道为例，对比分析了不同渠底中心地下水位对截面内力及冻胀力分布的影响。结果表明，越小则截面内力及冻胀力分布的横向差异越明显；0越大截面内力及冻胀力分布受地下水补给条件的影响越小，与事实相符。

[1] 王正中, 江浩源, 王羿, 等. 旱寒区输水渠道防渗抗冻胀研究进展与前沿[J]. 农业工程学报, 2020, 36(22): 120-132.

WANG Zhengzhong, JIANG Haoyuan, WANG Yi, et al. Research progresses and frontiers in anti-seepage and anti-frost heave of canals in cold-arid regions[J]. Transactions of the Chinese Society of Agricultural Engineering 2020, 36(22): 120-132.

[2] 何鹏飞, 马巍. 我国寒区输水工程研究进展与展望[J]. 冰川冻土, 2020, 42(2): 182-194.

HE Pengfei, MA Wei. Study of canals in cold regions of China: achievements and prospects[J]. Journal of Glaciology and Geocryology, 2020, 42(2): 182-194.

[3] 肖旻. 开放系统混凝土衬砌输水渠道冻胀破坏力学模型及应用[D]. 杨凌: 西北农林科技大学, 2018.

XIAO Min. Mechanical model and its application of frost heave damage of concrete lining canal under open system conditions[D]. Yangling: Northwest A&F University, 2018.

[4] 肖旻, 王正中, 刘铨鸿, 等. 考虑地下水位影响的现浇混凝土梯形渠道冻胀破坏力学分析[J]. 农业工程学报, 2017, 33(1): 91-97.

XIAO Min, WANG Zhengzhong, LIU Quanhong, et al. Mechanical analysis on frost heave damage of cast-in-place concrete trapezoidal canal considering influence of groundwater table[J]. Transactions of the Chinese Society of Agricultural Engineering 2017, 33(1): 91-97.

[5] 塔里木灌区水利管理处史志编撰委员会. 塔里木灌区水利管理处志[M]. 乌鲁木齐: 新疆人民出版社, 2001.

Compilation committee for the annals of water management department of Tarim irrigation area. The annals of water management department of Tarim irrigation area[M]. Urumchi: Xinjiang Peoples’ publishing house, 2001.

[6] 陈涛, 王正中, 张爱军. 大U形渠道冻胀机理试验研究[J]. 灌溉排水学报, 2006, 25(2): 8-11.

CHEN Tao, WANG Zhengzhong, ZHANG Aijun. The test for frost heaving damage mechanism in U-shape Channel[J]. Journal of Irrigation and Drainage, 2006, 25(2): 8-11.

[7] 李甲林, 王正中, 杜成义. 渠道滤透式刚柔耦合衬护结构经济特性分析[J]. 灌溉排水学报, 2006, 25(2): 58-64.

LI Jialin, WANG Zhengzhong, DU Chengyi. Analysis on economic characteristics of channel system with infiltrating-structure and integrated rigidity materials and pliable stuff[J]. Journal of Irrigation and Drainage, 2006, 25(2): 58-64.

[8] 唐少容, 王红雨, 李存云. 考虑衬砌板跨度影响的U型渠道热-力耦合研究[J]. 灌溉排水学报, 2015, 34(11): 65-69.

TANG Shaorong, WANG Hongyu, LI Cunyun. Temperature-stress coupling of U-shaped canal considering the effects of lining’ span[J]. Journal of Irrigation and Drainage, 2015, 34(11): 65-69.

[9] 王正中. 梯形渠道砼衬砌冻胀破坏的力学模型研究[J]. 农业工程学报, 2004, 20(3): 24-29.

WANG Zhengzhong. Establishment and application of mechanics models of frost heaving damage of concrete lining trapezoidal open canal[J]. Transactions of the Chinese Society of Agricultural Engineering, 2004, 20(3): 24-29.

[10] 肖旻, 李寿宁, 贺兴宏. 梯形渠道砼衬砌冻胀破坏力学分析[J]. 灌溉排水学报, 2011, 30(1): 89-93.

XIAO Min, LI Shouning, HE Xinghong. An approach to the mechanics analysis of frost heaving damage of concrete lining trapezoidal open canal[J]. Journal of Irrigation and Drainage, 2011, 30(1): 89-93.

[11] 申向东, 郑玉佩, 王丽萍. 混凝土预制板衬砌梯形断面渠道的冻胀破坏力学分析[J]. 农业工程学报, 2012, 28(16): 80-85.

SHEN Xiangdong, ZHENG Yupei, WANG Liping. Stress analysis of frost heave for precast concrete panel lining trapezoidal cross-section channel[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(16): 80-85.

[12] 肖旻, 王正中, 刘铨鸿, 等. 开放系统预制混凝土梯形渠道冻胀破坏力学模型及验证[J]. 农业工程学报, 2016, 32(19): 100-105.

XIAO Min, WANG Zhengzhong, LIU Quanhong, et al. Mechanical model and validation of frost heave damage of precast concrete slab lining trapezoidal canal in open system[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(19): 100-105.

[13] 宋玲, 欧阳辉, 余书超, 等. 混凝土防渗渠道冬季输水运行中冻胀与抗冻胀力验算[J]. 农业工程学报, 2015, 31(18): 114-120.

SONG Ling, OUYANG Hui, YU Shuchao, et al. Frozen heaving and capacity of frozen heaving resistance of trapezoidal concrete lining canal with water in winter[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(18): 114-120.

[14] 唐少容, 王红雨. 三板拼接式小型U形混凝土衬砌渠道冻胀破坏力学模型[J]. 农业工程学报, 2016, 32(11): 159-166.

TANG Shaorong, WANG Hongyu. Mechanical model of small U-shaped concrete lining canal with three arc-plates under frost heaving[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(11): 159-166.

[15] 葛建锐, 王正中, 牛永红, 等. 冰盖输水衬砌渠道冰冻破坏的弹性地基梁统一模型[J]. 农业工程学报, 2020, 36(1): 90-98.

GE Jianrui, WANG Zhengzhong, NIU Yonghong, et al. Elastic foundation beam unified model for ice and frost damage concrete canal of water delivery under ice cover[J]. Transactions of the Chinese Society of Agricultural Engineering, 2020, 36(1): 90-98.

[16] 安鹏, 邢义川, 张爱军, 等. 弧底梯形渠道抗冻胀结构优化与数值模拟[J]. 灌溉排水学报, 2017, 36(11): 56-62.

AN Peng, XING Yichuan, ZHANG Aijun, et al. Optimal analysis of anti-frost heaping canal with cross section of trapezoidal slopes and curved bed[J]. Journal of Irrigation and Drainage, 2017, 36(11): 56-62.

[17] 李宏波, 田军仓, 夏天, 等. 一种用挠度方程计算渠道冻胀内力的方法[J]. 灌溉排水学报, 2018, 37(2): 77-81.

LI Hongbo, TIAN Juncang, XIA Tian, et al. Calculation method for frost heaving force of canal based on deflection equations[J]. Journal of Irrigation and Drainage, 2018, 37(2): 77-81.

[18] 刘东, 胡宇祥, 付强, 等. 北方灌区混凝土衬砌渠道断面优化及参数分析[J]. 农业工程学报, 2015, 31(20): 107-114.

LIU Dong, HU Yuxiang, FU Qiang, et al. Optimization and parameter analysis for channel cross section with concrete lining in northern irrigation district[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(20): 107-114.

[19] QING Zipng, LAI Yuanming, TIAN Yan, et al. Frost-heaving mechanical model for concrete face slabs of earthen dams in cold regions[J]. Cold Regions Science and Technology, 2019, 161(1): 91-98.

[20] 陈肖柏, 刘建坤, 刘鸿绪, 等. 土的冻结作用与地基[M]. 北京: 科学出版社, 2006.

CHEN Xiaobai, LIU Jiankun, LIU Hongxu, et al. Frozen soil freezing process and foundation[M]. Beijing: Science China Press, 2006.

[21] 李甲林, 王正中. 渠道衬砌冻胀破坏力学模型及防冻胀结构[M]. 北京: 中国水利水电出版社, 2013.

LI Jialin, WANG Zhengzhong. Mechanical model and structure for frost-heaving damage resistance of concrete lining canals[M]. Beijing: China Water&Power Press, 2013.

[22] 王正中, 李甲林, 陈涛, 等. 弧底梯形渠道砼衬砌冻胀破坏的力学模型研究[J]. 农业工程学报, 2008, 24(1): 18-23.

WANG Zhengzhong, LI Jialin, CHEN Tao, et al. Mechanics models of frost-heaving damage of concrete lining trapezoidal canal with arc-bottom[J]. Transactions of the Chinese Society of Agricultural Engineering, 2008, 24(1): 18-23.

[23] 李学军, 费良军, 李改琴. 大型U形混凝土衬砌渠道季节性冻融水热耦合模型研究[J]. 农业工程学报, 2008, 24(1): 13-17.

LI Xuejun, FEI Liangjun, LI Gaiqin. Model of coupled heat-fluid transport of U-shape canal lining with concrete during seasonal freezing and thawing stage[J]. Transactions of the Chinese Society of Agricultural Engineering, 2008, 24(1): 13-17.

[24] 黄义, 何芳社. 弹性地基上的梁、板、壳[M]. 北京: 科学出版社, 2005.

HUANG Yi, HE Fangshe. Beams, plates, shells on elastic foundation[M]. Beijing: Science China Press, 2005.

[25] SELVADURAL A P S. Elastic Analysis of soil-foundation interaction[M]. New York: Elsevier Scientific Publishing Company, 1979.

[26] 肖旻, 王正中, 刘铨鸿, 等. 考虑冻土与结构相互作用的梯形渠道冻胀破坏弹性地基梁模型[J]. 水利学报, 2017, 48(10): 1 229-1 239.

XIAO Min, WANG Zhengzhong, LIU Quanhong, et al. Elastic foundation beam model of frost heave of trapezoidal canal considering interaction between frozen soil and lining structure[J]. Journal of Hydraulic Engineering, 2017, 48(10): 1 229-1 239.

[27] 葛建锐, 牛永红, 王正中, 等. 考虑冰盖生消和冰-结构-冻土协同作用的渠道弹性地基梁模型[J]. 水利学报, 2021, 52(14): 215-228.

GE Jianrui, NIU Yonghong, WANG Zhengzhong, et al. Elastic foundation beam model of canal considering ice cover formation decaying and coupling effect between ice-structure-frozen soil[J]. Journal of Hydraulic Engineering, 2021, 52(14): 215-228.

[28] 李安国, 李浩, 陈清华. 渠道基土冻胀预报的研究[J]. 西北水资源与水工程学报, 1993, 4(3): 17-23.

LI Anguo, LI Hao, CHEN Qinghua. Study on the prediction of frost heave in the bedsoil of canals[J]. Journal of Water Resource & Water Engineering, 1993, 4(3): 17-23.

[29] 安鹏, 邢义川, 张爱军. 基于部分保温法的渠道保温板厚度计算与数值模拟[J]. 农业工程学报, 2013, 29(17): 54-62.

AN Peng, XING Yichuan, ZHANG Aijun. Thickness calculation and numerical simulation of insulation board for canal using partial insulation method[J]. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(17): 54-62.

[30] 李宗利, 姚希望, 张锐, 等. 考虑基土不均匀冻胀的梯形渠道混凝土衬砌冻胀弹性地基梁力学模型[J]. 农业工程学报, 2020, 36(21): 114-121.

LI Zongli, YAO Xiwang, ZHANG Rui, et al. Frost heave mechanical model of concrete lining trapezoidal canal considering nonuniform frost heave of foundation soil based on elastic foundation beam theory[J]. Transactions of the Chinese Society of Agricultural Engineering, 2020, 36(21): 114-121.

[31] 周继凯, 杜钦庆. 考虑水平力作用的改进型Winkler地基模型[J]. 河海大学学报(自然科学版), 2004, 32(6): 669-673.

ZHOU Jikai, DU Qinqing. Modified Winkler foundation model with horizontal force taken into account[J]. Journal of Hohai University(Natural Science), 2004, 32(6): 669-673.

[32] 田亚护, 胡康琼, 邰博文, 等. 不同因素对排水沟渠水平冻胀力的影响[J]．岩土力学, 2018, 39(2): 553-560．

TIAN Yahu, HU Kangqiong, TAI Bowen, et al. Influence of different factors on horizontal frost heaving force against canal[J]. Rock and Soil Mechanics, 2018, 39(2): 553-560.

[33] 田亚护, 沈宇鹏, 隗新宇, 等. 多年冻土区路基U型水沟热-力耦合理论分析及现场试验[J]. 铁道学报, 2015, 37(7): 92-97.

TIAN Yahu, SHEN Yupeng, WEI Xinyu, et al. Theoretical analysis of thermo-mechanical coupling and field test on U-type canal of embankment in permafrost regions[J]. Journal of the China Railway Society, 2015, 37(7): 92-97.

Mechanical Analysis of Frost Heave of Trapezoidal Canal in Frozen Soils with Shallow Groundwater Table

XIAO Min1, XIONG Zhihao1, WU Lang1*, CUI Hao1, YANG Xiaosong2, GE Jianrui3

(1. School of Civil Engineering, Jiangxi Science&Technology Normal University, Nanchang 330013, China;2. College of Water Conservancy and Construction Engineering, Tarim University, Alaer 843300, China;3. College of Energy and Power Engineering, Lanzhou University of Technology, Lanzhou 730050, China)

【Objective】Frost heave is a hazard damaging canals constructed in frozen soils with shallow groundwater table. Taking trapezoidal canals with arc bottoms as an example, this paper investigated the mechanisms underlying the formation of frost heave and its dependance on groundwater table depth.【Method】The analysis was based on the Winkler assumption and that the height of the arc was much less than overall depth of the canal. We proposed a method to calculate the variation of normal force over the frost heave force, as well as the distribution of tangential freezing force over the curved segments of the canal linings. A mechanical model was constructed to analyze the damages caused by frost heave. 【Result】The transverse difference in the distribution of the sectional internal force and the frost heave force both increased as the depth of groundwater table decreasedThe effect of groundwater table depth on distribution of the sectional internal force and frost heave force decreased as the depth of the groundwater table increased. Adequate time and source for water recharge and transversely uneven distribution of frost heave force are the main cause of frost heave damage to the canals. 【Conclusion】The proposed model describes the mechanical characteristic of the canals due the impact of frost heave reasonably well, and the calculated are accurate and reliable.The proposed method and results provide a tool to help design canals to improve the resistance against frost heave damages.

frost soil engineering; irrigation canals; mechanical model; trapezoidal canal with shallow arc-bottom; high groundwater level

1672 - 3317（2022）07 - 0104 - 07

S277；TV67

A

10.13522/j.cnki.ggps.2022024

肖旻, 熊志豪, 吴浪, 等. 高地下水位冻土区弧形底浅拱梯形渠道冻胀力学分析[J]. 灌溉排水学报, 2022, 41(7): 104-110.

XIAO Min, XIONG Zhihao, WU Lang, et al. Mechanical Analysis of Frost Heave of Trapezoidal Canal in Frozen Soils with Shallow Groundwater Table[J]. Journal of Irrigation and Drainage, 2022, 41(7): 104-110.

2022-02-22

国家重点研发计划重点专项项目（2017YFC0405100）；国家自然科学基金项目（U2003108，51641903，51869029）；江西科技师范大学博士科研启动基金项目（2019BSQD11）

肖旻（1987-），男。博士，主要从事冻土工程研究。E-mail: xmhdts@qq.com

吴浪（1981-），男。副教授，博士，主要从事冻土工程研究。E-mail: 348385613@qq.com

责任编辑：白芳芳