基于相位展开及拼接算法的一种高精度大量程宽光谱干涉显微术
2022-08-07赵文豪尹韶云胡建明王金玉
赵文豪, 李 俊, 杜 凯, 熊 亮, 尹韶云, 胡建明, 王金玉*
1. 中国科学院重庆绿色智能技术研究院, 重庆 400714
2. 中国科学院大学, 北京 100049
3. 重庆师范大学物理与电子工程学院, 重庆 401331
引 言
宽光谱干涉显微术因非接触、 无损和快速等优点被广泛应用于高精密检测领域[1-3]。 系统解算样品形貌通常采用垂直扫描干涉术(VSI)[4-5]对亚微米至毫米级特征进行测量, 以及相移干涉术(PSI)[6-7]对纳米级特征进行测量。 其中, 垂直扫描干涉术沿光轴运动显微物镜焦面并采集干涉图像序列, 根据各像素点干涉信号的零光程差位置解算样品高度信息, 虽然其精度只有亚微米级, 该方法具有量程较大的优点。 而相移干涉术原理是在单一焦面位置采集若干带有样品表面信息的干涉条纹图像, 计算其相位信息, 以获得样品表面高度分布[8-9], 其精度可以达到纳米级, 但通常仅用于平滑表面, 高度变化对应的相位信息应包裹在[-π, π]区间内。
为了实现高精度、 大量程宽光谱干涉显微测量, 研究人员采用包裹相位展开算法[10-11]。 对于反射式宽光谱干涉显微系统, 当待测物体表面形貌变化大于1/2波长时, 对应相位就会超出[-π, π]区间, 由反三角函数取模压缩到[-π, π]区间出现相位跳变, 此时相位分布称为包裹相位。 相位展开算法将包裹相位图中每个像素点相位值加上或减去若干2π整数倍以获取真实相位, 进而解算出高度分布。 包裹相位展开不仅应用于宽光谱干涉显微术, 也是数字全息技术, 光栅投影测量技术, 合成孔径雷达等技术的关键步骤[12-14]。 包裹相位展开的效果影响着测量结果的准确性。 目前主流的包裹展开算法主要分为两种: 路径跟踪算法和路径无关算法[15]。 路径跟踪算法的效果取决于相位展开时所选择的积分路径, 选择不同路径进行相位展开, 会得到不同的展开结果。 Goldstein提出的枝切法(Branch-Cut)[16]是一种经典的路径跟踪算法, 通过计算残差点的正负极性来设置枝切线, 使解包裹的积分路线上的正负极性达到平衡以获取真实相位。 路径跟踪算法在多数情况下能取得不错的效果, 但当积分路径经过的像素点间存在有噪声、 欠采样, 断点等情形时, 使用路径跟踪算法对相位展开无法得到理想结果[17-18]。 最小范数法[19-20]是路径无关算法的代表, 其中最经典的是最小二乘法(Least-Square)[21], 最小范数展开过程被视为一个全局优化问题, 在保证包裹相位微分和解包裹相位局部微分相等的前提下, 使解包裹相位最逼近真实相位, 即包裹相位微分和预测真实相位局部微分之差最小。 这种算法具有平滑作用, 在某些情况下会导致误差传递。
但是, 宽光谱干涉显微系统在指定焦面位置所获得的条纹质量, 依赖于显微物镜焦深范围、 宽光谱光源的相干长度, 当样品表面起伏超出焦深或者光源相干长度的限定范围时, 条纹模糊或对比度丧失, 包裹相位展开所获得的结果产生较大误差甚至错误。
本论文提出一种新的高精度、 大量程宽光谱干涉显微测量方法: 以干涉条纹调制度量化条纹质量, 定义当前焦面位置条纹调制度高于设定阈值的区域为理想区域, 即条纹对比度较高、 条纹清晰的区域, 以相位展开算法获得理想区域中的样品高度分布; 纵向移动物镜焦平面, 将不同焦面位置获取的样品高度进行拼接, 可获得扩展量程的高精度形貌测量结果。 经仿真和实验结果验证, 本文提出的相位展开及拼接算法可达到宽光谱干涉显微术中相移干涉测量方法的精度, 并将其量程从数百纳米拓展到数微米。 且理论上本测量方法量程可以覆盖物镜的全工作距离。
1 基于调制度评价函数的相位展开及拼接算法
1.1 宽光谱干涉显微系统
如图1所示, 验证实验采用典型的Linnik对称结构宽光谱白光干涉系统[22], 参考臂和样品臂光路对称用以消除色差。 宽光谱白光光源(LED, Thorlabs M730L4)中心波长为730 nm, 谱宽30 nm, 采取科勒方式获得样品面均匀照明。 分束镜(BS)将照明光束分别照明位于参考臂和采样臂中显微物镜(50×, NA 0.55, Nikon)焦面上的参考镜面和样品面, 并结合双臂反射回光经物镜L(Nikon筒镜, 焦距200 mm)聚焦到像机光敏面, 红色虚线为光源共轭关系, 黑色虚线为物像共轭关系。 双臂干涉条纹图像由CCD(Baumer, VCXU-50M, 像素3.45 μm×3.45 μm, 分辨率2 448×2 048)像机采集。 参考镜面安装压电驱动器(PZT, 迈客荣, PZT150-7-60-VS12) 用于产生周期性机械振荡。 一维位移台Ts0用于垂直调节样品台及样品实现采样焦面调节。 二维位移台Ts1(Thorlabs, MSC202)用于对准样品。 一维位移台Ts2用于调节参考臂长使得参考镜面与样品臂焦面等光程。
1.2 相移干涉术原理
相移干涉术是一种利用相位信息计算样品表面形貌的测量技术, 最开始应用于单色光相移测量系统中, 常见的相移算法有三步相移法、 四步相移法、 五步相移法、 Carre相移法[23-24]等。 下面以四步相移法为例, 简述相移干涉测量技术原理, 在位置n处宽光谱白光干涉信号光强I(n)为
I(n)=I0{1+M(n)cos[φ(n)]}
(1)

图1 宽光谱干涉显微系统原理图
式(1)中,I0为背景光强,M(n)为干涉条纹调制度,φ(n)为双臂相位差。
四步相移过程中, 要求微位移步长为λ0/8,λ0为宽光谱光源中心波长, 其对应的相位变化量为π/2, 微位移系统每次移动结束, 图像采集系统采集一张干涉图像, 不同位置干涉图各像素点的灰度值可以由式(2)表示
(2)
式(2)中,Ii(x,y)为四步相移第i帧干涉图灰度值, 各像素点主相位分布可由式(3)计算
(3)
在编程计算φ(x,y)时, 需要用到四象限反正切函数arctan2f(x,y), 该函数计算所得相位被限制在[-π, π]内, 所以四步相移算法所获得的相位信息φ(x,y)是包裹在[-π, π]区间内的,φ(x,y)被称为包裹相位, 需要进行相位展开以获取真实相位φ(x,y)。 展开后的真实相位可通过式(4)计算样品的高度分布h(x,y)。
(4)
相移干涉术具有纳米级精度, 但仅适用于平滑表面测量, 高度分布所获得的相位包裹在[-π, π]区间内。 研究人员采用包裹相位展开算法以实现高精度、 大量程宽光谱干涉显微测量。
但是, 当样品表面变化过大时, 干涉图离焦区域会变模糊, 该区域对应的测量结果会产生较大误差甚至错误。 同理, 由于宽光谱干涉显微系统一般为反射式, 光束双光程往返使得样品表面起伏超出1/2光源相干长度的区域干涉条纹对比度丧失, 导致系统性测量误差。
1.3 基于调制度评价函数的相位展开及拼接算法
基于调制度评价函数的相位展开及拼接算法作为一种新的高精度、 大量程宽光谱干涉显微测量方法: 以干涉条纹调制度量化条纹质量, 以相位展开算法获得在当前焦面位置理想区域的样品高度分布; 将不同焦面位置获取的样品高度进行拼接, 可获得扩展量程的高精度形貌测量能力。
步骤一: 计算干涉条纹调制度并设置阈值标记理想区域
相对于相位差分方差(PDV)、 最大相位梯度(MPG)等众多的包裹相位质量评价函数, 调制度是一种直接反映干涉图质量好坏的评价函数[25-27]。
像素(x,y)位置条纹调制度M(x,y)定义为,
(5)
式(5)中,N为相移测量的步数,n=1, 2, …,N,In(x,y)为第n帧干涉图灰度值。
以调制度作为干涉图质量评价函数, 我们设置阈值标记干涉信号质量较好区域(理想区域)和干涉质量不佳区域(问题区域), 对调制度大于阈值的像素点进行相位展开, 调制度小于阈值的不进行处理。
某扫描位置计算所得包裹相位值的调制度分布示意图如图2,Ra为调制度大于所设阈值区域,Rb为调制度小于所设阈值区域。 阈值的选择十分关键, 如果阈值设置太大, 会使许多质量尚可的点被遗漏, 阈值设置太小, 则会导致许多质量不好的像素点被认为是可靠的像素点进行相位展开, 可能导致相位展开失败。

图2 阈值化调制度分布示意图
标志矩阵在像素(x,y)处取值Pv(x,y)为
(6)
式(6)中,M(x,y)为调制度,km为设定的阈值, 标志为1的区域为理想区域。
步骤二: 使用相位展开算法展开理想区域包裹相位
菱形相位展开算法(rhombus algorithm)[28]是一种经典的路径跟踪算法, 菱形相位展开算法有着较快的运算速度, 但其抗干扰能力较为一般, 在实际测量中, 由于各种噪声的影响, 菱形相位展开算法所得到的结果并不理想, 由于路径跟随算法积分的累加作用, 展开相位会产生拉线和孤岛效果。 但在本论文中, 设置合适的阈值标记出问题区域和理想区域后, 只对理想区域的包裹相位进行菱形展开, 问题区域不展开, 在不同焦面位置采集干涉图解算真实相位并重复进行以上操作。
菱形相位展开原理如图3所示, 以某起始点(点1)为种子像元, 以此像元为中心向其相邻四个像素点进行扩散解包裹, 起始点邻域的四个像素点展开完成后, 再依次以这四个像素点为中心进行相位展开, 完成下一轮菱形相位展开, 在上一轮已经展开的点不进行展开, 直至所有像素点都被展开。

图3 菱形相位展开算法原理
步骤三: 相位拼接
不同焦面位置解算的真实相位, 需要拼接以获得完整的连续相位分布。 如图4, 位置Ⅰ、 Ⅱ对应的展开相位矩阵R1和R2,R1和R2的重合区域记为R12。
重合区域R12为两次测量标志矩阵均为1的区域, 为了进行相位拼接, 需要计算重合区域的相位值均差Δφ12
(7)
式(7)中,Pv1和Pv2为位置Ⅰ和Ⅱ对应的标志矩阵, ∘为Hardmar积,N12为重合区域像素数, 根据重合区域的相位值均差Δφ12, 不同位置相位分布图按式(8)拼接

图4 两个不同焦面位置展开相位关系图
φstitch(x,y)=
(8)
将所有位置的区域展开相位拼接完后, 即可得到样品完整的相位分布。 减去最小二乘法拟合的平面以去倾斜[29]后再通过式(4)即可得到样品表面高度分布。
2 仿真和实验结果
2.1 仿真
宽光谱干涉显微系统(图1)Ts0垂直位移过程中, 宽光谱白光干涉信号光强[式(1)]为,
(9)
式(9)中,z为垂直扫描位置,z0为干涉臂长,lc为相干长度,λ0为宽光谱白光光源中心波长,k为倾斜因子(样品相对光轴的倾斜程度),I0为背景光强。
在数值模拟中, 以Matlab的peaks函数作为待测物体, 其高度分布如图5(a)所示, 倾斜因子k为0.02。 在焦面位置Ⅰ和Ⅱ分别获取干涉图5(b)和(c), 由于引入了倾斜因子k, 仿真所获得的干涉条纹更接近实际测量中的干涉条纹。 在这两个焦面位置使用四步相移算法获取包裹相位, 计算对应调制度[式(5)]如图5(d)和(e), 在干涉条纹模糊区域调制度较低。

图5 相位展开及拼接仿真
对各位置理想区域展开相位进行拼接, 并利用最小二乘法去倾斜后得到重建后的三维结构如图6所示。 为对比起见, 分别以最小二乘法和枝切法恢复的三维结构图6(a)和图6(b), 可以看出, 本文提出的相位展开及拼接结果图6(c)优势明显, 可以很好克服条纹模糊等情况下包裹相位不准确带来的问题。
2.2 实验
实验采取的待测微纳结构是某种加工后硅片表面的半球形结构, 其粗高度为3~4 μm, 本次实验对半球形阵列中的某一个半球形进行测量。
在实验过程中, 分别在扫描位置Ⅰ, Ⅱ和Ⅲ处, 驱动压电陶瓷步进N8进行四步位移并采集干涉图像, 共计12张干涉图像, 并使用四步相移法获取三个不同位置的包裹相位, 再根据评价函数以及阈值标记出问题区域和理想区域, 对理想区域进行相位展开, 最后依据式(8)将三个位置的理想区域展开相位进行拼接, 即可得到整个待测物体的完整三维面型。

图6 通过三种算法仿真获得的三维结构
图7(a)为微纳结构的灰度图, (b)—(d)为三个典型位置的调制度分布。 在实际测量过程中, 由于显微物镜焦深限制和待测物体部分反射较差等原因导致部分区域包裹相位质量较差, 必须设置一个合适的阈值以区分问题区域和理想区域, 经过优化, 我们设置阈值0.3进行三维重建, 为了使实验结果更加直观, 分别采用最小二乘法、 枝切法、 相位展开及拼接方法对测试微纳结构进行三维重建, 并提取y=500时的数据进行对比。
图8(a)和(d)为最小二乘法所恢复的三维面型和红线所示横截面内高度分布, 超出了粗略高度约10多μm, 误差严重。 图8(b)是枝切法恢复的三维面型, 明显可见其在边缘出现了拉丝现象, 图8(e)所展示的横截面可以看出枝切法恢复的横截面存在大量噪声。 本文所提方法解得三维面型图8(c)和在横截面图8(f), 由于测试样品底部区域反射率过低, 干涉条纹不明显, 获取包裹相位出现误差, 导致展开相位横截面在底部产生了噪声, 但其对整体高度的还原并无影响, 高精度还原了测试微纳结构的三维形貌。
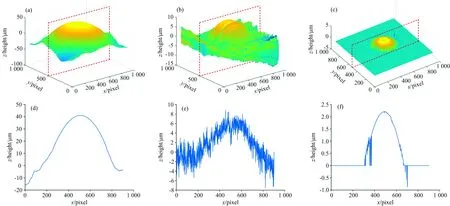
图8 三种算法重建结果
3 结 论
基于相移干涉算法的宽光谱干涉显微术, 具有纳米级高精度, 但仅适用于平滑表面测量, 高度分布对应的相位应包裹在[-π, π]区间内。 采用包裹相位展开算法时, 量程受到显微物镜焦深范围、 宽广谱光源干涉长度限制, 当样品表面高度变化过大时, 超范围区域会变模糊或失去对比度, 导致测量误差或者错误, 相位展开算法无法给出正确样品高度分布。
提出一种基于相位展开及拼接算法的高精度、 大量程宽光谱干涉显微测量方法。 仿真和实验结果验证了该方法的有效性。 不仅可保持宽光谱干涉显微术中相移干涉术的纳米级精度, 相位展开可以将量程拓展至波长量级, 进而通过相位拼接将其量程从数百纳米拓展到数微米。
本文提出测量方法将不同焦面条纹调制度高于设定阈值的区域定义为理想区域, 以纳米精度解算出对应区域样品的高度分布。 而不同的理想区域通过垂直位移台移动显微物镜焦面解算获得。 测量过程中, 相邻理想区域对应的位移距离应保证二者之间存在重叠区域(图4)以实现高精度相位拼接[式(7)]。 由于相邻理想区域之间的部分区域重叠, 确保了系统测量精度不依赖于位移部件。 本文提出测量方法整个扩展量程中可达到纳米级精度, 且理论上其量程可以拓展到显微物镜的全工作距离。
