多约束强化学习最优智能滑翔制导方法

朱建文，赵长见，李小平，包为民, 3

(1. 西安电子科技大学 空间科学与技术学院， 西安 710126; 2. 中国运载火箭技术研究院， 北京 100076；3. 中国航天科技集团公司， 北京 100048)

制导是高超声速飞行器的核心技术之一，要求控制飞行器在满足多种过程约束的条件下完成给定的飞行任务。滑翔制导面临复杂飞行环境、强不确定性、多样化飞行任务、多种过程与终端约束等挑战。因此，滑翔制导方法需要保证对终端约束的高精度性、过程偏差的鲁棒性以及多样化制导任务的自适应性。

在滑翔制导领域，标准轨迹跟踪是最传统的滑翔制导方法，该方法主要分为两部分：首先是满足多种过程约束与终端约束的标准轨迹设计，其次是保证制导精度与鲁棒性的制导指令解算，即轨迹跟踪[1]。该方法具有较强的可靠性，并能减小在线计算量，但在飞行任务改变时需要重新设计标准弹道与跟踪控制参数，限制了对不同任务的适应能力[2]。预测校正需要在线预测终端状态，并根据终端误差校正当前制导参数[3]。然而，解析预测校正方法需要对运动模型进行大量简化，难以保证制导精度；数值预测校正方法需要复杂的在线计算，限制了实时性[4]。最优滑翔制导以滑翔飞行特性为前提，基于两点边值问题，利用极大值原理推导多约束制导律，但其速度控制精度受反馈系数的影响较大，通常需要人为地调整[5-6]。

以机器学习为主的人工智能是当前的研究热门主题，强化学习作为一种体现智能决策的算法，得到了众多学者的认可，并在路径规划与参数确定领域有初步的研究[7]。文献[8]研究了一种高阶强化学习问题，并通过仿真与实际飞行测试进行验证，试验设计为：利用四旋翼在事先完全未知的环境中采集灾害点图像，并学习获得关注点以及前往该位置的最有效路径。针对拦截制导问题，Gaudet利用强化学习设计了关于最优气动特性以及传感器和驾驶仪噪声与时延的寻的制导律，但未明确给出状态与动作空间模型[9]。进一步, 针对只有视线角与角速率信息的大气层外机动目标拦截问题，元强化学习被用于优化目标加速度的跟踪策略，该策略相对于零化脱靶量拦截制导具有更明显的优势[10]。文献[11]利用强化学习生成参考倾侧角指令，并将轨迹的生成问题简化为“状态-动作”值的简单搜索问题，利用深度强化学习实现飞行器着陆制导。文献[12]构建了可解决飞行器着陆制导问题的训练环境模型，并且智能体获取飞行状态以生成控制动作，其中深度Q网络被用于证明控制方法的可行性。总之，强化学习在智能体规划与控制方面已经有一定的研究，但是在高超声速飞行器的制导领域仍未见公开成果。

本文针对传统滑翔制导方法存在的关键问题，结合强化学习方法的优势，提出一种基于最优制导、预测校正以及强化学习的多约束智能滑翔制导策略。首先，利用最优滑翔制导方法以满足终端经纬度、高度以及速度倾角约束；其次，提出基于侧向机动的速度控制策略，并综合考虑滑翔飞行特性与侧向机动飞行对终端速度进行了解析预测；最后建立强化学习的框架模型，采用Q-Learning对速度控制中的机动幅值进行智能调整，以保证终端速度控制精度。该制导策略将降低强化学习的维数，并保证学习效率，进而实现多约束自适应制导。

1 智能滑翔制导问题与策略

智能滑翔制导需要飞行器与环境进行交互与感知，以提升飞行任务在线变更时的自适应能力。滑翔飞行器所处的临近空间极其复杂，飞行距离远，大气密度与自身气动系数都存在较大偏差，利用恒定的参数控制整个滑翔飞行必然存在较大缺陷。另外，滑翔飞行器面临着多样化的飞行任务，甚至飞行任务在线变更的情况，因此制导参数更需要根据实际飞行状态与当前任务进行在线调整。针对上述滑翔制导问题，提出如图1所示的离线强化学习加在线智能调参的制导策略。

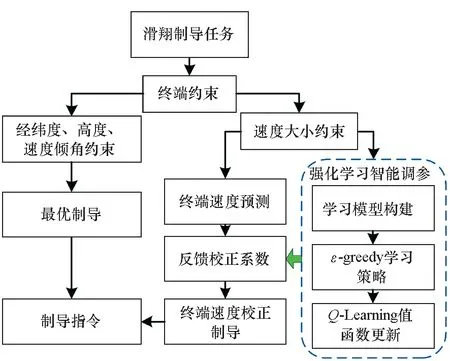
图1 智能滑翔制导策略框图Fig.1 Intelligent gliding guidance strategy

首先，在制导策略上，结合最优制导、预测校正与强化学习以实现制导任务。解析最优制导能够满足经纬度、高度以及速度倾角约束，采用预测校正方法控制终端速度大小。针对滑翔飞行中的多源不确定性与多样化飞行任务，尤其是终端速度预测误差对制导性能的影响问题，本文进一步利用强化学习对制导参数，即速度控制中机动幅值进行在线智能调整。

然后，在学习方法上，采用强化学习以实现智能调参，该方法需要构建状态空间与动作空间，设计回报函数，通过反复迭代选取动作指令以获得最大的回报。为保证强化学习的效率，速度控制中机动幅值的自适应调整是强化学习的唯一任务。因此，将终端速度大小作为状态变量，将机动幅值作为动作变量，并通过合理的离散化处理以降低状态空间与动作空间的维数。进一步，在突出终端速度控制的基础上考虑其他制导任务，设计回报函数。

最后，采用ε-greedy策略进行迭代学习，并在值函数的更新算法上，利用目前强化学习中典型的Q-Learning方法进行更新。

2 最优滑翔制导与速度预测

根据智能制导策略，采用解析最优制导方法以满足终端经纬度、高度以及速度倾角约束，进一步在侧向增加机动飞行，利用预测校正方法控制终端速度大小约束。

2.1 最优滑翔制导律

滑翔制导的任务是基于当前状态生成制导指令以满足终端多种约束。当前状态包括速度v、速度倾角θ、速度方位角σ、经度λ、纬度φ以及高度h，终端约束为：

xf=(vf,θf,λf,φf,hf)

(1)

在前期的研究中[5]，基于准平衡滑翔条件，以需要过载为控制量，建立了能量损耗最小的性能指标，在纵向与侧向分别设计了能够满足终端经纬度、高度以及速度倾角约束的最优制导律，即需要过载指令为[5]：

(2)

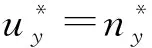
(3)

基于式(2)给出的过载指令，控制量攻角α与倾侧角υ计算为：

(4)

其中，ρ为当前高度处的大气密度，Sm为飞行器参考面积，CL(Ma,α)为由马赫数与攻角确定的升力系数，g0为海平面处的引力加速度。式(4)第一式需要反差值计算以获得攻角。

2.2 终端速度解析预测与分析

滑翔终端速度控制的前提是能够快速准确获得终端速度，因此采用解析方法来预测终端速度。由于滑翔飞行器的主要受力为空气动力与地球引力，因此速度微分为：

(5)

其中，D为当前气动阻力，m为飞行器质量。式(5)包含了所有的飞行状态，求解方程(5)还需要其他微分方程，导致解析求解无法实现。因此，为解析获得终端速度，需要根据滑翔飞行特性对式(5)进行合理转化。速度控制的目的是在给定的射程处满足速度大小约束，而对终端到达时间无约束，因此可基于射程微分对式(5)进行重构：

(6)

进一步，利用“平均法”对式(6)中的状态参数进行固化。将待飞射程内的时变阻力假设为当前实际阻力Dc与终端阻力Df的平均值。在滑翔飞行的末段，飞行高度相对较低，飞行器具有足够大的升力以实现平衡滑翔飞行。因此，气动升力的纵向分量约等于引力。

Lfcosυ≈mg

(7)

其中，Lf为飞行末段的气动升力。当飞行器处于滑翔飞行状态时，升阻比RL/D保持较大且变化幅度很小，意味着在一个制导周期内RL/D可被认为是常值。因此，飞行终端的气动阻力可间接表达为：

(8)

当前气动阻力Dc与终端气动阻力Df的平均值为：

(9)

同理，对式(6)中的速度倾角进行转化。当飞行器处于滑翔飞行状态时，速度倾角及其变化率都很小。因此，存在以下针对速度倾角的简化：

(10)

由式(6)与式(9)可知，为解析预测终端速度，需要对阻力中的倾侧角υ进行转化。倾侧角可通过最优制导律并由式(4)的第二式计算获得，但终端速度大小不可控。机动飞行可增加额外的能量损耗，而飞行器需要在纵向保持平衡滑翔飞行，因此在原最优制导律(2)的基础之上，引入侧向机动飞行以控制终端速度大小。考虑机动飞行的倾侧角为：

(11)

其中，nvc是用于控制终端速度的机动过载。机动飞行是对原最优制导律的破坏，因此设计机动过载需要尽量减小其对终端制导精度的影响。整周期的侧向正弦机动能够增加能量损耗，并能使机动产生的侧向误差正负相消。设计机动过载为：

(12)

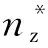
(13)

为计算倾侧角，需要进一步对“未来”飞行中的过载指令进行解析简化。平衡滑翔是滑翔飞行器的主要飞行特性之一，飞行器的高度变化很平缓，即纵向需要过载基本保持不变。因此，可基于当前需要过载与终端过载计算滑翔全程飞行的平均过载：

(14)

其中，“1”为终端过载，表示末端飞行器严格地等高飞行。结合式(13)与式(14)中的平均过载，可计算倾侧角为：

(15)

利用式(9)中的平均阻力、式(10)中的平均速度倾角以及式(15)中的平均倾侧角代替式(6)中的当前飞行状态，则式(6)可转化为：

(16)

从当前状态到终端状态，对式(16)左右两边求定积分，可获得终端速度的解析预测值。

(17)

由式(17)可知，机动幅值Avc越大，则能量消耗越大，即终端速度越小。理论上，通过设置不同的机动幅值Avc，便可获得不同的终端速度。相反地，也可基于式(17)，根据终端速度约束解析计算出需要的机动幅值。然而，终端速度解析预测必然存在偏差，直接根据式(17)解析计算机动幅值将影响速度控制精度。为此，通过对机动幅值Avc进行智能调整，以控制终端速度大小。需要说明：终端预测速度必然存在误差，主要来源于剩余射程内飞行器受力的未知性，故采用平均法对未知的时变受力进行固化假设。随着滑翔飞行的不断推进，上述受力假设的精度不断提高，并且剩余射程不断减小，致使终端速度的预测与控制精度不断提高。

3 强化学习与Q-Learning

强化学习把学习看作试探评价过程，智能体选择一个动作用于环境，环境接受该动作后状态发生变化，同时产生一个强化信号(奖或惩)反馈给智能体，智能体根据强化信号和环境当前状态再选择下一个动作，选择的原则是使受到正强化(奖)的概率增大。选择的动作不仅影响立即强化值，而且影响环境下一时刻的状态及最终的强化值。强化学习的常见模型是标准的马尔可夫决策过程(Markov decision process, MDP)。一个MDP由五元素构成：状态集合S、动作集合A、状态转移概率Psa、折扣系数γ∈[0,1)、回报函数R[13]。

Q-Learning是强化学习的一种经典学习方法，其中Q(s,a)表示状态行为值，即在当期策略下，当前状态s与动作a对应的值函数的具体取值。若状态集合为p维，动作集合为n维，则Q(s,a)为p×n维的表格，因此可称之为Q表。Q-Learning中值函数的更新算法为：

(18)

具体的Q-Learning算法步骤如下：

1)人为地以任意形式初始化Q(s,a)表格。

2)对于每次学习回合，给定一个初始状态s。

3)执行以下操作：

①利用当前的Q值，确定当前的行为a；

②执行当前的行为a，获得量化的回报R与下一状态s′；

③基于式(18)更新Q表；

④更新当前的状态s←s′；

⑤当s满足终止状态时，结束当前回合的学习；

4)基于已更新的Q表，重复执行步骤3，直至满足学习次数。

4 速度反馈系数的智能调整

在满足终端速度约束的预测校正制导中，机动幅值的智能调整是消除过程偏差与速度预测误差并应对多样化飞行任务的有效手段。由于终端速度只与当前和未来机动幅值相关，而与过去的信息无关，因此机动幅值的确定符合MDP过程。根据强化学习与Q-Learning的需求，需要根据实际制导任务搭建智能调参模型、设计状态与动作空间以及回报函数，基于强化学习的智能调参逻辑如图2所示。

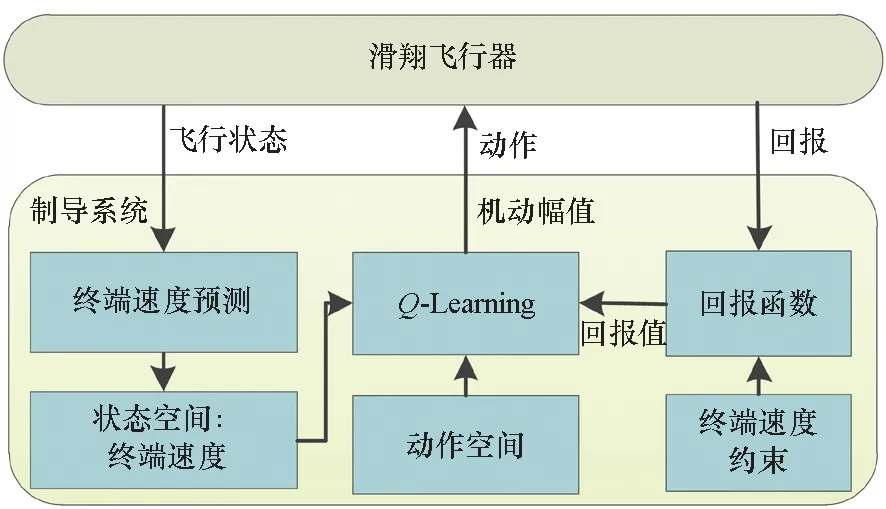
图2 强化学习智能调参框图Fig.2 Intelligent parameter modification via reinforcement learning

4.1 行为策略设计

采用ε-greedy策略，通过学习确定满足终端速度约束的机动幅值。在第一次调参中，利用随机方法对Q表进行初始化以探索更多的状态与动作，在后续调参中继承上一次调参获得的Q表以加快迭代收敛速率。另外，为了充分发挥Q-Learning算法的探索和寻优能力，在学习的前期ε可选择较大，以探索更多的状态与动作，在后期逐渐减小使得滑翔制导在已有经验的基础上做出正确的动作，进而以保证终端制导精度。基于Q-Learning的机动幅值智能调参流程如图3所示。

图3 Q-Learning机动幅值智能调参流程Fig.3 Intelligent modification flow of maneuvering amplitude via Q-Learning

4.2 状态空间设计

状态空间是强化学习中必不可少的元素，是反应飞行过程状态或者终端状态的数据集合，并且必须包含所有可能的状态参数取值。本文利用智能调参方法满足终端速度大小约束，因此可设计状态空间为终端速度组成的数据集合。滑翔制导是时间连续的质心控制问题，其终端速度也必然是时间连续的。因此，在利用离散化的强化学习进行智能调参时，需要对终端速度进行离散化，即状态空间为终端速度组成的离散化的数据集合。

由于滑翔飞行器自身性能约束的影响，设置终端速度的范围为[2 000, 4 000]m/s，进一步将其离散为等间隔的状态空间，离散点数为51个，间隔为40 m/s。

4.3 动作空间设计

根据强化学习中对动作空间的定义，“动作”需要对上述“状态”产生影响。影响状态，即终端速度的因素有很多，包括当前的飞行状态以及上下左右等机动飞行。过复杂的动作空间将增大动作的搜索空间，进而影响学习效率。针对该问题，基于所提出的终端速度的预测校正制导方法，设计“动作”为能够直接影响飞行以及终端速度大小的机动幅值，即动作空间为基于机动幅值组成的数据集。在前期研究中[5-6]，利用最优制导与机动减速方法生成制导指令，能够使终端速度在2 000～4 000 m/s范围内变化的机动幅值调整范围为0～0.75。因此本文适当扩大该范围至[0, 0.8]，进而设计由30个离散点组成的动作空间：A=(0, 0.1, 0.2, 0.3, 0.35, 0.40, 0.45, 0.5, 0.52， 0.54, 0.56, 0.58, 0.6, 0.62， 0.64, 0.66, 0.68, 0.7, 0.71, 0.72, 0.73, 0.74, 0.75, 0.76, 0.77, 0.78, 0.785,0.79, 0.795,0.8)。

4.4 回报函数设计

量化的回报函数用来判断动作的性能是强化学习的核心所在。强化学习方法的目的是在线修正机动幅值以高精度控制终端速度大小。因此，本文根据终端速度的满足情况设计回报函数为：

(19)

式(19)中回报函数的物理意义是：当预测速度与需要速度之差小于200 m/s时，回报值为负的速度差绝对值；当预测速度远小于需要速度时，过多的能量损耗将导致飞行任务的无法完成，此时应当给予最严厉的“惩罚”；当预测速度远大于需要速度时，过快的飞行速度将导致动压、过载等过程约束的超限，此时给予较严厉的“惩罚”。回报函数(19)设计的目的是控制预测速度与需要速度达到相等，二者越接近则回报值越大，最大回报值为“零”。

至此，式(4)给出的攻角与倾侧角指令计算方法、式(12)中的侧向机动弹道以及基于强化学习获得的机动幅值，可满足终端约束。对于热流、过载以及动压过程约束而言，需要结合当前实际飞行状态将其全部转换为攻角约束，进而实现安全飞行[5-6]。

5 仿真分析

以CAV-H为仿真对象[14]，滑翔飞行初始参数设置为：速度为6 500 m/s，速度倾角为0°，速度方位角与视线方位角相等，位置为[0°E，0°N]，高度为65 km。终端参数为：位置为[95°E，10°N]，高度为30 km，速度倾角为0°，速度大小为2 600 m/s。速度控制的附加侧向机动过载(12)中，机动频率km=3，即飞行器进行3个周期的正弦机动以控制终端速度。在强化学习的参数中，学习周期为800 km，并只在滑翔飞行的前8 000 km范围内进行调参。在ε-greedy中，第一次学习ε1=0.3，第二次学习ε2=0.2，第三次学习ε3=0.1，后续学习全部为0。Q-Learning中的终端速度误差范围为40 m/s，即预测速度与需要速度之差小于该值时，则认为满足终端速度约束。

5.1 基本性能仿真测试

根据参数设置，在滑翔飞行过程中一共进行10次完整的机动幅值调整。图4～5给出了第一次和第七次调参的收敛步数与累计回报值，由仿真结果可知，收敛步数越多，则累计回报值越小。另外，每次调参在经过一定次数的震荡之后都能收敛，收敛之后减速机动幅值的校正次数在2次以内，累计回报值也趋向于稳定的最大值“零”。比较两次调参的效果可知，第七次调参的收敛速率约为第一次的3倍，原因在于：第一次采用了随机方法对Q表进行初始化，且ε设置较大，在学习过程中必然要经历多次“尝试”以获得很多的经验，导致收敛速率降低；后续调参继承了前一次获得的Q表，该表已经包含了能够满足终端速度约束的值函数信息，更加具有经验，因此收敛速率能够有很大的提高。

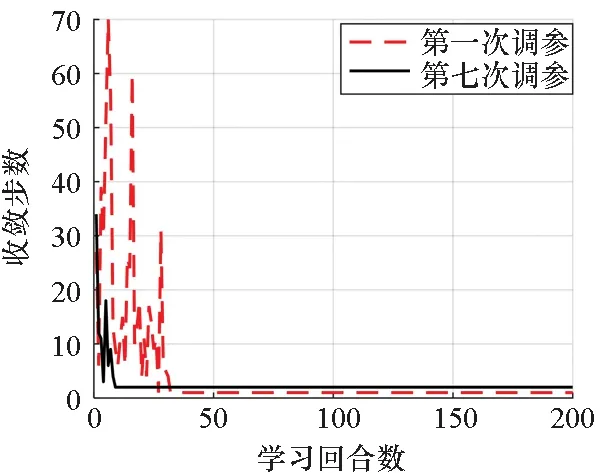
图4 两次调参的收敛步数Fig.4 Convergency steps of two modifications

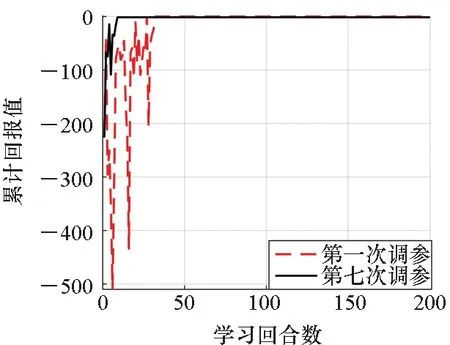
图5 两次调参的累计回报值Fig.5 Reward values of two modifications

利用最优滑翔制导律以及由强化学习确定的机动幅值生成制导指令，主要仿真结果如图6～11所示。由仿真结果可知，智能滑翔制导方法能够控制飞行器满足终端经纬度、高度、速度大小以及倾角约束，位置误差约为12 m，高度误差为0.6 m，速度倾角误差约为-0.011°，速度大小误差为5 m/s。在滑翔初始阶段，尽管有较大的纵向过载指令，但是较高的飞行高度以及较小的大气密度导致飞行器无法实现平衡滑翔，高度与速度倾角存在同步的跳跃。随着高度的不断降低，大气密度不断增加，飞行器具有足够大的升力来实现滑翔飞行，直至目标处。由图6～8可知，侧向过载与倾侧角经历了三个周期的正弦机动，且其机动幅值不断减小，以减小机动对其他制导精度的影响。由于强化学习的周期是800 km，因此机动幅值存在非连续的阶跃变化，不断减小的机动幅值有利于降低机动飞行对制导精度的影响。另外，终端速度的解析预测值接近于速度约束值，且变化幅度很小，为速度的高精度控制奠定了基础。

图6 过载-时间Fig.6 Overload-time

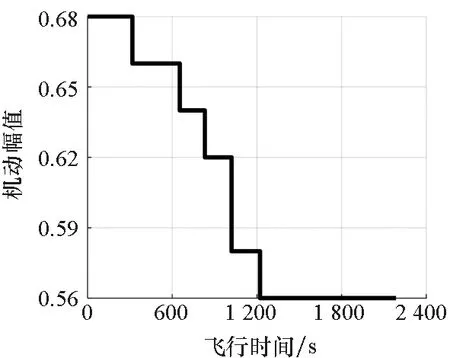
图7 机动幅值-时间Fig.7 Maneuvering amplitude-time

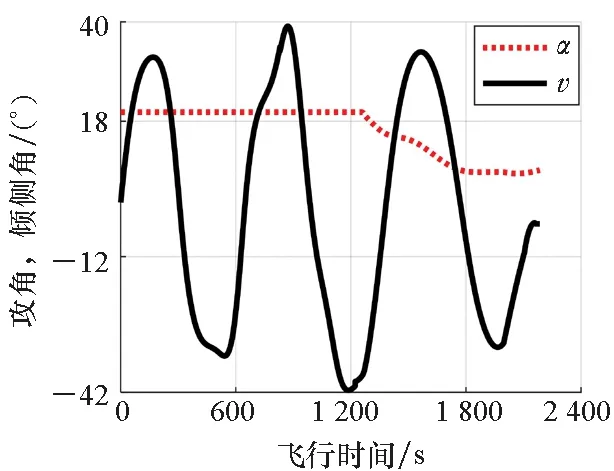
图8 制导指令-时间Fig.8 Guidance commands-time

图9 速度-时间Fig.9 Velocities-time

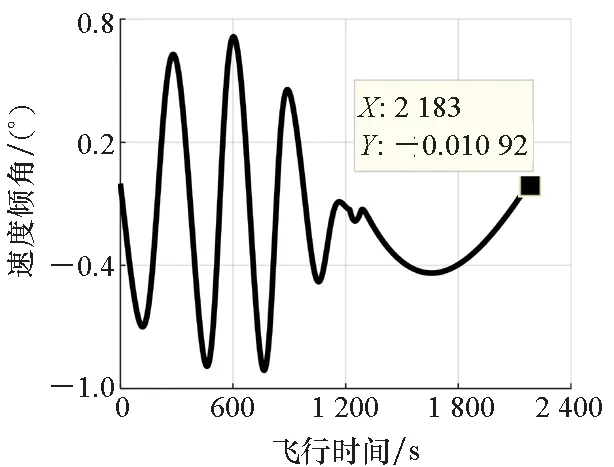
图10 速度倾角-时间Fig.10 Velocity slope angle-time

图11 经度-纬度-高度Fig.11 Longitude-latitude-altitude

5.2 适应性仿真测试

为进一步验证智能滑翔制导方法的适应性，保持终端经纬度、高度以及速度倾角约束不变，设置不同的速度大小约束进行测试，仿真结果如表1与图12所示。由仿真结果可知，智能滑翔制导方法能够根据终端约束值对机动幅值进行智能调整，在保证位置、高度以及速度倾角约束的前提下，仍能满足不同的终端速度约束。随着终端速度的减小，机动幅值不断增大，剧烈的机动飞行导致终端位置与速度倾角误差不断增大。随着飞行器不断接近目标，终端速度预测精度不断提高，机动幅值也不断优化并在飞行后期保持恒定。对比图11与图12中的仿真结果可知，在终端速度约束为2 600 m/s时，出现了不同的终端制导精度，这主要是由于第一次调参采用随机方法对Q表进行初始化，导致学习的结果存在差异，但均未超出终端速度的误差范围。

表1 不同速度约束下的制导精度Tab.1 Guidance accuracies under different terminal velocities

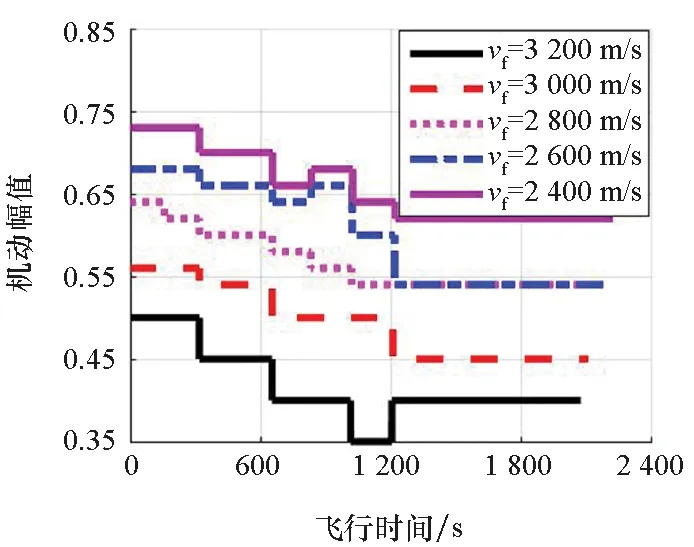
图12 不同速度约束下的机动幅值Fig.12 Maneuvering amplitudes under different terminal velocities

设置相同的终端约束，利用式(17)解析计算机动幅值(G1)，并与智能滑翔制导方法(G2)进行对比分析，仿真结果如表2所示。由仿真结果可知，解析计算机动幅值的方法产生的终端速度误差始终在50 m/s以上，而采用强化学习进行智能调参时，终端速度误差始终未超过30 m/s。智能方法的终端速度误差主要受Q-Learning中的误差范围的影响，意味着终端速度误差的大小是可人为控制的。然而，受动作与状态空间中各元素间隔大小的影响，以及学习计算效率的考虑，该误差范围不能太小，以免造成学习的失败。

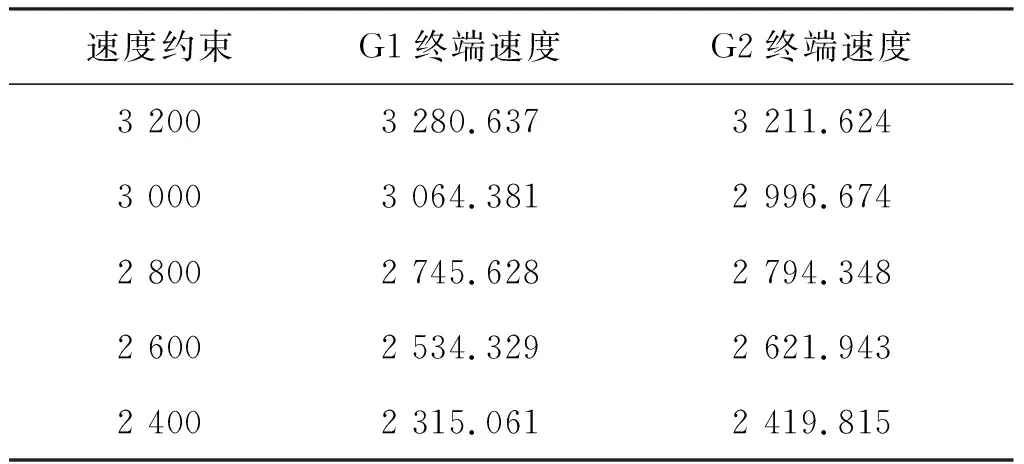
表2 制导律G1与G2性能对比Tab.2 Performance comparison between G1 and G2 单位：m/s

6 结论

本文研究了一种基于最优控制、预测校正以及强化学习的智能滑翔制导方法。首先引入了最优滑翔制导方法以满足终端经纬度、高度以及速度倾角约束；然后，针对终端速度大小控制问题，提出了基于侧向机动的速度控制策略，并综合考虑滑翔飞行特性与侧向机动飞行对终端速度进行了解析预测；最后建立了强化学习的框架模型，设计了状态空间、动作空间以及回报函数，采用Q-Learning对速度控制中的机动幅值进行智能调整，以保证终端速度控制精度。相对于传统的标准轨迹制导以及预测校正制导方法，智能滑翔制导的主要优点在于：

1)不依赖于标准轨迹，在飞行过程中根据当前飞行状态以及目标状态实时获得制导指令，具有极大灵活性，在无须人为调整制导参数的情况下仍能完成不同的制导任务；

2)采用强化学习对机动幅值进行智能调整，该方法无须离线建立样本库，计算效率高，适合于无法大量获得实际飞行数据且对实时性要求很高的飞行控制；

3)最优滑翔制导与终端速度预测均采用解析形式完成制导目标，Q-Learning计算效率高，并能够继承前期学习的优良经验，因此该策略计算量小，易于工程实现。