基于改进D-S证据理论的简支梁桥结构损伤识别

王先龙 刘建勋 张戎令，3 张文静 张新博

1.兰州交通大学土木工程学院，兰州 730070；2.甘肃省公路交通建设集团有限公司，兰州 730030；3.兰州交通大学道桥工程灾害防治技术国家地方联合工程实验室，兰州 730070

在结构损伤检测系统中，受自然环境、传感器自身精度等因素的影响，仅靠单一损伤指标很难精确地描述结构的损伤状态。因此，多种指标类型检测信息的融合成为结构损伤识别的研究热点［1-4］。D⁃S 证据理论作为广义贝叶斯理论，具有处理不确定信息的能力，在信息融合领域得到了较好的发展［5-8］。然而D⁃S证据理论在实际应用中存在不足之处，如面对高度冲突证据时可能得出与实际情况差别较大的结果［9］。这使得证据理论不能直接应用于存在较多冲突证据的信息融合中。

针对上述问题，国内外许多学者提出了解决方法。Smets［10］提出可传递置信模型（Transferable Belief Model，TBM），将冲突重新分配给未知的新命题，从而解决高度冲突证据问题。但此方法并不适用于识别框架已知的情况，并且在实际中证据完全可靠的条件并不易满足，使该模型的应用范围受到了限制。Yager［11］将冲突证据分配给全集，未冲突部分仍然按照Dempster 组合规则进行融合，有效解决了高冲突证据融合问题。该方法对证据的变化过于敏感且具有一票否决性，在证据较多时融合效果并不理想。Murphy［12］将证据的基本概率指派进行平均，然后使用Dempster 组合规则对新证据进行融合。试验结果表明，该方法能有效处理冲突证据，并且有较快的收敛速度。由于该方法未考虑各个证据的重要程度，融合结果不够合理。张欢等［13］利用皮尔逊相关系数计算证据之间的相关程度，根据相关程度确定证据体的权重。由于该算法只是对证据体进行加权，未考虑证据与焦元基本概率指派（Basic Probability Assignment，BPA）之间信任度不一致的情况，信息处理不够完全。邓勇等［14］通过各证据之间的距离计算证据的可信度，以此为权重对证据加权平均再进行融合。该方法融合过程收敛速度快，计算量适中，是目前较为有效的D⁃S 证据理论改进算法之一。虽然很多学者对D⁃S 证据理论的组合规则进行改进［15-18］且具有一定效果，但在实际工程中，证据冲突产生的主要原因是证据源受环境因素、人为因素的干扰、传感器精度等影响。因此，在证据融合前如何对证据进行修正处理才是解决高冲突证据融合的关键。

针对以上问题，本文引入灰色关联度理论和可信度概念，根据证据间的关联程度进行权重的分配，然后对原始证据的BPA 进行加权处理，再利用Dempster组合规则进行融合。

1 经典D-S证据理论及其缺陷

1.1 经典D-S证据理论

若θ是由N个相互独立命题组成的有限的完备集合，则称其为辨识框架，其幂集构成命题的集合为2θ。设m是识别框架θ的幂集2θ到区间［0，1］上的一个映射，A为识别框架中的一个或多个命题，如果满足：= 1，则称m为θ上的基本概率指派。m（A）为命题A的基本概率数，表示m对命题A的支持程度。若命题A满足m（A）＞0，则称A为θ上的一个焦元。

设m1和m2为两组基本概率指派，对应的焦元分别为Ai和Bj，则m1和m2组合后的新证据为

式中：k为冲突系数。

1.2 经典D-S证据理论的缺陷

在经典D⁃S 证据理论中，冲突系数k用来衡量证据焦元间的冲突程度，k越大则冲突越大。对于冲突较小的证据，D⁃S 组合规则可以得到较好的融合结果。对于高度冲突的证据，在使用过程中存在组合矛盾、一票否决和鲁棒性差三个问题。以某结构损伤为例对以上三个问题进行说明。分别从应力、挠度和基频数据得到三条证据（m1、m2、m3），损伤位置分别用a、b、c、d表示，见表1。由于挠度数据在采集过程中受外界干扰，导致m2与m1和m3有较大的冲突。

表1 损伤位置BPA

1）组合矛盾。主要表现形式：如果证据之间的冲突严重，直接使用Dempster 组合公式会产生违背常理的融合结果。对表1 中三条证据进行融合，融合结果为：m（d）=1，m（a）=m（b）=m（c）=0。三条证据对d损伤的支持度非常低，但Dempster 组合规则的融合结果将全部的信度分配给了d，这是不合理的。

2）一票否决。主要表现形式为：当某条证据对某个命题的支持度为0 时，无论其他证据对该命题的支持度多高，最后结果仍为0。表1 中m2（c）为0，即使m1（c）和m3（c）达到了0.766 9 和0.783 7，在融合结果中m（c）为0，与常理不符。

3）鲁棒性差。鲁棒性是反映当某个命题的基本概率指派发生微小变动时融合结果的变化幅度。将表1 中m2（a）减小0.001，m2（c）增加0.001，修改后的损伤位置BPA 见表2。融合结果为：m（c）= 0.996 5，m（d）=0.003 5，m（a）=m（b）=0。表2 仅将表1 中的证据m2进行微小调整，但融合结果相差极大，表明经典D⁃S证据理论鲁棒性很差。

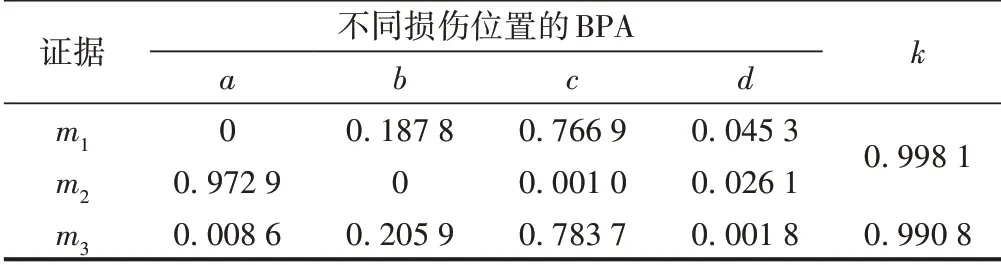
表2 修改后的损伤位置BPA

2 基于灰色关联度的改进D-S证据理论

在实际完备识别框架中，各证据不是相互独立的，应与其他证据有一定的关联性，因此不同证据对命题的评估应具有不同的权重。灰色关联度分析法是一种分析系统中各因素关联程度的方法，其实质是将研究对象影响因素的因子值视为一条线上的点，并与待识别对象影响因素的因子值所绘曲线进行比较，计算两者几何形状的接近程度，越接近则发展变化趋势越接近，关联度越大，以此来判断影响因素的主次，从而确定出权重。基于此，本文提出一种基于灰色关联度改进D⁃S 证据理论算法，通过各证据间的灰色关联系数确定其所占权重。一个证据与其他证据的灰色关联系数越大，则该证据受到其他证据的支持度就越大，具有较高的可信度，其权重就越高。具体算法流程如图1所示。

图1 本文算法流程

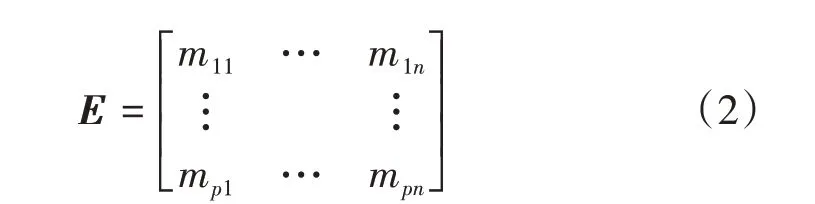
①假设辨识框架θ包含n个元素，p条证据，其对应的p×n矩阵表示为证据序列矩阵（Evidence Sequence Matrix，ESM），用E表示，即

设参考证据为mj=｛mj（g），g= 1，2，… ，n｝（j=1，2，…，p），比较证据为mi=｛mi（g），g=1，2，…，n｝（i=1，2，… ，p），则证据mi和mj之间的关联系数可表示为

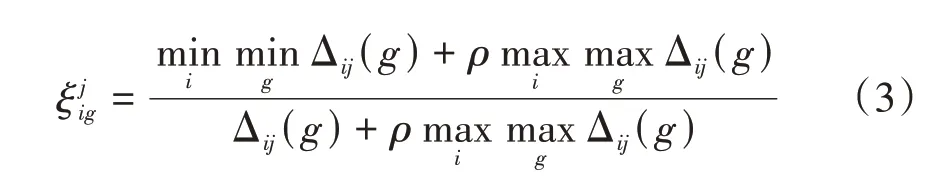
式 中：Δij(g) =|mi(g) -mj(g)|；ρ为 分 辨 系 数，ρ∈(0，1)，一般ρ= 0.5。

通过计算参考证据mj所有的关联系数，得到证据mj的灰色关联系数矩阵（Gray Correlation Coefficient Matrix，GCCM），用G表示，即

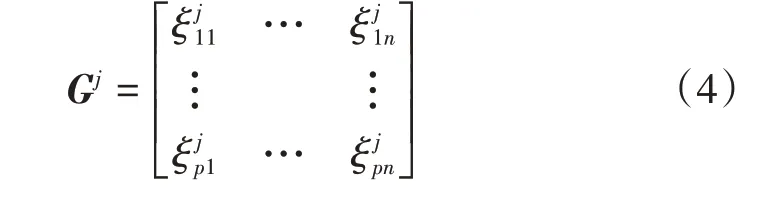
②对辨识框架内所有证据进行关联系数计算，并将证据之间的关联系数作为支持度，得到支持度矩阵为

③由于灰色关联系数计算了p条证据之间所有元素的关联系数，当一个信息源出现故障时，与其他正常证据源获得的证据相比，该信息源收集的证据往往具有较小的灰色关联系数。因此，基于灰色关联系数矩阵定义评判标准Ti来识别故障信息源，即

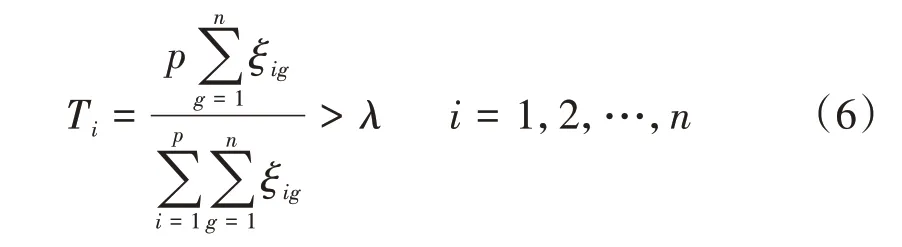
式中：λ为阈值，其值越小，对应信息源的故障率越大，一般λ=0.85。

当Ti＜λ时，说明第i个信息源不可靠，其支持度应为0。此时，得到修正故障信息源的证据支持度矩阵S*。

④将新的支持度矩阵S*经归一化处理后得到证据可信度Ci，即

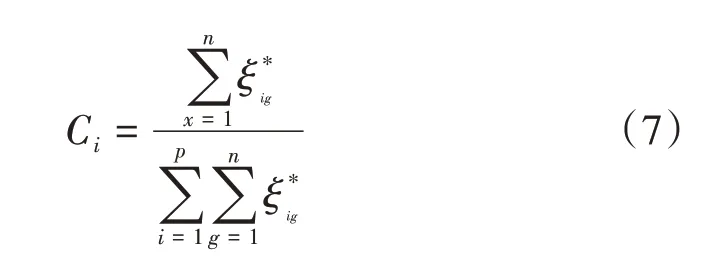
⑤将可信度Ci作为证据mi的权重对原始BPA 进行加权处理，定义加权后的BPA为m*，即

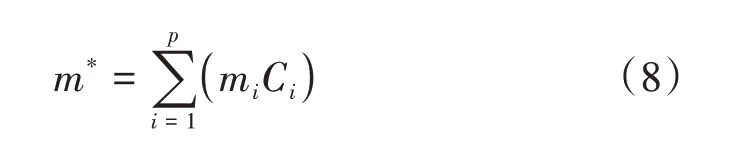
⑥采用Dempster 组合规则将加权后的新证据自身融合两次，得到最终的融合结果。

3 算例分析

3.1 经典D-S证据理论缺陷的解决

将表1 中的证据按照本文改进算法进行证据融合，融合结果为：m（a）= 0.102 2，m（b）=0.003 7，m（c）=0.894 0，m（d）=0.000 1。其中，指向c损伤的概率最大，与1.2节中的分析一致，表明本文提出的改进算法很好地解决了经典D⁃S证据理论中的组合矛盾和一票否决问题。

将表2 中的证据进行证据融合，融合结果为：m（a）= 0.080 1，m（b）= 0.003 8，m（c）= 0.916 0，m（d）=0.000 1。

对比本节两组融合结果可知，对于基本概率指派的微小扰动，融合结果的变化幅度也是微小的。随着m2（c）的增大，m（c）增大，m2（a）减小，m（a）亦减小，说明基本概率指派和组合结果的变化是同步的，本文提出的改进算法拥有较强的鲁棒性。

3.2 多证据融合比较

证据的数量是影响融合效果的重要因素之一，不同数量证据融合结果的合理性是衡量融合方法优劣的一个重要角度。本文选择文献［13］的数据（表3）与经典D⁃S证据理论、文献［11］、文献［12］和文献［13］进行对比分析。

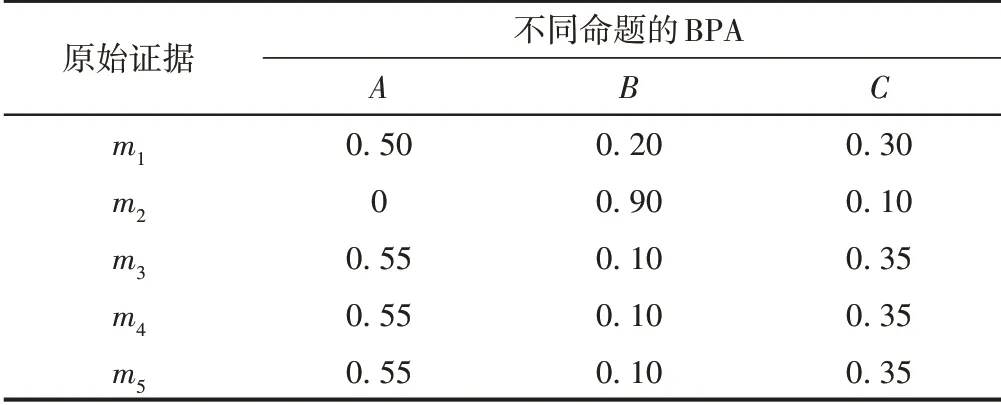
表3 五条原始证据BPA

将表3 中的5 条证据分为4 组，分别是第1 组（m1、m2），第2 组（m1、m2、m3），第3 组（m1、m2、m3、m4）和第4组（m1、m2、m3、m4、m5）。由于m2对命题B有较大的支持度，所以仅对第1组证据进行融合，其结果应偏向于信任命题B。随着证据数量的增加，命题A的支持度不断上升，由此推断m2犯错的可能性极大，所以在4 组证据的融合过程中，m（A）应逐渐增大，m（B）应逐渐减小。4组证据支持的命题应为BAAA。分别将4组证据进行融合，结果见表4。

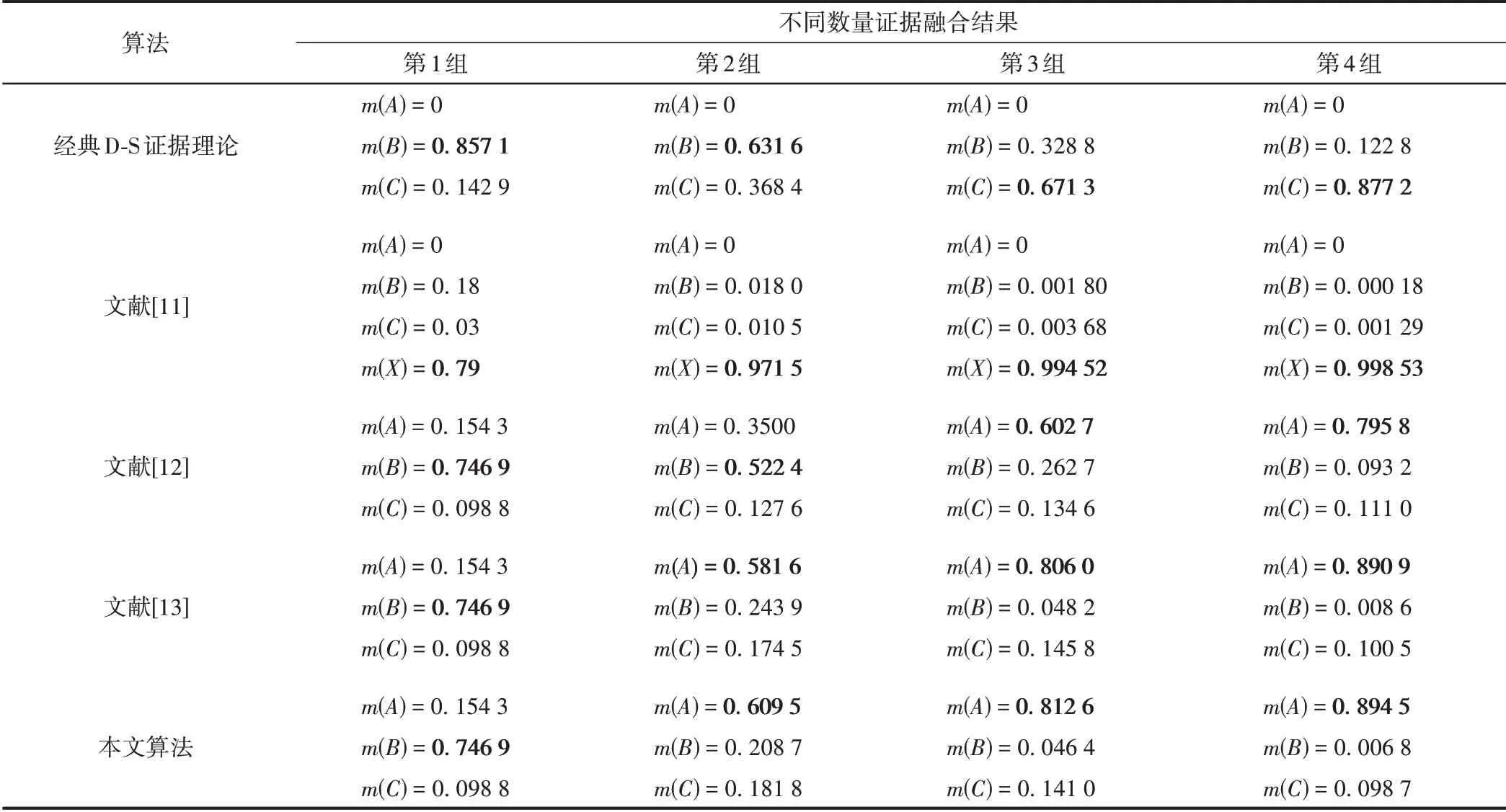
表4 不同数量证据融合结果对比

由表4 可知，经典D⁃S 证据理论对高冲突证据无法进行有效处理，在融合结果中m（A）始终为0。这是由经典D⁃S 证据理论的一票否决问题所导致的，尽管后来所有证据都支持命题A，但m2否定了命题A，导致m（A）始终为0，融合失败。文献［11］将冲突分配给全集m（X）的方式并未发挥很大作用，无论证据数量是多少，这种算法都将绝大部分的基本概率指派分配给全集m（X），未识别出合理命题。相比之下，文献［12］、文献［13］和本文算法都能有效识别出合理命题B。其中，文献［12］由于未考虑证据之间的关联性，在第2 组增加m3的情况下仍未发现m2的错误，直到第3组支持命题A的m4出现才能有效识别目标。文献［13］和本文算法都取得了与分析一致的融合结果，但本文算法在命题信任度和收敛速度上都优于文献［13］。

为了比较本文算法与经典D⁃S证据理论及其他改进算法对合理命题的反应速度，将4 组证据对应合理命题的融合结果进行对比，见图2。可知，本文算法对合理命题的融合基本概率都优于经典D⁃S证据理论及其他改进算法。

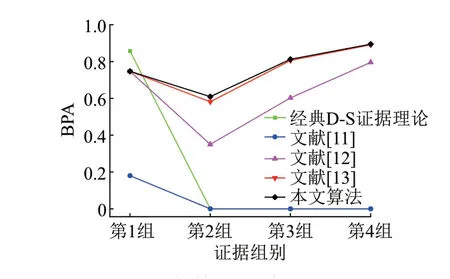
图2 各算法融合结果比较

3.3 数值模拟

为了检验本文算法在工程中的适用性，使用MIDAS/Civil建立一个长度为10 m、两端固结的钢梁有限元模型，划分为10 个单元，横截面尺寸为350 mm×500 mm，钢梁中部作用P=1 000 kN的荷载，见图3。

图3 钢梁有限元模型离散图

以单元弹性模量降低来模拟结构损伤，弹性模量降低百分比为结构损伤程度，每个结构单元包括5 种工况：无损、损伤20%、损伤40%、损伤60%、损伤80%。选取结构单元的特性指标应力、挠度和结构基频进行融合，以确定结构的损伤位置和损伤程度。计算钢梁在无损及损伤20%、40%、60%、80%共41 个工况的特征指标。考虑到实际工程中环境因素对结构的影响，分别以单元应力和挠度的±5%、结构基频的±2%进行样本随机扩展，每种指标的样本扩展数为10，最终得到样本总数为451。随机选取样本数的90%为训练样本、10%为测试样本，相应样本数分别为406和45。

使用以上训练样本对融合模型进行训练，生成BPA的高斯型隶属度函数为

首先将训练样本带入式（9），生成各工况对应特征指标的隶属度函数。然后将测试样本与各指标对应的隶属度函数进行匹配，得到测试样本与各指标的匹配程度，生成测试样本的BPA。最后，用本文算法对生成的BPA 进行融合计算，得到钢梁的损伤情况，计算结果见表5。可知，以单个单元的特征指标数据来识别钢梁损伤准确率均在91%以上；以两个单元识别的准确率均在95%以上；以三个单元识别的准确率均为100%。说明在本文算法中，仅以单个单元的应力和挠度及钢梁的基频，就可以较为准确地判断出钢梁的损伤情况，两个单元的识别准确率略有提高，三个单元完全可以识别出钢梁的损伤情况。

表5 融合结果识别准确率

4 结论

1）考虑证据间的关联性可以有效避免错误证据的干扰，提高融合结果的准确率。

2）改进后的算法能有效解决经典D⁃S证据理论面对高冲突证据时存在的组合矛盾、一票否决、鲁棒性差等问题。

3）通过灰色关联度矩阵定义的评判标准可准确识别出故障信息源，对故障信息源收集的证据进行归零处理，可明显提高融合结果的准确率。与其他改进算法相比，本文算法在不同多个证据上的融合结果都表现出更高的命题信任度。

4）通过对钢梁结构损伤的模拟计算，验证了本文算法可以应用于结构的损伤识别，并具有精确的识别结果。与单一指标损伤识别相比，在对结构损伤位置和损伤程度的识别过程中，本文算法的识别结果更准确可靠。

5）本文算法能有效解决经典D⁃S证据理论存在的高冲突证据问题，具有较高的识别效率和收敛速度，可以准确识别结构损伤情况。