基于可拓物元法的轨道交通换乘站服务水平综合评价
2022-08-05赵晓磊肖为周
赵晓磊,肖为周
(苏州大学轨道交通学院,江苏苏州 215000)
地铁作为具有专有路权的公共交通方式,因准时、绿色、安全、高效等优点,逐渐成为大城市解决交通需求问题的重要手段。而车站作为地铁集散客流的节点,其内部服务水平会影响乘客的整体出行体验,因此建立合理的综合服务水平评价方法来反映站内行人服务水平,对车站运营者制定客流组织方案、提升乘客出行品质有重要意义。
国内外对于轨道交通车站行人服务水平评价研究已经取得了一定成果。FRUIN[1]最早将服务水平概念引入交通枢纽站点,用密度、速度等行人特性指标描述区域拥挤程度,将服务水平分为A~F级。任美君等[2]深入研究换乘站的换乘设施,对每个换乘设施设计了多个指标并根据调查数据进行分级,用加权法得到换乘设施的综合服务水平。周慧娟等[3]针对乘客乘车的具体环节设计指标集,然后通过重要性调查的统计结果筛选关键指标,建立基于出行全过程的服务水平评价体系。文献[4—7]分别用雷达图法、多变量回归法、物元法、粗集多属性决策等方法对服务水平进行评价。然而上述对行人服务水平的综合评价中,部分指标没有考虑时间因素的影响,常用的最大密度、平均密度等无法较好地描述一段评价时间内的整体情况,因此建立能够评估诸如早高峰、晚高峰时段内整体车站服务水平的方法,定量比较不同客流组织策略对高峰期服务水平的影响效果,对于车站运营有重要意义。
本文利用现有研究的指标分级标准及方法,在指标体系中引入低服务水平时间指标,使用可拓物元法建立某时段站内行人服务水平的综合评价模型,为车站管理者制定组织措施提供参考。
1 换乘站服务水平指标体系与权重确定
1.1 低服务水平时间指标
综合评价的指标体系一般由时间类指标、密度类指标与比例系数类指标构成,密度人数类指标的选取通常为最大密度或平均密度,最大密度只能反映某时刻的密度评价且一定程度上会夸大最终结果,平均密度则无法体现周期性变化的客流密度特点。车站实际的密度服务水平每分每秒都在变化,这类指标难以较好地描述评价时段内行人密度服务水平的情况,因此本文采用低服务水平时间指标对区域拥挤度进行评估。
低服务水平时间是指某设施处于低服务水平的持续时间,通过设定一个低服务水平阈值,累计评价时段内设施密度或人数超过了阈值的时刻。阈值可以基于现有密度分级或按需求设定。
(1)
(2)
式中:tlow,ti表示低服务水平时间以及第i秒是否为低服务水平的0~1变量,ρlow,ρi表示低服务水平阈值及第i秒的指标数值。
使用区域低服务水平时间指标替换常用的密度类指标,弥补密度类指标未考虑时间因素的缺点,以此来表现评价时段内车站某区域的拥挤情况。
1.2 评价指标体系
换乘站内行人的体验由多部分组成。本文参考已有研究对评价指标体系的研究及构建方法[8-9],经过指标初选、主客观结合的二次筛选过程,从基本出行体验、走行体验及设备设施体验3方面来反映行人在站内的体验,建立评价指标体系,如表1所示。基本出行体验反映的是乘客达成站内出行目标的便捷程度,走行体验与设备设施体验则是走行与设备使用部分的情况。指标名称后为对应编号。
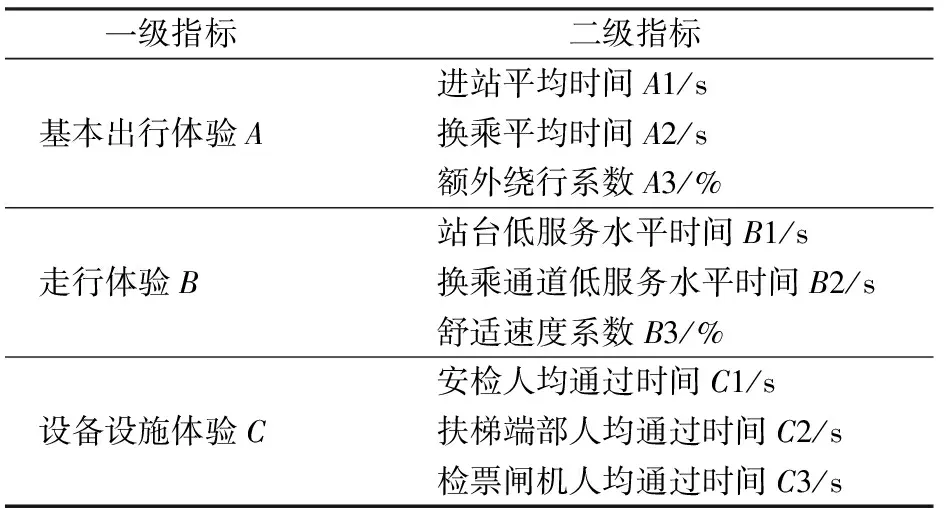
表1 地铁换乘站服务水平综合评价指标体系
1.3 权重确定
本文采用层次分析法确定各组指标的权重。通过乘客问卷调查搜集各组指标的判断矩阵并进行一致性检验,选取有效判断矩阵,采用方根法计算权重结果,取同类矩阵权重均值作为最终结果[10-11]。
2 可拓物元评价法
可拓物元法可以兼容多层级、多组合的指标之间的关系并进行综合计算,从而能够对较为复杂、不易直接描述的问题进行分析。物元的概念最早是由广东工业大学的蔡文等[12]提出,其具体定义为若事物N存在一系列特征C,对应各个特征的量值为V,那么三者组成的矩阵R=(N,C,V)就称为物元[13]。假设特征及对应量值有n个,那么矩阵如式3所示:
(3)
2.1 物元的建立
可拓物元法即是将问题分为若干个物元进行描述。对于服务水平综合评价来说,根据建立的指标体系,物元R=(N,C,V)内,N为待评价的各个站内体验;ci(i=1,2,…,n)为站内体验对应的具体指标;vi(i=1,2,…,n)则为指标ci所对应的量值,根据物元类型的不同,可以是具体数值或数值区间。
2.2 经典域与节域的确定
假设将指标的评价等级分为y级,那么每个评价等级下的指标都会对应不同的数值变化范围,根据可拓理论,即可建立各评价等级下的经典域物元Rj=(Nj,C,Vj),具体如式(4)所示:
(4)
式中:Rj表示在j(j=1,2,…,y)评价等级下的经典域物元矩阵;Nj表示j等级下影响综合服务水平的待评价体验;Vj为j评价等级下各指标的取值范围;aij与bij(i=1,2,…,n)分别是j评价等级下,指标ci对应数值区间的下界和上界。
由此可知,经典域即是在不同评价等级下各指标的对应区间。当把指标所有经典域范围合并,得到的就是节域,节域物元矩阵Rp如式(5)所示:
(5)
式中:aip与bip(i=1,2,…,n)为指标ci所有经典域范围合并后的下界与上界。
2.3 待评价物元的确定
待评价物元是指由待评价对象的具体量值组成的物元,其各个特征指标的量值是确定的。其矩阵形式如式(6)所示:
(6)
待评价物元Rm中,N同上文,为各待评价的一级指标;ci(i=1,2,…,n)为某一级指标下的二级指标;vim表示二级指标ci的具体数值。
2.4 计算关联度矩阵
可拓物元法是通过关联度矩阵来描述事物评价的。在收集到事物的一组待评价数据后,通过关联函数计算关联度矩阵。假设有指标数值vim与经典域区间vij=(aij,bij),定义vim与vij之间的接近度ρ(vim,vij)的计算方式如式(7)所示:
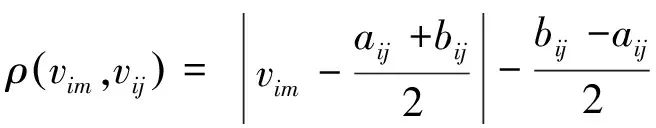
(7)
指标值与节域得到接近度计算方式类似,如式(8)所示。
(8)
得到接近度之后,再进一步计算得到指标值vim与各个评价等级经典域之间的关联度kj(vim),具体计算如式(9)所示。
(9)
式中:|vij|表示该数值区间的长度。指标值与各经典域的关联度kj(vim)(j=1,2,…,y)所组成的矩阵K(vim)=(kj)1×y,即为该指标的关联度矩阵。
2.5 综合关联度及评价结果确定
计算得到所有最下层指标的关联度矩阵后,就可以结合同组指标的权重,逐级向上计算得到上一层指标的综合关联度矩阵Z=(zj)1×y,假设λi为第i个指标的权重,zj计算方式如式(10)所示:
(10)
式中:zj表示上一级指标对评价等级j的关联度。最终计算得到最上层对象的评价等级关联度矩阵。根据最大关联度原则,关联度矩阵中最大值所对应的评价等级j'就是该指标的评价结果。
3 案例分析
为了实现对不同客流组织场景的模拟与数据收集,在比较常用仿真手段后[14],选择Anylogic仿真软件,并分析车站具体问题,提出多个客流组织场景,分别对不同组织措施场景进行仿真,收集指标数据,进行服务水平综合评价与分析。
3.1 苏州地铁石湖东路站
石湖东路站是苏州地铁2号线与4号线的换乘站,主体位于东吴南路与石湖东路交叉口下,车站为地下三层岛式车站,整体呈倒T型。两线共用站厅在B1层,共6个出入口;东西向的2号线及其站台位于B2层,南北向的4号线及站台位于B3层,在T字节点处采用楼梯直连站台的换乘方式,两线站台的相对位置如图1所示。
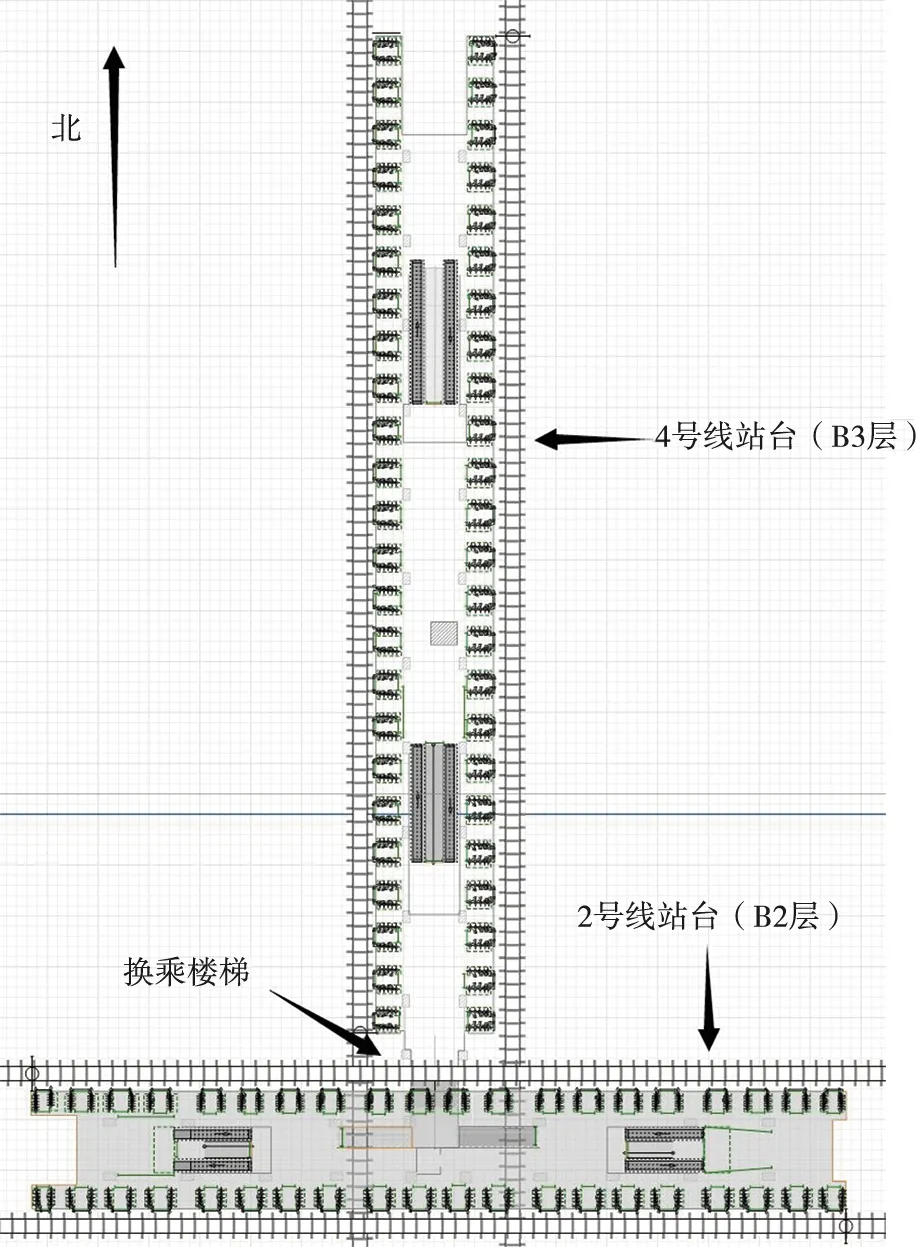
图1 两线站台位置Fig.1 Platform location of two lines
目前换乘组织具体如图2所示。图内为T字节点处的换乘通道,下层为4号线站台,连接的上层为2号线站台。现行措施将T型通道中间隔开,形成2个单向L型通道,4号线换乘2号线的乘客与2号线换乘4号线的乘客各使用其中一条。
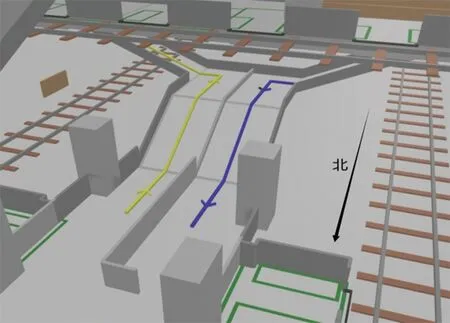
图2 换乘流线现状Fig.2 Transfer streamline status
石湖东路站的早高峰通勤客流非常突出,主要为换乘客流,因此仿真时段设置为早高峰7:00—9:00。
总体研究流程主要分为仿真数据搜集与处理、仿真模型构建与仿真结果评价3部分,如图3所示。
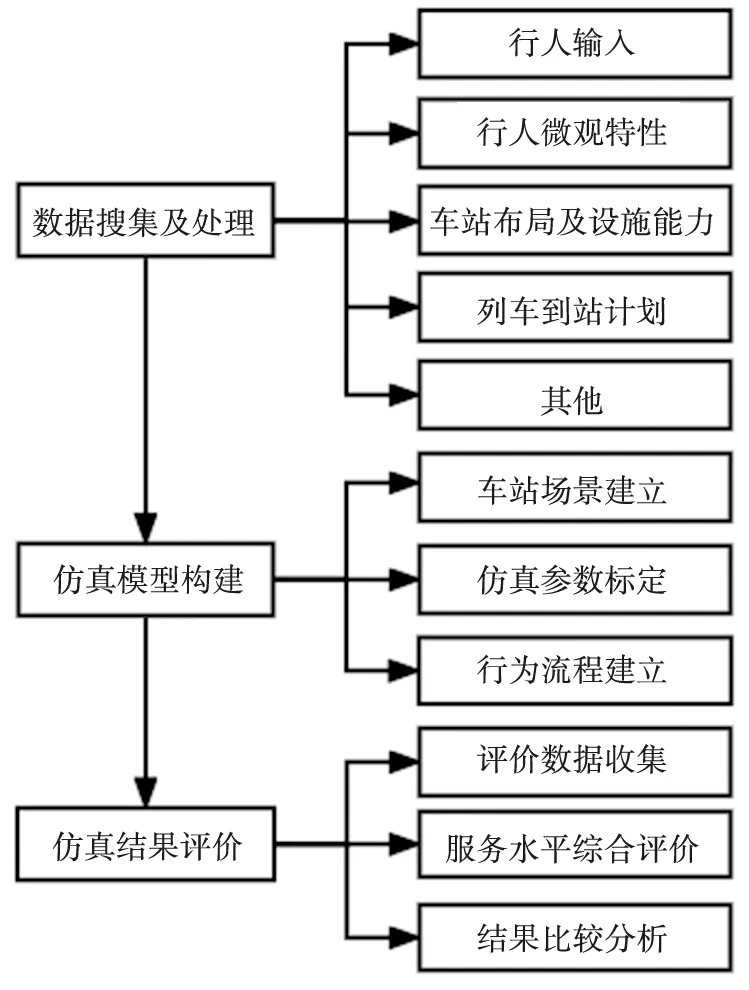
图3 研究流程Fig.3 Research process
3.2 基本参数设置
仿真参数部分主要通过调查数据得到。部分参数如表2所示,行人舒适速度服从正态分布,安检及售票机服务时间服从均匀分布,闸机服务时间服从对数正态分布。
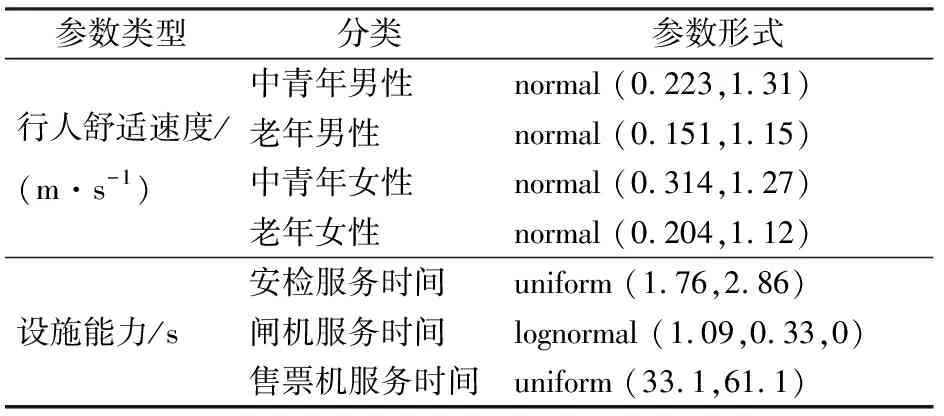
表2 石湖东路站仿真部分参数
列车运行计划、站内客流群体的性别比例、年龄段比例等数据则根据石湖东路站早高峰具体调研结果与进行设定。行人输入、站内线路分流比例等则结合AFC数据与全网站间OD数据在仿真软件内进行详细设定。
3.3 场景设定及仿真结果
根据现状客流组织与客流数据,对石湖东路站进行仿真,根据E级密度分级,设定热力图关键密度为3.33人/m2。现状仿真8:10的密度热力图如图4所示,现状指标值如表3所示。
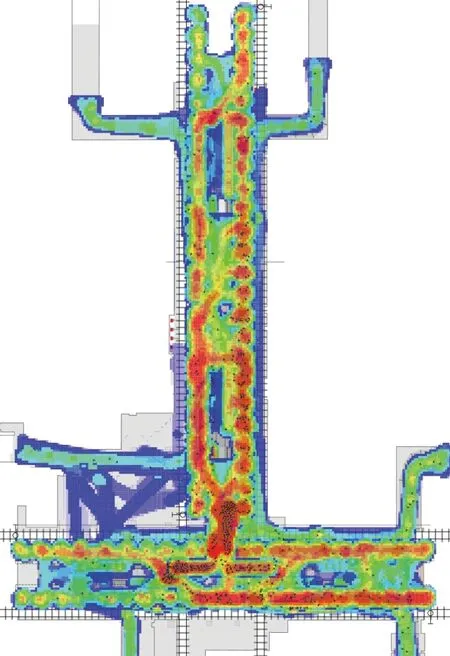
图4 现状车站8:10密度热力图Fig.4 Current density heatmap at 8:10
由于换乘通道狭小,且4号线换乘2号线方向与2号线换乘4号线方向皆存在较大的换乘客流,即使隔开通道,T字节点处的拥挤情况也非常严重。并且由于通道分隔,4号线换乘2号线的客流从东侧通道(图1黄色路线)流动,该方向换乘量极大,导致大量乘客从2号线站台的东部进入;同时,根据车站出入口进站客流的调查情况,乘坐2号线的进站客流主体也由2号线东部楼扶梯下行至站台,导致2号线站台东部候车密度明显较高,根据高峰期观察,2号线下行方向东侧站台平均队列排队人数9.5人,西侧6.5人,东侧偶尔出现乘客滞留。针对上述问题,本文建议交换图1中的换乘客流方向,同时对部分换乘客流进行引导,使其从站厅进行换乘,从而缓解通道压力。由此设计以下场景。
场景1:交换通道内客流方向,分流4号线北侧部分换乘乘客先返回上层站厅,再通过站厅换乘。
场景2:交换通道内客流方向,分流2号线部分换乘乘客先返回站厅,再通过站厅换乘。
场景3:交换通道内客流方向,并同时分流4号线与2号线的部分换乘乘客由站厅换乘。
场景4:只交换通道内客流方向。
根据权重问卷调查时对乘客的换乘分流意愿询问,4号线站台上的被调查者中有25.8%愿意从站厅换乘,2号线站台上的被调查者则为16.7%,以此设定高峰期站厅分流概率。对4种场景分别进行仿真,所得指标数据如表3所示。
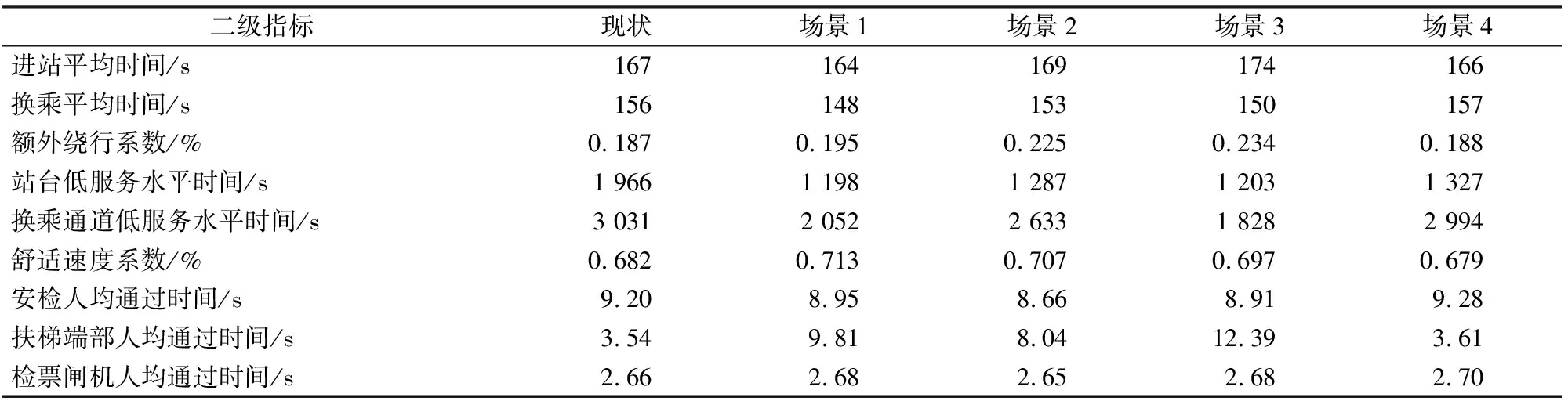
表3 石湖东路站各组织场景仿真指标结果
3.4 场景评价结果及分析
本文拟将指标分为优、良、一般、较差与差5个等级。额外绕行系数、舒适速度系数的分级设置参考赵栋煜[8]的研究。设备设施体验下的二级指标,采用丁佳麒[15]的方法,通过K均值聚类对服务时间样本进行4个聚类中心的聚类分析,结合样本范围确定5个评价分级,如表4所示。
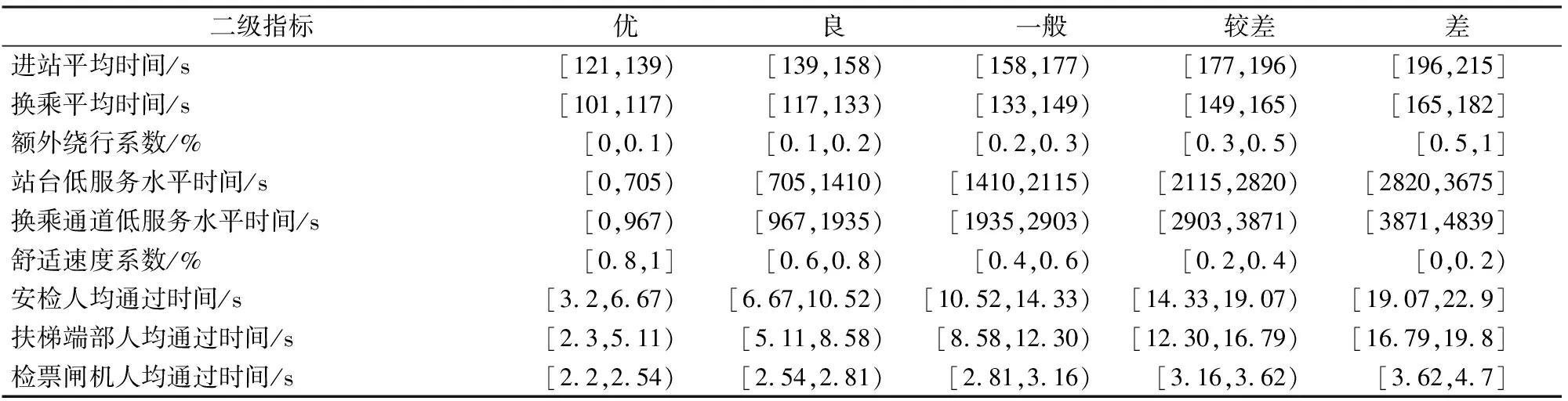
表4 综合评价二级指标分级
进站平均时间与换乘平均时间,通过在平峰期与高峰期分别进行跟踪调查,记录每条流线若干时间样本,取平峰期各流线均值,并利用各流线客流比例计算加权平均值作为指标值下限,高峰期为上限,并将区间范围划分为5个等级。
低服务水平时间指标的分级,在密度阈值设定方面,采用任美君等[2]以苏州轨道交通换乘站数据为基础的设施密度分级结果,将站台候车区与换乘通道到达E级时密度阈值作为低服务水平判定阈值。指标本身的分级主要考虑低服务水平时间可能的上限,站台候车区与换乘通道的客流量是随列车到发周期变化的,本文记录车站7:00—9:00时段内换乘通道的总使用时间作为上限,并使用视频拍摄方式,统计高峰期站台候车区从清空至到达E级密度人数的平均积蓄时间,结合列车到站计划,计算评价时段内候车区的拥挤时间上限,以低服务水平时间为0,即理想情况为下限。根据层次分析法得到的权重值组合如表5所示。
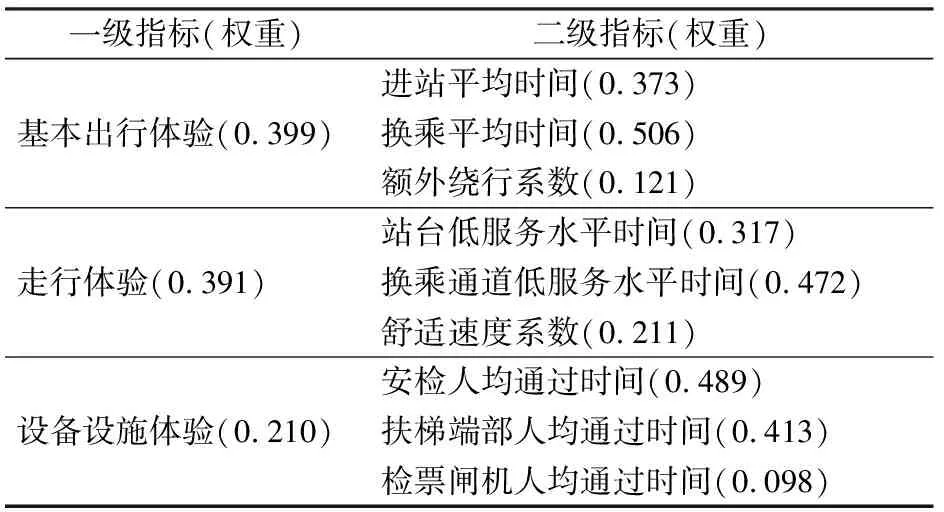
表5 评价指标体系权重
根据5个场景的实际指标值、分级与指标权重,利用可拓物元法,计算综合服务水平关联度。以现状场景下,一级指标基本出行体验指标A为例,待评价物元如式(11)RAm所示,表示对应二级指标组合的待评价值:

(11)
确定基本出行体验指标A的节域RAp,以及各评价等级对应的经典域,以优等级为例,如式(12)和式(13)所示:

(12)
(13)
节域与经典域在形式上相似,节域物元内的数值范围是二级指标所有评价等级数值范围的并集,而经典域物元的数值范围则是对应评价等级下的指标值变化范围。接着,利用计算式(7)—(9)计算待评价物元RAm与各级经典域物元的关联度矩阵KA11-A13如式(14)所示:
(14)
KA=wA11-A13×KA11-A13。
(15)
由此可以得到:
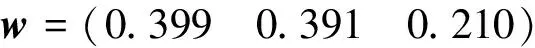
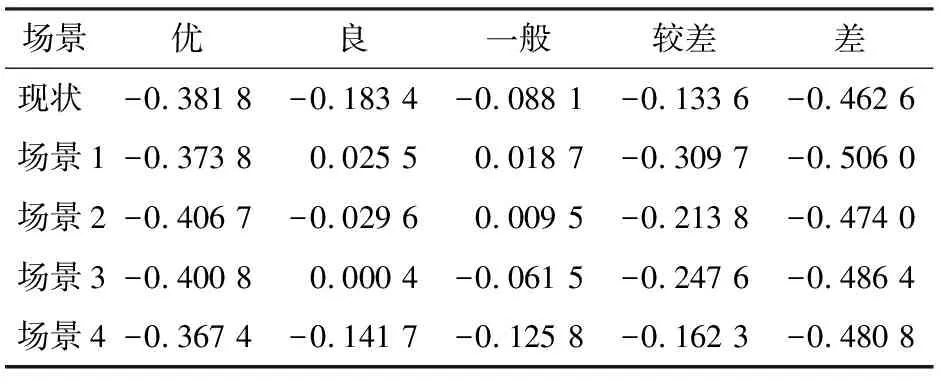
表6 各场景综合服务水平关联度计算结果
根据最大关联度原则,各场景综合评价结果如表7所示。
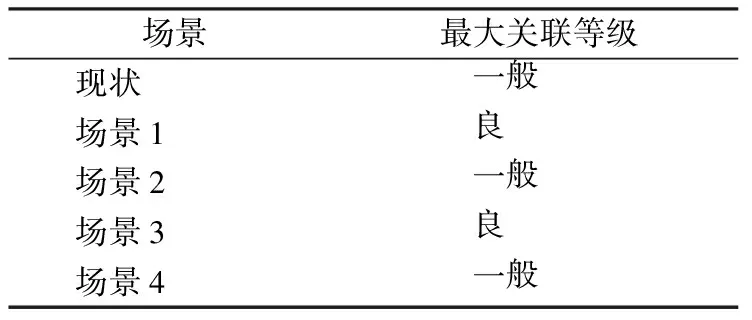
表7 行人综合服务水平评价等级结果
根据关联等级结果可知,场景1与场景3评价最好。将两类场景的具体指标列表如表8所示。表中编号所代表的具体指标可由表1得到。

表8 场景1、场景3指标对比
场景3是在场景1的基础上,增加“对2号线的换乘乘客进行站厅分流”这一措施。此举进一步缓解了换乘通道的拥挤情况,但由于2号线换乘量规模小于4号线,同时2号线换乘乘客绕行意愿不强,在不改变分流比例的情况下,换乘通道拥挤时间下降幅度已减缓,降幅约10%左右。然而另一方面,两线同时分流使得站厅客流量短时明显增加,流线冲突明显,影响了进站乘客效率、舒适速度的保持、极大增加了额外绕行,并且导致楼扶梯口的人均通过时间明显增加。从客流引导实施角度来看,需要实行的措施也是越少越好。因此,采取场景1的方式,在实施难度相对简单的情况下,能够提高车站早高峰的综合服务水平。场景1的密度热力图如图5所示,与现状相比,换乘节点与候车区的高密度情况有所改善。
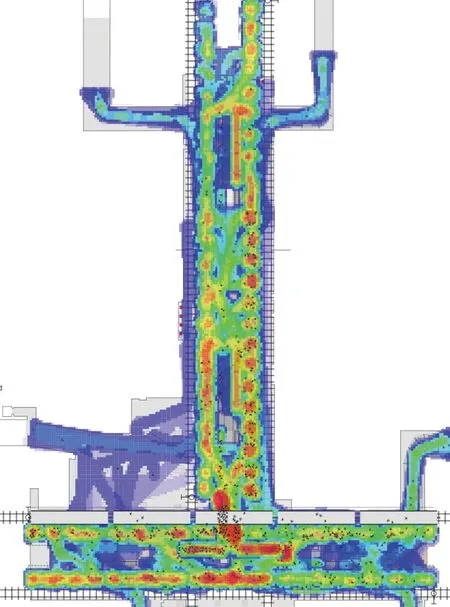
图5 场景1车站8:10密度热力图Fig.5 Scenario 1 8:10 density heatmap
4 结 语
本文建立地铁换乘站服务水平综合评价模型,对多种客流组织方案进行仿真、评价与分析。
1)考虑密度类指标的时间因素,引入低服务水平时间来描述评价时间段内的拥挤情况,从基本出行、走行与设施设备3方面体验建立指标体系。通过层次分析法确定权重,采用可拓物元法评价时段的服务水平。
2)以苏州地铁石湖东路站为研究对象,结合仿真得到不同组织场景下的各项指标,分析不同场景的服务水平评价结果,以此确定最佳的客流组织方案,为车站管理者制定与抉择客流组织方案提供技术支撑。
最后,本文通过仿真得到客流数据,与实际情况存在一定误差,此外评价未考虑乘客主观感受,指标体系没有做到主客观统一。后续将对体系的构建过程与物元模型的计算做进一步研究。
