基于麻雀搜索算法的橡胶复合挤出机温度压力解耦控制
2022-08-05尚亚强严一踔丘军意谷龙强陈明霞
王 冰 尚亚强 严一踔 丘军意 谷龙强 陈明霞
基于麻雀搜索算法的橡胶复合挤出机温度压力解耦控制
王 冰 尚亚强 严一踔 丘军意 谷龙强 陈明霞
(桂林理工大学机械与控制工程学院,广西桂林 541006)
橡胶挤出机是橡胶制品生产的关键设备,其挤出过程是一个多变量大时滞系统,其中温度和压力两个关键的工艺参数存在强耦合,单变量控制和传统的解耦方式无法保证挤出制品质量。文章从影响橡胶复合挤出机生产过程中的众多因素中选出最重要的两个因素,即温度和压力来进行研究。针对橡胶复合挤出机温度和压力的耦合现象,使用麻雀搜索算法(Sparrow Search Algorithm,SSA)对PID神经元网络的初始权值进行优化以及调整,以加快系统解耦后的响应速度和提高系统稳定性。利用MTATLAB软件分别使用PID神经元网络和SSA-PID神经元网络对挤出机温度压力进行解耦控制,并将二者结果对比。结果表明,SSA- PID神经元网络的解耦控制后的系统响应速度更快、稳态误差更小,系统的动态性能和稳态性能都有所提升。
橡胶复合挤出机;麻雀搜索算法;PID神经网络;解耦控制系统
引言
橡胶挤出机又称压出机,是橡胶制品生产中重要的工艺设备之一[1]。挤出机温度控制是决定挤出机挤出物料质量的关键环节。如果熔体胶料温度过高,会引发胶料焦烧现象,而温度过低,会造成熔体流动性差。在实际生产过程中,室温、加热器功率、静液压功率以及冷却水温度等都会对熔体温度产生影响。同时压力也是重要的工艺参数,决定着挤出机的产量。而机头压力又受到熔融历程和机筒温度等因素影响。而螺杆转速和熔体温度波动都会引起熔体压力变化。可见,挤出机挤出成型过程中的温度和压力是耦合在一起的,因此,研究挤出过程中熔体的温度和压力的解耦控制是很有必要的[2]。
目前,使用传统PID解耦控制无法满足挤出机复杂的工业环境,因此需要一种新的解耦方式来适应新的橡胶生产工业,所以本文提出了一种基于麻雀搜索算法优化的PID神经元网络解耦控制。利用初始权值对PID神经元网络的影响,将麻雀搜索算法收敛速度快、精度高的特点运用到对初始权值的优化,实现对系统更优的解耦控制。
1 挤出机温度压力控制系统简介
1.1 工艺流程简介
挤出成型装置主要由挤出机、挤出机的控制系统和辅机组成,作为关键环节的挤出机,主要包含传动系统、加热冷却系、统挤压系统以及机头口型,辅机设备是满足工艺要求的机器,而控制系统主要是由电器设备以及各类元器件构成。
挤压系统的作用是将高弹性状态的橡胶向前推,使其变成粘性状态的熔体,然后挤出成半成品。驱动系统为螺杆提供不同的扭矩和旋转速度。加热冷却系统主要用于对挤出系统和挤出机头进行加热或冷却,使其达到工艺设定要求各个部位的温度。机头位于料筒前端,用于改变胶料的运动状态,很大程度上影响基础质量。口型决定橡胶半成品的形状和尺寸,可以通过改变一台挤出机的口型来改变橡胶半成品的形状。控制系统依据自身智能化的程度,通过电气仪表以及执行机构来控制挤出机的各个部位,并检测各个部位的温度、压力和流量,来控制挤出成型设备的整体运行状况,实现对挤出生产线的全线控制[3]。
根据胶料在挤出机中的变化,可以将螺杆工作部分按其作用大致分为喂料段、压缩段和挤出段三个阶段[4]。根据胶料在挤出机中的变化将螺杆工作部分制作为流程图,如图1所示。
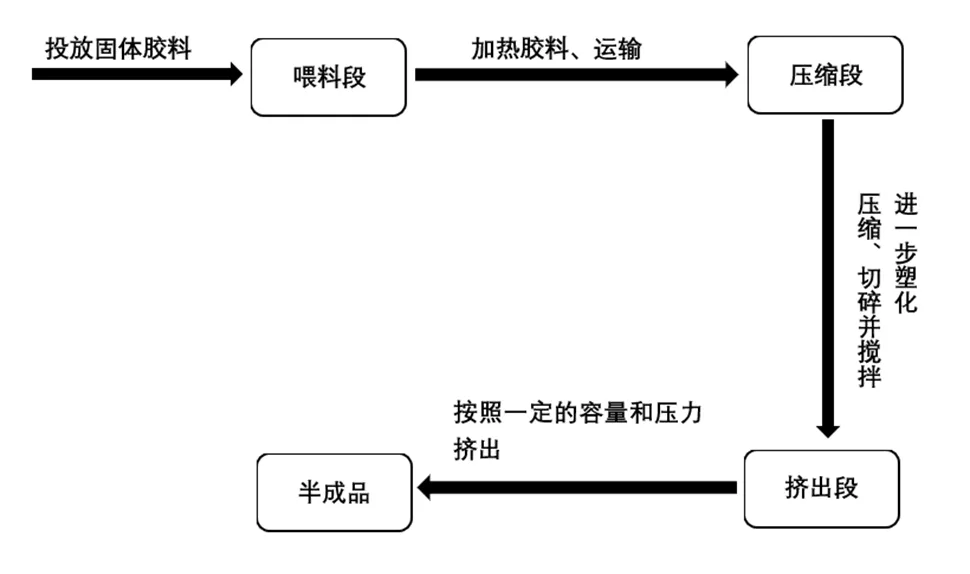
图1 螺杆工作部分制流程图
1.2 挤出机温度压力的双变量耦合系统
挤出工艺条件直接影响复合挤出机挤出胎面质量,温度、螺杆转速和挤出速率等都对挤出工艺有一定的影响[5]。陈明霞[2]对挤出机温度压力控制系统建模进行分析,针对熔体温度与熔体压力的耦合关系,通过MATLAB软件借助实验测得数据量对于传递函数模型进行辨识计算得出熔体温度T和机头压力P关于机头加热器功率W及螺杆转速n的关系式。
熔体温度T关于机头加热器功率W的传递函数为:
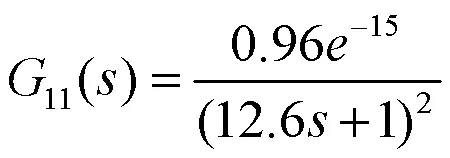
熔体温度T关于螺杆转速n的传递函数:
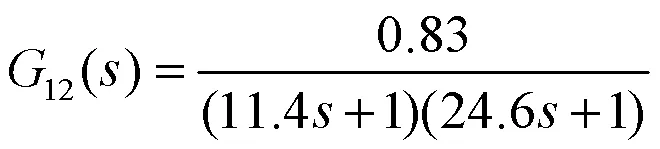
熔体压力P关于机头加热器功率W的传递函数:
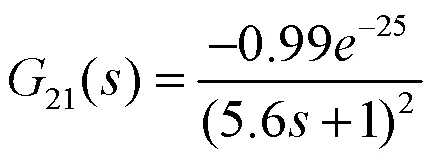
熔体压力P关于螺杆转速n的传递函数:
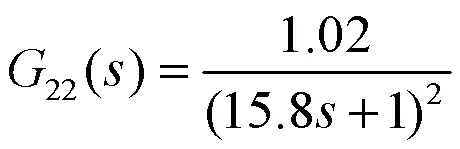
挤出机温度压力系统的传递函数矩阵为:
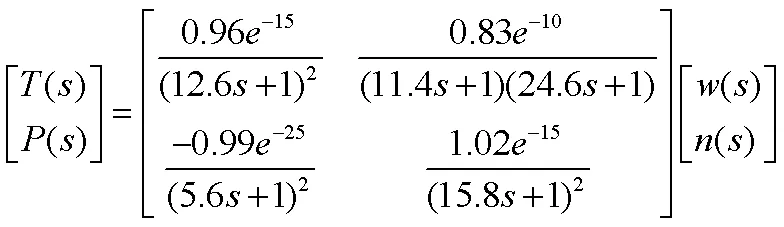
挤出机温度压力的双变量静态耦合系统如图2所示。
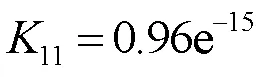
根据以上传递函数可以在MATLAB的Simulink模块搭建挤出机的温度压力双变量耦合系统模型,如图3所示。
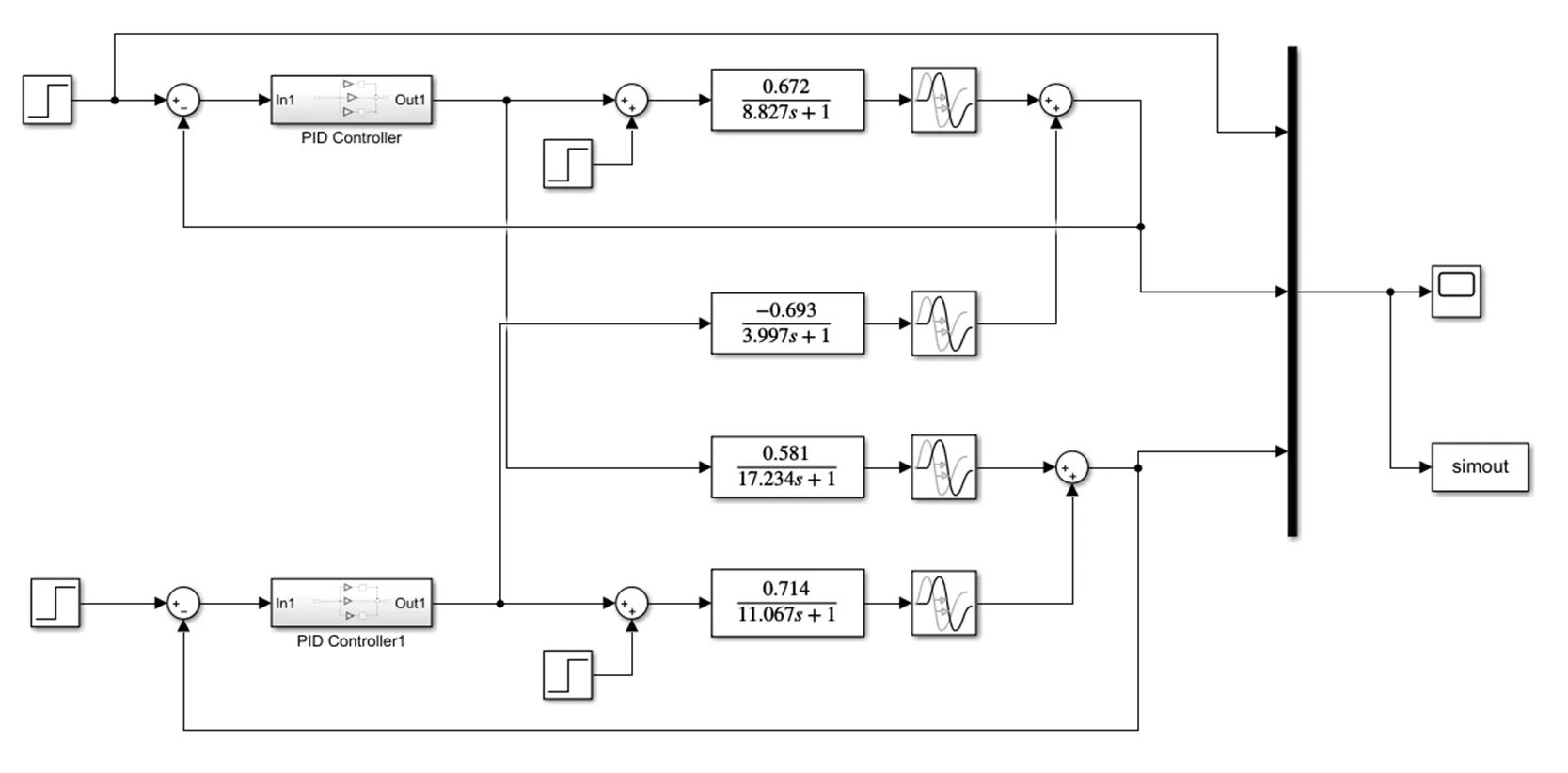
图3 挤出机的温度压力双变量耦合系统模型
多个单控制量的PID神经元网络可以构成多控制量的PID神经元网络。
2 PID神经元网络简介
PID神经元从结构上分为输入层、隐含层和输出层[7]。n个控制量的PID神经网络中包含n个相同的并行子网络,每个子网络相互独立,通过网络权值相互连接。每个子网络的输入层有两个神经元,一个神经元接收控制量的目标值,另一个神经元接收控制量的当前值。该子网络的隐含层由三个神经元组成,分别为比例元、积分元和微分元,这三个神经元的控制规律与PID控制器的控制规律相对应。而本文研究为二输入二输出的系统,因此其神经元网络的拓扑结构如图4所示。
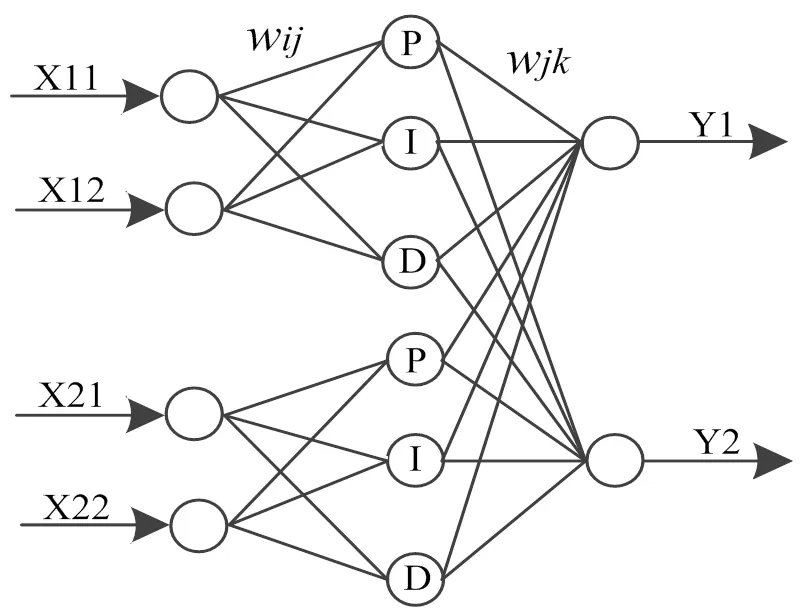
图4 双输入双输出PID神经元拓扑结构图
从PID神经元网络拓扑图所示,输入层有四个神经元,隐含层有两个比例神经元、两个积分神经元和两个微分神经元,共6个神经元。
输入层的神经元输出值等于输入数据,计算公式为:
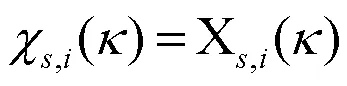
隐含层各神经元输入计算公式为:
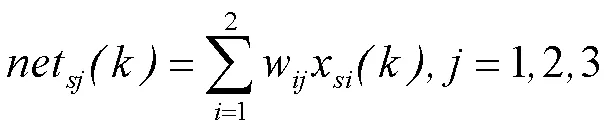
隐含层各比例、积分、微分神经元输出计算公式为:
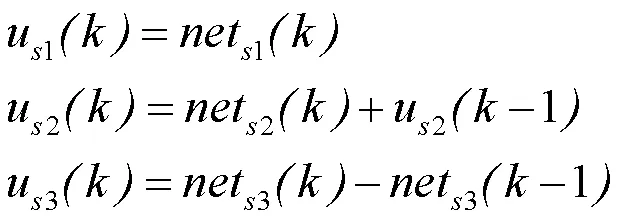
输出层有2个神经元,每个神经元的输出值为隐含层的全部输出值加权和,计算公式为:
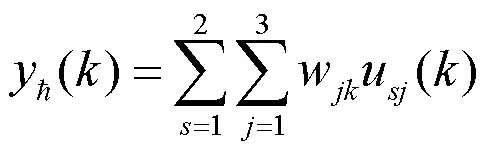
式中,为输出层神经元序号,为子网络序号,为隐含层神经元序号,sj()为子网络隐含层各神经元输出值,ik为隐含层至输出层的连接权重值。
在PID神经元网络控制过程中,其根据控制量的误差采用梯度下降法修正权值,计算公式为:
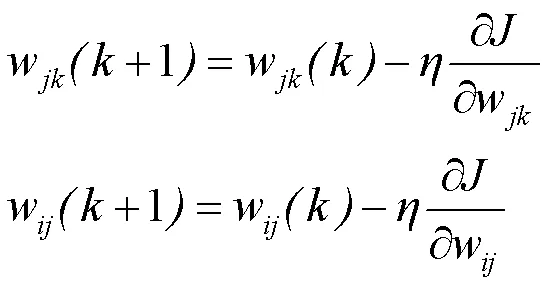
当前输出值与控制目标的差值,定义为误差函数:
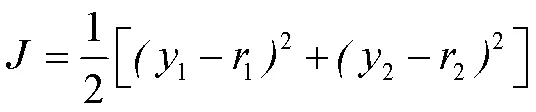
3 麻雀搜索算法的实现
受麻雀觅食行为和反捕食行为的启发,沈波[8]提出了麻雀搜索算法(Sparrow Search Algorithm,SSA),这种新型群智能优化算法模拟了麻雀群体的智慧、觅食和抗捕食的行为,并在模拟之后可以得出最优解。实验证明,该算法在收敛速度、稳定性和精度都具有较好的性能。
为了获取食物,麻雀个体以不同的身份进行觅食,它们可以被分为发现者和加入者。发现者在种群中负责寻找食物并为整个麻雀种群提供觅食区域和方向,而加入者则是利用发现者来获取食物[6]。同时发现者可以转换为加入者,而加入者也可以转变为发现者,这取决于麻雀群体在觅食时发现食物的先后。此外一方面由于处于外部的麻雀更易被捕获,因此它们会不断的调整自己的位置。另一方面,当麻雀种群受到威胁时会飞往其他地方觅食。沈波[8]使用理想化的麻雀种群,制定相应的规则。
(1)发现者行为个体通常有较高水平的能量储备,它负责识别并找到丰富的食物来源。能量储备的水平高低取决于个体适合度值的评估的好坏。其数学模型为:
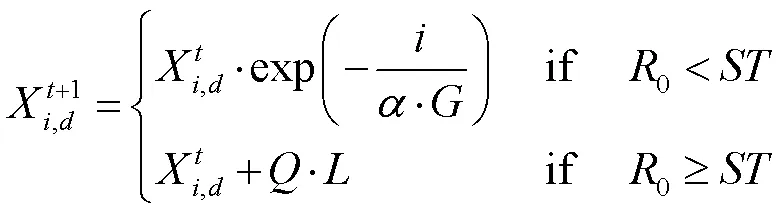
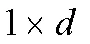
(2)一旦麻雀发现捕食者,它们就开始发出啁啾声,以提醒麻雀种群对周围进行警戒。如果报警值大于安全阈值,发现者则将种群的加入者引导至安全区域。
(3)发现者和加入者在整个种群中的比例通常是不变的,即当加入者在发现更好的觅食区域时,将会变为发现者,此时就会上一个觅食区域的发现者就转变为加入者。
(4)通常能量较低的加入者处在较差的觅食位置。这会导致一些能量获取不足的加入者飞往其他地方寻找食物,以找到更好觅食位置获得更多的能量。
(5)大部分加入者跟随可以找到最好觅食区域的发现者。为了增加自己的获取最佳食物的概率,其中一部分加入者也会不断监视发现者,与之争夺食物。加入者的数学模型为:
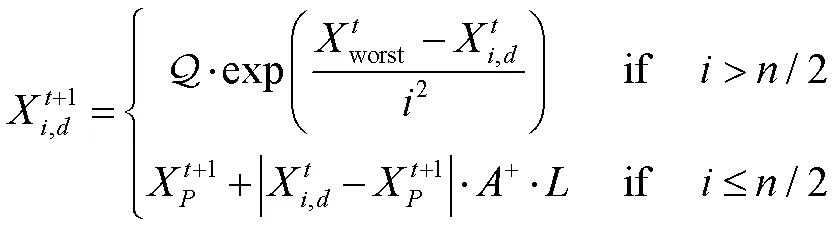
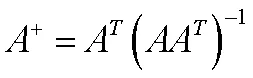
(6)麻雀受到外部威胁时,随即做出警戒行为,向着最佳食物源的麻雀个体移动,以获取更好的位置,而处于最佳觅食位置的麻雀则会执行随机走动操作,以接近其他麻雀。若麻雀种群中10%~20%的个体意识到危险,则这些麻雀个体的初始位置在麻雀群体中随机产生,其数学模型为:
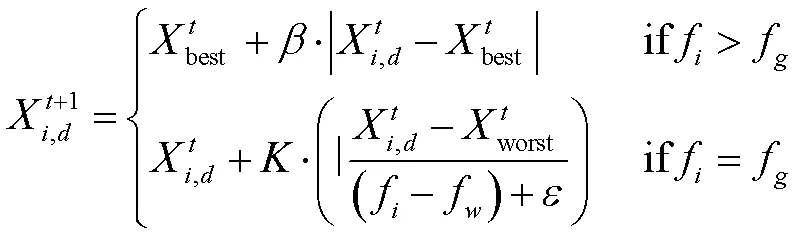
式中,tbest为种群当前全局最优觅食位置,是从标准正态分布中选取的一个随机数,同时作为步长控制参数,i代表当前麻雀个体的适应度,a则是当前全局最优适应度,w为当前全局最差适应度,为一个极小值。
4 基于SSA优化的PID神经元网络解耦控制
PID神经元网络的初始权值对网络的解耦性能有着重大影响,通常情况PID神经元网络的初始权值为随机数,然后在系统运行过程中对权值进行修正,直至误差达到要求。在该过程中权值可能需要多次修正,如图5所示,使用麻雀搜索算法对初始权值进行优化,给定较好的初始权值,可以减少权值的修正次数,以提高系统的运行效率。
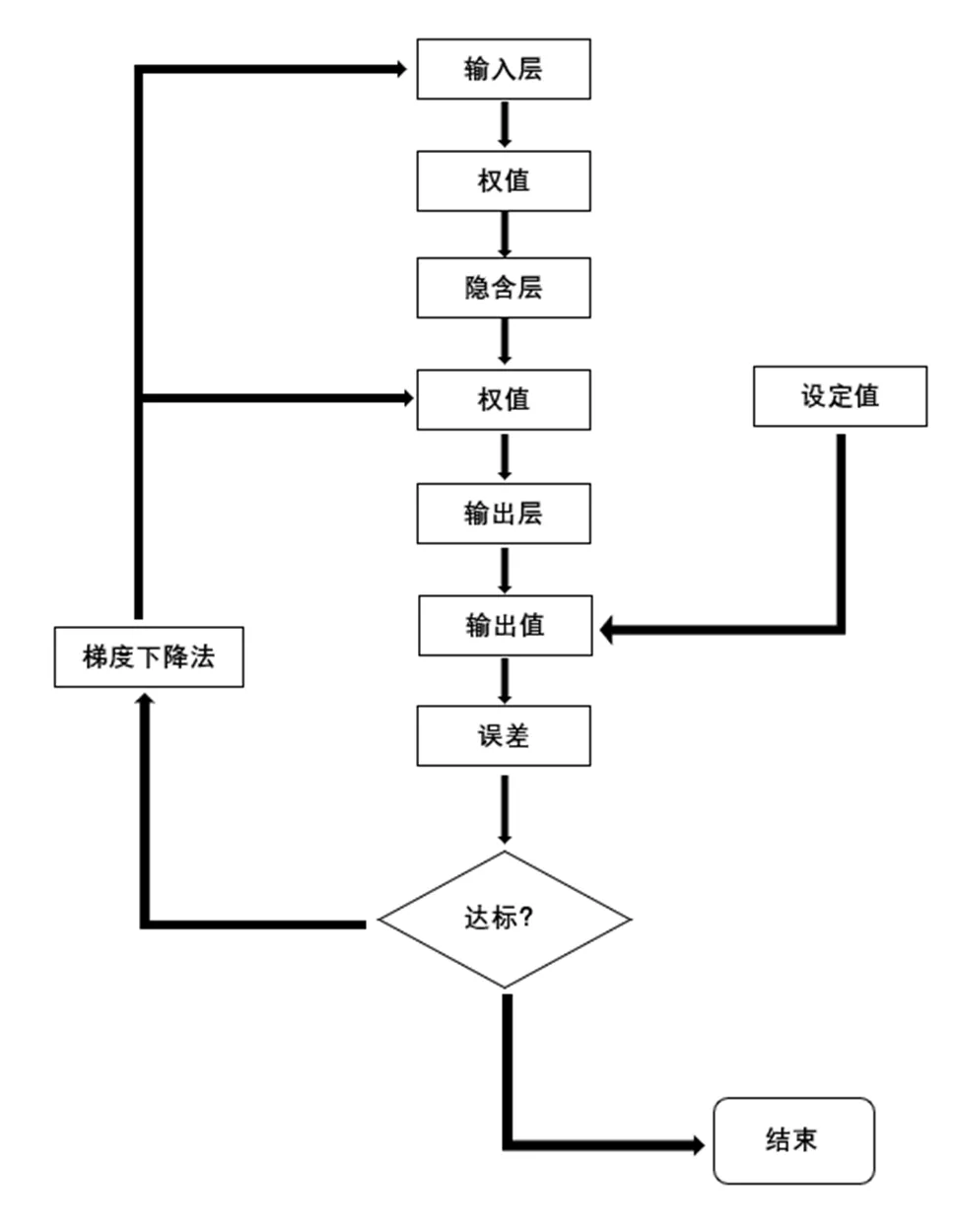
图5 PID神经元网络权值修正流程
采用麻雀搜索算法优化PID神经元网络初始权值,麻雀搜索算法种群数量设置为50,发现者比例设置70%,加入者为30%,预警值ST为0.6,迭代次数为40次。
优化后其中x11到隐含层的权值分别为0.0611、0.0542、0.0397;x12到隐含层的权值分别为0.0400、0.0507、0.0681;x21到隐含层的权值为0.0480、0.0398、0.0456;x22到隐含层的权值分别为0.0610、0.0593、0.0514;分别将神经元PID1的隐含层到输出层权值11’、21’、31’、41’、51’、61’设置为0.0537、0.0477、0.0527、0.0465、0.0684、0.0652;神经元PID2的隐含层到输出层权值12’、22’、32’、52’、52’、62’设置为0.0471、0.0452、0.0335、0.0469、0.0193、0.0600。
5 系统仿真
神经元PID网络拓扑结构如图1所示,采用经验法对系统权值进行初始化,其中x11到隐含层的权值分别为0.0436、0.0377、0.0379;x12到隐含层的权值分别为0.0285、0.0265、0.0121;x21到隐含层的权值为0.0331、0.0289、0.0095;x22到隐含层的权值分别为0.0073、0.0184、0.0285;分别将神经元PID1的隐含层到输出层权值11’、21’、31’、41’、51’、61’设置为0.0233、0.0748、0.0288、0.0175、0.0369、0.0045;神经元PID2的隐含层到输出层权值12’、22’、32’、52’、52’、62’设置为0.0267、0.0554、0.0279、0.0116、0.0386、0.0075。控制目标为[0.7 0.4],仿真结果如图6所示。
控制目标不变,使用优化后的初始权值,仿真结果如图7所示。优化前与优化后的误差变化如图8所示。

图6 挤出机耦合系统PID神经元网络控制仿真图
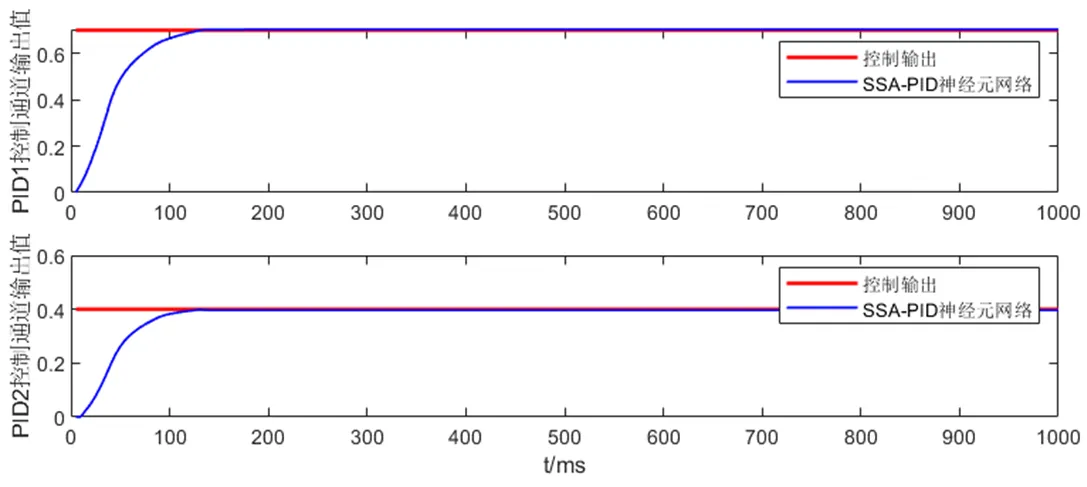
图7 挤出机耦合系统PID神经元网络控制仿真图
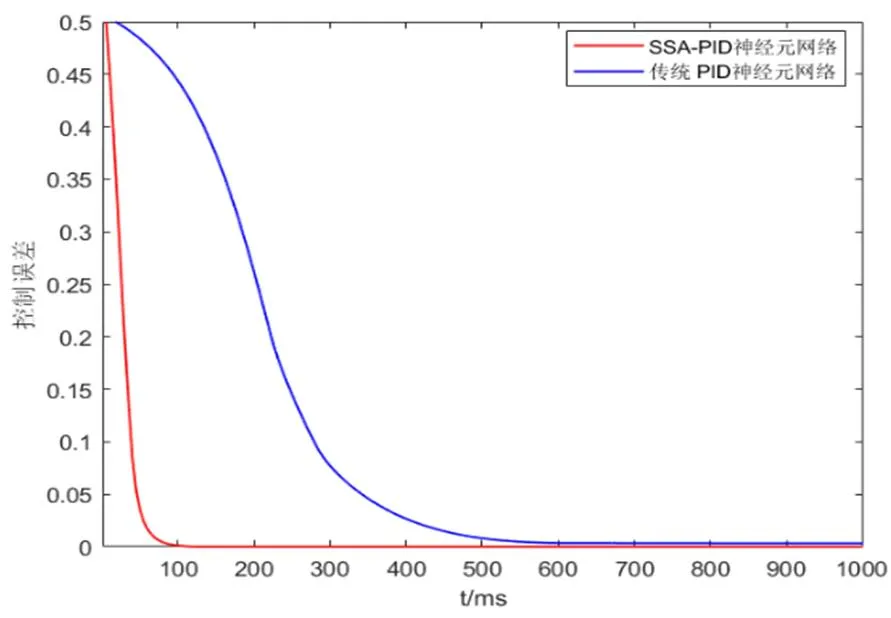
图8 目标函数误差曲线图
通过图6和图7可知,SSA-PID神经元网络响应速度更快,稳态误差更小。由图8可看出,PID神经元网络的误差下降曲线初始阶段下降速率较慢,SSA-PID神经元网络误差下降曲线下降阶段接近直线,下降总体速率处于PID神经元网络的误差下降最快阶段,说明SSA对PID神经元网络初始权值进行优化后,加快了解耦后的系统响应,使系统的动态性能和稳态性能更加优异。
6 结束语
通过SSA与PID神经元网络结合,提出了一种SSA-PID神经元网络的解耦控制系统,并在MATLAB软件进行仿真验证了解耦控制的性能及有效性。经分析发现,在使用SSA优化PID神经元网络的初始权值之后,解耦后的系统响应速度加快,动态性能更加优异,在上升时间和调节时间均更加优于PID神经元网络解耦控制。文中建立的SSA-PID神经元网络解耦控制算法还进一步减小了解耦之后的系统稳态误差,使得挤出机温度压力控制系统进一步符合工艺生产要求。基于麻雀搜索算法优化的PID神经元网络解耦控制,能够自适应调整,并且有较好的解耦性能,可以在一定程度上提高挤出机的智能水平。
[1] 李向荣,李国帅. 基于模糊PID的橡胶挤出机温控系统研究[D]. 青岛: 青岛科技大学,2014.
[2] 陈明霞,张寒. 橡胶复合挤出机温度压力建模分析及其控制系统优化研究[D]. 桂林: 桂林理工大学,2019.
[3] 谢德伦. 橡胶挤出成型[M]. 北京: 化学工业出版社,2005.
[4] 张馨,游长江. 橡胶压延与挤出[M]. 北京: 化学工业出版社,2013.
[5] 安阳. 影响挤出工艺的因素[J]. 现代橡胶技术,2006(1): 32-35.
[6] 舒怀林. PID神经元网络多变量控制系统分析[J]. 自动化学报,1999,25(1): 105-111.
[7] 李敦桥. 一种混沌麻雀搜索算法[J]. 计算机工程应用技术,2021,17(5): 232-234.
[8] 沈波,薛建凯. 一种新型的群智能优化技术的研究与应用: 麻雀搜索算法[D]. 上海: 东华大学,2019.
Temperature and Pressure Decoupling Control of Rubber Composite Extruder based on Sparrow Search Algorithm
Rubber extruder is a key equipment for rubber products production. Its extrusion process is a multivariable large time-delay system, in which the two key process parameters of temperature and pressure are strongly coupled. Single variable control and traditional decoupling methods can not guarantee the quality of extruded products. In this paper, the two most important factors, temperature and pressure, are selected from the many factors that affect the production process of rubber compound extruder. Aiming at the coupling phenomenon of temperature and pressure in rubber compound extruder, sparrow search algorithm (SSA) is used to optimize and adjust the initial weight of PID neural network, so as to speed up the response speed and improve the stability of the system after decoupling. Using MTATLAB software, PID neural network and SSA-PID neural network are used to decouple the extruder temperature and pressure, and the results are compared. The results show that the SSA PID neural network decoupling control system has faster response speed and smaller steady-state error, and the dynamic performance and steady-state performance of the system have been improved.
rubber compound extruder; sparrow search algorithm; PID neural network; decoupling control system
TQ33
A
1008-1151(2022)07-0009-05
2022-04-11
大学生创新创业训练计划(202110596057)。
王冰(1999-),男,广西合浦人,桂林理工大学机械与控制工程学院学生,研究方向为工业自动化。
