四氧化三铁颗粒大尺度空中动态吸波
2022-08-05周海洋倪长安李金轩李木养洪诗泽赵华宋鑫华
周海洋, 倪长安, 李金轩, 李木养, 洪诗泽, 赵华,宋鑫华
(南昌大学建筑工程学院, 南昌 330031)
随着现代信息探测技术的快速发展和战场环境的瞬息万变,新型隐身探测技术对现代武器装备产生重大影响,成为现代战场新型电子化战争探测目标和捕获信息的重要手段[1]。目前,隐身探测手段包括雷达、红外、磁隐身、声隐身、可见光隐身等。现代雷达隐身技术,主要通过结构外形的改进减少雷达散射截面积或者通过表面涂敷吸波材料吸收、衰减和转化雷达波,从而达到隐身的目的[2]。自第二次世界大战以来,吸波材料在雷达方面应用越来越广泛,美国和德国等西方国家从吸波体的设计、制作到测试以及性能的改进等多方面开展研究。除了在飞机外形方面进行隐身设计外,还通过喷涂高性能隐身涂料的方式使得飞机具有高隐身的特性[3]。现有的吸波材料主要是通过吸波剂提供吸波性能,基体材料提供粘结和承载作用,或者通过电特性和承载特性一体化作用来达到吸波隐身的效果。但是,雷达吸波涂层在紫外线、氧气、热、温度骤变、湿度等各种因素的综合作用容易而出现开裂、脱落和吸收剂变质等失效形式,从而导致隐身性能降低甚至失效[4]。结构吸波要采用多种结构型式进行综合设计才能达到最佳的吸波隐身的效果,从而导致设计、制作工艺复杂、成本高等一系列问题。而利用烟幕干扰技术不仅高效价廉,且能够在空间中制造大尺度隐身范围,有效的躲避侦查搜索、红外和激光制导等军事打击[5]。
羰基铁粉由五羰基铁化合物Fe(CO)5加热到70~80 ℃时开始分解成Fe和CO,在155 ℃时大量分解,形成葱头状结构的羰基铁粉[6];其在微波频段具有较高的磁导率、比饱和磁化强度,且温度稳定性好,被广泛应用在涂敷型雷达吸波上[7-9]。四氧化三铁(Fe3O4)是广泛应用的几种常见铁氧体材料中的一种,Fe3O4同时含有Fe2+和Fe3+,是一种反尖晶石结构。四氧化三铁颗粒从微米到纳米具有不同的尺寸,且都具有吸波特性。其中纳米尺寸的四氧化三铁吸波材料化学性质稳定,粒径可降至几纳米,具有高催化活性、良好磁响应性、耐候性、耐光性和生物相容性等特点,且对电磁波具有良好的吸收和屏蔽作用[10]。纳米四氧化三铁其独特的表面效应、量子尺寸效应、宏观量子隧道效应和小尺寸效应等性质,使得其在宽频段上具有优异的吸波性能[11]。因此,纳米四氧化三铁吸波材料的使用可以提高吸收剂的吸收性能,从而在军事隐身领域中被广泛使用。
目前,众多专家学者对四氧化三铁颗粒从制备到成分组成、微观结构等方面进行了研究,并用传输线法计算其在各个波段的吸波性能,即对其吸波的研究仅仅局限于毫米量级尺度的描述。为了进一步验证四氧化三铁颗粒在大尺度空间的吸波效果,Song等[12-13]通过球磨法将四氧化三铁纳米颗粒和碳纳米管进行复合,并计算模拟其在大尺度空间的静态吸波效果,初步的研究成果验证四氧化三铁/碳纳米管纳米复合材料应用在大尺度空间雷达波厘米波段的吸波效果是可行的。而实际过程中,颗粒通过云爆散布在大尺度空间中是随着时间在动态变化的一个过程,现研究微米和纳米两种不同尺寸四氧化三铁颗粒在大尺度空中真实的动态吸波特性,更真实地还原爆轰抛散的吸波衰减过程,并对其吸波机理进一步分析。
1 Fe3O4颗粒喷射分散数值模拟分析
运用大型流体力学软件Ansys-Fluent,应用离散相模型(discret phase model,DPM)研究在云爆装置产生的高压作用下粒径长分别为0.25 μm和10.57 nm的Fe3O4颗粒在大尺度空中喷射分散的运动过程,并分析空间内不同区域Fe3O4颗粒浓度与时间变化的动态关系。
1.1 数值模型定义
针对云爆装置爆炸产生巨大压力从而喷射Fe3O4颗粒的现象,建立了大尺度空中Fe3O4颗粒喷射分散的数值计算模型。假设云爆装置在爆炸瞬间产生一个长轴0.25 m、短轴0.15 m的椭圆高压空间,压强为100 atm(1 atm=1.01×105Pa),高压空间存在时间为6 ms。将Fe3O4颗粒喷射散布空间简化为半径为3 m的球形大尺度空间,取过球心的纵向截面为研究对象。同时采用结构化网格进行网格划分,自适应法完善网格,根据流场压力梯度的分布,在梯度较大处加密,较小处粗化,网格总数为23 452个[14],如图1所示。
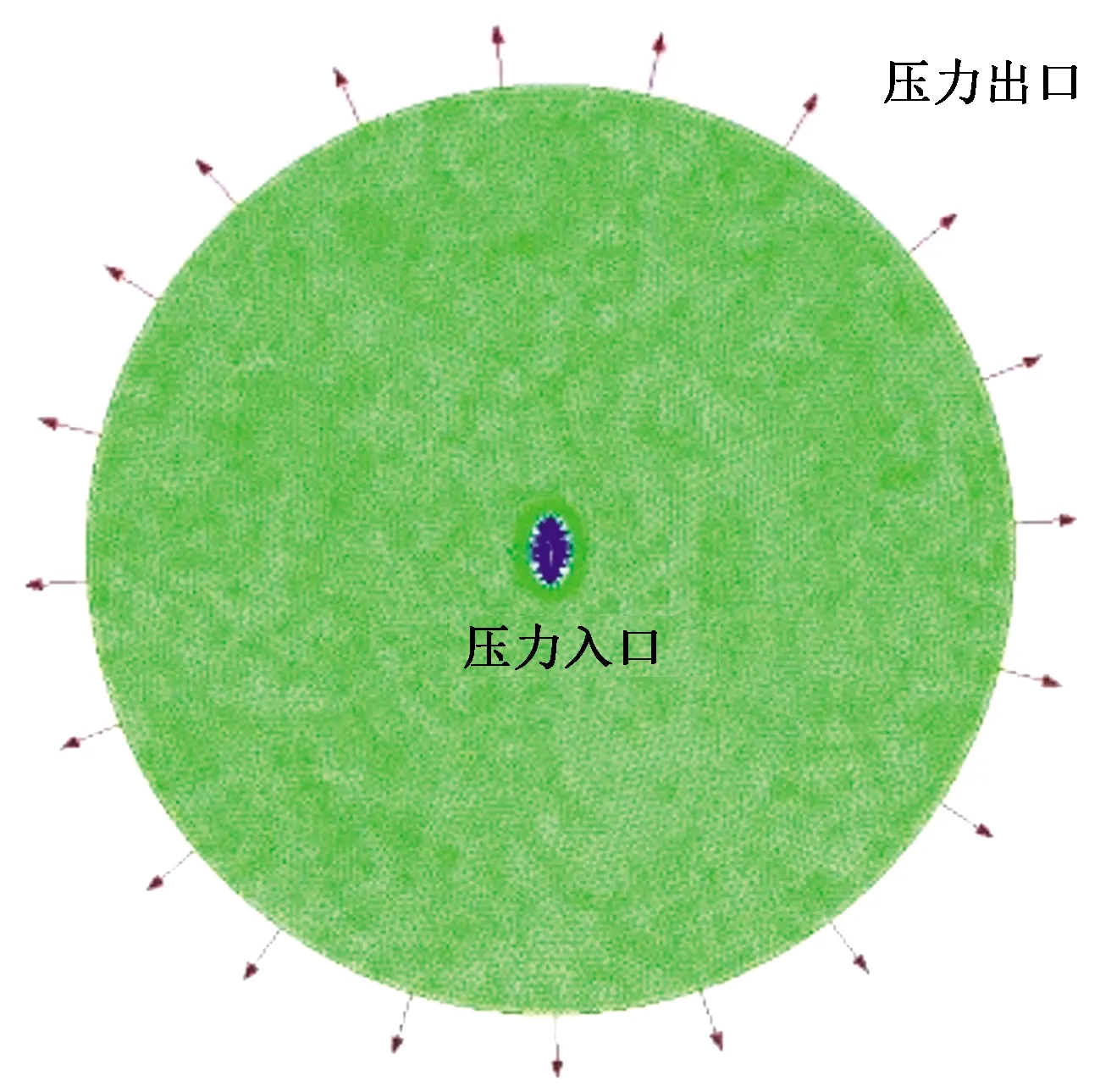
图1 数值计算网格划分图Fig.1 Numerical calculation meshing diagram
1.2 初始设置
采用基于压力求解器,DPM模型进行模拟,将Fe3O4颗粒做离散相计算,颗粒注入时间为6 ms,注入颗粒直径分别为0.25 μm和10.57 nm。工作环境中设置重力加速度9.81 m/s2,Y轴负方向。压力入口命名为pressure-inlet,初始表压力设置为100 atm,压力出口命名为pressure-outlet,表压力设置为0。压力出入口的湍流强度和湍流耗散能分别为5%和10%。在求解时选择压力耦合方程组的半隐式算法,连续性方程残差收敛极限均设为10-3,使用all-zone进行全局初始化,迭代时间步长5×10-5s,迭代时间步数为300步,每个时间步长迭代25次[15],模拟Fe3O4颗粒在15 ms内的喷射分散过程。
1.3 不同粒径Fe3O4颗粒散布浓度分析
选用粒径大小分别为0.25 μm和10.57 nm的Fe3O4颗粒进行数值模拟分析,选取距离高压空间的中心点水平距离1 m处的点和垂直上方这个点1 m的点为监测点,由于监测位置为一个点,其得到的浓度与时间变化曲线误差比较大,故选取各监测点为圆心,半径为0.1 m的圆形区域进行加权平均作为该监测点的浓度变化曲线[16]。如图2所示为粒径长为0.25 μm和10.57 nm的Fe3O4颗粒监测点浓度和时间变化曲线图。
由图2可知,距离高压空间的中心1 m处,粒径大小为0.25 μm的Fe3O4颗粒在0.55 ms时到达此处,在0.65 ms时该处浓度到达最大峰值,此时浓度达到0.115 kg/m3;粒径大小为10.57 nm的Fe3O4颗粒在0.52 ms时到达此处,在0.63 ms时该处浓度到达最大峰值, 此时浓度达到0.112 kg/m3。在Fe3O4颗粒喷射分散过程中,监测点(1,0)处浓度达到最大峰值后会快速下降,维持在一个低浓度值处上下波动,此时浓度分别为0.014 kg/m3和 0.012 kg/m3。

图2 Fe3O4颗粒监测点浓度与时间变化曲线图Fig.2 Curve of Fe3O4 particle concentration and time change at monitoring point
2 等效电磁参数推导与计算
第1节通过数值模拟得到粒径长分别为0.25 μm和10.57 nm的Fe3O4颗粒在大尺度空间内喷射分散过程中浓度随时间变化的曲线图,本节使用网络矢量分析仪测量出2~18 GHz频率范围内粒径长分别为0.25 μm和10.57 nm的Fe3O4颗粒相对电磁参数,并根据强扰动法对Fe3O4颗粒散布大尺度空间的电磁参数进行等效计算,最后推导计算出2~18 GHz频率范围内等效电磁参数式和18 GHz频率下浓度随时间变化的动态等效电磁参数。
2.1 相对电磁参数测量
取球磨混合后质量分数分别为50%的Fe3O4粉末和固体石蜡进行均匀的混合, 然后用模具制成外径为7.00 mm、内径为3.04 mm、厚度为2 mm的圆环,如图3(b)所示, 网络矢量分析仪如图3(a)所示。采用同轴线法,用网络矢量分析仪HP-8722ES进行测量,测得其在2~18 GHz频率范围内的电磁参数[17],如图4所示。

图3 电磁参数测试仪器Fig.3 Electromagnetic parameter test instrument

ε′表示等效介电参数的实部,μ′表示磁导率的实部; ε″表示介电参数的虚部,μ″表示磁导率的虚部图4 Fe3O4颗粒相对电磁参数Fig.4 Relative electromagnetic parameters of Fe3O4 particles
2.2 等效电磁参数推导[18]
根据强扰动理论对Fe3O4颗粒分散在空气媒质中进行等效计算,假设Fe3O4颗粒的介电参数为εs,空气的介电参数为εe,将Fe3O4颗粒和空气两相混合,设Fe3O4颗粒所占的体积比为fs,空气的体积比为fe,故有
fs+fe=1
(1)
由扰动项相关系数系宗平均值为0,即

(2)
求解得等效介电参数公式为
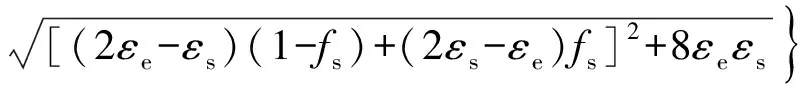
(3)
令Fe3O4颗粒的质量记为m(kg),浓度记为w(kg/m3);颗粒密度记为ρ(kg/m3);Fe3O4颗粒体积记为V1(m3),总体积记为V(m3),体积比记为fs,有
wV=m=ρV1
(4)
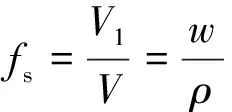
(5)
将式(5)代入式(3)得等效介电参数为
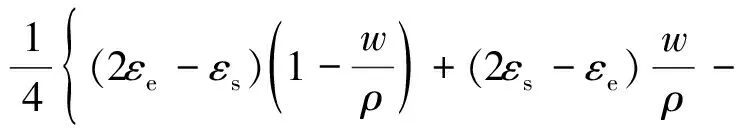

(6)
2.3 2~18 GHz频率范围内等效电磁参数计算
已知空气的介电常数为εe=1,εeff-t关系式、扩散过程中粒径长分别为0.25 μm和10.57 nm的Fe3O4颗粒浓度保持稳定时数值和2~18 GHz频率范围下Fe3O4颗粒的相对电磁参数,将上述数值代入式(6)可求得Fe3O4颗粒等效电磁参数数值,如图5所示。
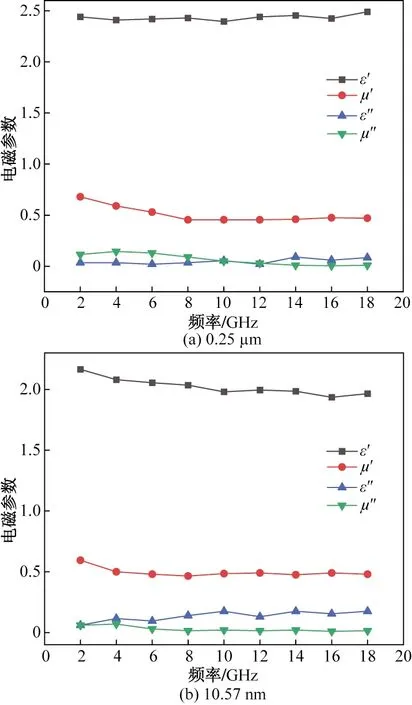
图5 Fe3O4颗粒的等效电磁参数Fig.5 Equivalent electromagnetic parameters of Fe3O4 particles
2.4 18 GHz频率下动态等效电磁参数计算
已知空气的介电常数是εe=1,εeff-t关系式、粒径大小分别为0.25 μm和10.57 nm的Fe3O4颗粒喷射分散时浓度随时间变化的函数关系式和18 GHz频率时Fe3O4颗粒的相对电磁参数,将上述数值带入式(6)可求得Fe3O4颗粒动态等效电磁参数,如图6所示。
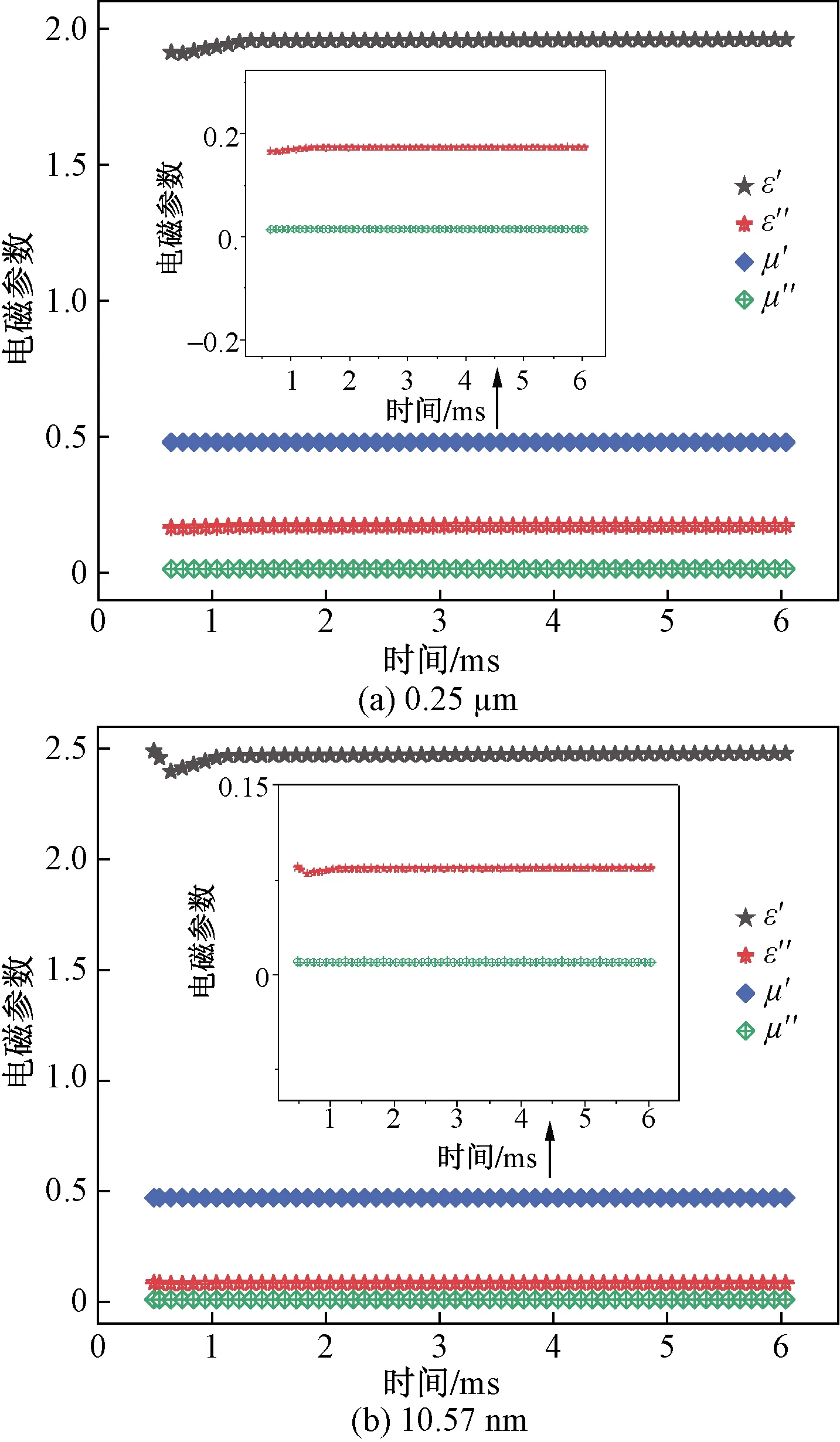
图6 18 GHz频率下Fe3O4颗粒的动态等效电磁参数Fig.6 Equivalent electromagnetic parameters of Fe3O4 particles at 18 GHz frequency
3 Fe3O4颗粒动态吸波效果研究
第2节推导了Fe3O4颗粒强扰动法下的等效电磁参数公式并计算得到了粒径长分别为0.25 μm和10.57 nm的Fe3O4颗粒在2~18 GHz频率范围内等效电磁参数和18 GHz频率下动态等效电磁参数。本节运用COMSOL Multiphysics软件中的RF模块模拟计算Fe3O4颗粒在入射电磁波频率为2~18 GHz范围下的电磁损耗和18 GHz频率时随时间变化的动态电磁损耗来研究大尺度空中Fe3O4颗粒吸波效果。
3.1 数值模型定义
假设云爆装置在空中爆炸,Fe3O4颗粒在球形空间分散且均匀分布。当地面雷达发出电磁波侦察时,发射器远离云爆空间,入射电磁波视为平面波。Fe3O4颗粒吸波效果数值模拟仿真结构示意图如图7(a)所示。外圆c3是完美匹配层[19],可以将模型范围限制在有限区域内,最大限度地减少模型域的非物理反射。内圆c2为空气层,内圆c1为Fe3O4颗粒的分布空间,根据PML网格生成的需要,使用扫掠网格划分,外圆半径长度应大于5~6个网格单元,内圆半径应根据云爆空间大小进行选择。为减少计算量,选取1/4云爆高压空间为计算模型,对Fe3O4颗粒空间域使用自由四面体网格划分,图7(b)、图7(c)分别为数值模拟仿真计算模型图和网格划分图。

图7 数值模拟仿真示意图Fig.7 Schematic diagram of numerical simulation
3.2 域与边界方程
在Comsol Multiphysics的射频模块中,雷达的背景电磁场用其平面外电场分量描述为
Eb=exp[ik0(xcosθ+ysinθ)]ez
(7)
式(7)中:i为虚数单位;k0=2πf/c为真空中波束,c=3×108m/s为光速;f为频率;θ为入射角,θ=0对应入射波为x正方向。 模型沿x轴负方向从右向左传播。根据相对场的时间谐波方程得
Erel=E-Eb
(8)
式(8)中:E为总体可测场。电磁波空间平面方程可表示为

(9)
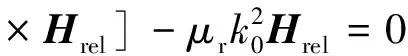
(10)
式中:μr是相对磁导率;εr为相对介电常数;i为虚数单位;σ为电导率;ω为角频率;ε0为真空的介电常数;k0为自由空间电磁波数量。均由Maxwell方程组推导出来的电磁波方程,可以用来射频模块的稳态分析、频域分析和模态分析[20]。
3.3 2~18 GHz频率范围内吸波损耗模拟分析
当2~18 GHz频率范围内电磁波入射到粒径长分别为2.5 μm和10.57 nm的Fe3O4颗粒散布空间中,代入此时Fe3O4颗粒的动态等效电磁参数,电磁损耗数值模拟结果如图8所示。

图8 Fe3O4颗粒电磁损耗数值模拟图Fig.8 Numerical simulation diagram of electromagnetic loss of Fe3O4 particles
从图8看出,随着入射电磁波频率的增大,总体趋势上Fe3O4颗粒分散空间产生电磁损耗越来越大。当入射电磁波频率在2~18 GHz范围内时,10.57 nm的Fe3O4纳米颗粒散布空间产生的电磁损耗较大,电磁损耗为0.40~11.59 W,电磁波吸收效果较好;0.25 μm的Fe3O4颗粒散布空间产生的电磁损耗较小, 电磁损耗为0.22~4.88 W,电磁波吸收效果较差。当入射电磁波频率为18 GHz时,10.57 nm的Fe3O4纳米颗粒散布空间产生的电磁损耗达到了11.59 W,粒径长为0.25 μm的Fe3O4颗粒散布空间产生的电磁损耗达到了4.88 W。
3.4 18 GHz频率下动态吸波损耗模拟分析
当18 GHz频率的电磁波入射到粒径长分别为0.25 μm和10.57 nm的Fe3O4颗粒散布空间中,代入此时Fe3O4颗粒的等效电磁参数,动态电磁损耗数值模拟结果如图9所示。

图9 18 GHz频率下Fe3O4颗粒电磁损耗数值模拟图Fig.9 Numerical simulation diagram of electromagnetic loss of Fe3O4 particles at 18 GHz frequency
从图9可以看出,随着入射电磁波频率的增大,总体趋势上Fe3O4颗粒分散空间产生电磁损耗呈上升趋势。在入射电磁波频率为18 GHz时,10.57 nm的Fe3O4纳米颗粒散布空间产生的电磁损耗较大,电磁损耗为11.381~11.559 W,电磁波吸收效果较好;0.25 μm的Fe3O4颗粒散布空间产生的电磁损耗较小,电磁损耗为4.812~4.899 W,电磁波吸收效果较差。
3.5 四氧化三铁颗粒吸波机理
在微波频段,羰基铁的磁损耗机制主要是自然共振和磁泄损耗,介电损耗则由电偶极子取向极化引起。由上文计算可知,纳米尺寸的Fe3O4的吸波损耗性能优于微米尺寸的Fe3O4,其原因主要是当羰基铁尺寸达到纳米级别的时候,其主要吸波机理主要有三方面原因:①纳米材料界面组元所占比例大,纳米颗粒的比表面积高,不饱和键和悬挂键多,大量悬挂键的存在使界面极化;②由于其纳米量子尺寸效应使得电子能级分裂,分裂得能级间距处于微波能量范围(10-2~10-4eV),为纳米材料创造了新的吸收通道;③纳米材料中原子和电子在微波场的辐照下,运动加剧,使得其电磁能转化为热能[21]。如图10所示。
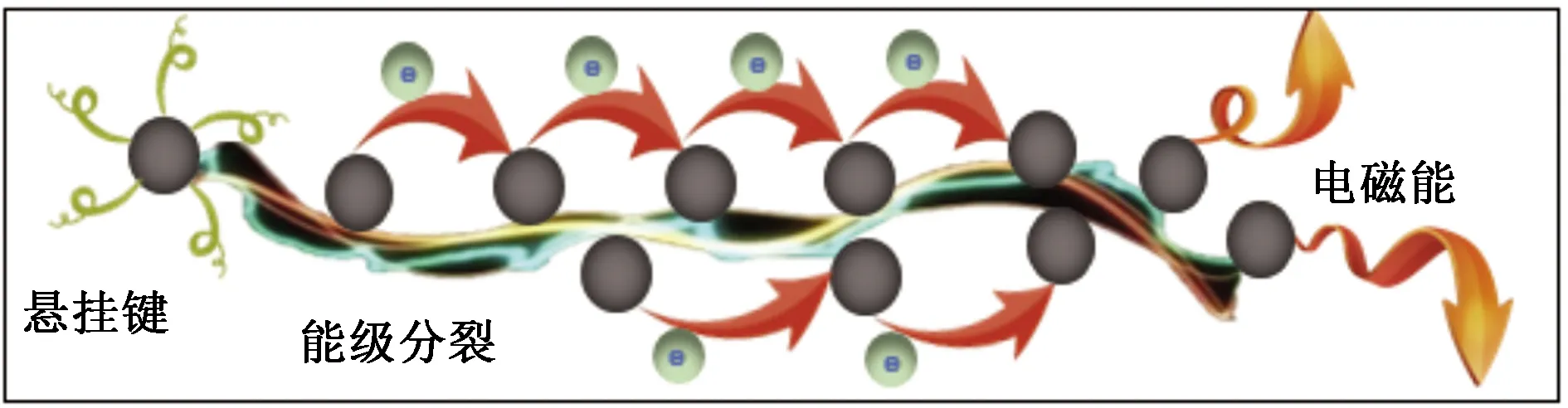
图10 纳米尺度Fe3O4的悬挂键极化损耗、 能级分裂损耗和电磁能转化成热能损耗Fig.10 The polarization loss of suspension bond, energy level splitting loss and the loss of electromagnetic energy conversion to heat energy of nanoscale Fe3O4
4 结论
采用Ansys-Fluent和Comsol Multiphysic软件,对粒径长分别为0.25 μm和10.57 nm的Fe3O4颗粒散布大尺度空间的动态电磁损耗进行数值模拟研究,尽管建立的数值模型忽略了一些影响因素,但是采用了一种全新的方法,较为成功地模拟了大尺度空中Fe3O4颗粒动态吸波效果。
首先,基于大型流体力学软件Ansys-Fluent,应用DPM模型进行模拟,研究在云爆装置产生的高压作用下粒径长分别为0.25 μm和10.57 nm的Fe3O4颗粒在3 m大尺度球形空间的喷射分散过程,并分析了空间内不同区域Fe3O4颗粒浓度随时间变化的关系。
其次,用网络矢量分析仪测量出2~18 GHz频率范围内粒径长分别为0.25 μm和10.57 nm的Fe3O4颗粒相对电磁参数,并根据强扰动法对Fe3O4颗粒散布大尺度空间的电磁参数进行等效计算,将Fe3O4颗粒在大尺度空间中浓度与时间拟合函数关系式代入等效电磁参数中,推导计算出2~18 GHz频率范围内等效电磁参数式和18 GHz频率时随时间变化的动态等效电磁参数。
最后,利用Comsol Multiphysics中RF模块,模拟计算粒径长分别为0.25 μm和10.57 nm的Fe3O4颗粒散布空间在入射电磁波频率为2~18 GHz范围内的电磁损耗和18 GHz频率时随时间变化的动态电磁损耗。研究结果表明,随着入射电磁波的频率的增大,总体趋势上Fe3O4颗粒散布空间产生的电磁损耗也逐渐增大。当入射电磁波频率为2~18 GHz范围内时,10.57 nm的Fe3O4颗粒散布空间产生的电磁损耗为0.40~11.59 W,入射电磁波频率为18 GHz时,产生的电磁损耗为11.381~11.559 W,电磁波吸收效果较好;当入射电磁波频率为2~18 GHz范围内时,0.25 μm的Fe3O4颗粒散布空间产生的磁损耗为0.22~4.88 W,入射电磁波频率为18 GHz时,产生的电磁损耗为4.812~4.899 W,电磁波吸收效果较差。最后从三个方面分析了纳米Fe3O4颗粒吸波性能优于微米Fe3O4颗粒的原因。
