基于极限学习机模型的空气质量二次预报
2022-08-05朱盛恺陈劲杰
朱盛恺,陈劲杰
(上海理工大学,上海 200093)
kaisss163@163.com;2502526194@qq.com
1 引言(Introduction)
大气污染系指由于人类活动或自然过程引起某些物质进入大气中,呈现足够的浓度,达到了足够的时间,并因此危害了人体的舒适、健康和福利或危害了生态环境。污染防治实践表明,建立空气质量预报模型,提前获知可能发生的大气污染过程并采取相应的控制措施,是减少大气污染对人体健康和环境等造成的危害,提高环境空气质量的有效方法之一。
但受制于模拟的气象场和排放清单的不确定性,以及对包括臭氧在内的污染物生成机理的不完全明晰,现有的WRF-CMAQ一次预报模型的预测结果并不理想。由于污染物浓度实测数据的变化情况对空气质量预报影响很大,故参考空气质量监测点获得的污染物实测数据对一次预报数据进行修正。通过对一次预报数据和实测数据的二次建模可以优化预测结果,能够提高对空气质量预测的准确率。
2 样本数据处理(Sample data processing)
数据来源为某监测点的样本数据库数据,数据包括污染物浓度一次预报数据和污染物浓度实测数据,其中主要为用于衡量空气质量的六种常规大气污染物,分别为二氧化硫(SO)、二氧化氮(NO)、粒径小于10 μm的颗粒物(PM)、粒径小于2.5 μm的颗粒物(PM)、臭氧(O)、一氧化碳(CO)。对初始数据进行处理(以SO的处理为例),在对数据的分析过程中发现气候与污染物浓度的数据表格中存在大量的缺失,此外,有许多异常值存在于测量数据中,图1中选取了部分数据示例。
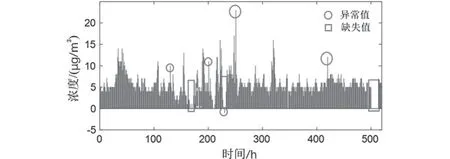
图1 SO2监测浓度部分数据Fig.1 Partial data of SO2 monitoring concentration
由于提供的数据并非完整天数的检测数据,根据每日预报的时间固定为早晨7 点,此时可以获得当日7 点及之前时刻的实测数据,按天对数据进行整理,剔除头部0 点到7 点的不完整数据,然后以整天为单位处理其余数据。
首先是对缺失值的处理,选择以小时为单位在MATLAB中调用interp1进行一维线性插值。插值后的数据如图2所示。
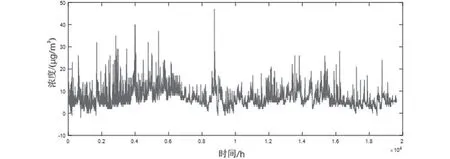
图2 SO2监测浓度缺失值插值结果Fig.2 Interpolation results of SO2 monitoring concentration with missing values
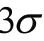
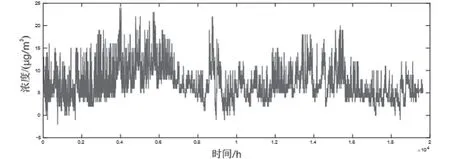
图3 SO2监测浓度去除异常值插值结果Fig.3 Interpolation results of SO2 monitoring concentration with removal outliers
根据《环境空气质量指数(AQI)技术规定(试行)》(HJ 633—2012),空气质量指数(AQI)可用于判别空气质量等级。空气质量等级范围根据AQI数值划分,等级对应的AQI范围如表1所示。
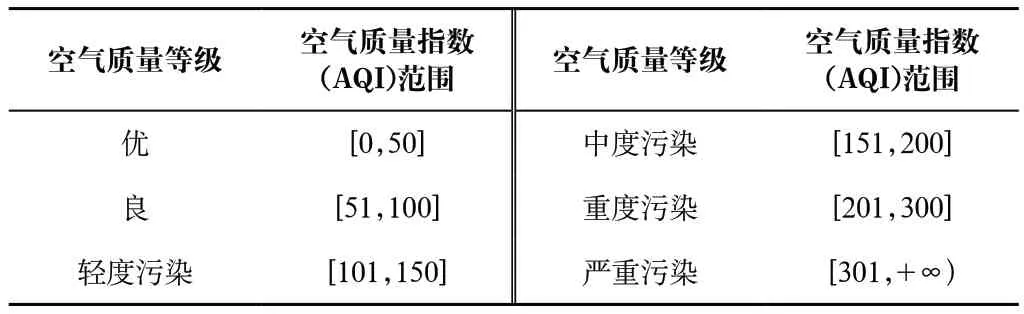
表1 空气质量等级及对应空气质量指数(AQI)范围Tab.1 Air quality level and corresponding air quality index (AQI) range
当AQI小于或等于50(即空气质量评价为“优”)时,称当天无首要污染物。当AQI大于50时,空气质量分指数(IAQI)计算值最大的称为首要污染物。若IAQI最大值相同时,并列为首要污染物。IAQI大于100的污染物称为超标污染物。
综合考虑以AQI和首要污染物的误差这两个指标的加权组合作为遗传算法的适应度。
首先得到各项污染物的IAQI,其计算公式如下:

AQI取各分指数中的最大值,即
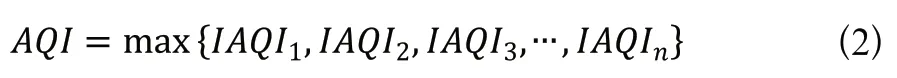
在本次研究中,对AQI的计算仅涉及六种污染物,因此计算公式如下:
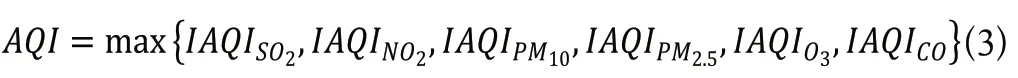
将数据库数据经过插值处理后再转换成AQI值,并记下对应的首要污染物,为后续分析做好准备。
3 极限学习机模型(Extreme learning machine model)
3.1 模型选择
传统的学习算法(如BP算法等)存在四方面的不足:训练时间长;所得到的网络性能差;因为某些特殊函数可能有局部极小点;网络学习率波动大,成为阻止其进化的主要障碍。而前馈神经网络往往采用梯度下降方法,也存在三个方面的不足:训练时间长;容易陷入局部极小点,无法达到全局最小;学习率的选择敏感。
极限学习机(ELM)模型网络结构算法不再是基于梯度的算法,而是随机产生输入层与隐藏层间的连接权值和隐藏层神经元的阈值,在训练中无须特殊操作,唯一值就是隐藏层神经元数量,训练完成后就可以得到全局最优解。与以往的训练方式比较,ELM模型具有训练速度快、泛用性广、误差非常小等优点,故选择ELM模型网络结构完成模型预测。
3.2 模型建立
ELM模型的网络结构与单隐藏层前馈神经网络(SLFN)一样,只不过在训练阶段不再是传统的神经网络中屡试不爽的基于梯度的算法(后向传播),而采用随机的输入层权值和偏差,输出层权重则通过广义逆矩阵理论计算得到。得到所有网络节点上的权值和偏差后,ELM的训练就完成了,这时通过测试数据,利用刚刚求得的输出层权重便可计算出网络输出,完成对数据的预测。
ELM训练基本上分为随机特征映射和线性参数求解。第一阶段,隐藏层参数随机进行初始化,然后采用一些非线性映射作为激活函数,将输入数据映射到一个新的特征空间(称为ELM特征空间)。简单来说,就是ELM隐藏层节点上的权值和偏差是随机产生的。随机特征映射阶段与许多现有的学习算法不同,ELM中的非线性映射函数可以是任何非线性分段连续函数。在ELM中,隐藏层节点参数(和)根据任意连续的概率分布随机生成(与训练数据无关),而不是经过训练确定的,从而使与传统BP神经网络相比在效率方面占很大优势。经过第一阶段、已随机产生而确定下来,可根据公式计算出隐藏层输出。在ELM学习的第二阶段,只需要求解输出层的权值()。为了得到在训练样本集上具有良好效果的,需要保证其训练误差最小,将(网络的输出)与(样本标签)进行计算,求得最小平方差作为评价训练误差,使得该目标函数最小的解就是最优解。即通过最小化近似平方差的方法对连接隐藏层和输出层的权重()进行求解,目标函数如下:
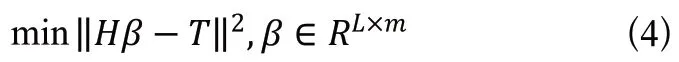
其中,是隐藏层的输出矩阵,是训练数据的目标矩阵。
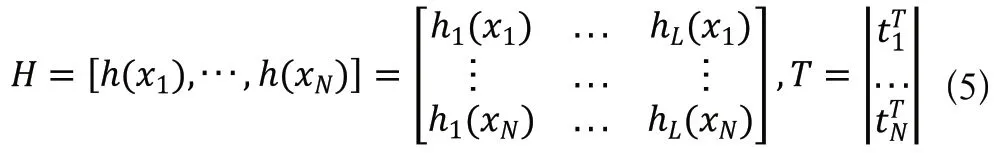
通过线代和矩阵论的知识可推导得到最优解为:

这时问题就转化为求计算矩阵的Moore Penrose广义逆矩阵。当HH(的转置与相乘)为非奇异(可逆)时可使用正交投影法,得到的计算结果是:

4 优化模型的建立(Optimization model building)
4.1 遗传算法优化的ELM模型
在模型建立上,发现ELM模型预测AQI的相对误差最大值最小,首要污染物误差最小,接着再选择用遗传算法优化现有预测模型,具体流程如图4所示。

图4 遗传算法优化的ELM模型建立流程图Fig.4 Flow chart of ELM model building for genetic algorithm optimization
确认好神经网络的输入输出对应关系,以AQI和首要污染物的误差这两个指标的加权组合作为适应度,随机设置一组要优化的惩罚因子和核参数。把数据分为80%训练集和20%测试集,以设置的参数和训练样本去训练模型,然后测试样本的输入与预测获得预测结果以计算预测的AQI值,并计算得出适应度函数,再按照流程图所示过程完成建模预测。
4.2 结果预测
预测将来某小时+1的一次预测结果时,采用滚动预测,结合该时间之前的真实时刻历史数据,可以获得该时间的二次预测结果。然后再预测+2 小时,+2之前+1这一时刻的历史数据就可以采用二次预测结果去预测,预测结果如图5—图10所示。通过真实值-预测值得到了对应点的预测误差数据,经过计算发现误差值均不超过10%。可以发现,该模型方法预测还是比较准确的。
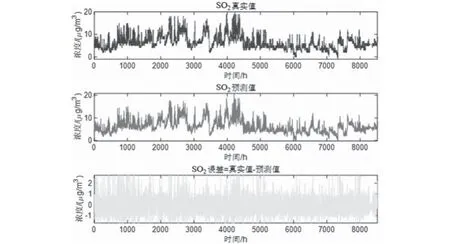
图5 SO2真实-预测-误差Fig.5 SO2 reality-prediction-error
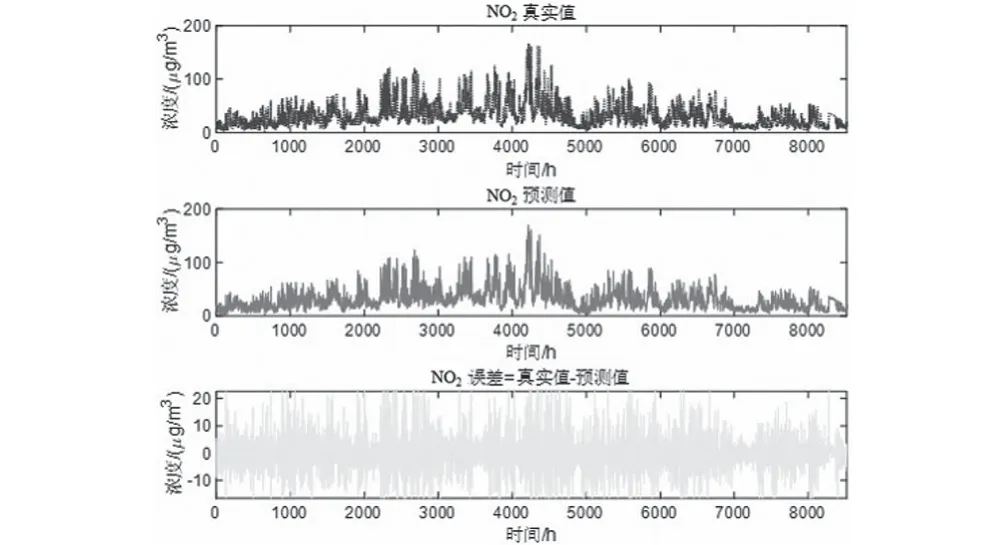
图6 NO2真实-预测-误差Fig.6 NO2 reality-prediction-error
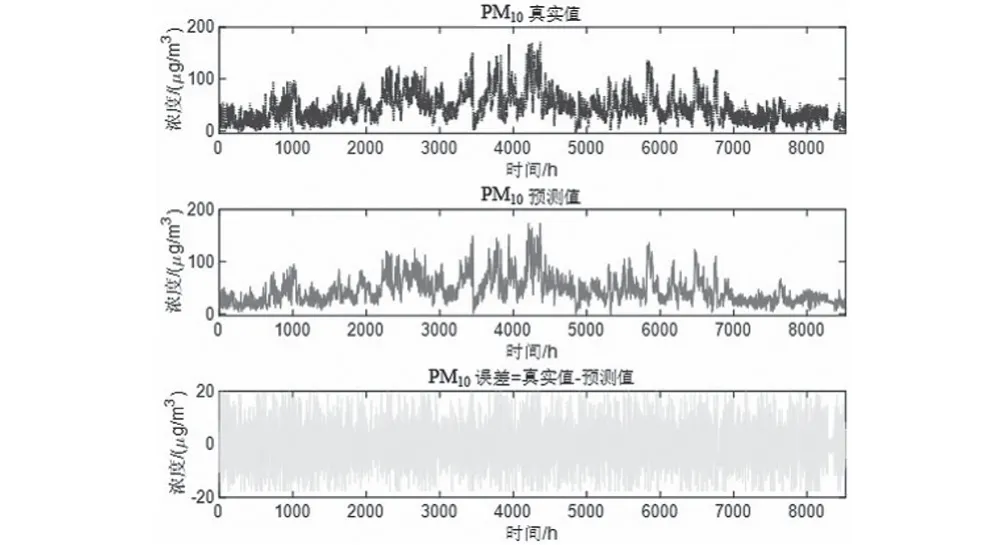
图7 PM10真实-预测-误差Fig.7 PM10 reality-prediction-error
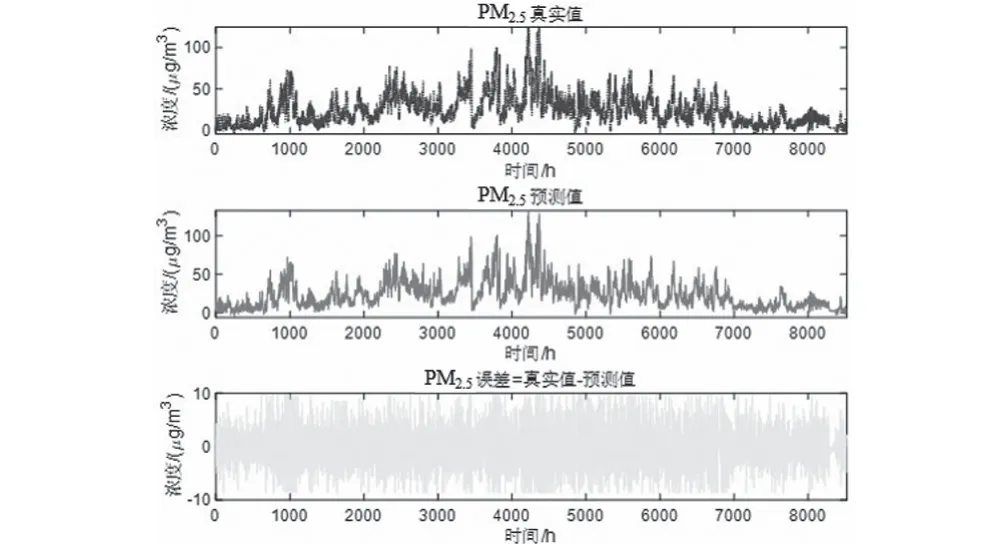
图8 PM2.5真实-预测-误差Fig.8 PM2.5 reality-prediction-error
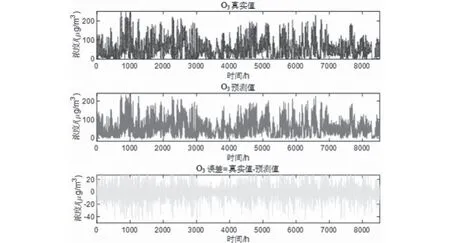
图9 O3真实-预测-误差Fig.9 O3 reality-prediction-error
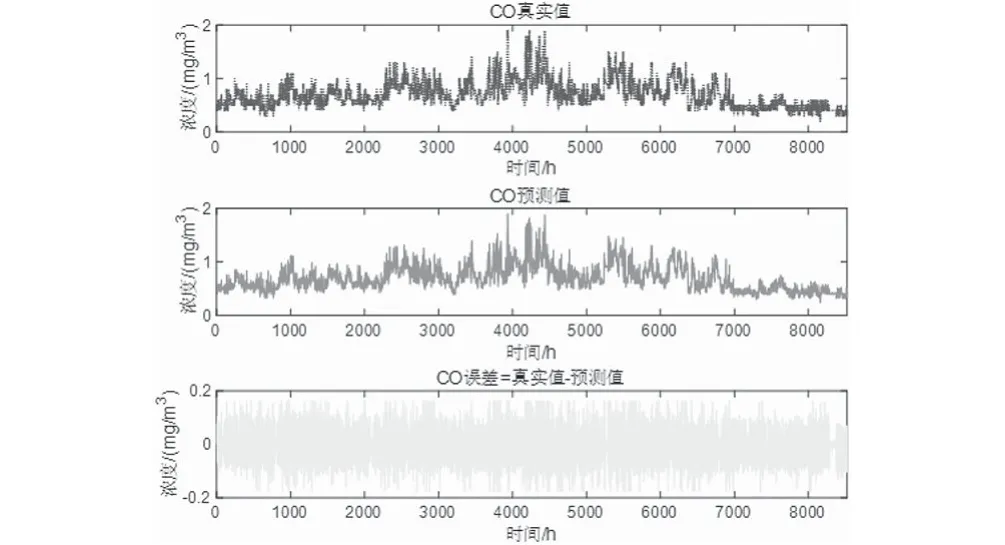
图10 CO真实-预测-误差Fig.10 CO reality-prediction-error
5 结论(Conclusion)
基于建立的ELM模型,结合遗传算法,得到优化后的六种污染物真实值与预测值最大误差均低于10%,而一次预报误差普遍在15%以上。利用该模型在WRF-CMAQ等一次预报模型模拟结果的基础上,结合监测点污染物实测数据进行再建模,提高了预报的准确性。
