应用声发射技术和图像分形理论对樟子松木材裂纹演化特征的检测1)
2022-08-04赖菲王明华肖洒丁锐罗蕊寒邓婷婷李明
赖菲 王明华 肖洒 丁锐 罗蕊寒 邓婷婷 李明
(西南林业大学,云南,650224)(安徽工程大学)
声发射(AE)技术,是根据材料在外加载荷作用下产生瞬态弹性波,判断材料内部损伤程度的动态无损检测技术[1]。目前在木材科学领域,声发射技术主要应用于木材缺陷检测[2]、载荷作用下的断裂行为研究[3]、木材损伤定位[4]等方面。关于木材断裂模式识别的相关研究中表明,高频高振幅的声发射信号是由于纤维断裂产生的,高频低幅值声发射信号源于木材水分蒸发,而低频低振幅的声发射信号则是由基体裂纹或界面裂纹引起的[5-6]。细胞壁断裂对应的声发射信号特征为高幅值、高能量,且持续时间长;而细胞壁界面损伤和压溃损伤对应的声发射信号特征为低幅度、低能量,且持续时间短[7]。纵观已有研究结果,多数集中于通过声发射事件、声发射能量等参数分析材料的损伤特性,在材料产生宏观断裂后,声发射参数只能定性判断木材损伤的程度;但有研究认为,研究材料表面宏观裂纹的演化特征,可以定量评估和实时监测断裂阶段的损伤过程[8]。
木材裂纹是非线性和不规则的几何形体,而图像分形理论研究的是自然界中存在的无序混乱和不规则形态的事物,可以描述其整体与局部或不同尺度下的自相似性,揭示复杂事物背后的规律。分形维数是所有分形对象的主要特征之一,是实现断裂表面定量分析的一种有效方法。已有研究表明,分形维数是研究各种物理现象的有力工具,可以反映岩石、混凝土、煤体、水泥、木材[9-12]的损伤演化程度。
为此,本研究将声发射技术与图像处理技术相结合,以气干状态的樟子松(Pinussylvestrisvar.mongolica)木材为试验材料,制备尺寸为(长×宽×厚)300 mm×20 mm×20 mm试验试件,应用UTM5105型电子万能力学试验机对试件进行三点弯曲加载试验;利用声发射采集平台和图像采集系统,实时采集樟子松木材在三点弯曲破坏过程中产生的声发射信号及裂纹演变图像;依据原始声发射波形统计声发射计数、声发射能量,并结合图像分析试件在加载过程中的微观损伤及其宏观演化特征;依据图像分形理论计算灰度图像及二值化图像盒计数维数,分析木材表面裂纹起裂和扩展规律;综合运用声发射技术和图像分形理论,构建樟子松木材裂纹演化特征的研究方法,既可以检测到材料在受载前期内部的微观损伤,又可以检测材料在产生宏观裂纹后其表面裂纹的演化特性;旨在为研究木材损伤断裂过程中裂纹演化行为的损伤机理提供参考。
1 材料与方法
1.1 试验材料
本研究选择3根尺寸相同的樟子松(Pinussylvestrisvar.mongolica)木材作为试验材料,分别编号为ZZS-1、ZZS-2、ZZS-3,试件尺寸均为(长×宽×厚)300 mm×20 mm×20 mm,试件的密度分别为0.420、0.410、0.418 g/cm3,气干状态下平均含水率在12.8%左右。试件表面人工喷涂油漆,即用白色哑光漆喷涂试件正面,便于CCD相机采集裂纹图像。
1.2 试验方法
试验装置由加载系统、声发射(AE)信号采集系统、图像采集系统构成(见图1)。采用UTM5105型电子万能力学试验机对试件进行三点弯曲加载试验,力学试验机压头正对试件中点,以垂直木材顺纹理方向加载,加载速度为5 mm/min,跨距设置为200 mm。

(a)为实物图;(b)为声发射信号采集系统。
利用NIUSB-6366高速采集卡和LabVIEW软件,搭建2通道声发射信号采集系统,同步采集声发射信号;其中,声发射信号采集系统由计算机、传感器、信号分离器、数据采集卡、信号传输器、前端放大器组成;传感器为SR 150 N单端谐振声发射传感器,前置放大器增益为40 dB、带宽22~220 kHz;根据香农采样定理,设置每个通道的采样频率为500 kHz,输出电压范围设置为(-5 V,5 V)。2个声发射传感器分别位于距试件中点50 mm的左右两侧,为了保证传感器与试件充分耦合,在试件与传感器之间涂上真空绝缘硅脂,以减少空气介质对试验结果的影响,并利用橡皮筋将传感器固定在试件表面。
利用UC30工业相机(CCD相机)采集试件正面受载的实时图像。相机的镜头长度为2.8~12.0 mm,分辨率为1920×1080@60FPS;CCD相机安装于三脚架上,放置于试件正前方70 mm处,采集频率设为1帧/s。同时启动万能力学试验机、CCD相机、声发射信号采集系统,实现试件三点弯曲试验过程的力值数据、图像、声发射信号同步采集;当载荷快速下降时停止加载,同时停止声发射采集系统和图像采集系统。
1.3 木材图像的盒计数维数计算方法
分形维数是对图像自相似性的一种度量,裂纹图像的分形维数在一定程度上反映了裂纹扩展的不确定性。尽管计算图像分形维数的方法有很多,盒计数方法作为意义明确且操作简单的一种分形维数计算方法,仍被广泛用于计算图像的分形维数,由此得到的分形维数也称为盒计数维数。
设A是Rn空间的任意非空子集,对于任意的1个r>0,Nr(A)表示用来覆盖A所需边长为r的n维立方体的最小数目。如果存在1个数d,使得当r→0时有Nr(A)∝1/rd,称d为A的盒计数维数。当且仅当存在1个正数k,使得limr[Nr(A)/(1/rd)]=k(式中r→0)。由于上述方程的两边都为正数,因此可以对方程两边取对数,得limr[logNr(A)+dlogr]=logk、d=limr{[logk-logNr(A)]/logr}=limr[logNr(A)/logr],式中r→0。
在实际计算中,可以根据需要使用一些边长为r的n维立方体(盒子),计算出不同r值的盒子覆盖A的个数Nr(A),然后在以-logr为横坐标、以logNr(A)为纵坐标的双对数坐标系中描出点(-logri,logNri(A)),最后利用最小二乘法拟合这些分布点的斜率便可以估计出集合A的盒维数。
1.4 木材声发射计数、声发射能量计算方法
在进行声发射计数之前,依据未加载时采集的信号,确定信号的时域阈值为40 dB。而声发射计数统计的是单位时间内声发射信号超过给定阈值的电信号数量。
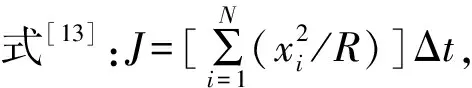
2 结果与分析
试验中,3组试件得到的数据在宏观统计特性上具有较高的相似性,因此本研究以试件ZZS-2的试验数据为例对试验结果进行分析讨论。试验中2个声发射传感器相对试件中部对称布置,经初步分析,2个传感器检测到的声发射信号数据在大小上虽有差异,但在表征木材损伤演变特征时具有较高的统一性,为避免长篇累牍,本研究取传感器S1检测到的声发射信号进行分析讨论。
2.1 木材声发射参数分析
本研究选取声发射计数、声发射能量,分析樟子松木材三点弯曲试验过程中载荷、声发射计数、声发射能量随时间的变化(见图2、图3)。结合载荷、声发射参数随时间的变化,并借鉴文献[14],可将木材的损伤过程大致分为线性阶段、非线性阶段、断裂阶段3个阶段。
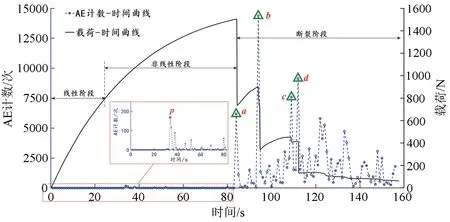
图2 木材声发射(AE)计数-时间-载荷曲线
线性加载阶段,根据CCD采集的实时图像可知,木材下沿的弯曲变形量极小,肉眼几乎无法分辨木材下沿是否弯曲,而此时载荷曲线仍保持线性;由此可以推测木材主要发生微观线性形变,此时产生的声发射信号幅值、能量极为微弱,远低于设置的声发射计数阈值(40 dB),这也是图2、图3中线性阶段声发射计数及声发射能量始终为0的原因。
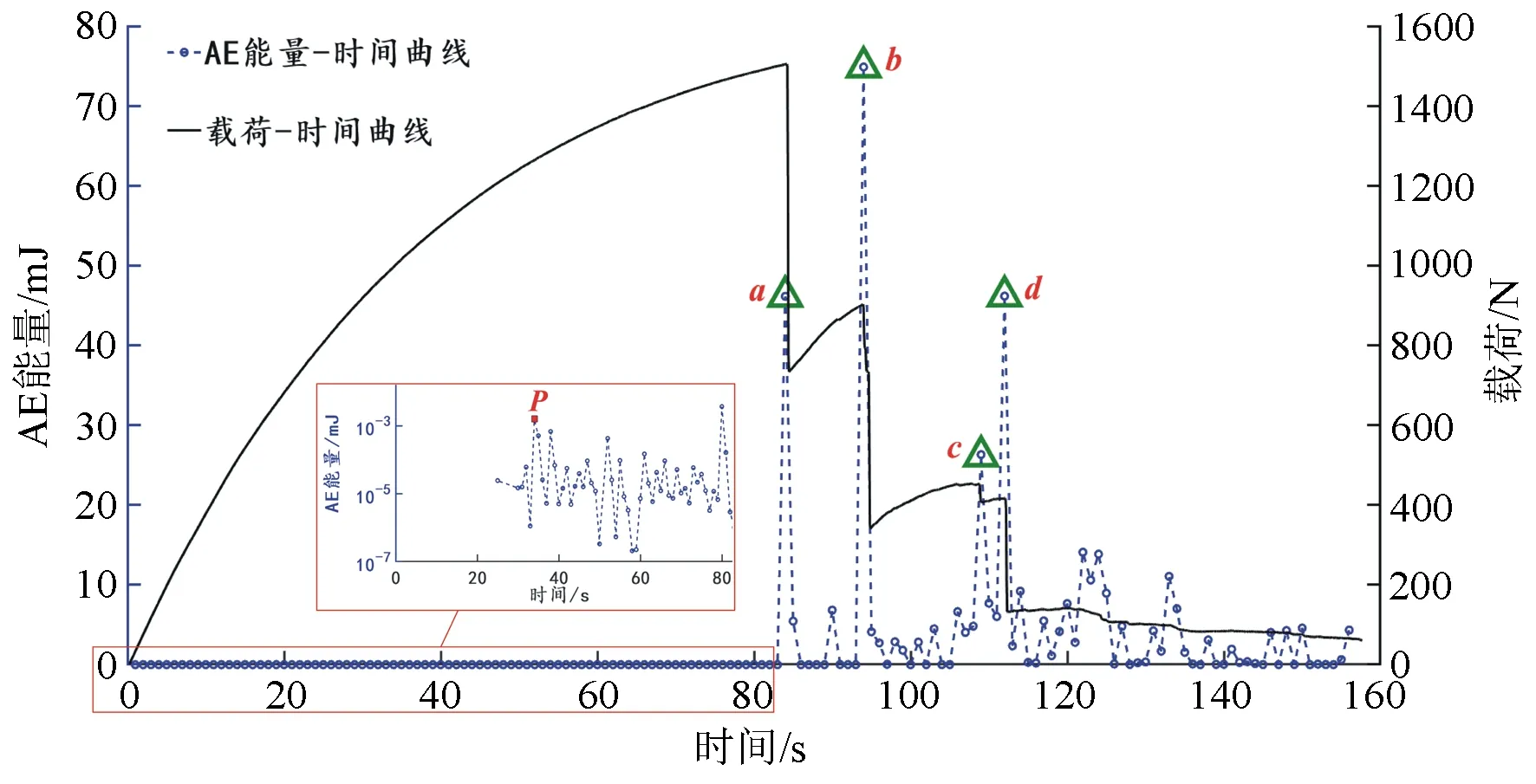
图3 木材声发射(AE)能量-时间-载荷曲线
由图2、图3可见:进入非线性变形阶段后,随着载荷的持续作用,声发射计数曲线、声发射能量曲线均出现小振幅振荡现象,说明木材内部逐渐出现不可逆的微观损伤,且声发射计数比声发射能量的突变更为显著。根据已有研究[6,14]可知,该阶段前期,由于木材抗拉强度及抗压强度的差异,导致了中性层出现偏移,从而出现少量的声发射现象;随着载荷持续作用,受拉的木质纤维素分子链之间剪切滑行加剧,而使胞间或胞壁层间出现微裂隙,从而出现较为丰富的声发射现象。尤其是图2、图3中的P点,对应的声发射计数、声发射能量在局部区间均达到1个较高的水平;说明前期不可逆的损伤积累,在该时刻达到了木材局部区域的强度极限,导致了微观损伤的形成。因此,P点可以认为是木材内部微观损伤的起裂点。
当加载到极限载荷,试件达到临界状态时,极其微小的扰动也会影响整个系统,形成“雪崩式”突发性失稳[15]。所以当载荷达到试件所能承载的载荷极限,继续加载后便导致了试件的突然破坏,发生显著的断裂现象;由图2可见:载荷“断崖式”下降,标志着木材由非线性变形过渡宏观断裂阶段。由图2、图3可见:试件出现突发性失稳断裂后,材料出现应力波的集中释放现象,相应的声发射计数、声发射能量首次出现了高梯度突发性增长,形成局部峰值(见图2、图3中的a点)。根据实时采集的图像可知,该时刻试件表面开始出现了宏观裂纹;因此,从声发射角度看,这种高梯度突发性变化,可以作为试件失稳破坏和宏观裂纹产生的判断依据(即可以认为a点是宏观损伤的起裂点)。
由图2、图3可见:进入宏观断裂阶段后,试件失去了对高载荷的承受能力,但由于木材的多胞及纤维增强的多层胞壁结构而具有很强的抗断裂韧性,起裂后还具有一定抵抗载荷破坏的能力;因此,随着载荷的继续作用,载荷-时间曲线呈“阶梯式”下降。该阶段随着载荷的继续作用,原有裂纹发生缓慢稳定扩展,产生了丰富的声发射现象。特别是每一次的宏观损伤加剧,载荷出现明显的“断崖式”下降,积聚的能量达到较高水平并以瞬态弹性波的形式向外释放,声发射计数曲线、声发射能量曲线再次出现显著突增现象,形成局部峰值(见图2、图3中的b、c、d点)。借鉴文献[16],并结合本研究结果,宏观断裂阶段,声发射计数曲线、声发射能量曲线的突发性增长,可以作为试件宏观损伤显著性加剧的表征。
2.2 木材裂纹图像分形维数的演化特征
根据图2、图3分析,通过声发射特征可以有效明确试件在宏观破坏发生之前的结构健康情况,实现损伤的定性评价;但是试件发生宏观损伤后,这种定性评价对于试件的损伤机制及演化规律研究,表征意义不够明确。图2、图3中,声发射计数、声发射能量的突变幅度与构件能否继续作为工程承载结构无直接联系;a点位置,试件失去了既定载荷抵抗能力,构件已经不适用于工程承载场合;但是应变能释放强度最高的b点,仅仅表征了损伤加剧。而木材的各向异性导致木材断裂裂纹具有非常强烈的非均质性,体现了非线性特征,具有明显的分形规律,通过断裂表面的分形特征可以实现材料表观形貌的定量表征[11],为此,本研究进一步利用裂纹动态演化过程中的分形特征,分析试件的宏观断裂特性。以ZZS-2试件的图像为例,分别利用灰度处理和二值化处理进行图像预处理,并用盒维数法求解其分形维数(见图4)。
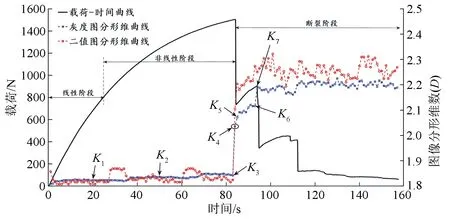
图4 木材裂纹图像分形维数-时间-载荷曲线
由图4可见:当处于线性和非线性阶段时,试件只有挤压变形,试件的灰度图分形维数与二值图分形维数约为1.83。当试件出现“雪崩式”突发性失稳时,试件表面宏观裂纹萌生,两种图像分形维数都出现显著性增长。到断裂阶段,两种图像分形维数都增长到2.2左右,尽管出现小幅度的波动振荡,但是整体上呈现逐渐增加的趋势。相比之下,二值图像分形维数曲线整体上表现出更为明显的振荡;而灰度图像分形维数曲线表现较为平滑,整体具有较高的稳定性,更符合裂纹增长趋势的变化。
图5中(a)~(g)为对应图4中K1~K7时刻的裂纹扩展及灰度图像分形维数情况。
图5(a)为试验20 s时试件受载的图像,此时木材处于线性阶段,试件下沿无明显弯曲变形,对应的灰度图像分形维数是1.823。
图5(b)为对应图4中K2时刻,木材处于非线性阶段,观察其受载图像发现,木材下沿有轻微弯曲但无裂纹,分形维数为1.836。
图5(c)为试验83 s时试件受载的图像,属于非线性变形和宏观断裂的临界状态,试件在载荷作用下发生变形,试件表面无肉眼可辨识的裂纹产生;根据声发射计数曲线、声发射能量曲线变化可知,该阶段试件内部已存在微观损伤,对应表面灰度图像分形维数是1.842。
图5(d)对应图4中K4时刻(84 s),试件在极限载荷的作用下发生突发性失稳,内部微观损伤进一步扩展,在试件表面孕育萌生了1条沿试件厚度方向演变的不规则宏观主裂纹,且图像分形维数直线上升至2.036,说明裂纹与分形维数相关联。
图5(e)对应图4中K5时刻(85 s),试件进入了宏观裂纹损伤扩展阶段,试件表面宏观主裂纹的存在进一步降低了结构的承载能力,使得试件在较低应力水平下发生裂纹尖端扩展。与84 s相比较,此时试件表面的宏观裂纹更清晰可见,除了原有沿试件厚度延伸的主裂纹进一步扩展外,还形成了1条沿试件轴向演变的新裂纹,此时图像分形维数进一步增加至2.072。分析85~92 s的图像可知,在宏观裂纹萌生以后,随着载荷作用,裂纹的扩展表现为孔洞间隙不断积累扩大[17],且无新裂纹的产生。
图5(f)为试验93 s的裂纹图像,与K5时刻相比,此时的裂纹仅仅出现间隙扩大现象,并未出现任何新的裂纹成核扩展,对应的灰度图像分形维数为2.116。
图5(g)为试验94 s的裂纹图像,此时的裂纹以在原来裂纹基础上产生了新裂纹连接各个裂纹孔洞,其灰度图像的分形维数为2.194。
由此可得:裂纹从无到有再到扩展,裂纹图像分形维数在增加。分析剩下的95~157 s的裂纹图像发现,宏观裂纹的扩展规律为:裂纹瞬间萌生以后,其向前扩展是间断进行的,先表现为孔洞间隙的积累扩大,当裂纹间隙扩大到一定程度,在某个瞬间又产生连通的新裂纹,以此反复地交替进行裂纹的扩展,对应的分形维数小幅波动。
根据上述的分析可知,试件在进入宏观断裂损伤后,试件的断裂特征与表面裂纹的分形特征之间存在良好的对应表征作用。对比3组试验中两种图像的分形维数(见表1),结果表明:用两种图像处理方式处理试件图像后计算得到的分形维数总体趋势一致,在线性和非线性阶段都基本持平在同一水平线;到断裂阶段,分形维数都上升至2.2~2.3,且两种不同的图像计算的分形维数的阶段性均值误差在0.1范围内。说明不管使用试件灰度图像或者是试件的二值图像的分形维数,都可以作为木材三点弯曲损伤断裂特征的表征,展示其宏观断裂裂纹的产生和扩展规律。
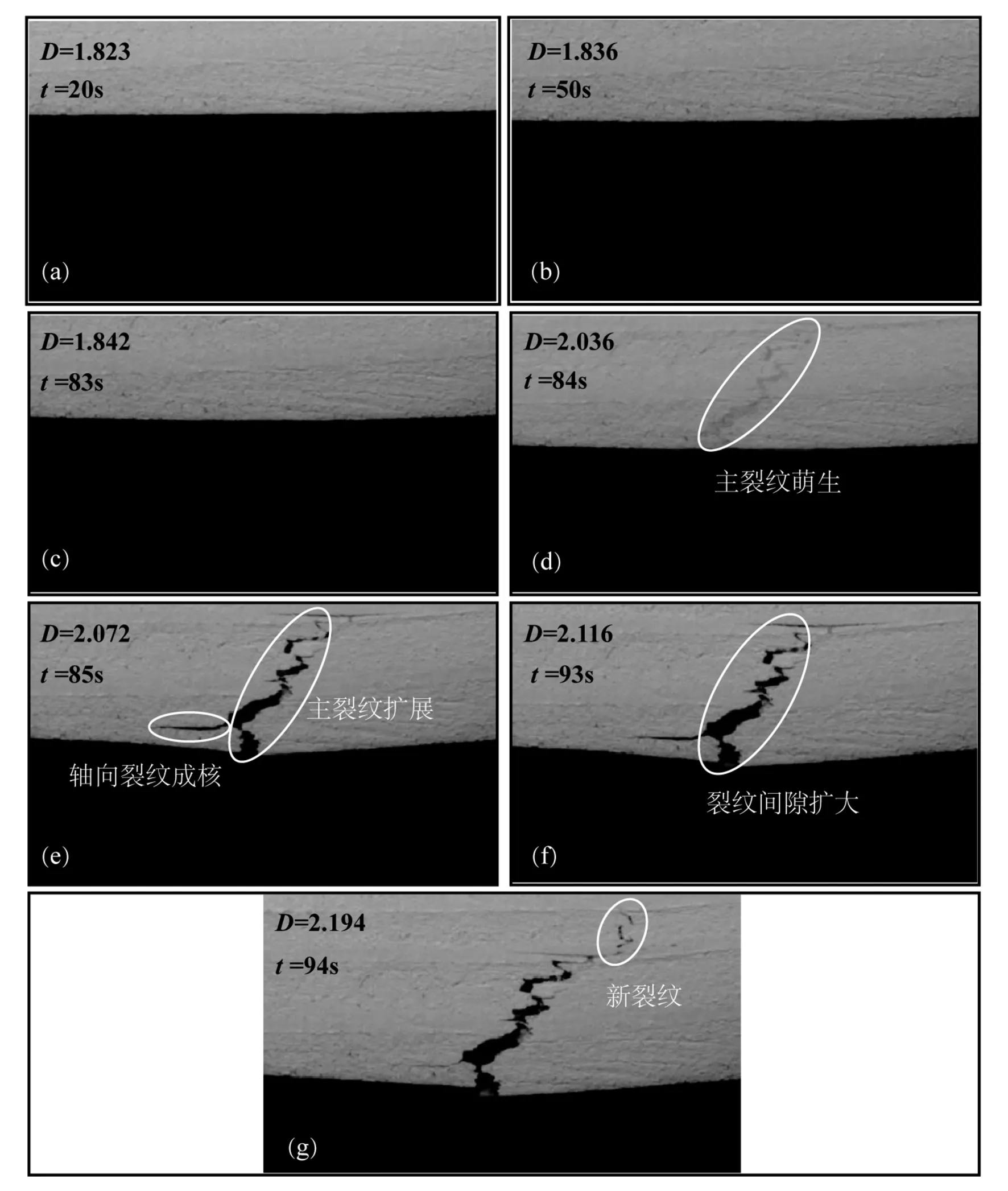
(a)~(g)为对应图4中K1~K7时刻的裂纹扩展及灰度图像分形维数;D为木材裂纹图像分形维数;t为试验时间。
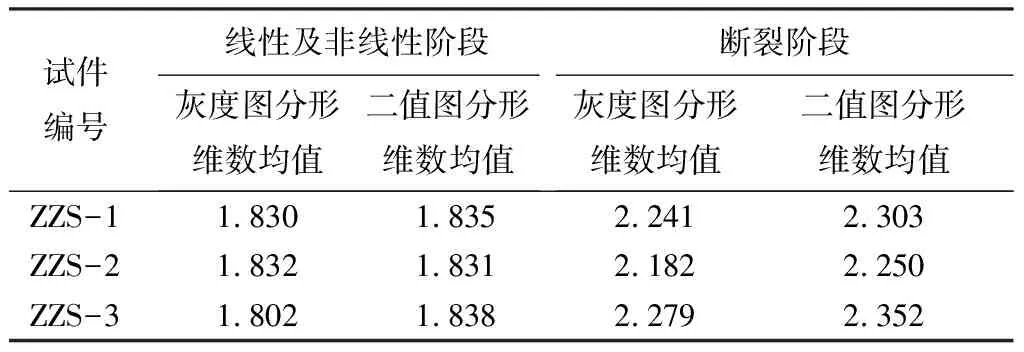
表1 木材裂纹灰度图像与二值图像分形维数
3 结论
对木材损伤过程的声发射信号进行处理分析,进入非线性变形阶段后,随着载荷的持续作用,声发射计数曲线、声发射能量曲线均出现小振幅振荡现象,说明木材内部逐渐出现不可逆的微观损伤。宏观断裂阶段,声发射计数曲线、声发射能量曲线的突发性增长,说明试件宏观损伤显著性加剧。
通过分析试件损伤断裂过程中图像的盒计数维数,在线性和非线性阶段,图像分形维数基本保持在同一水平;到试件断裂产生宏观裂纹,图像分形维数立即上升,且随着裂纹间断性扩展规律而变化,总体呈上升趋势。
结合声发射技术和图像分形,能综合反映木材内部的损伤演化过程以及木材表面裂纹的产生与扩展规律,可实时监测木构件损伤断裂过程中裂纹的发展。
