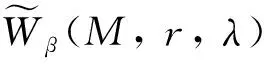模糊数列关于序β几乎理想λr-统计收敛和强几乎理想λr-收敛①

冯雪

青海民族大学 数学与统计学院， 西宁 810007

文献[1]提出了统计收敛的概念， 随后文献[2-9]对其进行了深入研究． 在实际问题中， 数据和信息往往是不确定的， 而这种不确定性可以用模糊数[10]来表示， 所以对模糊数列收敛问题的研究显得非常必要． 文献[11]提出了模糊集合和模糊集合运算的概念， 标志着模糊数学的诞生， 开创了模糊系统与模糊控制理论的研究． 文献[12]讨论了模糊数列的统计收敛， 并将模糊数列的统计收敛用自然密度为0的模糊数列和普通收敛的模糊数列来表示． 文献[13]给出了理想的定义， 提出并讨论了模糊数列的理想收敛． 文献[14]开始研究Orlicz序列空间， 结果表明任何一个Orlicz序列空间lM包含一个同构于lp(1≤p<∞)的子空间． 之后， 文献[15-16]分别利用Orlicz函数推广了Orlicz序列空间lM和强可和序列空间．

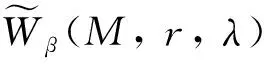
1 定义及说明

u为实数集R上的模糊集， 若u是正规的凸模糊集， 隶属度函数u(x)上半连续， 且支撑集

[u]0=cl{x∈R：u(x)>0}

为紧集， 则称u为模糊数[17]． 记所有模糊数所组成的集合为E1． 对任意的0≤r≤1， 水平截集[u]r={x：u(x)≥r}是一个闭区间． 对u，v∈E1，k∈R， 加法和数乘分别定义为

[u+v]r=[u]r+[v]r[ku]r=k[u]r

模糊数u，v∈E1之间的距离定义为

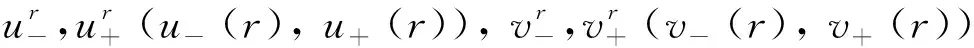
记N是全体自然数组成的集合， 集合A⊆N的自然密度定义为

其中|A|表示A的元素个数[19]．

设λ={λm}是非降数列，M是Orlicz函数，r={rk}是正实数列． 对于ρ>0， 0<β≤1， 模糊数列x={xk}关于序β几乎λr-统计收敛于模糊数x0， 是指[19]

其中

定义1设λ={λm}是非降数列，M是Orlicz函数，r={rk}是正实数列， 对于ρ>0， 0<β≤1， 模糊数列x={xk}关于序β几乎理想λr-统计收敛于模糊数x0， 是指

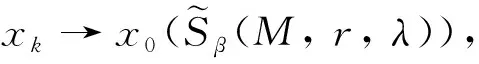
其中

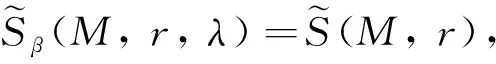
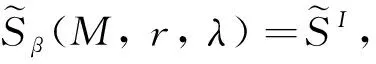
例1设I是自然密度0的自然数集N的理想，A={12， 22， 32， …}， 定义模糊数列

定义模糊数

当m∈A时， 有

即对任意给定的δ， 存在M， 使得对任意k>M，m∈A， 有

当m∉A时， 有

即

所以{xk}为几乎理想λr-统计收敛数列． 由以上讨论可知， 当m∉A时，

从而数列{xk}非统计收敛．

定义2设λ={λm}是非降数列，M是Orlicz函数，r={rk}是正实数列． 对ρ>0， 0<β≤1， 定义下列关于序β强几乎理想λr-收敛的模糊数列空间：

其中

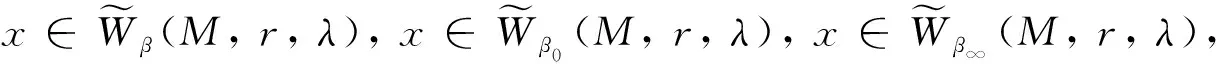
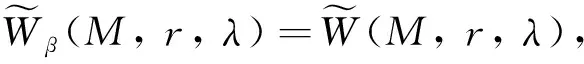
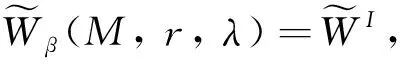
2 模糊数列关于序β几乎理想λr-统计收敛的相关性质

定理1设x={xk}，y={yk}是两个模糊数列， 则：

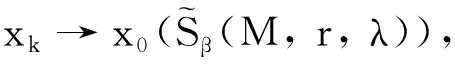
证(i) 当C=0时， 结论显然成立． 设C≠0， 有

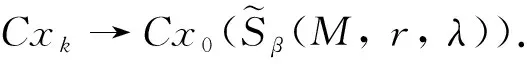
对于任意的ε>0， 有

可得

定理2设模糊数列x={xk}与关于序β几乎理想λr-统计收敛的模糊数列y={yk}几乎处处相等， 则x={xk}关于序β几乎理想λr-统计收敛， 而且与y={yk}收敛于同一模糊数．

证因为xk=yk几乎处处成立， 所以集合{k∈N：xk≠yk}有限， 设为S=S(ε)． 则

所以

因此模糊数列x={xk}关于序β几乎理想λr-统计收敛．

3 模糊数列关于序β强几乎理想λr-收敛的相关性质

定理3设λ={λm}是非降数列，M是Orlicz函数，r={rk}有界， 则

证显然

设

则

其中

存在K=δ， 使得

定理4设M1，M2是Orlicz函数， 则以下结论成立：

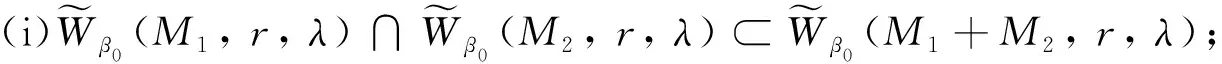
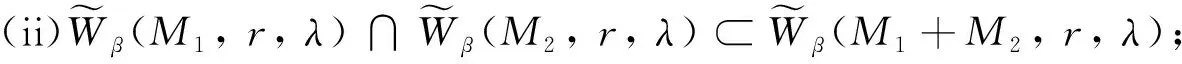
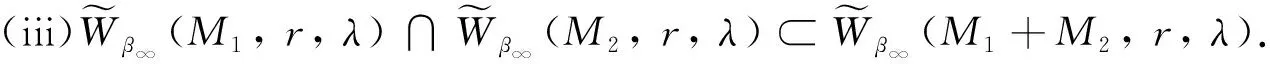
证(i) 设

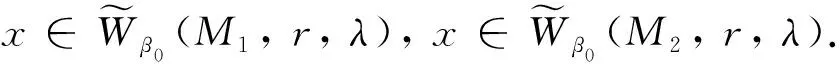
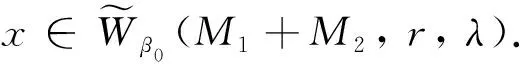
(ii)，(iii)的证明与(i)相似．

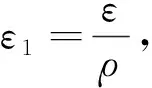
则

其中

K=min{[M(ε1)]h， [M(ε1)]H}

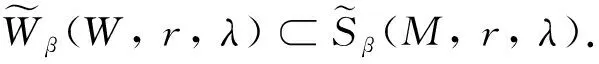
证记

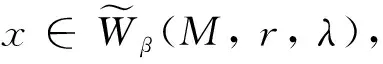
因为

所以

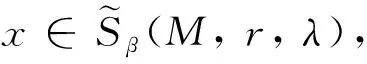
5 结论