基于热重启学习率的NAG算法在图像分割中的应用

陈甦欣, 晏文彬, 吕华鑫

(合肥工业大学 机械工程学院,安徽 合肥 230009)

随着我国科学技术的不断发展,计算机视觉技术和图像处理需求越来越突出，其中图像分割是图像处理中最基础的环节。图像分割是指为了识别和分析目标对象,根据灰度、形状以及纹理等特征的不同,将它们从复杂背景中提取和分离出来的过程。近年来各种图像分割方法被提出,其中基于变分水平集的活动轮廓模型不仅可以有效处理拓扑结构的变化,而且能够在分割过程中保持曲线的连续性和光滑性,成为近年研究热点。水平集分割的基本思想是:首先根据图像特征为演化曲线定义一个能量泛函,为了极小化该能量泛函,常通过变分法和梯度下降法得到控制水平集演化的偏微分方程；然后用数值求解方法解此方程,方程的数值解即为所要的分割曲线[1-5]

随着智能化设备的逐渐普及,图像分割在医学影像检测系统、交通控制系统以及视频目标监控跟踪等领域均有应用,此时图像分割速度的快慢程度直接影响到后续的处理过程。然而,基于变分水平集的活动轮廓模型由于其极小化过程中所使用的梯度下降法收敛性较差[6-7],导致模型演化速度较慢,难以满足图像分割在实际应用时的实时性要求。

本文以Chan和Vese的基于区域的水平集模型Chan-Vese(CV)模型[8]与文献[2]的距离保持惩罚项为例,使用基于热重启学习率的Nesterov加速梯度(Nesterov accelerated gradient,NAG)算法代替演化过程中使用的梯度下降法,提出了一种快速图像分割方法。与CV模型原本的分割方法相比,该方法能够更快速地实现对图像的分割。在同样的初始条件下,本文算法对医学图像等复杂图像和一些轮廓比较分明的图像都能够准确且快速地得到分割结果。

1 建立具有距离保持项的CV模型

CV模型通过计算图像目标区域与背景区域的灰度信息来控制曲线的拓扑变化,使得复杂结构的目标得以准确分割且对初始轮廓有较高的鲁棒性。CV模型的能量泛函如下:

F(c1,c2,C)=μLength(C)+

νArea(inside(C))+

(1)

其中:μ≥0;ν≥0;λ1、λ2>0为每个能量项的权重系数；Length(C)为闭合轮廓曲线的长度；Area(inside(C))为曲线内部区域的面积；c1、c2为目标区域与内部区域的平均灰度值。

通过变分法和梯度下降法极小化能量泛函,得到控制水平集函数演化的偏微分方程，即

(2)

实际运用中,CV模型的演化公式在演化一段时间后会使水平集失去光滑性和距离函数的性质。为避免该问题,应在演化一定时间后对水平集函数重新初始化。由于重新初始化存在复杂时间成本,为了消除重新初始化的需要,结合一个距离保持惩罚项[9],形成新的演化方程如下:

(3)

由于增加了距离保持项,上述演化方程可以通过简单的有限差分进行数值实现，即

(4)

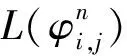
2 本文水平集演化方法

2.1 NAG演化算法

原始CV模型的水平集分割利用梯度下降法一步一步地改变水平集曲线,使得上文所述能量泛函极小化从而得到分割结果。而梯度下降法在演化时收敛较慢,并且极易陷入局部极小值，从而得到错误的分割。

NAG算法[10]的基本思想是在计算参数梯度时超前考虑后一步位置的梯度而不仅仅是当前位置的梯度,因此可以预先判断更新方向从而增加迭代的速度。NAG算法的公式如下:

di=βdi-1+g(θi-1-αβdi-1)

(5)

θi=θi-1-αdi

(6)

其中:β为经对上一次更新的衰减权重；α为学习率；g(θ)为目标函数在θ处的梯度。NAG算法的更新量考虑了往后一步θi-1-αβdi-1位置的梯度。NAG算法考虑了二阶导数,因而会比梯度下降法收敛得更快。NAG算法图解如图1所示。

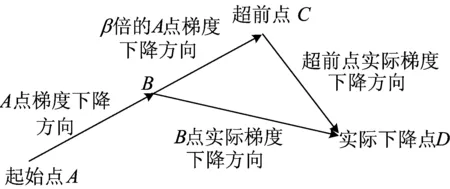
图1 NAG算法图解

2.2 热重启学习率

因为传统的梯度下降法和NAG算法学习率都是恒定的,在整个迭代过程中均以确定的步长来进行更新，所以存在2个不可避免的问题:① 若步长过大,则容易在最小值处反复地震荡从而无法有效地收敛;② 若步长过小,则会增加过多的迭代时间来达到收敛,而且在陷入陡峭的局部极小值时无法跳出。

为了解决固定学习率引起的上述问题,本文基于重启学习率和余弦退火的思想让学习率随迭代过程按照一定的余弦规律进行周期性变化,并且每隔一段时间重新设置初始值。为了更好地收敛,本文使用一种热重启的方式,即使得每次重启的间隔逐次递增,从而让快收敛时学习率不会再回升而是逐渐减小，从而准确收敛到最优解。

热重启学习率根据迭代次数变化的情况如图2所示。

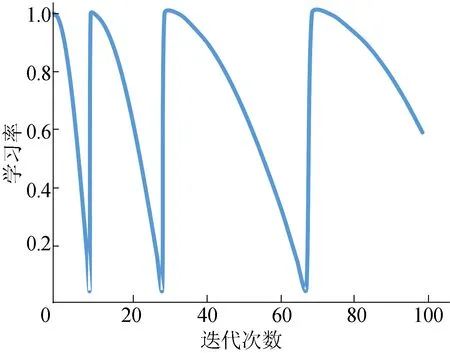
图2 热重启学习率图解

定义热重启学习率的公式如下:

(7)

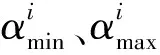
2.3 演化水平集方程

水平集方程中的各参数在本文演化算法中的定义如下:

(1) 水平集函数φ。视为NAG算法中的θ,通过不断更新θ来极小化能量泛函。

(3) 时间步长Δt。视为NAG算法中的学习率α,其值按照(7)式来定义。本文实验取Δt的最小值为0.02,最大值为1.0,初始值为1.0。

本文算法的主要参数设置选取为:能量项权重系数λ1=λ2=1,μ1=1,μ2=0.000 001×2552,ν=0。

2.4 分割算法流程分析

本文的分割算法流程如图3所示。

图3 本文分割方法流程

首先对图像进行一定的预处理,高斯平滑去噪,图像增强,提高对比度;然后建立水平集演化方程,编写演化过程代码。本文算法的演化实现过程如下:

(1) 设动态变化时间步长为Δt,Δt中使用上述的热重启公式来定义。通过鼠标交互函数手动框选选择合适的初始水平集函数φ0和初始速度ν0。

(2) 若达到停止准则(指定的迭代次数或者完全收敛),则终止算法；否则转步骤(3)。

3 实验结果评估分析

3.1 实验结果分割时间对比

本文实验中将使用梯度下降法与使用热重启学习率的NAG算法进行分割结果对比。用2种算法分别处理图像,比较其得到相同分割结果时的CPU处理时间。本文实验环境为:Windows10系统,Intel Core i7,16 GiB内存(RAM),实验平台为Visual studio 2017。使用了C++编程语言,调用了OpenCV库。

由于水平集分割适用性广,本文分别对不同形状的图像进行分割。本文算法对噪声图像、五角星图像和汽车图像进行分割的结果如图4所示。

图4 本文算法的不同形状图像分割

为了验证本文算法对复杂图像的分割效果,本文分别对肺部CT图像、血管图像和细胞图像进行了分割,分割结果如图5所示。

图5 本文算法的复杂图像分割

实验结果显示,本文算法的演化速度对比梯度下降法有较大提升,大大减少了迭代次数,并且几乎不会陷入局部极小值。2种算法的分割速度见表1所列。

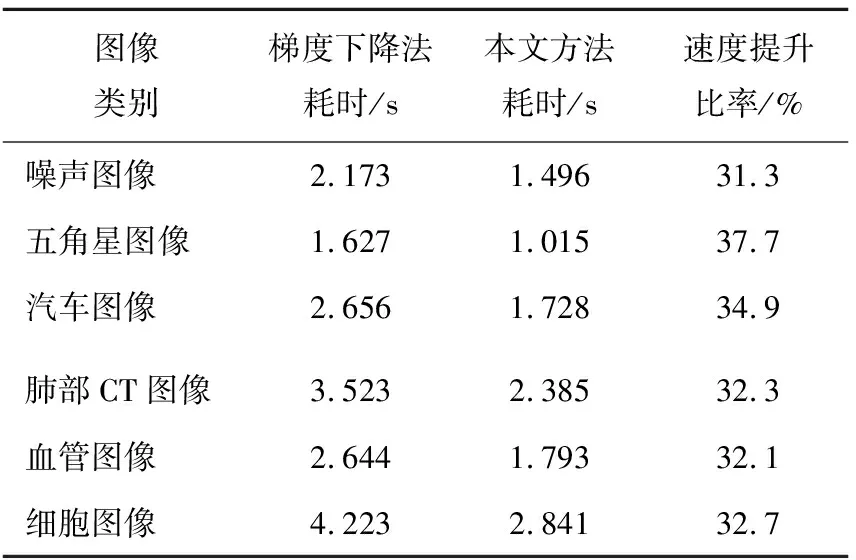
表1 算法分割速度对比

从表1可以看出,用改进后的NAG算法替代传统梯度下降优化方法,6张图片的分割速度均提升了30%以上,这说明用本文算法迭代水平集函数能够使图像分割在时效性上有较大的提升。

3.2 基于GT图像评估分割精度

分割结果的精确度是验证分割算法效果的主要准则,为了量化分割结果的精确程度,本文使用ground truth(GT)图像进行分割图像的结果评估。

为了获得直观的对比,本文使用手绘分割边缘的图像作为GT图像，将结果图像分别与对应GT图像计算相应的分割精度(分割准确像素点数占GT图像像素点数的比率),计算公式为:

(9)

计算过分割率(分割在GT图像参考面积之外的像素点的比率)和欠分割率(分割在GT图像参考面积之中欠缺的像素点的比率)。结果评估见表2、表3所列。

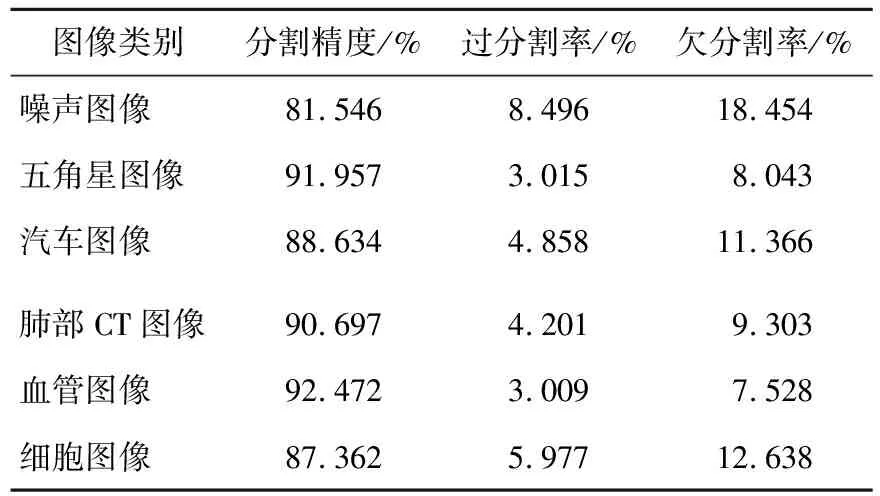
表2 梯度下降法实验图像结果评估

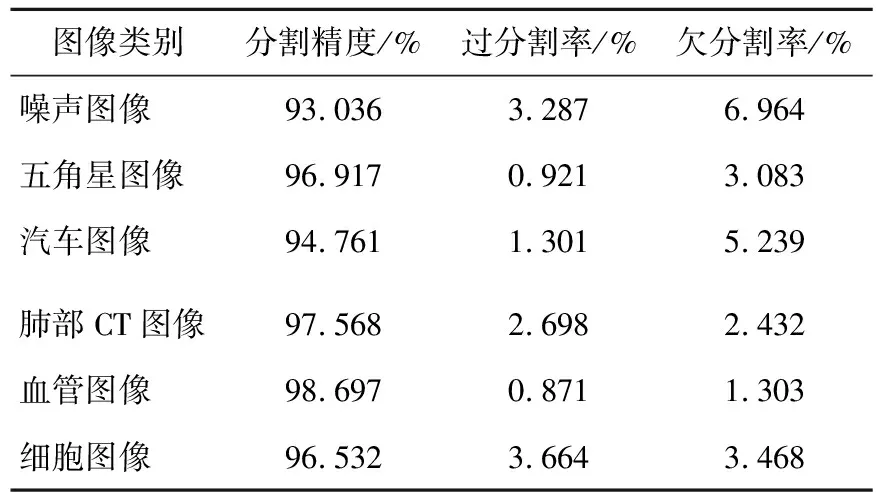
表3 本文方法实验图像结果评估

从表2、表3的数据对比可以看出,改进后的迭代算法对6张图像其中4张的分割精度在95%之上,相较于用传统的梯度下降法来进行分割迭代,使用热重启学习率后的NAG算法在图像分割准确度上有较大提升。

4 结 论

本文针对梯度下降法的收敛性差、易陷入局部极小值等特点,提出一种基于热重启学习率的NAG算法的图像分割方法,建立了带有距离惩罚项的CV模型,使用NAG算法替代梯度下降法对水平集函数进行演化,并且用热重启学习率的方法设置迭代步长。实验结果表明,基于热重启学习率的NAG算法来演化水平集函数相比梯度下降法能够有效地提高分割速度。对于不同形状的图像和复杂的医学图像等,本文的改进算法不仅能获得平滑的水平集曲线以及分割准确的结果图像,还缩短了超过30%的分割时间,能够更好地满足对图像分割实时性的要求。