基于AUKF的锂离子电池SOC估计方法*

王 萍，弓清瑞，程 泽，张吉昂

（天津大学电气自动化与信息工程学院，天津 300072）

前言

锂电池作为一种清洁能源，以其能量密度高、体积小、寿命长等优点，被广泛应用于电动汽车和电力系 统 等 诸 多 领 域。 电 池 管 理 系 统（battery management system，BMS）可以实现对电池的科学评估和风险预警，从而保证电池的稳定运行。电池荷电状态（state of charge，SOC）直接反映了电池的剩余电量，它的准确估计是BMS 运维的关键环节。然而SOC 并不能直接测量，只能通过电池的外部可测变量，结合数学算法来推断。

目前SOC 的估计方法主要有直接测量法、数据驱动法和基于自适应滤波器的方法。

直接测量法包括安时积分法和开路电压法。安时积分法是通过对放电过程中电流随时间积分来获得SOC。该方法有简单易用的优点，但十分依赖于SOC 初值的确定，且电流的测量误差会随时间累积。开路电压法是通过测量电池的开路电压（open circuit voltage，OCV），通过查询OCV-SOC 曲线来获得电池SOC。但该方法须将电池离线后进行长时间静置，因而难以用于SOC的在线估计。

数据驱动法是使用机器学习的算法建立电池外部可测变量如电压、电流和温度等参数与SOC 的映射关系。机器学习方法主要包括统计机器学习方法和神经网络的方法。其中，后者有更灵活的内部结构，对非线性关系的表达能力也更强，应用也更广泛。这类方法无须分析电池复杂的电化学反应，但计算量较大，且十分依赖于训练集的有效可靠。

基于自适应滤波的方法须建立等效电路模型，再结合滤波算法来实现SOC 的闭环估计。如文献［11］中使用2 阶RC 模型对锂电池进行建模，并结合模糊自适应卡尔曼滤波器来实现对SOC 的实时估计。常用的等效电路模型有PNGV 模型和RC 模型等。常用的滤波算法有观测器、粒子滤波器、卡尔曼滤波器等，其中卡尔曼滤波器最为常用，有着许多优秀的变型，如扩展卡尔曼滤波器、自适应扩展卡尔曼滤波器和无迹卡尔曼滤波器等。这类方法可以矫正SOC初始值不确定造成的误差和缓解过程中误差积累，但对等效电路的参数较为敏感。

无迹卡尔曼滤波器（unscented Kalman filter，UKF）因其优越的性能被广泛应用。但UKF 存在对电池模型精度和系统噪声的要求较高，稳定性不强的问题。针对该问题，本文中引入一般性的滤波器收敛判据，从自适应调整测量噪声、调整过程噪声和修正卡尔曼增益的角度改进UKF，形成了基于自适应无迹卡尔曼滤波器（adaptive unscented Kalman filter，AUKF）的SOC 估计方法。本文利用测试数据和马里兰大学电池数据集进行了实验，结果表明所提方法具有较快的收敛速度和较高的估计精度。

1 RC等效电路模型

RC 等效电路模型结构简单，只需少量的参数和较低的计算成本便可完成建模，应用广泛。本文以2阶RC 模型为例，展示电池建模和SOC 估计的过程，模型结构如图1所示，其状态空间数学表达式为

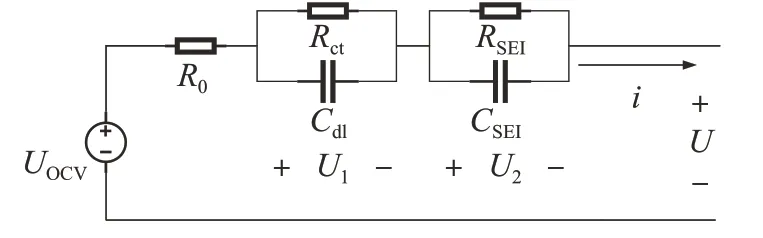
图1 2阶RC模型的结构

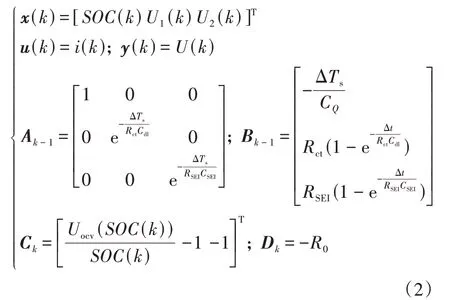
式中：表示电池端电流；代表电池端电压；表示电池的欧姆内阻；和并联环节表示电化学极化过程，和并联环节表示浓度差极化过程；表示电池的开路电压。

本文通过离线实验对RC 模型阻容等参数进行辨识，具体包括（·）、、、、和。

2 参数辨识

2.1 CCP测试

本文的实验对象是额定容量为3 A·h、标称电压为3.6 V 的18650 三元锂离子电池。设定恒温箱温度为25 ℃，采用恒流脉冲（constant current pulse，CCP）测试进行参数辨识，实验步骤如下：

①将室温下充满电的电池置于恒温箱内，静置1 h，记录电池的开路电压；

②以1C恒流放电3 min；

③静置2 h，记录电池的静置电压；

④重复过程②和③直至电池放空。

CCP 实验的电压和电流全周期和一个周期的变化曲线如图2和图3所示。

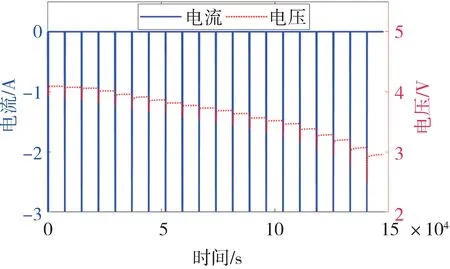
图2 CCP测试全周期曲线图

图3 中A 点之前电池处于静置状态；在BC 段，以1C 放电3 min，电压快速下降，SOC 下降0.05；在DE 段，电池静置2 h，电流为0，电压缓慢回升，并逐渐趋于稳定。

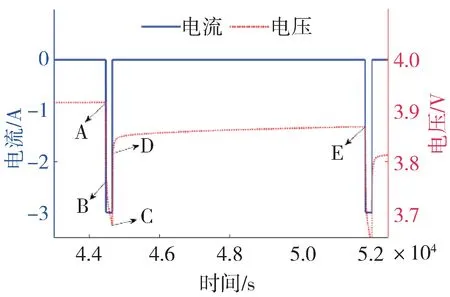
图3 CCP测试一个周期曲线图

2.2 OCV-SOC曲线拟合

在CCP 测试第③步中，取静置结束时刻的E 点电压值作为当前SOC 下的OCV 值。CCP 测试过程共得到20 个SOC-OCV 散点。本文将电化学模型Shepherd、Unnewehr 和Nerst 进行组合，得到一种较为理想的开路电压模型，如式（3）所示，使用最小二乘法来对其进行拟合，从而得到各参数的辨识值。

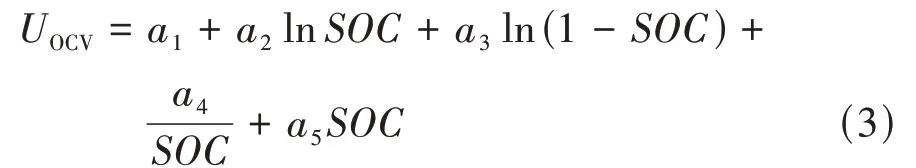
2.3 阻容参数辨识

2.3.1的辨识

分别计算通电瞬间（AB 段）和断电瞬间（CD 段）的后，取二者的平均值作为最终值，计算式为

式中Δ和Δ分别为通电和断电瞬间电压变化的绝对值，分别对应图3 中AB 段的电压骤降和CD段的电压骤升。

2.3.2、、和的辨识

DE 段可看作是RC 环节的零输入响应。D 为起点，电容和两端初始电压分别为（0）和（0），这时端电压表达式如式（5）所示。使用最小二乘法对式（5）进行拟合，可以得到（0）、（0）以及时间常数、的值。

BC 段可看作RC 环节的零状态响应。因为电容电压不能突变，由C 点和D 点的极化电压相等的关系可得

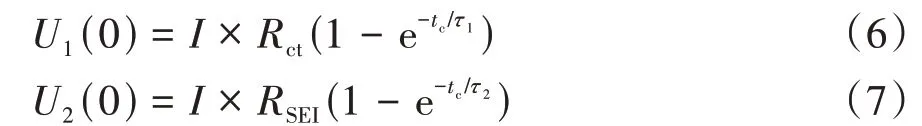
式中=3 min。

由式（6）和式（7）可计算得到和，进一步由=×的关系可得和。

RC 模型的阻容参数会随SOC 的变化产生波动，使用线性插值法来拟合这种波动，即

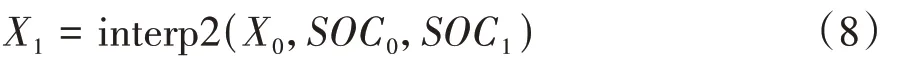
式中：=｛0.95，0.9，...，0｝；X为对应的参数取值序列；为某个实际的SOC 值。Interp2 表示2 维线性插值运算，即在与距离最近的两个参考点之间建立线性模型，将代入获取此时的参数值。

3 AUKF算法

3.1 UKF算法

UKF 算法主要包括系统初始化、状态预测和测量校正3个部分。

（1）系统初始化

初始化状态量和误差协方差矩阵为

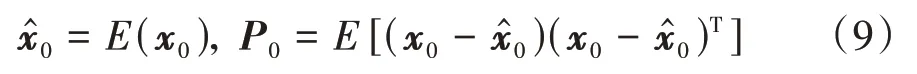
用对称采样法生成初始Sigma点，其中为尺度参数：

（2）状态预测

第个采样时刻，Sigma点构建的矩阵为

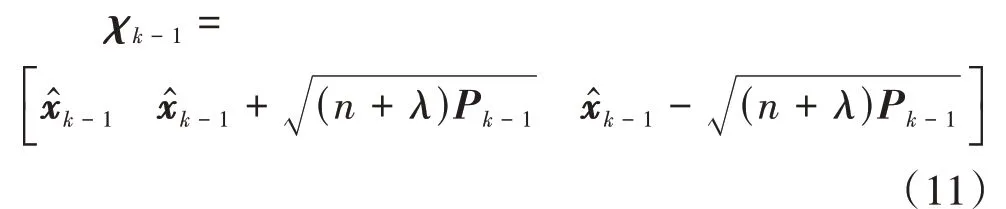
对式（11）的Sigma点进行状态方程的处理，并对时刻系统状态量和误差方差矩阵进行预测：

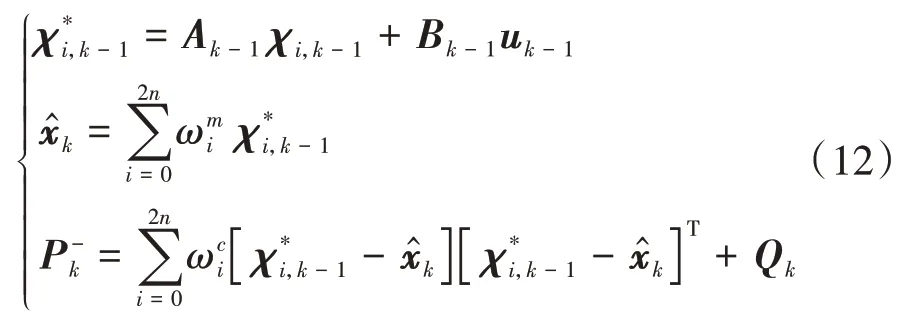
式中Q为时刻的过程噪声协方差矩阵。

（3）观测校正

计算时刻的观测量的估测值：

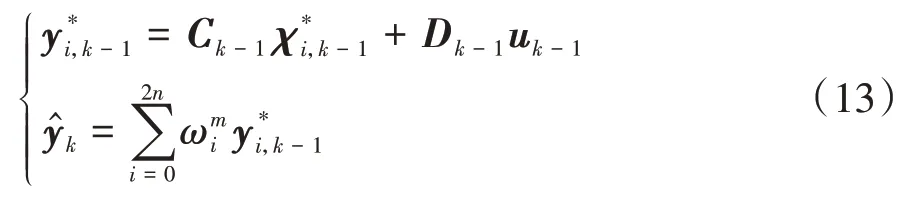
计算时刻观测量的方差矩阵为

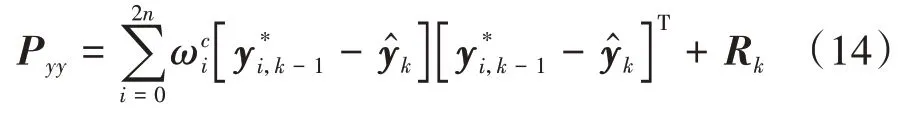
式中R为时刻的测量噪声协方差矩阵。

计算时刻状态量与观测量的协方差为

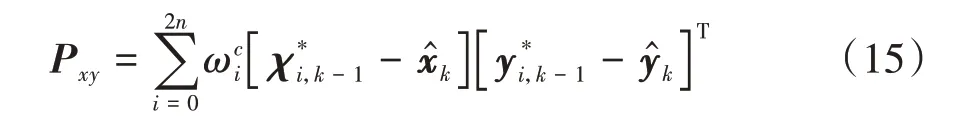
计算卡尔曼滤波增益为

更新状态量与误差方差矩阵为

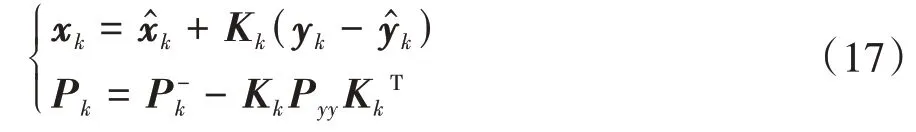
3.2 AUKF算法的实现

UKF算法能够实现对系统状态的实时估计。但仍存在以下问题：

（1）由于在非线性系统中存在一些不确定因素，导致过程噪声协方差矩阵Q和测量噪声协方差矩阵R难以获得准确值。而使用经验法将它们设置为定值则会影响UKF的估计精度。

（2）UKF对RC模型的精度十分依赖，但RC模型的阻容参数辨识存在误差是不可避免的。当模型误差较大和R取值不当时，会通过测量校正环节引入较大的状态估计误差。

（3）实际应用中常存在SOC 初值存在偏差和测量噪声异常扰动等突发情形。常规的UKF 对这些情形的自适应能力较有限。

3.2.1 测量噪声协方差自适应调整

设置越大，表明对测量值的置信度越低，这会导致算法初始的收敛速度慢；设置越小，收敛速度越快，但会导致SOC 估计后期的波动性较大。可见过大或过小的值都会影响SOC 的整体估计效果。因此在滤波算法的初始阶段设置较小的值，用表示，使SOC的估计初值快速向真实值方向收敛，等到估计值收敛到真实值附近时，再切换较大的值，用表示，以降低估计值的非线性波动。和的取值与电压传感器的测量精度有关，所以在SOC 估计的初始阶段，的取值比电压传感器精确度低一个数量级，过小容易引起估计值波形在起始阶段过冲。则取比传感器精度高一个数量级的数，过大则会引起值减小，使测量校正失去作用。

根据文献［21］中提出的滤波器收敛性判据，滤波器发散时，真实的估计误差要远大于计算得到的预测误差。因此，SOC估计的发散条件为

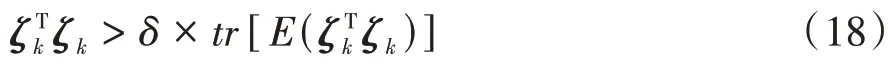
在后续SOC 的估计过程中，能通过影响增益，进而影响SOC 估计的测量校正阶段。当传感器测量误差较大或RC 模型的误差较大，即时刻的观测残差ζ较大时，如果此时值非0，会在测量校正阶段引入较大的估计误差。因此为该算法设置第2个判据：

若式（20）不满足，即观测残差ζ超过预设阈值时，则将设为无穷大，此时趋于0，相当于只进行状态预测而不进行观测校正，只有当测量误差较低和RC模型精度较高时，才同时进行状态预测和观测校正。判据式（20）的引入，有助于降低UKF对RC模型精度和传感器测量精度的依赖，增强SOC 估计的稳定性。

3.2.2 卡尔曼增益自适应调整

3.2.3 过程噪声自适应调整

过程噪声主要反映系统模型的误差。通过在SOC估计的过程中动态调整，使其能充分反映系统模型本身的误差，以避免模型误差造成的SOC 估计精度过多的下降。方法是通过利用多个之前时刻的真实值与估计值的残差，对下一时刻的Q进行递推：

式中：-<<；e表示在-1～区间内，由电压测量值与模型估计值的残差组成的序列；G表示由e组成的协方差阵；表示该e序列的长度，该值越大，越能充分反映系统的模型误差，但是计算量也越大。Q由式（24）不断迭代递推获得。

通过在SOC 估计过程中对测量噪声协方差、卡尔曼增益和过程噪声协方差进行自适应调整，形成了AUKF算法，如图4所示。

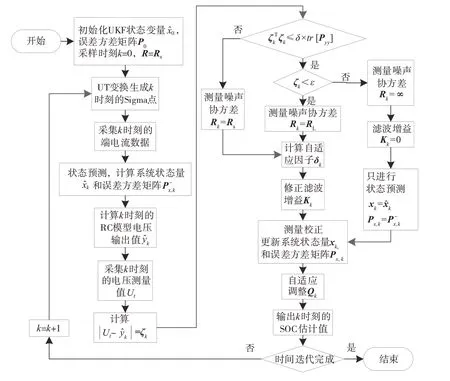
图4 AUKF算法流程图

4 实验与分析

利用实际测试数据和马里兰大学电池数据集，对所提出的AUKF算法的性能进行验证。

4.1 实验测试数据

设置恒温箱温度为25 ℃，对额定容量为3 A·h、标称电压为3.6 V 的18650 三元锂离子电池充满电后，采用动态应力测试（dynamic stress test，DST）工况进行放电，放电过程中电池的电压电流曲线见图5。

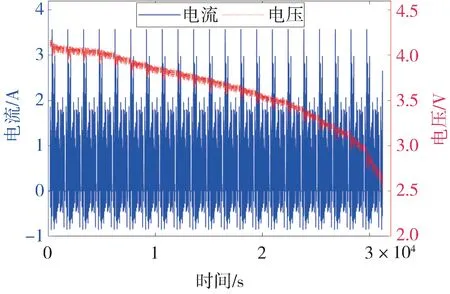
图5 DST工况下电压电流测试曲线

图6展示了采用AUKF 和UKF 算法进行SOC 估计的结果和相对误差，图7 为采用AUKF 算法进行SOC 估计过程中的电压观测值和模型输出值、拟合误差即残差随放电时间的变化情况。由图6 可知，UKF 算法收敛后的相对误差在3%以内，而AUKF 算法收敛后的相对误差则更小，接近于零，且具有更快的收敛速度，更高的估计精度，估计值曲线更加平滑和稳定。图6 和图7 右图的绿色虚线表示发散与收敛的界限：在它之前的时刻，由于SOC初始误差的存在，端电压的拟合残差也存在较大偏差，这时式（19）成立，滤波器处于发散状态，此时选取较小的作为测量噪声协方差，之后的时刻AUKF 收敛，选取较大的作为测量噪声协方差。图7右图的红色和蓝色虚线分别表示电压正阈值和负阈值，阈值设为0.03 V。在滤波器收敛后的SOC 估计过程中，由于传感器测量精度或RC 模型本身的误差造成一些时刻的观测残差大于阈值，则这些时刻的设为无穷大，只进行状态预测而不进行状态校正。

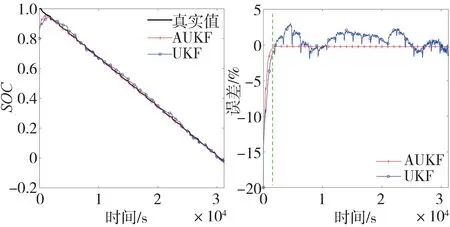
图6 SOC估计结果与误差（SOC0=0.8）

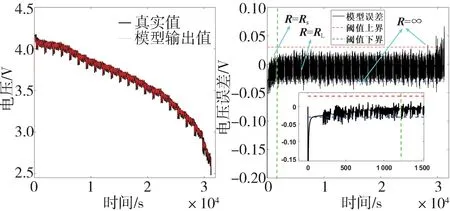
图7 电压观测值、模型输出值和残差的时间历程（SOC0=0.8）

为定量刻画算法的收敛性能，定义“跟随系数”为SOC 真实值与估计值的误差绝对值小于0.02 所用的时间与放电总时间的比值。表1 列出跟随时刻之后的平均绝对误差（mean absolute error，MAE）和均方根误差（root mean squared error，RMSE）及跟随系数。

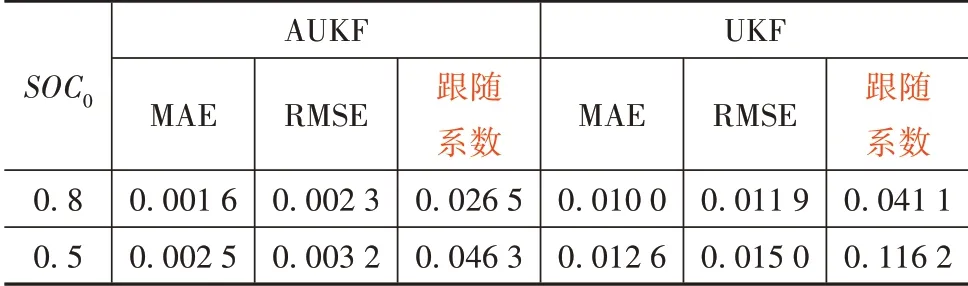
表1 SOC估计误差和跟随系数

为进一步验证不同的SOC估计初值对两种算法的影响，取=0.5，得到图8 和图9。由仿真测试结果可知，取较小的SOC估计初值时，两种算法下的收敛时间均会变长，跟随系数都有所增加，图8 和图9 的绿色虚线也更加靠右。其中UKF 的跟随系数增加幅度更大，表明UKF 算法抵抗初值不确定性的稳定性较差。虽然AUKF 算法的估计误差与初值为0.8 时相比略有增加，但估计误差MAE 与RMSE 仍保持在较低水平。

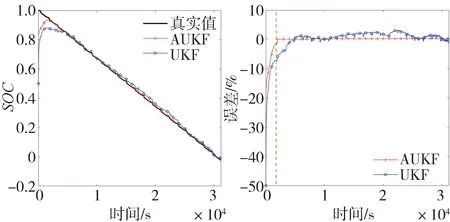
图8 SOC估计结果与误差（SOC0=0.5）

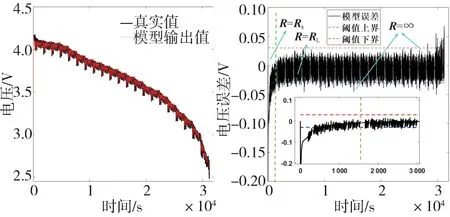
图9 电压观测值、模型输出值和残差的时间历程（SOC0=0.5）

为进一步验证所提出的AUKF 算法对不同SOC初值的收敛能力，取为0.2、0.4、0.6 和0.8 进行仿真测试，得到结果如图10 所示。估计误差和跟随系数列于表2 中。可知不同SOC 估计初值下，AUKF 均能可靠收敛，跟随系数都保持在0.07以内。随着初始误差增大，跟随系数升高，总体MAE 和RMSE 误差增大，但最大值都不超过1%。这表明所提出的AUKF 算法具有较高的估计精度和较好的鲁棒性。

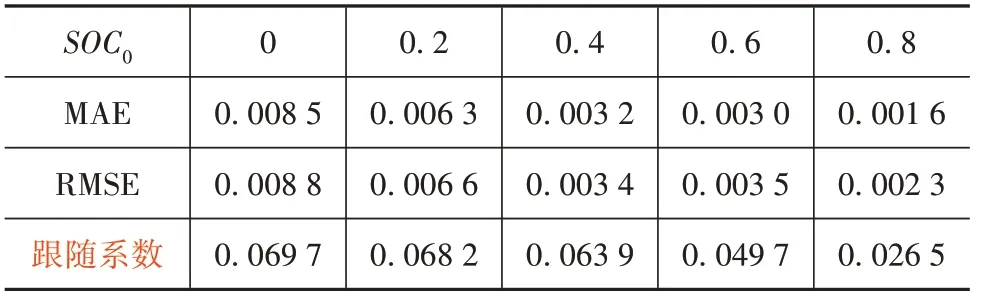
表2 不同SOC估计初值下的计算误差和跟随系数

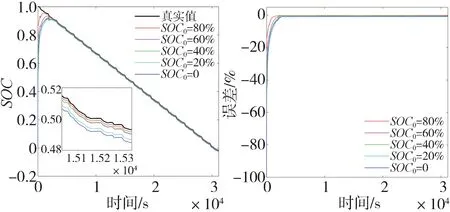
图10 不同SOC估计初值下的估计效果与误差

4.2 马里兰电池数据集

马里兰大学电池数据集使用额定容量为2 A·h、标称电压为3.6 V 的18650 三元锂离子电池进行试验。该数据集中提供了电动汽车常用的测试工况数据，如US06 工况、联邦城市行车（federal urban driving schedule，FUDS）工况、北京动态应力测试（Beijing dynamic stress test，BJDST）工况。因此，该数据集很适合验证本文提出的基于AUKF 的SOC 估计方法。需要注意的是，该数据集中的测试电池是从约80%额定容量时开始放电，在约为20%额定容量时放电结束，该放电区间也是电动汽车实际应用中最常用的放电区间。取=0.6，各动态工况的SOC 估计结果和误差分别如图11～图13 所示，其MAE 和RMSE 计算误差与跟随系数列于表3 中。可以看到，在3种不同测试工况下，与UKF相比，AUKF具有更小的跟随系数和估计误差，表现出更加优越的性能。

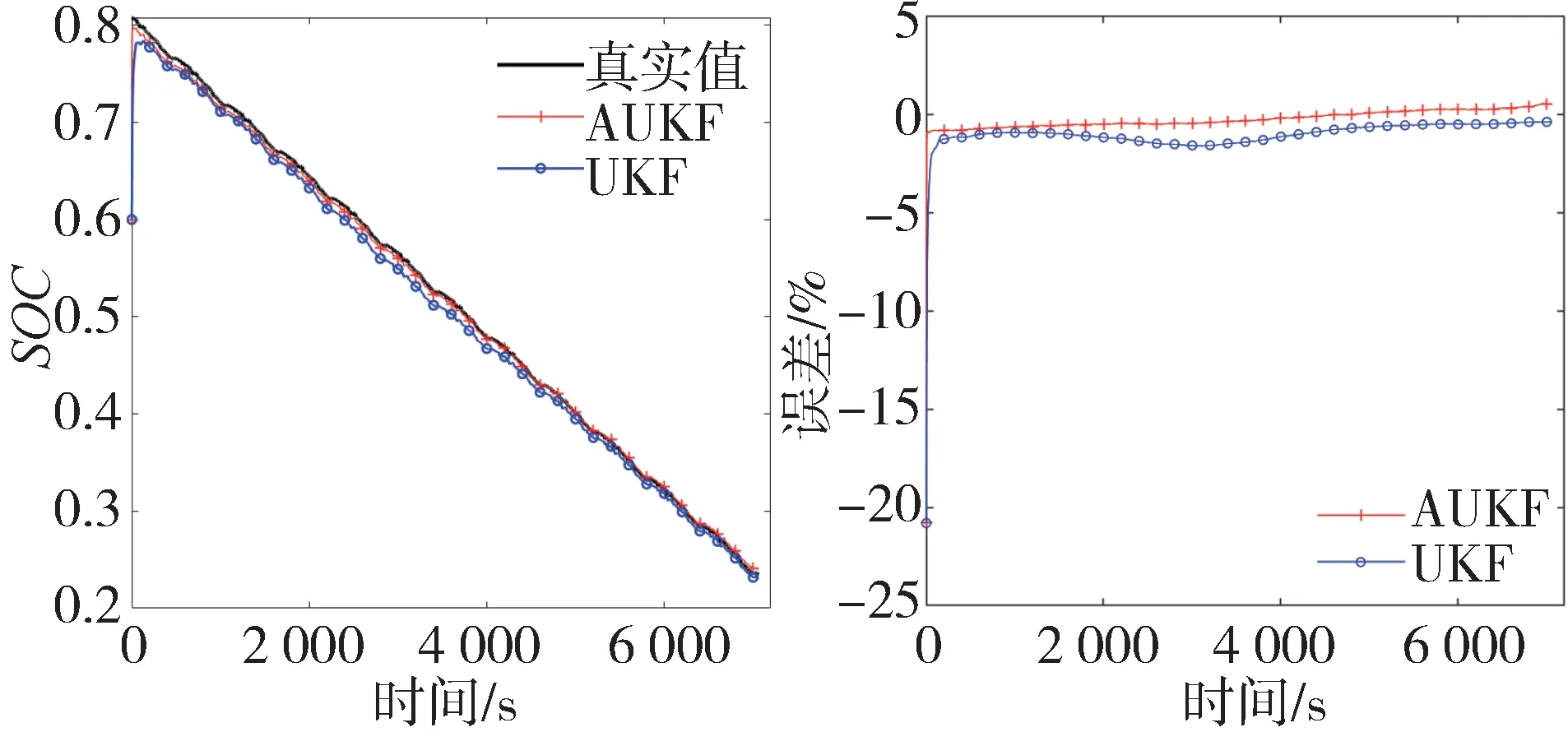
图11 SOC估计结果和误差（US06工况）

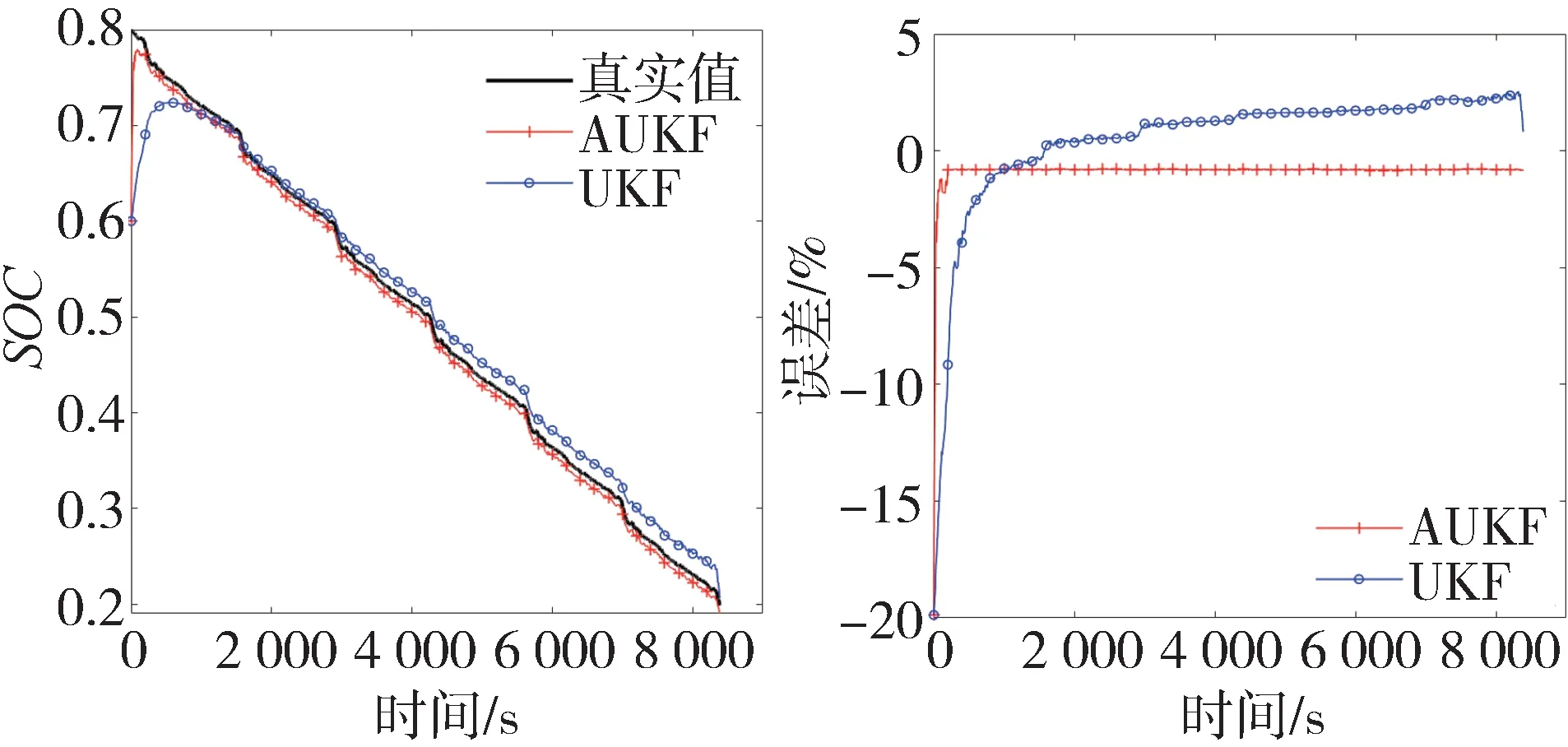
图12 SOC估计结果和误差（FUDS工况）

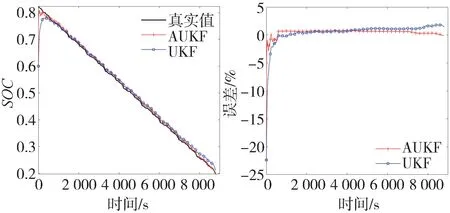
图13 SOC估计结果和误差（BJDST工况）

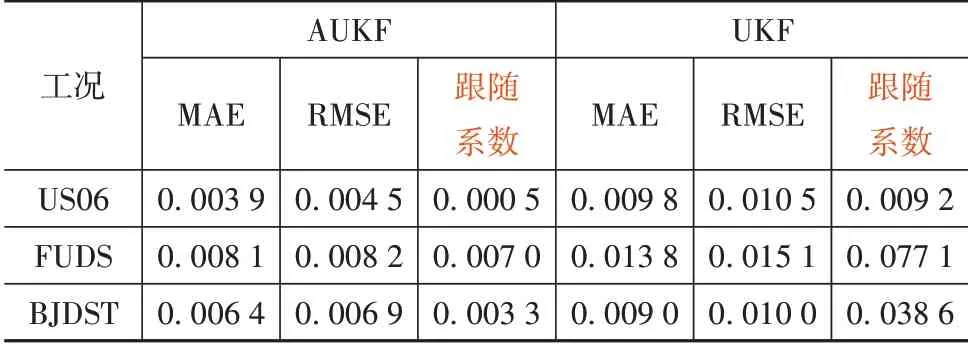
表3 马里兰数据集上的SOC估计误差与跟随系数

5 结论

首先介绍RC等效电路模型及其数学描述，完成了参数辨识和模型建立工作，并提出了一种阻容参数的二维插值方法，对阻容参数随SOC 的变化进行建模。其次针对常规UKF 存在的问题，提出了一种AUKF 算法，该方法将滤波器的一般性收敛判据引入UKF 中，并通过对测量噪声协方差、过程噪声协方差和卡尔曼增益进行自适应调整，提升了滤波算法的稳定性和收敛性，降低了对电路模型精度的依赖。最后在实际测试数据的DST 工况、马里兰大学电池数据集的3 种循环工况中进行实验验证。结果表明在不同的测试工况下，与常规UKF 算法相比，所提出的AUKF 算法皆具有较高的估计精度、较小的跟随系数和较平稳的估计曲线。