基于关键点提取的人体活动识别

郭华峰,向长城，宋礼文，陈世强

(1.湖北民族大学 数学与统计学院，湖北 恩施 445000；2.湖北民族大学 智能科学与工程学院，湖北 恩施 445000；3.湖北民族大学 新材料成型及装备技术产学研中心，湖北 恩施 445000)

随着人体活动研究的不断发展，人体活动识别已经成为医学工程的重点研究领域.人体活动识别作为一种与面部、指纹等识别类似的研究领域，具有固定性强和受环境影响小等特点.其中使用加速度传感器数据，可以在用户的日常行走时进行活动识别，不需要用户过多的配合，提高了用户的满意度.

近年来，许多国内外研究人员使用加速度传感器开展人体活动识别研究，取得了令人振奋的成果.使用可穿戴式传感器数据，基于隐马尔科夫模型(hidden Markov model，HMM)来构建活动识别系统的有监督建模方法已被广泛应用[1-3].目前，基于智能手机传感器的人体识别研究已取得一定的成果[4-7]，且被适时应用到对人体的识别当中去.Trabelsi等[8-9]使用改进的HMM算法，对提取的传感器数据进行活动的识别与分割，其活动识别准确率分别达到了91.4%、90.3%.Akiduki等[10]提出了基于奇异值分解的加速度数据识别算法，对穿戴在人体不同位置(右小腿、左大腿、背部下侧和左前臂)传感器采集的加速度数据进行聚类识别和方差分析.Wang等[11]使用自适应隐马尔科夫模型，基于Cox回归分析的渐近算法进行人体活动识别，在其选用的步态数据集上平均识别准确率达到90.7%.Preece等[12]对采集的人体加速度信号进行识别时采用提取加速度的特征(均值、方差、传感器任意轴的相关系数等)，其分类准确率达到95%.张向刚等[13]针对人体走路时的步态数据，以HMM为基础，利用特征训练对人体活动开展识别，得到了很好的识别效果.刘斌等[14]针对三维加速度传感器信息，使用4种典型的统计学方法建模，分别对不同的人体行为活动(如站立、行走、跑动、坐下等)进行识别.Tao等[15]提出一种基于微机电系统(micro electro mechanical system，MEMS)惯性传感器信息综合判别的人体运动模式识别算法，对站立、跑动、速走、慢走、上楼、下楼6种活动方式开展识别研究.Zhang等[16]对采集加速度数据的特征点稀疏聚类表示步态识别，其准确率达到95.8%.

对上述工作分析后发现，在关于加速度数据进行人体活动识别过程中，长时间跨度的活动方式如走、跑、静坐等日常动作已经达到了非常好的识别率.但要实现快速识别及实时检测，依然存在一些值得关注的问题，如不同活动之间的快速转换识别、模型复杂度过高、动态活动与静态活动混合识别模糊等，这些都是实现人体活动识别必须要处理的重要问题.

针对以上问题，对数据集上的人体活动数据进行关键点(key point)[17]抽样处理.关键点作为时态信号的一种特征，可以用来刻画原始时间序列的全局特征，进而用关键点组成的序列来近似表示原始时间序列.为检验在关键点条件下的有效性，提出混合隐马尔科夫回归模型[18]开展活动识别，该模型将活动识别问题转化为多维时间序列的活动联合分割问题，每段分割都与一个活动相关联，可以实现对活动区域的定位分割.理论分析和实验表明，提出的方法在长时间跨度、采集固定和特定着装的前提下，仍可以实现对人体行为活动的准确识别.

1 关键点描述

由于人体活动的连续性及时间的持续性，传感器数据采集过程中会产生大量的时间序列数据，会导致数据对时间跨度的依赖过大.活动信号关键点提取算法可以降低算法模型的时间复杂度，同时保留三维信号的时域特征，根据相应的关联规则来检测关键点，通过分段检测方法来提取符合规则的关键点.在一段时间序列内，若存在关键点，则在该点两端的时间序列呈现出不同的变化趋势.如图1中时间序列所展示，点A左侧呈现上升趋势，右侧呈现下降趋势，定义为极值点，反之亦然；点B左侧为上升趋势，右侧趋于平缓，定义为转折点，反之亦然.总结这两种方式出现的点集合为关键点集合.

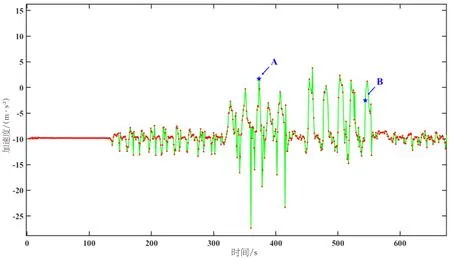
图1 两类不同关键点Fig.1 Two different types of key points

加速度数据序列是三维时间序列，其中每个维度都表现为时间序列信号，因此通过提出的MHMRM模型将活动识别问题表述为时间序列的分割问题.将提取关键点后的数据划分为时间序列后，为更好地对实验结果作出评价，对提取关键点后生成的训练集数据进行活动的标记.

2 算法分析与描述

2.1 模型介绍

(1)

其中zi是一个离散隐状态变量，与某一活动相对应.βzi=(βzi,0,…,βzi,p)T是p维多项式回归模型系数，其中σzi是相应的标准差，εi是一个满足标准高斯分布的附加噪声.

假设MHMRM模型每个时间序列点xi下对应的观测值为xi=(xi1,xi2,…,xim)，由以下回归模型生成:

(2)

xij为时刻i的第j个观察向量.每个时间序列xi来自k个混合集群活动，k对应活动的数量，使用权重(π1,…,πK)来衡量选择每个活动的比例.xi的条件混合概率为

(3)

其中，πk=p(zi=k)满足π1+…πk=1.βk是第k个多项式回归模型的(p+1)阶系数，t是m×(p+1)阶矩阵.

2.2 参数估计

对完全数据[xi,zi]=[(xi1,zi1),…,(xin,zin)]开展参数学习过程，需要对模型参数进行初始化处理.对状态转移矩阵的先验进行初始化如下:πk=p(zi1=k|π,t1),

(4)

满足πk≥0且∑kπk=1，然后对t=2,…,n对应的剩余值根据以下转移概率递归方式生成:

Mlr=p(zi,q=l|zi,q-1=r,M),

(5)

(6)

对收集到的训练集开展参数估计θ=(π,β,M,σ)，使用EM算法解决参数估计问题，这个问题可分为两步.

1) 期望估计.所提出的模型的完整数据概率密度为

p(X,Z;θ)=p(Z;π,M)p(X|Z;θ),

其中X=(x1,…,xn)，Z=(z1,…,zn)，可以得到完全数据的对数似然函数为

(7)

完全数据对数似然函数.其相应期望值:Q(θ,θ(i))=Ε(L(θ)|X,t;θ(i)).

进一步计算可以得到:

(8)

2) 最大化估计.对上述式(7)最大化，对于生成每个参数的更新规则，如下所示.

先验概率πk更新规则:

(9)

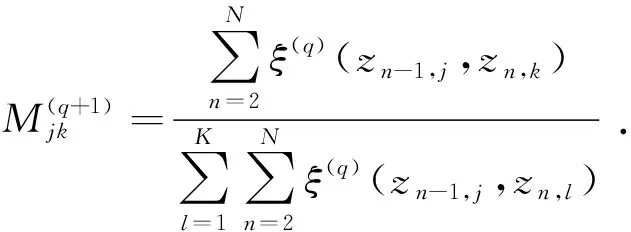
(10)

(11)

(12)

经过EM算法得到参数θ后，使用维特比算法(Viterbi algorithm)来估计相应的状态序列.该算法在给定相应的参数θ以及观察序列X=(x1,x2,…,xn)，寻找最有可能的状态序列Z=(z1,z2,…,zn).

3 实验与分析

3.1 实验数据集分析

设计了不同的混合活动，包括3种静态活动 (坐、躺、站立)和5种动态活动(慢跑、上楼、下楼、步行、跳).这些活动模拟现实生活环境中身体动作.表1给出了参与采样过程的8名受试者的详细信息(每个参与者执行8项活动),图2给出了传感器位置设置示例.

表1 采样人员信息分配Tab.1 Sampling personnel information assignment

图2 手机传感器位置Fig.2 Mobile phone sensor location

样本数据中提取的片段长度并不相同，因为所有活动采集的数据都是不同受试者模仿现实活动.为了使不同活动和主题的维度保持一致，所有训练集不同维度都需要调整为具有相同长度的数据集.因此，对数据进行重采样，以便不同数据集下各维度样本保持一样的长度.

3.2 模拟训练和实验结果分析

算法使用Matlab R2020b来执行算法程序，使用配备Windows 64位系统、Intel Core i7-7700HQ(频率为2.8 GHz)和16 GB内存的PC机.对于人体活动分割，提出算法的性能基于采集过程中活动状态标签相对于真实标签被正确预测的数量来衡量.使用准确率(accuracy)、召回率(recall)、精确率(precision)以分段方式来评估所提方法的性能.

(13)

(14)

(15)

TP为步态项转换持续的时间，预测为步态项转换持续时间；TN为非步态项转换持续时间，预测为非步态项转换持续时间；FP为非步态项转换持续时间，预测为步态项转换持续时间；FN为步态项转换持续时间，预测为非步态项转换持续时间.

针对原始加速度信号的人体活动分割，选取两组数据集验证方法的有效性、可行性.表2描述了两组不同长度的活动采样集合.

表2 采样信息Tab.2 Sampling information

图3给出了两组混合活动的识别分割结果和后验概率，可见算法对不同静态和动态活动分割识别结果符合预期目标.尽管在动态活动和过渡区域之间存在一定的混淆，例如S2和D5之间的过渡区域没有给定相应的划分区域，这是由于在活动转换过程中采集到的活动趋势与不同动态活动呈现的时间序列相似，图3(b)中这种现象最为明显.其次，由于动态活动之间的转换，人体动作幅度过大会导致动作的骤变，从而不出现过渡区域，例如步行和慢跑之间存在活动的骤变，但不影响整体的分割识别效果.

(a) 数据集1算法分割识别结果 (b)数据集2算法分割识别结果图3 活动验证示例Fig.3 Examples of activity verification

表3显示了算法对不同混合活动的识别结果.对比算法在不同混合活动之间的分割识别，两种不同活动之间存在一定长度的过渡区间，过渡时间较长的区域分割会出现一定的混淆，但分割识别结果是有效的.可以看出，MHMRM方法对8种活动的平均准确率均达到了90%以上，对静态活动的分割识别性能尤为理想.观察不同测试集之间的混淆,发生在不同动态活动过渡之间的混淆最为明显,导致这种现象出现的原因是传感器采集数据时动态活动转换中会出现不同程度的抖动,使得观察方向的加速度数值变化较小,从而导致行为活动分割的误差较大.

表3 不同混合活动的评价结果Tab.3 Evaluation results of different mixed activities

为验证算法的分类识别性能,选取传统的机器学习算法及其他性能优异的算法开展对比.文献[8]为一种经典的隐马尔科夫回归(multiple regression hidden Markov model，MRHMM)分割方法，文献[9]是一种利用Logistic过程输出信号的隐过程人体活动识别算法(multiple regression model with a hidden logistic process，MRHLP)。除此之外，分别利用了其他3种标准的分类方法开展活动对比，包括HMM、支持向量机(support vector machine，SVM)、朴素贝叶斯分类器(naive Bayes).如图4所示，给出了6种算法对8种活动的分割识别结果，可见本文算法对静态活动和动态活动的平均准确度都在90%以上，高于其他几种成熟的人体活动识别算法，证明了提出算法拥有较高的实效性.

图4 不同算法准确率对比Fig.4 Comparison of accuracy rates of different algorithms

4 结论

提出了一种便捷、快速的人体活动识别解决方案,用于对不同个体的关键点信号进行活动识别.针对传统的机器学习中时间复杂度高、训练时间长以及分类识别性能不佳等问题,设计了混合隐马尔科夫回归模型.该模型对不同个体的状态信息进行分类,在保证良好的分类识别准确率的前提下大幅降低了模型的复杂度.与其他成熟的机器学习活动识别方法比较,所提出算法在活动识别实时性的前提下,能够分别对静态活动与动态活动进行检测,使得对活动的区分更加细化,进一步提高人体活动识别的效果.在未来工作中可以对算法迭代时的先验分布开展处理,提高人体活动识别的效率.