基于双阶段网络模型的改进多变量广义预测控制
2022-08-03丁海丽陈宽文刘朋远胡婷婷
丁海丽,陈宽文,刘朋远,胡婷婷,梁 飞,杨 杨
(1.国网宁夏电力有限公司营销服务中心(国网宁夏电力有限公司计量中心),银川 750002;2.南京邮电大学 自动化学院、人工智能学院,南京 210023)
0 引言
非线性和时滞特性是工业领域中存在的普遍特性,影响着系统辨识及控制的性能。对存在非线性和时滞特性的系统进行辨识和控制方面的研究具有重要的理论和现实工程意义[1]。
非线性时滞特性的存在增加了控制的难度。部分系统输出往往不能实时地表现出系统的控制效果和所遭受到的扰动,在接收到控制信号后,系统需通过一段时间的延迟后被控量才会受到该具有的控制,此类系统具有的特性被称为时滞特性。时滞特性普遍存在,如声音在空气中的传播,电信号在电子设备中的传递等都具有延迟特性。对实际系统来说,时滞有较多产生的原因,如物质的传输、信号的传递和反应的运行等都需要时间,这些都会导致时滞现象的产生。系统时滞的存在会导致系统的控制难度增大,系统难以在重要的时刻快速控制调节,引起较大超调以及调节时间,造成控制质量的降低。且部分系统时滞还伴随着非线性特性,系统的稳定性能会进一步降低,甚至引起振荡、发散。因此时滞系统因为本身的时滞特性一直以来是工业领域控制的重点难点问题之一[2]。
系统辨识简单来说是对系统数学模型进行确定的理论。学者L.A.Zadeh对“辨识”这一词汇给出定义[21]:辨识是在设定的一类模型里,考虑输入输出参数,建立与观测系统等同的模型。对于现代控制理论而言,主要包括三部分的内容:系统辨识、控制理论以及状态估计。系统进行辨识是现代控制研究的基础。在实际的控制研究中,需要建立模型,从而解决实际的控制问题。因此完成系统辨识工作,确定系统的数学模型就显得特别重要。非线性时滞系统的辨识问题是辨识领域的重要研究方向。
传统的系统辨识方式主要包括基于阶跃或脉冲信号的响应法,最小二乘法、极大似然法、卡尔曼滤波法等。基于阶跃或脉冲信号的辨识方式采用阶跃或脉冲信号作用于被控对象,观测输出响应,完成系统辨识。但在实际的工业生产过程中,较难进行阶跃或者脉冲信号的反应工作,获取相关数据。最小二乘法作为最为常见的系统辨识方法,其算法简单易懂,应用范围较广。但使用最小二乘法估计参数是非一致的,在其基础上衍生出了递推最小二乘法、广义最小二乘法等。值得注意的是最小二乘辨识方法对系统输入数据有着较高的要求,使得最小二乘法在诸多情况下难以应用。极大似然辨识方法具有良好的理论依据,在线性和非线性情况下都可以完成辨识操作,但计算过程复杂,并且获得的辨识模型大概率是局部最小值,无法获得全局辨识能力。传统系统辨识方法日趋完善,为系统辨识带来了较好的效果,但由于其本身大多都存在局限性,难以满足对复杂非线性时滞特性系统的辨识需求。
随着现代智能控制理论的发展,学者们对辨识领域展开了更深入的研究,产生了诸多结合模糊理论[10]、遗传算法、神经网络等方法的智能化辨识方案。基于模糊理论的辨识方法就是将模糊理论应用到辨识领域,模糊理论基于模糊集合的基本思想,利用连续的隶属度函数理论,在宏观思想上,借助人的思维解决常规方式无法处理的模糊问题。采用模糊理论完成辨识,即将系统的输入输出数据设置为各类模糊集合,并创建模糊规则表,根据输入输出值对应模糊集合进行辨识完成模糊模型的获取。遗传算法是在达尔文的自然选择理论等基础上提出了一种智能优化算法。其将自然界事物的进化过程作为最优解的求解过程,使得获取的解具有较强的搜索范围以及全局收敛等特性,将遗传算法用于系统辨识,则模型具有更强的全局最小值。神经网络是近现代出现的一种新型技术,具有非线性映射、自适应学习等能力得到了广泛的应用。采用神经网络完成系统辨识,仅需根据输入参数设计神经网络结构,即可通过神经网络模拟未知系统的运行状况,获取系统输入输出间关系,完成未知系统的辨识,是种优秀、便捷的辨识方法。凭借神经网络不需事先预知被控对象数学模型的情况下亦能够完成对任意非线性系统的逼近这一优良特性,在系统辨识方面有着较大潜力。
除了系统辨识问题,时滞系统的控制也是重要的研究方向。针对非线性时滞系统的控制问题,学者们提出了良多的解决方案,如鲁棒控制[3-4]、自适应控制[5]、预测控制[6-9]、模糊控制[10-11]、专家控制[12]、神经网络控制[13-15]等方案,以求能减少非线性和时滞特性所导致的系统控制精度低下、系统不稳定等问题。但仍存在一定的不足。鲁棒控制是设计一种在系统参数存在部分不确定性或系统模型具有部分未建模的动态特性时,依旧可以保持系统稳定的鲁棒控制器,但其工作状态不是最优状态,其稳态精度差;自适应控制不需要数学建模、鲁棒性强、有很强的容错能力,但是其对于信息简单的模糊处理将导致系统的控制精度降低和动态品质变差,且设计尚缺乏系统性,无法定义控制目标;模糊控制利用了模糊的思想,对于模型的需求较低,因此对时滞系统这一模型建立困难、不确定性的系统能够进行有效的控制,但其的控制精度较低,无法保证精确控制;专家控制方案具有鲁棒性强、维护便捷等优势,但其自学习能力较弱,对“专家”知识的要求更为苛刻,具有一定的局限性。
结合各方案的优势,设计复合方案是现在非线性时滞系统控制问题的重要研究方向之一。将神经网络控制对非线性、强时变、不确定等系统的处理能力融入到预测控制中,使得神经网络预测控制表现出传统预测控制方案所不具有的优良特性。而且为了提高广义预测控制的精度,结合比例积分(PI)思想,采用比例积分结构对广义预测控制的目标函数进行优化设计;同时对广义预测控制的控制增量选取策略进行改进,利用预测的未来时刻控制增量对当前时刻的控制增量进行修正,优化控制效果。
结合前述工作和思路,本文提出基于双阶段网络模型的改进多变量广义预测控制方案。主要包括两个部分:1)提出一种多变量双阶段神经网络时滞预测模型,即将在本文提出的双阶段神经网络时滞预测模型应用到多变量的情况,作为多变量广义预测控制的预测模型;2)提出一种改进PI性能指标型多变量广义预测控制器,即考虑变量之间的耦合关系,将本文的改进PI性能指标型广义预测控制器应用到多变量非线性时滞系统中。
1 多变量双阶段神经网络时滞预测模型
预测控制是一种基于预测模型,由于滚动优化和反馈矫正等单元构成的控制策略,其主要通过利用未来输出预测值完成系统控制,可有效解决系统存在时滞等问题。在控制存在大时滞非线性特性的系统时,首先需要建立系统预测模型,在建立适当的系统预测模型基础上,进一步设计有效的预测控制方案。神经网络具有优秀的自学习、非线性函数拟合等能力,是作为时滞系统预测模型的理想工具,但是神经网络同时存在着隐藏层节点设置困难,局部最小值等问题。为此通过结合快速回归算法和蝙蝠算法设计一种双阶段神经网络时滞模型辨识方法,可有效解决上述问题,建立精确的非线性时滞系统多步预测模型,为非线性时滞系统预测控制方案的设计打下基础。
包含时滞的单输入单输出(SISO,single input single output)非线性系统自回归滑动模型为:
ym(k)=f[y(k-1),...,y(k-ny),
u(k-d),...,u(k-nu)]
(1)
其中:y(k)代表k时刻系统的输出,u(k)代表k时刻系统的输入,ny、nu为模型的时域,f(·)为非线性函数。
同理,若对具有时滞的多输入多输出(MIMO,multiple input multiple output)非线性系统自回归滑动平均模型进行描述,则可将其在一个离散的采样时间k中的第j个模型的输入输出过程表示为:
ymj(k)=fj[yj(k-1),...,yj(k-ny),
u1(k-dj1),...,una(k-djna),
...,u1(k-nu),...,una(k-nu)]
(2)
其中:uj(k)和yj(k)分别为第j个模型在k时刻的输入和输出向量,fj(·)代表第j个模型的一个非线性函数,dji为第i个控制信号在第j个模型中存在的系统纯时延,ny和nu为系统阶次,j=1,2,...,nb,nb、na为多变量系统中输出、输入变量的数量。
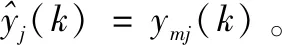
同时可以计算k时刻第j个模型一步的超前预测为:
...,una(k-djna+1),...,u1(k-nu+1),
...,una(k-nu+1)]
(3)
递推可得第j个模型n步的超前预测为:
u1(k+n-dj1),...,una(k+n-djna),
...,u1(k+n-nu),...,una(k+n-nu)]
(4)
此时便可依靠预测模型前几步的预测输出值和控制信号,得到下一步的预测输出值,最终实现对于多变量系统输出值的多步预测。
注1:传统广义预测控制通常使用线性受控自回归滑动平均模型作为预测模型,但面对强非线性系统时,此模型不再适用,因此将设计的双阶段神经网络时滞模型替换传统预测模型应用到广义预测控制中。通过多步预测的策略实现对非线性时滞系统未来输出值的预测,即收集系统过去、现在和未来的系统控制输入与输出得到k时刻前n步的预测值,并根据输出误差对双阶段网络时滞模型实时优化,从而保证对非线性时滞系统的控制性能。
超前n的多变量双阶段神经网络时滞预测模型的结构如图1所示。预测模型由神经网络输入层、隐层、输出层组成。神经网络采用关于中心点对称的局部分布的非线性函数作为隐层的“基”。因此只要确定神经网络的中心,就可以完成输入矢量到隐层的映射,最后通过对权值的调整实现对任意精度的非线性系统的逼近。
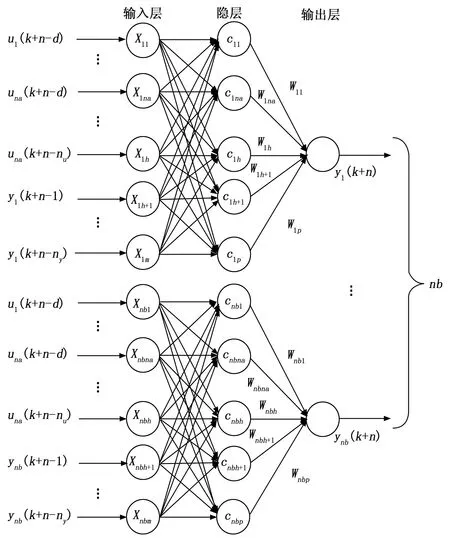
图1 超前n步的多变量双阶段神经网络时滞预测模型
超前n步的第j个双阶段神经网络模型的输入:
Xj(k)=[xj1(k),xj2(k),...,xjm(k)]T=
u1(k+n-dj1),...,una(k+n-djna),
...,u1(k+n-nu),...,una(k+n-nu)]T
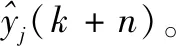
第j个预测模型超前n步的预测输出值:
ymj(k+n) =WjTRj(k) =
(5)
其中:Wj=[ωj1,ωj1p2,...,ωjp]T、Rj(k)=[Rj1(k),Rj2(k),...,Rjp(k)]分别表示第j个双阶段网络预测模型的权值和隐层的输出值。
2 预测控制器的设计
广义预测控制是由Clarke提出的一种预测控制方法[22]。其在预测控制中的预测模型、滚动优化和反馈校正的基础上,创新性的引入了不相等的预测和控制范围,在时滞系统的控制方面表现出优异的控制性能和更强的鲁棒性。广义预测控制通常采用传统受控自回归滑动平均模型作为预测模型,利用丢番方程获取超前的预测输出。由于传统广义预测控制需要解算丢番方程,具有较大的计算量,导致传统广义预测算法运行时间长,实用性能低。为此本文提出改进PI性能指标型多变量广义预测控制器。
2.1 改进PI性能指标型多变量广义预测控制器
对多变量的广义预测控制,其传统受控自回归滑动平均模型的结构可表示[1]:
(6)
式(6)中,d(k)代表在k时刻存在的控制延时;ynb(k)表示在k时刻第nb个系统输出值;unb(k)表示在k时刻第na个系统输入值;e(k)表示系统存在的噪声信号;A(q-1)、B(q-1)和C(q-1)分别为q-1的多项式。
对式(6)进行拆分,根据输入输出关系可将其分解为nb个子系统:
A1(q-1)y1(k)=
q-d1(k)[B11(q-1)u1(k)+…+B1na(q-1)una(k)]+
C1(q-1)e1(k)/Δ
⋮
Anb(q-1)ynb(k)=
q-dnb(k)[Bnb1(q-1)u1(k)+…+Bnbna(q-1)una(k)]+
Cnb(q-1)enb(k)/Δ
(7)
利用单变量广义预测控制的计算方式,对单独的每一个系统进行计算,可得第i个系统超前j步的预测值(忽略噪声影响):
q-di(k)[EijBi1Δu1(k+j-1)+...+EijBinaΔuna(k+j-1)]+
Fijyi(k)=
q-di(k)[Gij1Δu1(k+j-1)+...+GijnaΔuna(k+j-1)]+
Fijyi(k)
(8)
利用式(7)获取多变量系统中第i个系统的n个并列控制器:
gina0Δuna(k-dina)+fi(k+1)
gina1Δuna(k-dina)+
gina0Δuna(k-dina+1)+fi(k+2)…
gi10Δu1(k-di1+n-1)+…+
ginan-1Δuna(k-dina)+…
gina0Δuna(k-dina+n-1)+fi(k+n)
(9)
查看式(8)中第n个控制器,可重新改写为(忽视噪声):
(10)
其中:
ηi(k)=[gi1n-1,...,gi10,...,ginan-1,...,gina0,fi(k+n)]
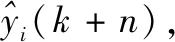
Ri(k)=
(11)
此时ηi(k)的值便可以获得,即可获得矩阵Gi,以及相关矩矩阵Gi1,Gi2,...,Gina,其中:
此时广义预测控制的第i个系统的预测向量fi可通过多变量双阶段神经网络时滞预测模型通过多步超前预测获得,其表示为:
(12)
yi(k)为第i个系统的实际输出,ei(k)=yi(k)-ymi(k)为k时刻的预测误差,为了方便计算一般将h取为1。
同时为了保证系统的控制优化过程更加平稳,第i个系统的参考轨迹设置为:
wri(k+j)=αjyi(k)+(1-αj)yri(k),j=1,2,...,N
(13)
其中:α表示柔化系数。
多变量广义预测控制的最优控制律计算时,需要对多变量之间的耦合效应进行考虑。采用前馈解耦的策略解决多变量之间的耦合问题,将目标函数去中心化,将多变量的性能指标转化为nb个子系统的性能指标进行计算,完成对多变量系统的最优控制律的计算[16]:
Jm(k)=J1(k)+J2(k)+...+Jnb(k)
(14)
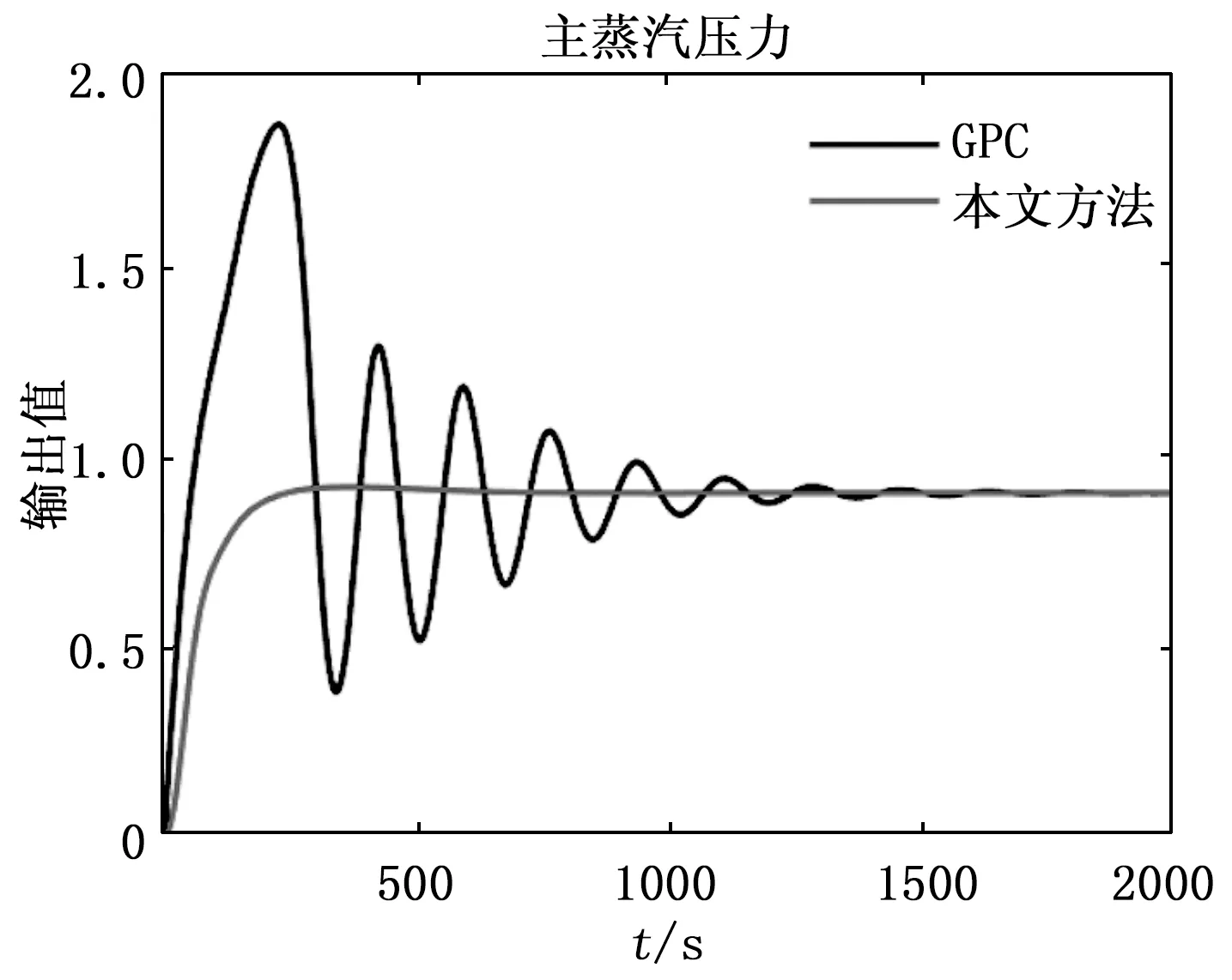
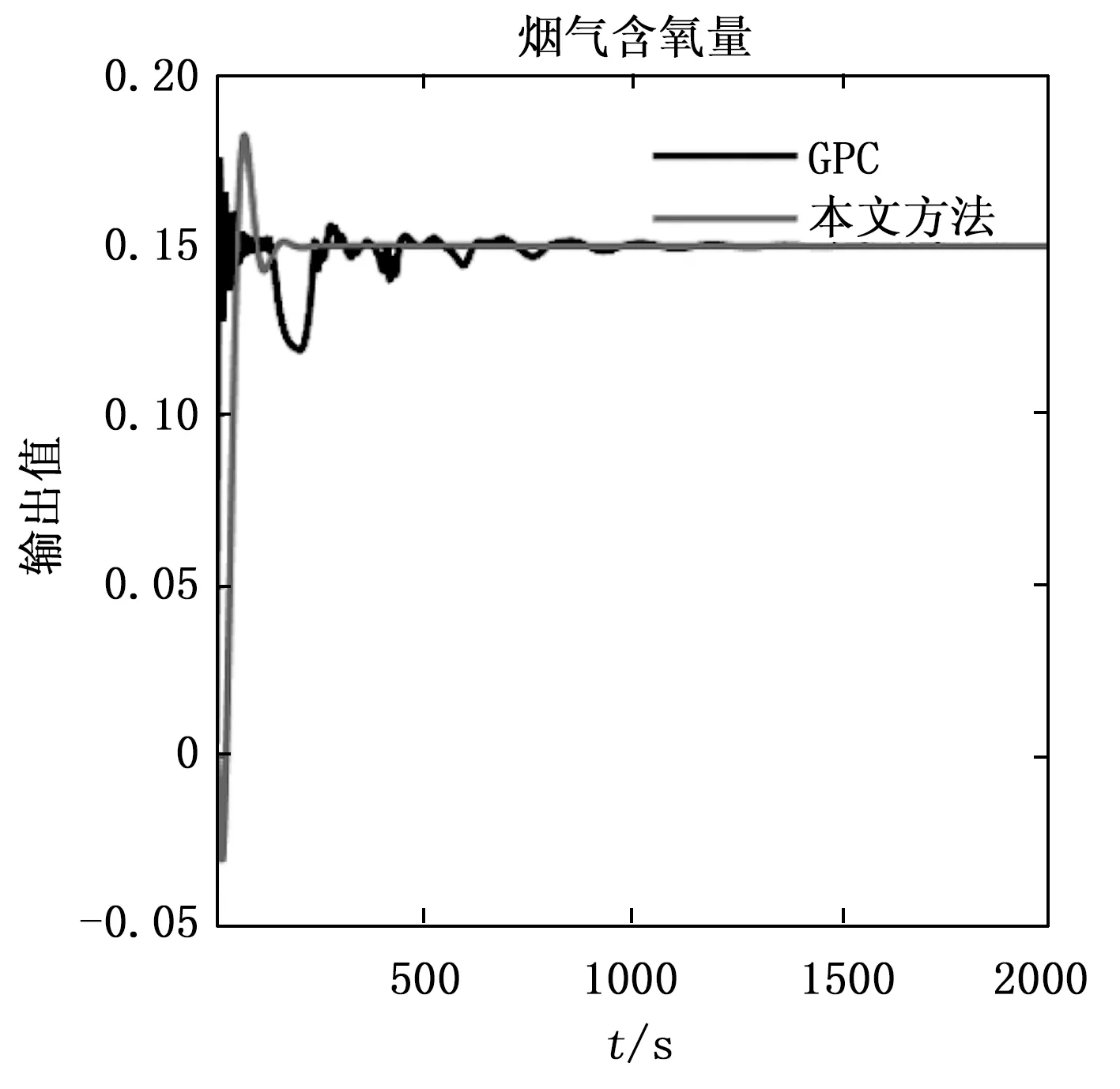
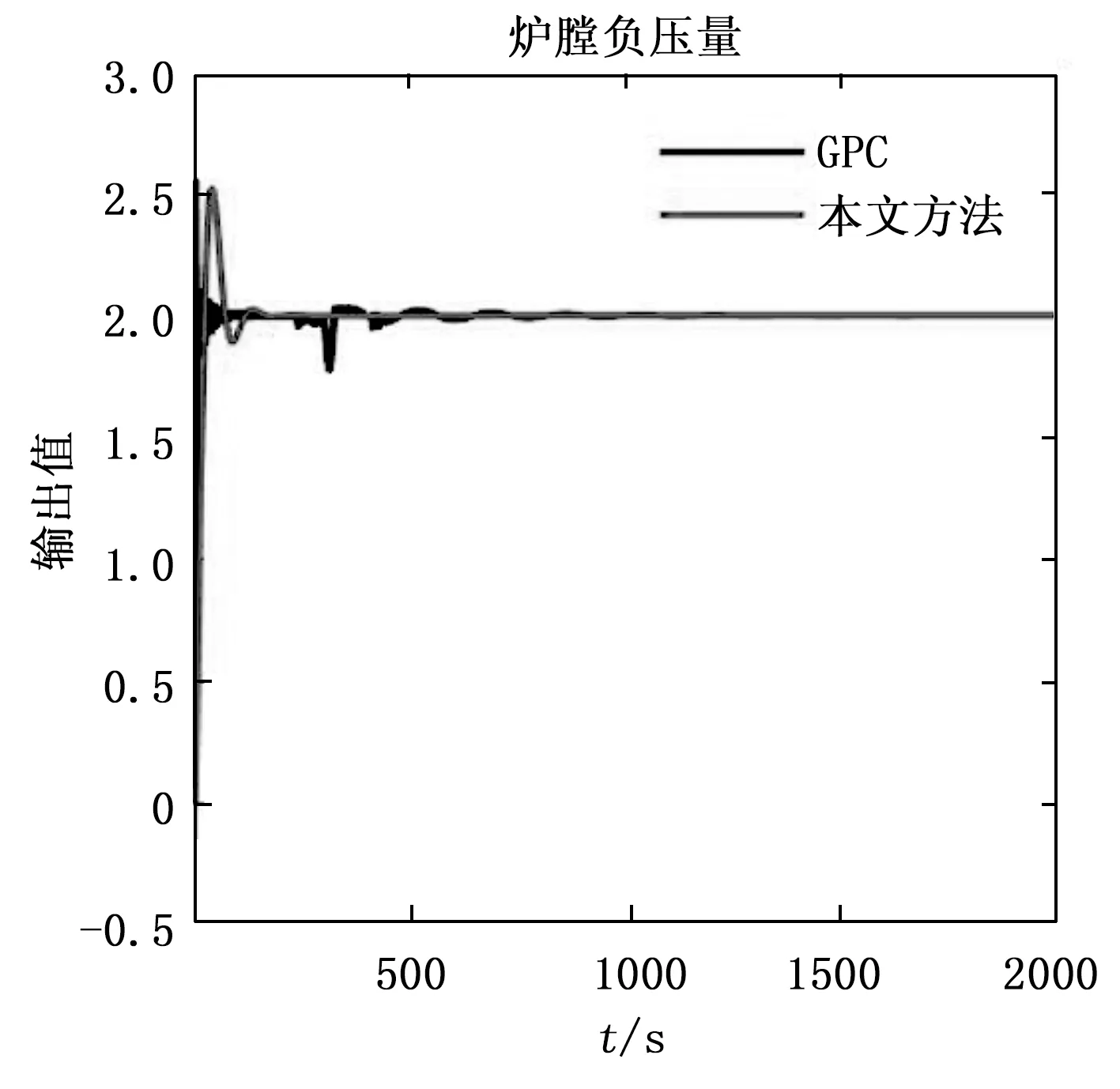
第i个子系统的性能指标为(0 (15) 式中,kp(kp≥0)和ki(ki≥0)分别为比例因子和积分因子,ei(k+j)=yi(k+j)-wri(k+j)与Δei(k+j)=ei(k+j)-ei(k+j-1)。 注2:通过在广义预测控制原单一性能指标中增加比例和积分项,可使控制器在下一时刻的最优控制量选取时考虑过去和现在时刻偏差的影响,进一步改进广义预测控制的控制速率和精度。 利用式(10),可得第i个系统的预测输出为: (16) 通过式(15)、式(16)可得第i个系统的改进PI性能指标型隐式广义预测控制算法的最优控制增量为: ΔUi(k) = (kiGiiiTGiii+kpGiipTGiip+σI)-1 (17) 式中, 通过Rip= (kiGiiiTGiii+kpGiipTGiip+σI)-1kpGiipT和Rii= (kiGiiiTGiii+kpGiipTGiip+σI)-1kiGiiiT,式(17)简化为: ΔUi(k)=RipΔEi(k)+RiiEi(k) (18) 式(17)可重新改写为: ΔUi(k) =(kiGiiiTGiii+kpGiiiTSTSGiii+σI)-1 (19) 令ξ=kpSTS+kiI,此时第i个系统的最优控制增量为: (20) 此时计算出的未来一段时间内最优控制增量,考虑了广义预测控制算法下一时刻的控制增量选取策略,仅有第一个的控制增量Δui(k)被使用计算下一时刻控制量,而其它m-1个计算出的控制增量没有被使用。 本文利用未来预测的控制增量进行优化,结合具有未来变化趋势的未来多时刻预测控制增量修正目前时刻获取的控制增量,完成未来对现在的补偿,从而有第i个系统获得更优的输入控制增量: (21) 式中,β表示修正系数,0<β<0.5。 可得第i个系统优化过的系统控制量为: (22) 注3:传统广义预测控制利用系统预测的未来偏差计算控制量,并未考虑过去时刻的系统偏差。由于预测误差和被控对象惯性等因素的影响,所得到的实际输出很难达到理想的参考值。由于每一步控制都会累计偏差,进而导致系统达到稳定状态的速率变慢[17]。但若考虑过去偏差的影响,广义预测控制的速率将会得到改善。因此本文将广义预测控制和PI思想结合,利用比例积分环节通过历史和当前的误差调节广义预测控制,并优化了广义预测控制的控制增量选取策略。 基于双阶段网络模型的改进多变量广义预测控制结构图如图2所示。预测控制结构主要分为3个部分:预测模型、滚动优化、反馈矫正。预测模型为预测控制提供系统输入输出间对应关系,获取系统未来一段时间的动态变化情况;依靠预测模型获取的系统条件和性能指标函数,滚动优化采用实时的迭代策略得到系统的最优控制律;最后反馈矫正环节利用当前输出和预测输出的误差修正预测未来动态变化的输出值,使得系统输出能够更准确地跟踪参考轨迹或者达到期望状态。 图2 改进多变量广义预测控制结构图 该结构与单变量广义预测控制结构相似,在多变量的情况下采用双阶段神经网络时滞模型作为预测模型,通过多步预测的策略预测每个子系统在未来多个时间段内的输出情况,并依靠输出差值对多变量双阶段网络时滞预测模型进行实时调整。控制器为设计的改进PI性能指标型多变量隐式广义预测控制器。采集每个子系统的参考轨迹、控制信号和模型的预测输出,通过PI性能指标型广义预测控制算法计算出未来多个时刻内的控制增量,后利用改进的控制增量优化策略,得到下一时刻最优的控制输入信号输入给系统,以滚动的方式实现对非线性时滞系统的预测控制[18]。 基于双阶段网络模型的改进PI性能指标型多变量广义预测控制流程如下。 Step 1:输入初始数据并设置神经网络参数和控制器中参数,如预测长度N,控制步长M,遗忘因子λ和柔化系数α等参数; Step 3:获取nb个系统的控制器参数Gij,即由递推最小二乘法(11)实时估计; Step 5:确定目标函数中kp和ki参数,用式(20)计算出每个子系统在PI环节下的GPC最优控制增量ΔUi; Step 7:返回Step 2(k=k+1)继续循环。 为了验证本文设计的控制方案有效性,我们采用300 MW单元机W型火焰直吹式燃煤锅炉系统仿真研究,其具有典型的多输入多输出、非线性和时滞特性。该燃煤锅炉为一个三输入、三输出的复杂耦合系统,输入量为送煤量、送风量以及引风量;输出量为主蒸汽压力、烟气含氧量以及炉膛负压量。保证其在输出量稳定的情况下运行,数学模型为[2]: (23) 构造多变量双阶段神经网络时滞预测模型:设置3个神经网络的输入层数分别为8、10、8,输出层数为1。其中训练集和测试集参数均由燃煤锅炉系统产生,第一阶段训练集数据500组,测试集数据200组,通过快速回归算法建立初始网络模型结构,隐层节点数分别为30、27、28。第二阶段训练集数据2 000组,测试集数据1 500组。其中设置BA算法种群数为40,迭代次数为50;动量梯度下降法学习率为0.05,动量为0.85. 改进多变量广义预测控制器设置预测长度为12,控制长度为4,权值系数为0.85,遗忘因子为0.995,软化系数为0.33。本文方法设置修正系数β为0.4,kp为0.1,ki为0.1,采样时间5 s,设置各输出值的参考轨迹:主蒸汽压力为0.9、烟气含氧量为0.15、炉膛负压量为2,图3~5为控制输出情况。图3为锅炉系统主蒸汽压力输出变化曲线,可以观察到在本文控制方法下系统输出压力经过大约250 s到达稳定状态,而传统广义预测控制方法出现了明显的振荡现象,需要1 500 s左右才进入稳定状态。图4和图5分别为烟气含氧量和炉膛负压量变化变化曲线。从上述实验结果图可知,采用本文方法设计的控制方案,保证了主要的输出值主蒸汽压力的稳定,与广义预测控制[19]相比,其超调量明显降低,振荡趋势明显缓解,并以更快的速度达到了稳定状态。而次要输出值烟气含氧量和炉膛负压量也能以更快的速度达到稳定状态,且输出曲线更加柔和。通过仿真验证了在多变量非线性时滞系统的情况下,本文设计的控制方案具有更强的控制性能,保证了系统的稳定[20]。 图3 主蒸汽压力变化 图4 烟气含氧量变化 图5 炉膛负压量变化 在单变量非线性时滞系统的广义预测控制的基础上,本文设计了一种在多变量基础上的改进广义预测控制方案。方案在考虑多变量间复杂的耦合情况的基础上,将多输入多输出系统转化为多个多输入单输出系统,并设计多变量双阶段神经网络时滞预测模型;采用前馈解耦的方式完成了改进广义预测控制器的设计。通过对300 MW单元机W型火焰直吹式燃煤锅炉系统的仿真研究,验证了改进多变量广义预测控制方案具有更优的控制性能。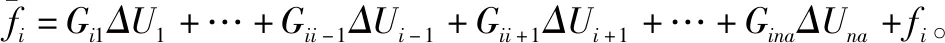
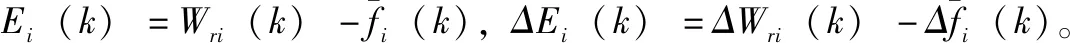
2.2 改进多变量广义预测控制结构
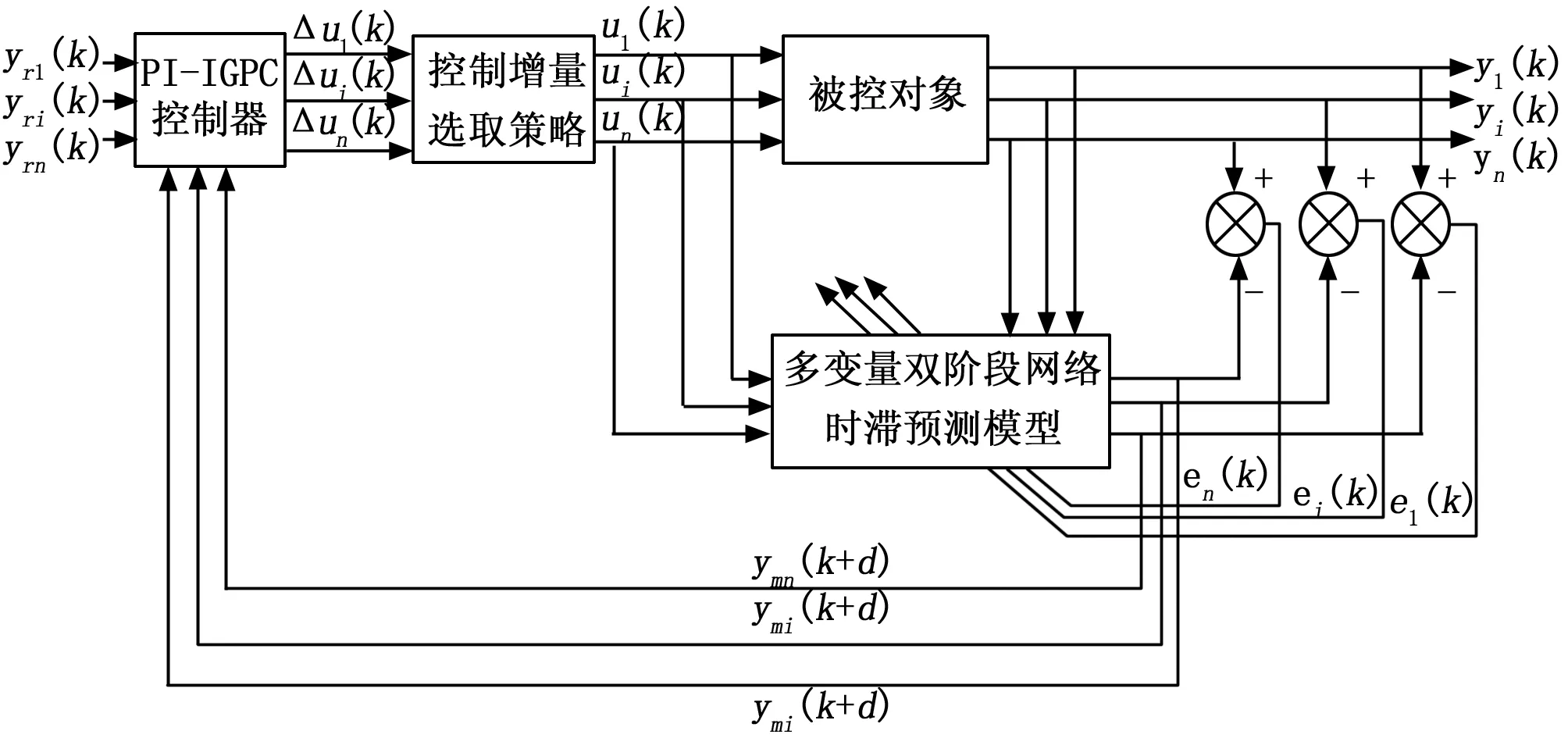
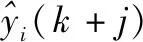
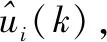
3 仿真实例
4 结束语
