圆锥曲线解题策略探究

张丽燕

（曲靖市第二中学，云南 曲靖 655000）

0 引言

一直以来，在高考题目详解当中，针对圆锥曲线问题的探讨都是重点内容。一般来说，在题目中设置圆锥曲线问题的主要目标就是考察学生在逻辑思维方面的能力，除此之外，针对于运算能力以及空间想象能力也会进行考察，所以圆锥曲线其实是一种综合性的考察方式。

1 教育教学理论基础

在学习圆锥曲线相关问题时，也可以从众多题目当中选择经典题目并找出题目的类别，然后针对这些题目进行总结，分析好具体的策略，这样更加有利于帮助学生进行复习以及掌握知识。

2 高中数学教学当中的圆锥曲线解题策略

对于高中数学教学来说，往年的高考真题就是复习以及学习的珍贵资料，所以这些题型进行研究以及分析就显得非常的重要。在经过针对于五年的新课标真题的分析以及归纳之后，笔者选择将高考圆锥曲线的综合题目分类为以下几种，并且针对每一个题型都进行了简单的阐述，对其解题策略进行相关的探讨，希望能够为学生圆锥曲线问题的学习提供一定的帮助[1]。

2.1 求动点的轨迹方程

在针对动点轨迹方程题目的求解进行研究的时候，不难发现这种题目的一个非常大的特点就在于整个题目的设置非常的灵活。因此在进行方程求解的时候，一定要伴随着条件变化而产生一定的变化，而且在题目进行分析时，使用的方法也非常的多样，其实究其根本，动点的轨迹方程进行研究指的就是求出横坐标以及纵坐标所满足的关系，一般来说，常用的方法包括以下5 点。

2.1.1 直接法

如果动点所需要满足的条件比较简单而且容易表示，那么只需要把条件翻译成数学表达式即可，然后再经过非常简单的代数化解，我们就能够获得轨迹方程。因为这样的方法并不需要额外的一些技巧以及复杂的步骤，为此可以将其称之为直接法。在利用直接法求轨迹方程时，其步骤主要包括四点，分别是建系、设点、列式、化简。

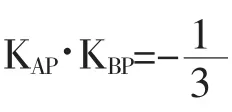
解题：在已经给出的条件当中可以发现，点B 和点A 关于原点o 对称的，因此点B 的坐标是（1，-1）。

2.1.2 定义法

如果我们在阅读题目的时候发现动点的轨迹是题目已经给出来的，并且其轨迹是符合我们已经知道的曲线定义，例如在圆锥曲线学习的过程当中，就发现其包含了四种曲线，这样我们就可以根据已知的曲线定义来把动点的方程求出来，最后只要根据不同的题目做出相应的调整即可。

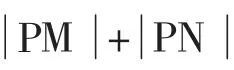
2.1.3 几何法

在平面几何当中比较常见的性质包括角平分线以及线段的垂直平分线等，都是在日常题目当中容易考到的知识点，一般来说，如果在进行动点求解时，该动点符合我们学习过程当中的某一种几何性质或者是某几种几何性质的时候，都会使用几何法来对其进行求解，这种方法和定义法一般会组合在一起使用。针对于题目进行解读的关键就在于必须要从所给的图当中找出垂直平分线以及角平分线具体起到的作用，有的时候也需要根据圆锥曲线的定义来针对于题目进行分析。

解题：如图所示，连接OD。

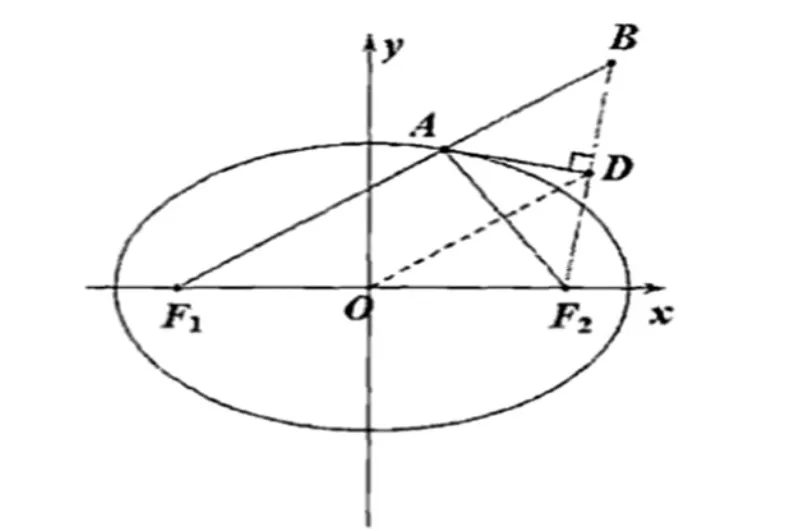
所以点D 的轨迹是以O 作为圆心，2 为半径的圆，也就是说点D 的轨迹方程是x2+y2=4（y≠0），同理，点B的轨迹方程也是以为圆心，4 为半径的圆，因此点B 的轨迹方程是（x+1）2+y2=16（y≠0）。

2.1.4 相关点法

在针对于某些题目进行研究的时候，发现动点p和另外的一个动点m 属于紧密连接的，而具体轨迹方程是题目当中所给出来的一个已知的条件，那么只要建立出m 和p 之间的有效联系，便能够得出动点坐标之间的关系，最终便可以通过代入曲线方程的办法得出x 和y 之间的联系。

2.1.5 参数法

在某些比较特殊的情况下，使用前面几种办法都无法解出题目的具体所求轨迹，发现所求的动点会受到其他因素的影响，例如比值或者是角度等，在这个时候所求的动点坐标当中的横坐标以及纵坐标都和其他的量产生了联系，同时也会随着变量出现变化，将这个变量称为参数，这种方法也可以称之为参数法。

在进行题目求解的时候，如果需要使用参数法的话，那么在得到x，y 和参数之间的联系之后，只需要将题目给出来的这个参数进行消除，就能够得到最终所需要的答案。需要注意的是，所选取题目当中的这个参数具体取值一定要做好相应的描述，因为这样才能够确定好x，y 的取值范围。

2.2 直线和圆锥曲线的位置关系

直线与圆锥曲线位置关系进行考核的时候，其考点在于明晰直线和圆锥曲线之间的位置联系，可以熟练的使用函数以及数形结合，包括等价转换等数学思维来解决问题，从内容上面来看，这也是高考在考察过程当中的重点内容，涉及了直线和圆锥曲线关系当中的弦长面积以及弦中点等一系列的问题。

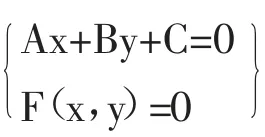
当a=0 时，就可以通过题目演算出一元一次方程，在这个时候其关系为相交关系，并且只存在着一个交点。

当a≠0 时，可以根据具体的数据来对其进行推算，判断出究竟有多少个直线和曲线之间的交点。

2.3 中点弦问题

涉及中点弦的问题都包含着三种类型：①直接把中点弦所在直线的方程具体的数值求解出来，②针对于中点弦的轨迹方程进行研究，③对称问题。通常我们会选取最为简单的方法来进行研究，那就是点差法。首先需要把坐标设置出来，然后根据曲线问题结合有效的公式，寻找出坐标跟弦之间存在着的关系，具体的过程如下所示。

3 结语

综上所述，解析几何是高中教学中一个重点的内容，同样也是高考的重点和难点，而圆锥曲线作为解析几何的一个核心内容，也是新课标要求的五个基本能力的综合性考察，所以是非常重要的。