RPC组合球铰设计与制造安装控制研究
2022-08-02陈经伟
陈经伟
(中铁上海设计院集团有限公司 上海 200070)
1 项目背景
呼和浩特市某市政快速路跨越京包铁路桥梁为(70+70)m T型刚构(见图1),桥梁先顺铁路支架现浇、后水平转体施工跨越铁路到达设计位置。设计荷载为1.3×城A荷载,分两幅布置,半幅桥宽20 m。由于邻近铁路营业线施工,为控制桥梁跨度,需尽量缩小转体承台的尺寸。经综合比选,桥梁转体球铰采用了RPC组合球铰,设计转体吨位为10 000 t。目前,国内外关于RPC组合球铰研究较少,本文主要研究球铰的设计、制造和安装控制。

图1 桥梁现场照片
2 RPC球铰结构设计
RPC混凝土即活性粉末混凝土(Reactive powder concrete),它是以细砂为骨料,掺入大量硅灰等矿物掺合料、高效减水剂和微细钢纤维,薄弱的界面得到大幅度加强,抗裂能提高两个数量级以上,使其成为一种高强度、高韧性、低孔隙率的混凝土材料[1]。
2.1 RPC球铰构造
RPC球铰结构一般由四部分组成,自上而下分别为:球铰上座板、球铰上盘、球铰下盘和球铰下座板,球铰上盘和球铰下盘之间设置超高分子量聚乙烯板滑板的摩擦副,球铰中心设置有中心转轴。球铰各部件结构一般均由钢板焊接而成的钢壳内填充超高强混凝土而组成。
为便于施工操作,球铰上下转盘间隙高度一般可按照0.8~1.2 m设计。下座板埋置于下承台顶面位置,上座板顶面可与转体上盘混凝土底面结合为一体,亦可采用将上座板埋入转体上盘混凝土中的方式。
球铰下盘为具有凹球面的圆柱体,凹球面及外侧面为Q235钢板焊接形成的钢壳,钢壳内填充C120级的超高强混凝土。为保证混凝土与钢壳的整体性和有效传力,内部布置与钢壳内壁焊接的加劲肋板和普通钢筋。球铰上盘为具有凸球面的圆柱体,采用钢壳内焊接肋板并布置普通钢筋后内部填充超高强混凝土的构造形式。
2.2 RPC球铰应力计算方法
如图2所示,可得球冠面积S和投影平面面积S1[2],取K=S/S1,即K=2(1-sinθ)/cosθ/cosθ

图2 球冠面积计算
根据参数分析,K与θ角度的关系如图3所示,K与r、H值的关系如图4所示。
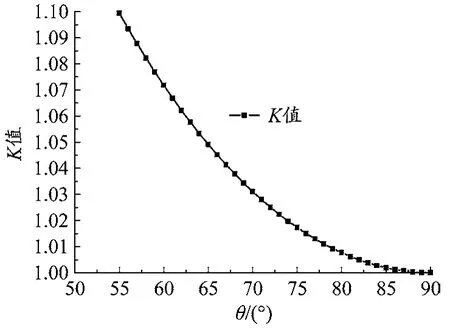
图3 K值与角度关系

图4 K值与r、H值关系
通过分析可知:
(1)K值基本在1.0~1.1之间分布,球铰平面半径越小K值越大。
(2)当球铰平面半径r一定时,随着球冠高度H越高,K值越大。
(3)由于K值变化不大,球铰平面应力计算可近似采用投影面积,与一般平铰计算方式相同[3]。
2.3 RPC球铰设计
本项目球铰采用RPC球铰,如图5所示,球铰由上盘、下盘、上座板、下座板及中心转轴等部件构成。球铰下座板采用角钢支架支撑调平后,与下承台混凝土浇筑为一体。吊装球铰下盘、上盘及下座板,插入球铰中心转轴,将球铰下盘和下座板、球铰上盘和上座板用钢板焊接固定。立模浇筑球铰上盘,将上座板锚固于上盘混凝土内。球铰下盘球面板上铺满8 mm超高分子聚乙烯滑板,采用沉头螺钉固定于球面板上[4-5]。
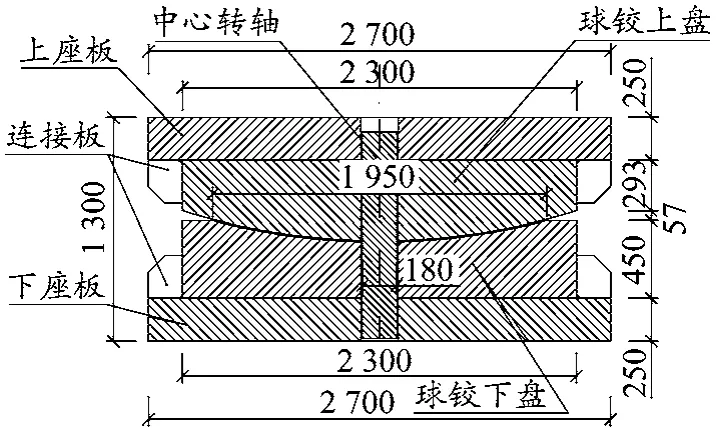
图5 RPC球铰构造(单位:mm)
按照球铰应力计算方法及球铰构造,球铰设计应力可按照下式进行计算[6-9]。
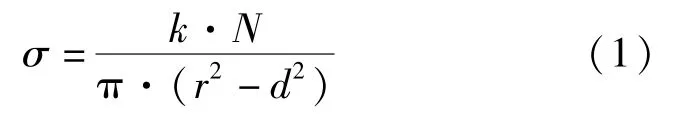
式中,N为球铰设计荷载,本项目N=10 000 t;k为荷载增大系数,本项目k=1.2;r为球铰球面投影半径,取r=0.975 m;d为球铰中心转轴半径,取d=0.05 m。
经计算球铰设计应力为40.6 MPa。C120混凝土设计允许应力42 MPa,强度满足要求。
同理,可计算得球铰上座板应力20.96 MPa。因此,球铰上、下承台采用C40混凝土。
3 RPC球铰误差对球铰应力的影响
3.1 RPC球面半径误差对球铰应力的影响
根据前面研究结论,可知球铰承压面应力可近似采用平铰的应力计算方法。
因此,球铰承压面平均压应力:

C120混凝土设计强度42 MPa,本项目按照40 MPa取值,分析不同球面半径误差对球铰应力的影响,如图6所示。
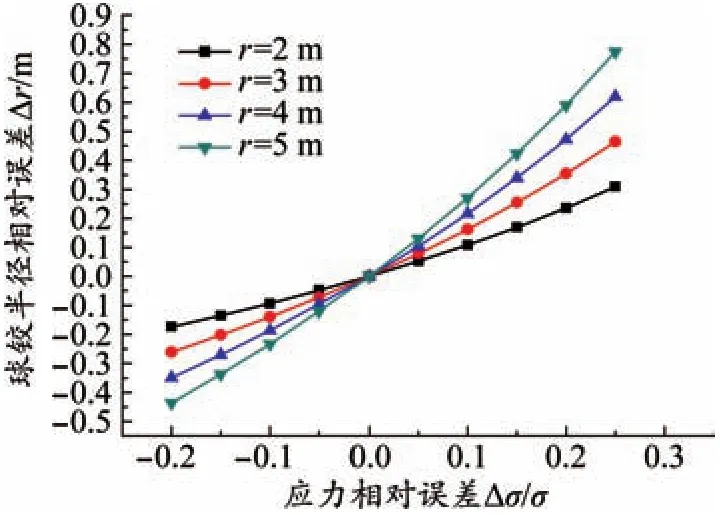
图6 球面半径相对误差和球铰应力相对误差关系
由此可见,球铰半径误差与球铰应力成正比关系。球铰可按Δσ/σ≤5%的控制条件,对球面半径进行误差控制[10-12]。根据RPC球铰构造特点,球铰半径误差宜控制在8 cm以内。
3.2 RPC球面局部误差对球铰应力的影响
当球铰承压面平均压应力为σ时,滑块的平均压缩变形量为:
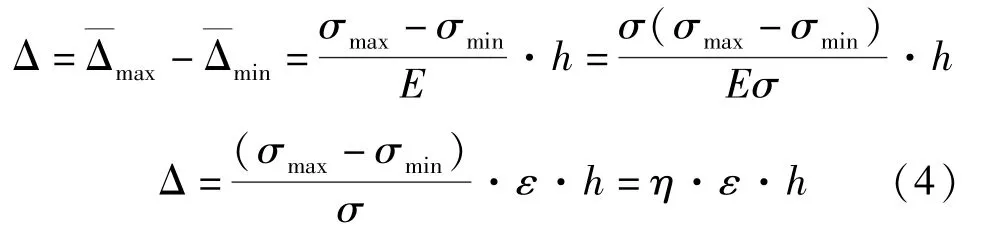
球面摩擦副滑块采用h=8 mm厚的超高分子量聚乙烯板,滑板弹性模量一般为500~900 MPa,考虑蠕变影响后可采用换算弹性模量300 MPa。当平均压应力σ=40 MPa时,球面局部误差Δ与球面应力偏差相对值η及球面摩擦副滑块厚度h正相关,如图7所示。

图7 球面局部误差与球面应力偏差关系
4 RPC球铰安装控制
4.1 上下球铰间隙控制
球铰除了在承受竖向荷载时能够实现水平转动之外,还应当能够适应少量竖向转动,且球铰上下转盘安装时,也存在一定的间隙。桥梁转体到位后,进行最后的空间姿态调整时,也需要少量的竖向转动。
如图8所示:
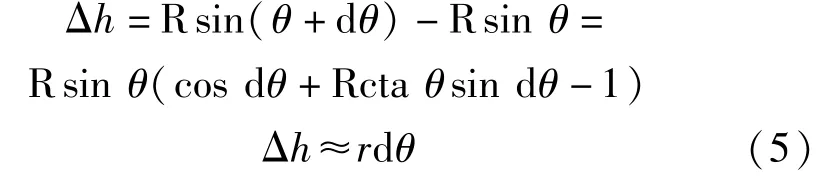
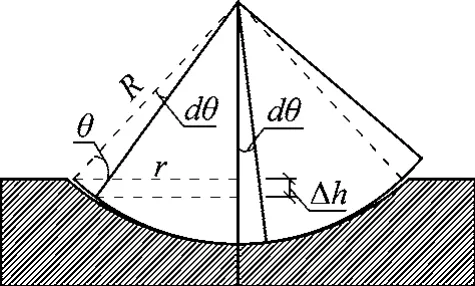
图8 球面竖转位移示意
式中,Δh为上下球铰间隙;r为球铰球面投影半径,取0.975 m;dθ为球铰容许转角,取0.02。
RPC球铰的竖向转角可参照球形支座的容许转角0.02弧度控制[13]。根据上述公式可得,上下球铰间隙可按2 cm控制。
4.2 滑道安装精度控制
理论上转体过程中撑脚不受力,仅靠球铰自身摩阻力平衡上部不平衡重量。而实际操作中,可适当保留部分偏载,便于控制转动中的平衡状态。球铰上转盘可根据大小布置8~12组撑脚,如图9所示,用于转体过程中支撑上部偏载。理想状态时,一半撑脚受力。非理想状态时,单个撑脚受力。
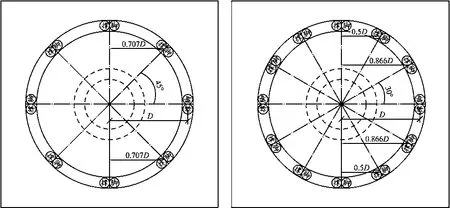
图9 球铰撑脚平面布置
当滑道局部平面安装误差较大时,可引起局部撑脚脱空,从而导致其他位置撑脚受力增加;当滑道整体安装误差较大时,可造成仅仅一组撑脚受力。
当采用8组支撑,局部一组撑脚脱空时,局部应力增大系数见式(6):

当采用12组支撑,局部一组撑脚脱空时,局部应力增大系数见式(7):
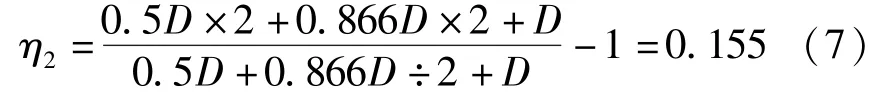
当η1=0.414及h=8 mm时,根据图7,采用线性内插得,滑道安装最大误差Δ=0.442 mm,因此,滑道局部安装平面可按照小于0.5 mm控制。
当采用8组支撑,仅一组撑脚受力时,局部应力增大系数见式(8):

当采用12组支撑,仅一组撑脚受力时,局部应力增大系数见式(9):
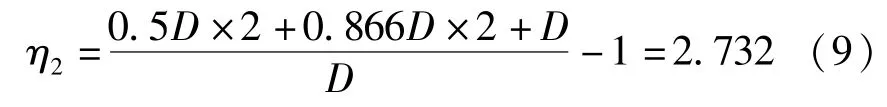
当η1=2.732及h=8 mm时,根据图7采用线性内插得,滑道安装最大误差Δ=2.914 mm,因此,滑道同一水平面整体安装平面可按照小于3.0 mm控制。
5 结论
本项目桥梁已完成RPC球铰的加工、制造及安装工作,于2020年8月成功完成转体施工,并得以下研究结论:
(1)根据球铰构造,分析了球面和平面的比值与球冠高度H、半径r的关系,球铰的应力计算方法,可近似参照平铰进行计算。
(2)结合球面应力误差计算方法,分析研究了球面半径误差对球铰应力的影响,球铰半径误差宜控制在8 cm以内。
(3)根据球铰承压面应力误差计算方法,分析研究了球面局部误差对球铰应力的影响。
(4)参照支座竖转角度,研究了上下球铰安装控制标准,要求上下球铰间隙小于2 cm。
(5)结合撑脚作用特点,研究了滑道安装控制标准。整体安装误差要求小于3.0 mm、局部安装安装误差要求小于0.5 mm。
RPC球铰具有半径小、体积小、重量轻、运输安装便捷等诸多优点,从而可以较大地优化下部结构尺寸,降低工程造价,具有良好的适用前景和推广价值。
