生产网络与行业收益率:基于时变网络依赖参数的空间因子模型
2022-08-02石泽龙
石泽龙 ,傅 强 ,李 山
(1.重庆大学 经济与工商管理学院,重庆 400044;2.重庆联合产权交易所集团股份有限公司博士后科研工作站,重庆 401129;3.中国人民大学 公共管理学院,北京 100872)
过去20年中国经济高速发展,行业间通过投入产出关系形成复杂且紧密关联的横截面关系即生产网络(或称为供应链网络)。在该生产网络的作用下,行业的异质性冲击会通过网络放大并传递至其他行业形成系统性风险[1-2],进而对资产价格产生深远影响。因此,探讨生产网络对中国行业收益率的影响,具有重要的学术价值和实际意义,它不仅有助于丰富中国资产定价研究视角,而且能有助于政策制定者强化市场的配置功能,进而建立高标准市场体系以服务高质量发展。
依据资本资产定价模型(CAPM)和套利定价理论(APT)发展起来的传统因子模型,主要是利用少数共同因子来解释资产收益率,但这种依据分散化理论所产生的模型忽视了微观或局部冲击所产生的累计作用,造成因子模型无法捕捉资产收益率的所有横截面关系[3]。众多研究证明,微观或局部冲击通过网络溢出效应会对宏观经济和金融产生不可忽视的影响[4-5]。并且,Zareei[6]证明在网络出现的情形下,资产组合分散化能力将被降低。因此,因子定价模型的理论基础受到了很大的挑战。从计量角度来看,忽视了资产间的横截面关系可能会造成传统因子模型误设(例如内生性问题),进而影响收益率对因子的风险暴露的估计[7]。另外,忽视资产间的横截面关系,会混淆对风险暴露的解释,即混淆系统性风险的来源[8]。因此,如何在传统因子模型中嵌入资产间的横截面关系,并探讨系统性风险的来源是当前资产定价的一个重要研究领域。
本文首先依据《国民经济行业分类》标准和证监会《上市公司行业分类指引(2012版)》对相关年份的投入产出表进行调整形成供给矩阵,并将其标准化得到生产网络。所得生产网络为时变非对称矩阵,且矩阵中的元素反映了一个行业对另一行业作用的力度及方向即加权有向网络,尽可能还原经济现实且捕捉了不同时期行业变化情况。其次,将生产网络作为空间加权矩阵嵌入因子模型,并假设网络依赖参数为时变,构建了基于生产网络的时变空间因子模型。该方法包含行业间的横截面关系,在一定程度上避免了传统因子模型所产生的误设问题,且假设网络依赖参数时变,能更有效地捕捉时变生产网络对行业收益率的影响。最后,借鉴Acemoglu等[9]提出的分解方法将行业收益率对因子的总风险暴露分解为直接风险暴露和间接风险暴露,以探索各因子风险暴露的来源。研究发现:①对于中国行业收益率而言,相比传统因子模型,采用空间因子模型更符合中国资产定价研究;②假设空间依赖参数为时变参数更符合中国经济现实且模型业绩更佳;③通过对因子风险暴露的分解,发现生产网络溢出效应能放大行业收益率对因子的风险暴露。
1 文献综述
与本文研究相关的文献分为如下几个方面:
(1)生产网络构造的相关文献。随着微观冲击通过网络结构可能会对宏观经济产生累计影响的持续证明,学者们开始关注生产网络的构造,依据构造视角可分为微观和宏观视角。
微观视角主要利用财务报表中企业所公布的供应商与客户数据来建立企业间的相互关联。该视角能有效地将个体企业联系起来,且依据财报公布频率可获得较丰富的研究数据,能很好地应用于资产定价的研究。这方面的研究主要有:Cohen等[10]和Menzly等[11]证实了供应商与客户关系网络能预测美国股票收益率;Herskovic[12]证明了供应商与客户关系网络能够解释长期风险及收益率的横截面;Michael等[13]利用供应商与客户关系数据研究了公司到消费者距离与公司风险之间的关系,实证发现,远离消费者的公司具有更高的风险溢价和对累计生产率更高的风险暴露。然而,供应商与客户信息多属商业机密,中国相关法规并无强制披露要求,囿于信息较难获取,国内研究相对匮乏。
宏观视角主要利用国家统计局所公布的投入产出表来建立行业间的相互关联。鉴于供应商与客户数据难以获得及研究宏观方面的需要,国内学者主要采用此视角构造生产网络。其中,董志勇等[14]和张龑等[15]依据《国民经济行业分类》标准和证监会《上市公司行业分类指引(2012版)》对相关年份的投入产出表进行调整形成供给矩阵,将其转化为对称矩阵并进行稀疏化来构造生产网络。该生产网络属于非加权无向网络,具有时变对称且主对角线元素为零等特征,能够反映行业间紧密关联,但无法反映行业之间相互作用的方向及力度。金融市场中普遍采用加权有向网络[5,16],以便更为真实地反映部门(或行业)间的相互作用。因此,在上述研究思路获得供给矩阵的基础上,本文直接对供给矩阵行标准化得到生产网络。所得生产网络为时变非对称矩阵,且矩阵中的元素反映了一个行业对另一行业作用的力度即加权有向网络,更适用于行业收益率的研究。
(2)网络与资产价格的关系研究。国内外关于网络与资产价格的文献众多,按照网络划分主要包括生产网络[12-13,17]、相关系数网络[18]、机构投资者抱团网络[19]、现金流网络[20]、交叉持股网络[21]及信息网络[22]等。按照计量方法的选择可分为传统资产定价方法和空间计量方法。其中,传统资产定价方法主要是利用网络结构构造相应指标(例如网络集中度等),并将该指标通过长短组合的形式形成网络因子,且结合组合分析方法或Fama Mabetch估计方法来验证所构造网络因子的有效性。该方法的本质是将网络视为一种系统性风险,研究其对资产价格的影响,能够很好地度量网络对收益率的影响,但无法研究其他系统性风险因子与网络之间的反馈作用对资产价格的影响,易混淆系统性风险的来源。
空间计量方法将网络矩阵视为空间加权矩阵,并嵌入因子模型。该方法包含行业间的横截面关系,在一定程度上避免了传统因子模型所产生的误设问题,且可以依据空间效应分解方法研究网络结构对各因子的作用,能够更有效地度量系统性风险的来源。这方面的研究主要有:Bonaccolto等[23]探索了包含因果关系与分位数因果关系的多层网络,并研究其对美国股票市场的影响;Kou等[3]通过将空间作用加入经典资产定价模型提出了空间套利定价理论,其利用国家间的资本距离作为空间加权矩阵,研究了欧洲股票市场。国内关于这方面的研究较少,张玉华等[24]在S-CAPM 模型基础上,利用股票行业分类作为空间加权矩阵,研究了空间面板数据模型对股票收益率的影响,但并没有深入研究系统性风险的来源。与上述文献不同,本文研究时变生产网络对资产价格作用,且假设网络依赖参数时变来刻画中国产业结构变化带来的影响,构建了基于生产网络的时变网络依赖参数的空间因子模型。
(3)生产依赖型资产定价理论的相关文献。本文的研究与生产依赖型资产定价理论相关,这方面的研究主要有文献[25-28]等。这些文献分别从不同角度研究了生产与资产价格之间的关系,但较少关注生产部门之间的相互作用即生产网络对资产价格的影响,仅文献[12-13]中从生产的水平和垂直视角探讨了生产网络对美国资本市场的作用机理。国内关于生产型资产定价的研究较少,朱小能等[29]利用现值模型将生产系统性风险因子分解为现金流贝塔和折现率贝塔,并首次研究了生产型资产定价模型在中国金融市场的适用性,研究表明,生产-现金流贝塔是中国股市的重要定价因子。刘维奇等[30]研究了劳动成本占比对股票市场定价的影响,发现其为显著的定价因子。与文献[29-30]中的研究不同,本文从生产网络视角研究其对资产价格的影响,丰富了中国资产定价的研究视角。
2 空间因子模型
2.1 传统因子模型
考虑如下因子模型:
式中:yt为t时刻N ×1维超额收益率向量;Ft=(f1t,f2t,…,fKt)′为t时刻K×1维共同风险因子向量;B=(β1,β2,…,βN)′为N×K维因子载荷矩阵,βi=(βi1,βi2,…,βiK)为第i个资产对共同风险因子Ft的载荷。
选择不同Ft可得到不同的因子模型:当Ft=(市场超额收益率)时,对应于CAPM 模型(简记为CAPM);当时,对应于Fama French 3因子模型(简记为FF3);当
时,对应于Carhart 4因子(简记为C4);当
时,对应于Fama French 5因子模型(简记为FF5)。
2.2 不变网络依赖参数的空间因子模型
众多研究表明,传统因子模型仅能刻画不可分散的系统性风险,忽视了微观冲击通过资产间网络所带来的累计影响,易造成模型误设(内生性问题),进而影响风险暴露的估计及混淆系统性风险的来源[3,7-8]。空间因子模型通过将资产间网络嵌入传统因子模型,在一定程度上弥补了传统因子模型的上述缺陷。
不变网络依赖参数的空间因子模型建模如下:
式中,yit、Ft及βi=(βi1,βi2,…,βiK)如式(1)所述。空间项刻画了其他资产超额收益率对资产i的同期影响,捕捉了资产间的同期相关性,其中,为超额收益率与空间权重ωij的加权平均值,ρ是网络依赖参数。这些权重形成空间加权矩阵:W=(ωij)i,j=1,2,…,N,且假设对于任意i、j,有ωij≥02)模型允许ωii ≠0(i=1,2,…,N),正如Ozdagli等(2021)所论述,通过简单变换将其变为主对角线元素为零的空间加权矩阵。假设主对角线元素不为零,更符合金融领域的网络结构特征,
为方便分析,将式(2)表示为向量形式:
式中,εt=(ε1t,ε2t,…,εNt)′为误差向量,其均值为零向量,协方差矩阵为:
与式(1)相比,空间因子模型主要增加了ρWyt,将其移至方程左边,并方程两边同时乘以(IN -ρW)-1即可转换为简化形式:其中:
与模型式(1)的关键差别在于简化形式的残差项为(IN-ρW)-1εt,由于W主对角线以外元素可能不为零,故该残差项是空间相关的。传统因子模型因遗漏了资产间的空间依赖性,可能造成风险暴露的估计值出现一定的偏误3)Giglio等(2021)证明遗漏因子可能会造成风险暴露beta及风险价格lambda的估计出现偏误,严重时会影响估计的显著性及符号,且混淆了系统性风险的来源。
2.3 基于生产网络的时变网络依赖参数的空间因子模型
为了研究生产网络对中国因子定价模型的影响,使用投入产出表计算生产网络矩阵。为了更全面地考查生产网络的作用,依据统计局公布的4次投入产出表(2002、2007、2012及2017年)构建时变空间加权矩阵:Wt=(ωijt)i,j=1,2,…,N,以捕捉经济中行业相对重要性的变化。并且,为更全面地捕捉此变化对行业收益率的影响,假设网络结构依赖参数ρt为时变过程,其状态方程服从如下随机游走过程4)假设空间依赖参数服从随机游走过程是构造时变性的一种常用方式:
基于生产网络的时变网络依赖参数的空间因子模型为
将式(5)表示为向量形式:
为了估计模型式(4)与式(6),需要求对任意t时刻都有IN-ρtWt为可逆矩阵。由于Wt为非对称空间加权矩阵,借鉴Aquaro等[31]可证明,当ρt在(1/rt,min,1)上,IN -ρtWt是可逆的,其中,rt,min为Wt的负实数特征值中最大特征值。
2.4 整体风险暴露及分解
针对模型式(5)进行变形可得
式中,α*和如前所述。借鉴传统因子模型,定义在t时刻行业超额收益率对因子的总风险暴露为(IN -ρtWt)-1B。为了探讨系统性风险的来源,借鉴文献[9],利用(IN -ρtWt)-1的泰勒展开式(即(IN-ρtWt)-1=IN+ρtWt+(ρtWt)2+…),将总风险暴露分解为直接风险暴露和网络风险暴露。具体定义如下:
(1)行业超额收益率对因子的直接风险暴露矩阵为B,即总风险暴露展开式的第1项。其中,B=(βk)k=1,2,…,K,βk为N×1维列向量,表示行业超额收益率对第k个因子的风险暴露向量,可以发现,直接风险暴露矩阵是常数,不随t变化。进一步定义平均直接风险暴露为为行业超额收益率对第k个因子的风险暴露的平均值。
(2)t时刻行业超额收益率对因子的网络风险暴露矩阵为总风险暴露减去直接风险暴露[(IN -ρtWt)-1-IN]B,度量了因生产网络的作用使得行业超额收益率对因子的风险暴露。定义平均网络风险暴露为网络风险暴露关于行业i的平均值。进一步定义网络风险暴露比例为网络风险暴露占总风险暴露比例×100,以度量网络风险暴露的份额。
2.5 估计方法的选择
假设网络依赖参数ρt为时变参数,增加了模型估计的难度,因此,借鉴Hauzenberger等[32]的研究,使用贝叶斯估计方法估计模型式(4)和式(6)。其中,对于网络依赖参数ρ0 的初始状态,选择先验对于网络依赖参数的状态新息方差,假设温和的信息逆gamma先验ς2~G-1(cς,dς),且cς=3,dς=0.03;测量方程误差方差指定为独立逆高斯先验1(cσ,dσ),且cσ=dσ=0.01。式(6)所对应的对数似然函数为
2.6 实证设计
研究思路:首先,利用MoranI检验对传统因子模型的残差进行空间相关性检验。由2.2 节所述,空间因子模型与传统因子模型的主要差别在于残差项是否存在空间自相关,因此,有必要进行残差的空间相关性检验。为了防止因残差项含有共同因子导致检验失效,本文考虑更全面的因子模型,即CAPM、Fama French 3因子(简记为FF3)、Carhart 4因子(简记为C4)及Fama French 5因子模型(简记为FF5)5)稳健性检验中考虑了目前国内其他具有影响力的因子,如流动性因子、情绪因子。其次,利用业绩度量指标,比较各因子下的传统因子模型、基于生产网络的不变网络依赖参数的空间因子模型以及基于生产网络的时变网络依赖参数的空间因子模型的业绩。最终,研究得到生产网络对系统风险暴露的影响。
3 生产网络构建及实证分析
3.1 生产网络构建
(1)数据选择。对于生产网络数据的选取,根据《国民经济行业分类》标准、证监会《上市公司行业分类指引(2012版)》对2002、2007、2012和2017年的投入产出表进行统一调整,使得投入产出表中的部门与证监会行业分类标准中的行业尽可能对应,并且在时间趋势上保持一致。为了降低噪音影响,并与行业股票收益率数据保持一致,通过合并、删除等调整方式最终得到54个有效行业(见附录A)。另外,由于投入产出表数据一般在调查后第3年公布,且其能够准确度量反映一段时期行业间经济联系,对于每一调查年份的投入产出表,将其与调查后的1~4年对应,目的是尽可能还原经济现实的同时能够捕捉不同时期行业变化情况。
选择A 股全体股票,且对股票收益率数据做如下处理:①对于证监会规定的特殊状态(ST、*ST、PT、退市)股票进行删除;②对于IPO 现象,为消除新上市股票价格异常行为对结果的影响,删除所有股票上市后最初120个交易日的交易数据[33]。依据构建生产网络数据中的行业划分,结合证监会《上市公司行业分类指引(2012版)》对中国上市公司进行分组,并依据行业内股票流通市值加权形成各行业月度收益率。在此基础上,减去无风险利率得到所选行业的月度超额收益率,其中无风险利率为人民银行公布的人民币3 个月整存整取利率。由于2000年以前上市公司数量不足1 000家,为确保足够多的股票数量且鉴于投入产出表数据自2002年开始,本文选择数据区间为2002-01~2021-036)后面对其进行稳健性检验,检验结果类似,以便更全面地研究生产网络下的因子定价模型。数据来自国泰安和锐思数据库。考虑到极端值可能引致的偏差,对所有连续性变量在1%和99%水平上进行缩尾处理。
(2)构建生产网络。为了构建生产网络并识别行业关联,主要使用投入产出表中最核心的部分,即由各部门的中间投入与中间使用交叉形成的部分。由于投入产出表行与列部门名称、数量、顺序完全对应,故中间投入与中间使用交叉形成N阶方阵Z,N为部门数量。方阵中的每个元素zij表示部门j对部门i的直接消费总额。借鉴文献[14-15],使用矩阵Z中的zij除以行业j的总投入得到标准化矩阵S。供给矩阵S中的每个元素反映了j部门生产单位产品对i产品的直接消耗。与上述文献不同,本文直接将标准化矩阵S进行行正规化,得到生产网络所需的空间权重矩阵。所获得的空间权重矩阵是非对称时变,且主对角线元素不为1,每行之和为1,这有利于本文研究网络传染效应对行业收益率的影响。
由2017年的生产网络(见图1)可知,石油和天然气开采业、铁路、船舶、航空航天和其他运输设备制造业、专用设备制造、铁路运输业、水上运输业、道路运输业以及商务服务业专业技术服务业等行业处于网络的核心,而畜牧业、农副食品加工业、纺织业、化学纤维制造业以及废弃资源综合利用业等行业处于网络的边缘。
3.2 模型估计及评价
(1)传统因子模型残差的空间相关性检验。正如2.2节所述,空间因子模型简化形式与传统因子模型的核心差别在于传统因子模型的残差项是相互独立的,即传统因子模型不存在空间相关性。借鉴空间计量经济学的研究思路,采用Moran’sI统计量检验传统因子模型的残差是否存在空间相关性。由于本文选择的时变生产网络已进行行标准化,故Moran’sI可以表示为:其 中:et为t时刻N个行业的残差向量,其维度为N ×1;Wt为t时刻的生产网络矩阵。Moran’sI空间相关性检验的原假设为:H0:Y=Xβ+ε,即不存在空间相关性。在零假设E[I]=0下,Moran’sI检验为为了消除因遗漏共同因子造成残差相关的影响,选择CAPM、FF3 因子、C4因子及FF5因子模型进行检验。
通过估计CAPM、FF3因子、C4因子及FF5因子模型得到相应的参数估计,并计算各模型残差的空间相关性检验,结果如表1所示。由表1可以发现,从54个行业平均来看,市场超额风险、SMB 所对应系数是显著的,而其他因子并不显著。另外,依据Moran’sI检验可以发现,在95%置信区间上,所有模型存在显著空间相关的个数均达到226 以上,占比达0.98,其中整个样本为231,表明绝大部分时间各传统因子模型的残差项存在空间相关性。这充分说明,传统因子模型忽视了空间相关性,造成模型存在非常大的误设风险,进而可能导致对因子的风险暴露(beta)的估计存在偏误。

表1 模型估计结果
(2)空间因子模型的估计结果。由空间相关性检验发现,传统因子模型的残差存在一定的空间相关性,易造成误设模型,故选择空间因子模型。为准确估计,使用贝叶斯估计方法,利用包含向前滤波向后抽样(FFBS)的MCMC抽样算法得到条件后验分布。具体结果如表2所示。
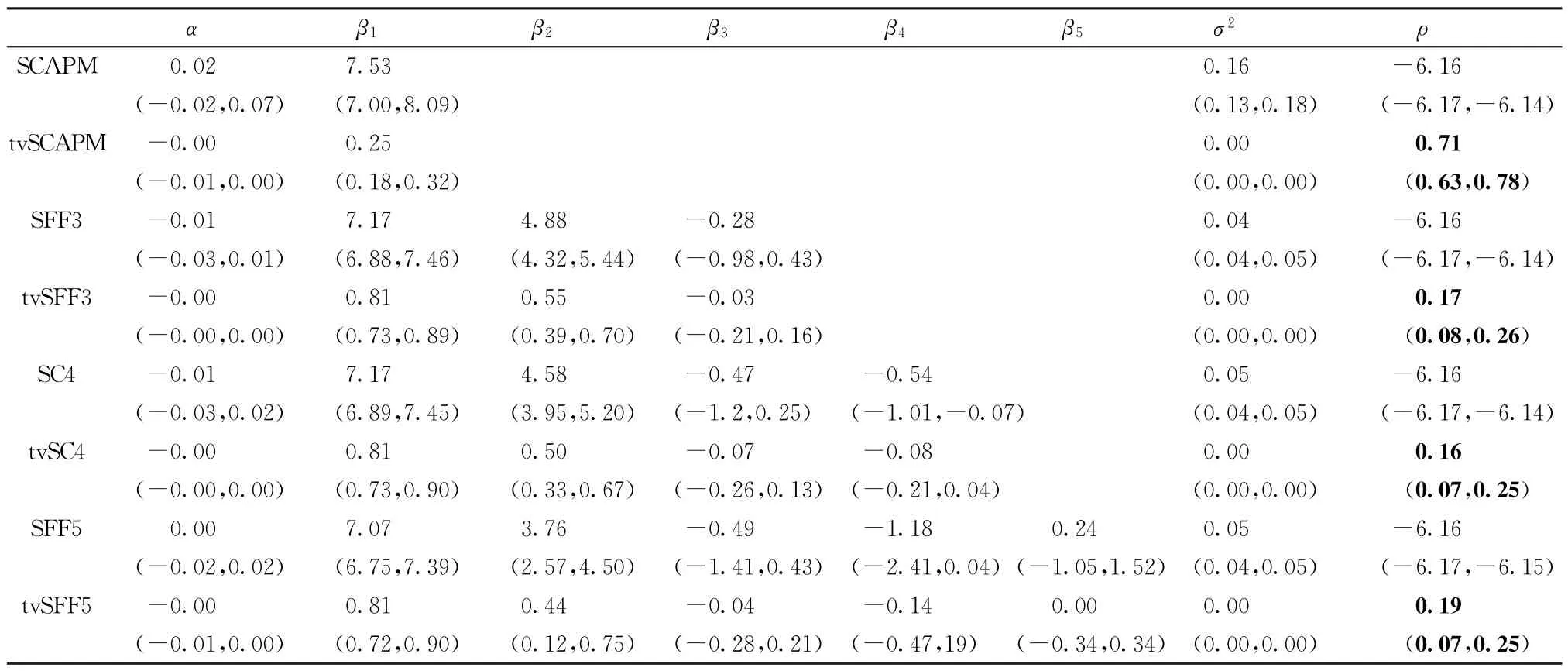
表2 空间因子模型的估计结果
首先,考虑基于生产网络的不变空间因子模型(SCAPM、SFF3、SC4 及SFF5 模型)的估计结果。由此发现,各模型的网络依赖参数(ρ)的估计值均为负值,95%置信区间上显著,且满足IN -ρWt为非奇异的条件(见附录B)。由于网络依赖参数表示各资产对来自相邻资产的冲击在横截面和时间上的平均反应,其估计值为负表明其他行业收益率对该行业的影响是负的。这与经济理论不符,理论上,行业间联系越紧密,某个行业的局部冲击会通过网络放大效应更容易形成系统性风险,投资者承担此风险需要更高补偿,因此,预期未来具有更高收益率。并且,因为yt与Wtyt的相关性为正7)计算皮尔逊相关系数发现,54个行业超额收益率与空间项的相关系数均大于0.5,最低为0.68。限于篇幅,未列相关系数表,所以网络依赖参数估计值为负不符合研究事实。究其原因是,近20年中国产业结构发生了重大变化,假设网络依赖参数为常数则无法刻画生产网络变化对行业超额收益率的影响。
其次,考虑基于生产网络的时变空间因子模型(tvSCAPM、tvSFF3、tvSC4及tvSFF5模型)的估计结果。由表2可以发现,在控制其他因子的情形下,网络依赖参数估计值的均值位于0和1之间,且在95%置信区间上显著。绘制各模型网络依赖参数估计值的时间序列变化情形(见图2),发现大部分时期各模型的ρt估计值均显著大于零且随时间变化幅度较大,而其他时期估计值虽为负但在95%置信区间上不显著,且各模型ρt的估计值均满足IN -ρtWt为非奇异条件(见附录B)。这说明,假设时变的网络依赖参数是合理的,符合中国资产定价的研究,也表明了行业收益率对各因子的风险暴露部分来自于更高阶的网络效应。另外,各模型ρt的估计值变化趋势基本一致,唯独tvSCAPM 模型的估计值差别最大,主要原因是,tvSCAPM 模型仅包含了市场超额收益率,可能遗漏了其他重要的解释变量,而该解释变量与空间项相关。
(3)各模型业绩评价。假设资产定价模型能够完全捕捉预期收益率,则截距项α应不显著异于零。由于GRS统计量仅适用于线性因子模型[34],无法用于检验空间因子模型,故选择如下指标对比各模型的优劣:①截距项的平均L1范数A(|α|);②截距项的平均L2范数A(α2);③均方误差(RMSE)。其中,前两个指标为截距项α的一阶、二阶[35],反映了行业收益率中不能被模型所解释部分的规模,第3个指标使用误差项进行评价能直接反映模型对行业超额收益率的偏离程度。上述3个指标在不同程度上度量了行业收益率不能被风险模型所解释的比例,越小表明模型拟合效果越好。具体结果如表3所示。

表3 模型业绩对比
依据上述指标发现,对于各因子而言,基于生产网络的时变空间因子模型的业绩最好,其次为传统因子模型,最次为基于生产网络的常数空间因子模型。这主要是因为,相比发达国家,近年来中国产业结构发生了重大调整,造成依据投入产出所形成的生产网络也发生了较大变化,此时假设空间依赖参数ρ为常数不符合经济现实,也导致了基于生产网络的不变空间依赖参数的空间因子模型业绩较差的事实。相反,考虑空间依赖参数时变的空间因子模型,能更好地捕捉生产网络溢出效应的改变,因此业绩更好。同时,与传统因子模型业绩相比,嵌入生产网络的时变空间因子模型有助于提高业绩。这说明,生产网络溢出效应对因子模型具有一定的作用。
3.3 基于生产网络的时变网络依赖参数的空间因子模型的网络效应分析
(1)平均效应分析。为探讨生产网络溢出效应对中国因子定价模型的作用,依据式(7)计算了行业收益率对各模型因子的平均总风险暴露,并将其分解为平均直接风险暴露和平均网络风险暴露(见表4)。tvSCAPM、tvSFF3、tvSC4和tvSFF5模型中超额市场收益率因子的平均网络风险暴露分别为0.77、0.19、0.18和0.17,占平均总风险暴露比例分别为75.52%、19.00%、17.84%和17.33%,均为正且显著。这表明了生产网络放大行业收益率对市场风险因子的风险暴露,投资者承担市场风险,需要更高的溢价作为补偿。另外,tvSCAPM 模型中市场风险因子的平均网络风险暴露及占整体效应比例与其他模型相差较大,可能是由于该模型遗漏了其他重要风险且该风险与空间项Wtyt存在显著正相关8)许多文献已经证明在A 股市场上,三因子、五因子等模型比CAPM 模型更具解释能力[30,33]。

表4 基于生产网络的时变空间依赖参数空间因子模型的直接效应、网络效应分析
同样,各模型中SMB 的平均网络风险暴露分别为0.13、0.11和0.09,占平均总风险暴露比例分别为19.19%、18.33%和17.48%,均为正且显著。这也说明,生产网络放大行业收益率对SMB 的风险暴露,投资者承担该系统性风险,需要更高的溢价作为补偿。
与市场风险和SMB 因子不同,各模型中HML、动量因子(UMD)及投资因子(RMW)的平均网络风险暴露均为负、占比为正且显著。由于总效应为负,这表明,生产网络放大了行业收益率对HML、UMD 及RMW 的风险暴露,投资者愿意为套保此类风险支付更高的溢价。而tvSFF5模型中盈利因子(CMA)的直接暴露、平均网络风险暴露、总风险暴露及占比均不显著,表明生产网络对该因子没有显著影响。同时,这也与李志冰等[33]的研究结论一致,可能是因股权分置问题扭曲了中国资本市场定价机制,使得CMA 呈现出冗余现象。
(2)直接效应和网络效应的时变性分析。在生产网络和网络依赖参数时变的情形下,行业收益率对各因子的总风险暴露、网络风险暴露也随时间变化,而直接风险暴露保持不变。以tvSFF3 模型为例,分析行业收益率对市场风险、SMB 及HML 的风险暴露(见图3~5)。各图从上至下实线分别表示总风险暴露、直接风险暴露、网络风险暴露及百分比(网络风险暴露/总风险暴露×100),其中阴影部分表示置信度为95%的置信区间。由图3~5可知行业收益率对市场风险、SMB的网络风险暴露分别在0.19和0.13上下波动,占总风险暴露的比例分别在19.00%和19.19%上下波动;而行业收益率对HML的网络风险暴露为负且在-0.01上下波动,占总风险暴露的比例在19%上下波动。
综上所述,行业收益率对各因子的网络风险暴露时变、占总风险暴露比例均达19%且显著。这表明,生产网络具有放大行业收益率对因子的风险暴露的作用。究其原因是:某行业收益率对因子的风险暴露,既来自于该行业收益率对风险因子的直接暴露,又来自于因生产网络使得各行业收益率相关,进而来自于其他行业收益率对该因子的风险暴露传染至该行业,通过这种反馈效应使得生产网络信息溢出放大了行业收益率对因子的风险暴露。
3.4 稳健性检验
(1)时变空间因子模型的分时检验。股权分置问题造成了流通股股东与非流通股股东之间长期存在利益分割[36],严重扭曲了中国资本市场的定价机制[37-38],可能对本文结果产生一定的影响,因此,本文考虑股权分置改革后的样本(2007-01~2021-03,共计165个)做稳健性检验,检验结果见附录C。由附表3~5可以发现,股权分置改革完成后,传统因子模型仍然存在一定的空间相关性,且基于生产网络的时变空间因子模型能够提高解释业绩,与前面结论基本一致。
(2)其他因子模型的检验。3.2节通过MoranI检验证明CAPM、FF3、C4及FF5因子定价模型的残差均存在空间相关性,那么,是否这些模型遗漏了重要的解释变量造成残差存在空间相关性? 为回答此问题,将中国资产定价研究中常用的流动性因子、情绪因子嵌入,进行稳健性检验,相关结果见附录D 中附表6~8。发现:加入流动性因子、情绪因子的传统因子定价模型的残差仍然存在空间相关性,且基于生产网络的时变空间结构依赖参数的空间因子模型业绩更佳,与前面结论基本一致。
4 结论
将生产网络嵌入传统因子定价模型,结合中国产业结构出现重大调整的事实,构造了时变空间因子定价模型,并借鉴Acemoglu等[10]提出的分解方法将行业收益率对因子的总风险暴露分解为直接风险暴露和间接风险暴露。主要结论如下:
(1)通过对传统因子定价模型(CAPM、FF3、C4及FF5)的残差进行检验,发现均存在显著的空间相关性,并且基于生产网络的时变空间因子模型估计所得的网络依赖参数显著。这说明,对于中国行业收益率而言,采用传统因子定价模型会导致模型误设,而采用空间因子模型更符合中国资产定价研究。
(2)通过3个业绩指标分析发现,对于各因子模型而言,基于生产网络的时变空间因子模型的业绩最佳,其次为传统因子模型,最次为基于生产网络的常数空间因子模型。主要原因是,相比发达国家,近年来中国产业结构发生了重大调整,生产网络也发生了较大变化,使得假设空间依赖参数时变更符合中国经济现实。
相比传统因子定价模型,基于生产网络的时变空间因子模型更符合中国行业收益率的研究,说明生产网络的溢出效应对中国资产价格具有一定的解释能力。这与近期从生产角度研究中国资产定价的文献相印证,同时丰富了中国资产定价的研究视角——生产网络视角。
(3)通过对因子的风险暴露进行分解,发现行业收益率对各因子的网络风险暴露时变、占总风险暴露比达17%以上,且均显著。这说明了生产网络的溢出效应能放大行业收益率对因子的风险暴露,同样说明传统因子定价模型会低估因子的风险暴露的绝对值。对于政策制定者而言,正确理解资产对各系统性风险的暴露是制定相关政策的前提。
附录A
所选行业。

附表1 所选行业名称及序号
附录B
网络依赖参数的可行范围。

附表2 网络依赖参数的可行范围
附录C
股改后样本的检验。

附表3 模型估计结果

附表4 模型估计结果

附表5 模型业绩对比

附表6 各模型估计结果及检验
附录D
其他因子的检验。

附表7 空间因子模型估计结果
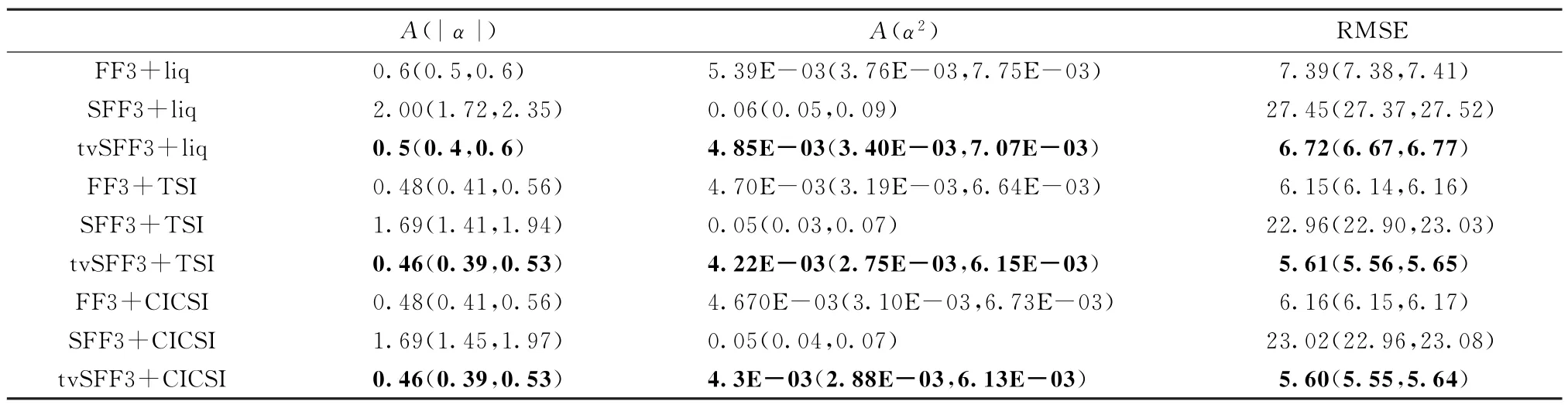
附表8 模型业绩比较
