基于虚假数据注入攻击的网络安全检测

胡凯波，於立峰，郑美芬，崔 娜

（浙江浙能兰溪发电有限责任公司，浙江 金华 321100）

智能电网的深度融合，提升了电网的整体调度能力和效率。但伴随5G、人工智能和大量终端设备接入，信息物理融合系统（Cyber-Physical System，CPS）网络的安全风险也在不断增加。由于CPS由感知层、传输层和应用层构成，所以针对CPS的攻击类型复杂多样，如虚假数据注入攻击（False Data Injection Attacks，FDIA）［1］、拒绝服务攻击［2］、传感器欺骗攻击［3］、重放攻击［4］以及恶意软件访问隐私数据攻击［5］等。在以上攻击类型中，以FDIA攻击最为常见，破坏性最强。攻击者篡改传感器量测数据，或删除量测数据，造成决策系统发出错误决策，进而严重威胁CPS网络安全。针对CPS的虚假数据注入攻击，王电钢［6］、王羽［7］等从博弈论的角度就攻防过程进行建模，并构建防御策略，以提高CPS网络的安全性；阮兆文［8］等针对FDIA攻击中的数据篡改问题，提出一种基于聚类算法与状态预测的检测方法，该方法的本质是基于状态估计；陈碧云［9］、刘鑫蕊［10］等则针对量测冗余度低给CPS带来的威胁问题，提出自适应无迹卡尔曼滤波动态估计结合神经网络的攻击检测方法，结果显示可有效提高攻击检测的辨识率；魏书珩等［11］也提出一种基于状态估计的FDIA攻击检测方法。以上研究都是从数据篡改给CPS网络带来的稳定性、安全性影响方面进行分析，进而躲避传统攻击检测机制中的攻击向量设计问题。针对攻击向量设计的假设，使攻防两方对CPS网络拓扑结构、传感器量测分布等均知晓，但实际中电网企业会采取各种攻击防护措施，因此不可能完全知晓网络拓扑结构和量测分布，很难建立攻击模型。同时研究认为，电网节点和攻击向量都呈正态分布［12］。基于该分布特性，结合攻击者恶意注入的攻击向量和系统采集数据，提出一种基于高斯混合模型结合机器学习的网络攻击检测方法，并就该方法的正确率等进行验证。

1 高斯混合模型（Gaussian Mixture Model，GMM）

GMM原理如图1所示。该模型是基于一个概率密度函数，即设全部数据点X={x1，x2，...，xN}为同一密度函数中独立抽样得到的，且该概率密度函数为高斯函数的组合，具体表达式为［14］

式（1）中，ωm表示数据点xi产生于第i个高斯成员的先验概率，，且∀m=1，…，K；G(xi；μm，∑m)为高维高斯函数。

根据式（1），只需根据观测的数据点，求解式（1）中的参数ΘK，其中Θm={αm，μm，∑m}。由此，根据以上描述，就将无监督学习问题直接转换为概率中的参数估计问题。而针对参数估计问题，通常采用极大似然估计方法。

2 基于高斯混合模型的FDIA检测模型构建

2.1 攻击检测模型整体流程

实践认为，FDIA检测算法精度受状态估计精度的影响［15］。但状态估计的精度受两方面影响：一是攻击向量的攻击强度。一般来说，检测算法对攻击强度较大的攻击向量更具敏感性；二是检测阈值。该值通常是根据经验设定，它对于检测算法精度起到关键影响。由于电力系统节点的电压服从高斯分布，因而攻击构造的虚假数据注入攻击向量也服从高斯分布。在最优潮流条件的约束下，电网节点电压状态数据分布较为集中，而攻击向量却较为分散。据此，除要构造2种不同的高斯分布外，还要引用高斯混合模型。考虑到智能电网未受攻击和遭受攻击的传感器量测数据分别服从不同的高斯分布，因此采用高斯混合模型对两组量测数据的分布特征进行拟合。基于高斯混合模型聚类的FDIA检测流程如图2所示。首先，根据遭受攻击前后的传感器量测数据分布特征，利用采集的最优潮流数据，构造正负样本数据，然后利用训练集数据对GMM参数进行训练，获得优化后的GMM参数；利用测试样本数据对GMM分类效果进行检验，看是否可准确识别虚假数据注入攻击；最后，通过仿真实验对构建的攻击检测效果进行验证。

2.2 GMM具体构建

依据智能电网节点电压和攻击向量服从正态分布的规律，将所有的量测数据分为正常和异常，这两种数据分别属于不同的高斯分量，同时通过这两个高斯分量构成高斯混合模型。设某时刻的测量向量服从多维度的高斯分布，那么测量序列为

将测量序列构造为高斯混合模型，通过K个高斯分布向量加权求和，得到

式中，pi(x)表示高斯混合模型的各个分量；ωi表示各分量所对应的加权系数；xn(t)表示D维传感器测量的特征矢量。

pi(x)根据高维高斯函数，可表示为

由于高斯混合模型的各分量相互独立，所以可用对角矩阵的形式来表示协方差矩阵。

对式（5）进行整理，得到

式（6）中，d={1，2，…，D}。

2.3 GMM参数估计

利用传感器样本数据对GMM进行训练，即利用EM算法对各个分量模型参数进行估计，从而获得一组最优的GMM参数。具体求解步骤如下所示：

（1）建立完整样本集似然函数。

（2）对似然函数的期望进行求解。

将式（8）展开，则有

（3）计算使似然函数取得最大值的混合模型参数。

特征向量属于第l个隐状态的概率为

由此根据式（10），确定加权系数、均值、方差等参数。

通过以上计算，得到GMM的最优参数，并在最优参数下，对测试的量测数据进行分类。

2.4 虚假数据注入攻击检测分类准则

在构建的GMM基础上，将待检测数据最大后验概率设定为判别准则，然后利用软分类法对测量值进行检测，以达到检测分类的目的。因此，设智能电网中的K个检测量所对应的高斯模型参数依次是λ1，λ2，…，λk-1，λk，待检测数据特征向量Z=(z1，z2，…，zT-1，zT)属于第i个高斯分量的后验概率为

测量矢量的最大后验概率密度函数为

根据最大后验概率密度，对测量矢量进行归类。其中，i*表示该测量属于第i个高斯分量。由于测量矢量属于某一高斯分量的先验概率是未知的，因此需进行初始化，假定先验概率是相同的，由此，式（15）可表示为

利用最大对数似然函数进行求解。取对数似然函数，则有

最终分类的判别准则为

利用式（18）的判别准则，对待检测数据进行归类，实现正常数据与虚假数据的分离，从而达到攻击检测的目的。

3 仿真验证

3.1 仿真平台与检测评价指标

为验证上述检测方法的准确性，在IEEE-18节点测试系统上搭建仿真验证平台，用以验证本文提出的基于GMM的FDIA检测效果。同时为对比GMM的优劣，将SVM算法与GMM算法进行对比。

参考部分研究成果，分别以TP、TN、FP、FN表示真阳性、真阴性、假阳性、假阴性，然后采用Accuracy进行评价。若训练样本数据中包含同等数量的未受攻击和遭受攻击数据，此时的检测准确率为

3.2 IEEE-18节点系统检测结果

3.2.1 基本数据

以IEEE-18节点系统为例，该系统内置17条支路和18个节点，包含节点注入功率、支路端口功率、母线节点电压幅值等多个测量值。其中，IEEE-18系统母线节点注入功率如表1所示。

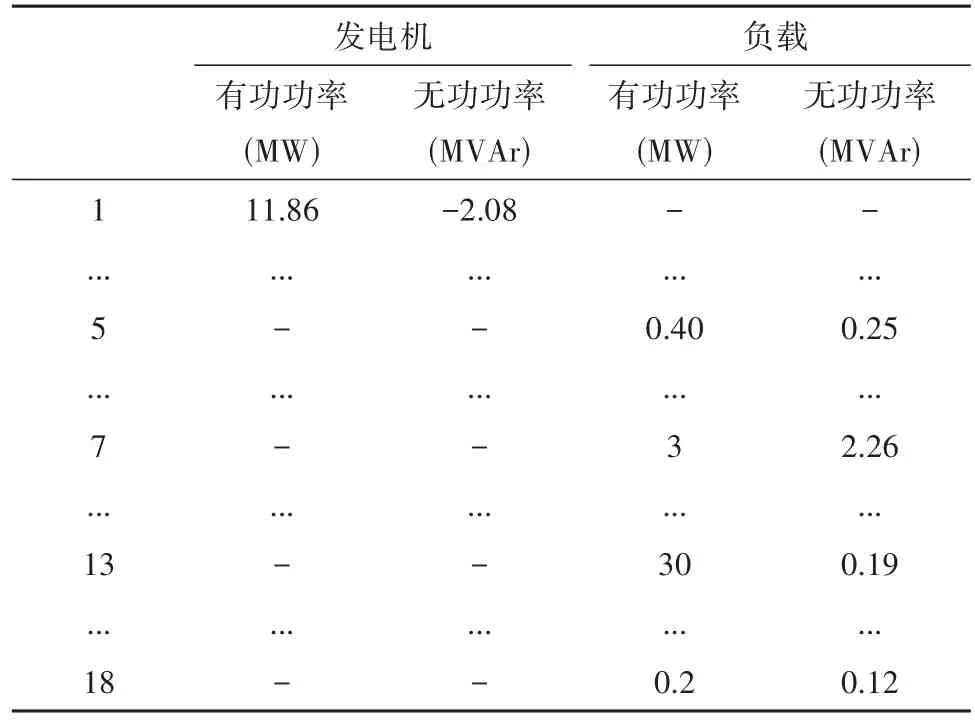
表1 IEEE-18系统的母线节点注入功率Tab.1 Bus node input power of IEEE-18 system

在现实场景中，由于智能电网处于动态平衡状态，发电量与负荷调配都会对系统节点参数造成影响。因此本次仿真将最小成本设定为目标函数，由此得到节点的最优潮流。另外结合电力系统量测方程，将叠加方差等于R的测量噪声设为传感器量测数据，并利用Matpower计算状态向量。在不同攻击强度条件下生成攻击向量，并叠加到传感器的量测数据中，用作传感器在智能电网遭受攻击时所采集的数据。同时设定攻击样本数据与未受攻击样本数据均为300个。利用样本数据对高斯混合模型进行训练，其中攻击强度等于测量值的50%，正常测量向量与非正常测量向量的协方差矩阵分别为

3.2.2 GMM训练结果

GMM参数估计结果如表2所示。

表2 GMM参数估计结果Tab.2 Estimation results of GMM parameters

由表2可见，IEEE-18系统节点电压呈递增态势，因此攻击值也表现出递增趋势。在量测数据统计特性一致的情况下，在节点3以后的混合模型权值均超过了0.5。

3.2.3 分类结果

利用训练后的GMM参数，并依据准则对样本数据进行分类，在节点8以后的聚类效果如图3所示。

由图3的分类可见，训练后的GMM能够将样本数据完全分离开。为更好地验证该模型，提高量测数据之间的离散度，改变状态协方差矩阵对角元素的数量，设定攻击向量和未受攻击测量值的数量均为5000个，利用训练后的高斯混合模型对叠加后的样本数据进行分类，得到图4的分类结果。

由图4可见，本文提出的检测成功完成了测试集数据的聚类，并且准确检测出坏数据。

3.2.4 IEEE-18系统下不同算法的对比

对比基于高斯混合模型的检测方法与基于支持向量机的检测效果，从而验证本检测方法的优势，对比结果如图5所示。

由图5-6可见，两种检测算法在不同的攻击强度条件下表现出大体相当的检测准确性，但若兼顾测量值的统计特性，可发现基于高斯混合模型的检测算法在检测精度方面具有更优性能。

4 结 语

通过以上研究可以看出，通过构建GMM，实现了智能电网的虚拟数据注入攻击检测，且大幅度提高了检测的精度。而通过仿真也看出，GMM的检测精度，受攻击强度和协方差矩阵的影响。因此，要提高GMM分类的精度，关键要对以上参数进行优化。