实时彩色图像自适应中值滤波算法的FPGA实现
2022-08-02韩玉鑫王晓凯陆金旺
韩玉鑫,王晓凯,陆金旺
(山西大学 物理电子工程学院,太原 030006)
0 引言
数字图像在采集、传输和处理的过程中,由于设备工作环境的恶劣,会引入一些随机、离散噪点,降低了图像质量和视觉效果[1-2]。现实环境中存在多种图像噪声,如高斯噪声、随机噪声、瑞利噪声等[3],图像降噪应兼顾降噪效果和细节保留这两方面。
目前对椒盐噪声的滤除,有加权中值滤波算法[4]、开关中值滤波算法[5]、自适应中值滤波算法[6]和改进型中值滤波算法[7-10],自适应中值滤波算法运算量大、复杂度高,虽然在PC端可以达到很好的滤波效果,但由于其串行计算的特点,很难满足对高分辨率、高速图像实时滤波的要求。FPGA (Field Programmable Gate Array)为半定制电路,可通过流水线等操作实现面积与速度的互换,可直接将算法映射为电路,从而可极大加快算法执行的效率[11-13]。目前彩色图像的中值滤波主要是将RGB彩色空间转换到YCbCr彩色空间,然后对Y分量进行滤波。由于YCbCr色彩空间会损失掉色度信息,因此降噪后的图像会产生失真。
鉴于此,结合HSI(Hue Saturation Intensity)色彩空间特点设计了一个基于FPGA的实时彩色图像自适应中值滤波系统,极大的增强了滤波的实时性。最终实验结果表明该系统可对2 k(2 560×1 440) @60 Hz彩色视频实时处理,且滤波后图像色彩还原度高,具有广阔的应用前景。
1 RGB-HSI模块
本节将介绍HSI彩色模型,并将几何推导算法和分段定义算法在FPGA硬件上实现。
1.1 HSI彩色模型
我们观察物体时,用其色调、饱和度和亮度来描述这个物体。HSI彩色模型可从携带彩色信息(色调和饱和度)的图像中去除强度分量的影响。因此,HSI模型是开发基于彩色描述图像算法的理想工具。如图1所示图(a)为基于圆形彩色平面的HSI彩色模型,图(b)为基于三角形彩色平面的HSI彩色模型。以图(a)为例,白色顶点与黑色顶点相连的轴为亮度轴,饱和度为像素点与亮度轴的距离,色调为像素点与红色轴的夹角,在亮度轴上饱和度为0且无色调。常见的RGB-HSI转换算法共有5种,算法的具体推导和公式可查阅文献[14]获得。由于HSI各分量间相对独立,故可以根据具体应用,将不同算法的HSI公式交叉使用。下节分别在FPGA上实现几何推导算法和分段定义算法,通过对两种方法转化后图像的质量进行对比,在转化精度与消耗硬件资源之间进行权衡,选择合适的算法。

图1 HSI彩色模型
1.2 几何推导法硬件实现
由于FPGA只能进行整数计算,所以将浮点数转换为整数进行计算,由8位2进制数表示[0,1],量化精度为0.003 921。给定一幅RGB彩色图像,每个RGB像素的H分量可由下式得到:
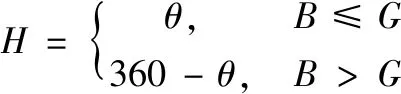
(1)
式中,
(2)
饱和度分量由下式给出:
(3)
最后强度分量由下式给出:
(4)
在硬件中计算arccos(x)比较困难,主要有以下几种计算方式:
1)通过Xilinx官方提供的CORDIC IP核,该IP核可计算arctan(x),利用arctan(x)与arccos(x)转换关系即可完成对arccos(x)的计算。由于在原公式的基础上加入了开方和除法等复杂运算,而IP核直接计算arctan(x)需要20个时钟周期的延迟,所以增大了硬件资源的消耗和处理时延;
2)通过下式:
arccos(x)=
(5)
上式为arccos(x)的泰勒展开式,可通过上式选取合适的n逼近arccos(x),但是当|x|接近1时,上式收敛速度很慢,所需硬件乘法器、除法器和加法器急剧增加,处理时延也会进一步加大,无法满足图像地实时处理;
3)使用ROM查找表的方式实现,将提前计算好的数值从ROM中读取出来,只需要2个时钟周期就可以完成运算,可满足实时图像处理。
为符合处理实时图像的要求,选取ROM查找表方式。当x趋近于1时,由于arccos(x)的导数趋于无穷大,所以arccos(x)会产生较大误差。将x分别量化到[0,255]和[0,4 095],通过这两种量化精度之间的对比,说明上述误差对H分量的影响。
乘法器实现主要分两种情况:在乘一个定值时,为节约硬件资源,采用FPGA擅长的移位运算;在乘一个变量时,为保证系统性能,采用Multiplier IP核实现。除法器实现也分为两种情况,当除数是一个定值时,采用下式实现:
(6)
其中:2n为大于除数的最小整数,m控制计算的精度,m越大精度越高。例如,计算x/3,我们取2n为4,m为8,公式就变为x×341÷1024,乘法采用上述左移方式实现,由于除数为2的整数次幂,除法采用右移相应的位数即可实现。当除数是变量时,采用Divider IP核计算,计算结果将余数舍去,只取商即可。开平方的运算通过调用CORDIC IP核实现。
通过硬件转换与软件仿真结果对比发现,S分量和I分量的误差均在±1以内,而H分量在某些像素点的误差达到20。这是由于硬件计算开平方、除法和反余弦均有误差,而开平方的误差会引入到除法计算中,加大除法计算的误差,除法计算的误差又会被引入到反余弦中,这样会将误差逐级放大。在1.4节会通过具体图片的硬件仿真说明这种误差对色彩空间转换的影响。
1.3 分段定义法与几何推导法相结合
由于HSI各分量相互独立,所以可将分段定义算法与几何推导算法相结合,即H分量通过分段定义法求得,S分量、I分量通过几何推导算法求得,其中上节已完成几何推导法S、I分量的计算,这节主要完成对分段定义算法中H分量的计算,H分量由下式给出:

(7)
式中,θ由下式给出:

(8)
其中:Max=max(R,G,B),Min=min(R,G,B),由于分子的减法会存在负数的情况,所以使用补码进行减法运算。为节约硬件资源,将Divider IP核配置为无符号除法器,这就需要求一个补码的绝对值。当补码的符号位为0时,绝对值为其自身。当补码符号位为1时,可通过2n-complement进行计算,其中n为补码的位宽。下一小节将通过具体图像进行硬件仿真,分别通过MSE(mean squared error)、PSNR (peak signal to noise rate)、SSIM(structural similarity)等评价指标对3种方式生成的HSI进行对比分析。
1.4 硬件仿真对比结果
本节将通过由软件转换后的HSI和FPGA硬件转换后的HSI进行对比,分析上述各种转换方法的差异。如图2所示,其中图a、b、c分别为MATLAB使用几何推导算法转化后的H、S、I分量图,图d、e、f、g、h为通过Modeisim硬件仿真生成的HSI分量图。其中图d、g为几何推导算法H分量的转换结果,它们区别为图d中arccos(x)的x量化精度为0.003 92,而图g中arccos(x)的x量化精度为0.000 244 2。图e、f分别为几何推导算法S、I分量的转换结果,图h为分段定义算法H分量转换结果。

图2 HSI对比图
为了分析硬件转换的精度,分别计算软件与硬件转换结果之间的MSE、PSNR、SSIM[15-16],如表1所示,其中H1为几何推导算法(arccos(x)中x的量化精度为0.003 92) 的色度,H2为几何推导算法(arccos(x)中x的量化精度为0.000 244 2) 的色度,H3为分段定义算法转换的色度,S、I为几何推导法转换的饱和度和亮度。对比3个H分量,分段定义算法转换较为精确,结构相似性可达到99.9%。而几何推导算法即使是将arccos(x)的x量化精度提升至0.000 244 2,相应的结构相似性仅仅从99.68%提升至99.72%,未达到分段定义算法的精度,不仅如此,几何推导法在计算H分量时,进行了复杂函数(开平方和反三角函数)的计算,这些会消耗大量的硬件逻辑资源,而分段定义法最复杂的计算为除法运算,所需硬件逻辑资源较少。分段定义算法H分量结构相似性达到99.9%,几何推导算法S、I分量结构相似性均达到了99.9%,因此本文采用分段定义法计算H分量,几何推导法计算S分量和I分量。
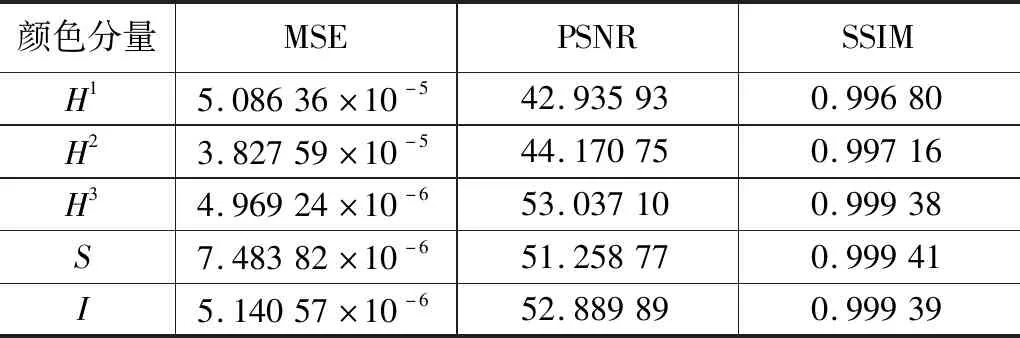
表1 各评价标准对比
2 滤波窗口和排序模块
本节将介绍3×3、5×5和7×7滤波窗口的获取,以及窗口内最小值、最大值和中值的获取,并将其在硬件上实现。
2.1 自适应滤波窗口的生成
本系统自适应中值滤波支持最大滤波窗口为7×7,为实现实时图像处理,此模块直接生成7×7的滤波窗口,3×3、5×5滤波窗口可直接从7×7的滤波窗口得到。为保护图像细节,我们采用扩展邻近像素点的方式对边界进行填充。
我们采用RAM存储图像前6行的数据,而输入的数据作为第7行,这样可以节省一行RAM硬件资源。由于图像分辨率为400×480,HSI分量需要25 bit来存储,其中H为9 bit、S为8 bit、I为8 bit,因此我们需要调用6个位宽为25 bit、存储深度为400的Simple Dual Port RAM。RAM存储时序如图3所示,由于RAM读取数据需要一个时钟周期,所以要将输入像素数据延时一个时钟周期,延时后的像素数据与6个RAM读出的数据构成一个“七行一列”的像素数据。为防止RAM读写冲突,输入的像素数据在RAM1读出数据后写入RAM1中,相应的RAM1读出的数据在RAM2读出数据后写入RAM2中,以此类推。连续缓存7个“七行一列”的像素数据就可以生成7×7的滤波窗口。因为需要等3行像素数据的缓存,所以第一个7×7的滤波窗口与第一个像素相差1 200个有效像素时钟。

图3 RAM存储时序
2.2 排序模块
FPGA是以并行计算为主,通过硬件描述语言实现电路的映射,与单片机顺序操作有很大区别。FPGA实现算法通过触发器和逻辑门电路组合形成电路,更加接近硬件底层的实现,其可在一个时钟周期内完成多个任务,达到并行加速的目的[17]。由于要达到处理实时图像的目的,比较矩阵排序器[18]可以满足实时的要求,该排序器原理为将每一个元素与序列中所有的元素进行比较,大于被比较元素则得分为1,否则得分为0,当所有元素比较完之后,将所得分数进行累加,获得该元素在序列中最终索引值[18]。具体实现步骤为,将序列中的所有元素分别作为一个矩阵的行值和列值,除去对角线上的元素,将每列值分别与每个行值进行比较,并记录每对行列值的比较情况,比较完成后,对矩阵每一行的所得分进行相加,即可得到该行对应元素的最终索引值,但是随着输入元素的增加, FPGA硬件逻辑资源的消耗呈指数增加[18]。由于本文最大输入元素为49,故本文将Priyadarshan Kolte和Roger Smith等人提出的快速中值滤波算法[19]与上述算法相结合,采用流水线方式设计,最大时延为9个时钟周期。下面举例说明该算法排序过程。
假设有一待排序数组{10,10,50,40,30},设D0=10、D1=10、D2=50、D3=40、D4=30,考虑到数组中有相同元素,而且还要进行累加运算。相同元素排序按照原数据谁在前谁优先的原则,即在每个数据与其它数据比较时,根据数据在原数组中的位置,比较器的类型要发生变化[20]。例如Dm与Dn比较时,如果m>n,则选用“≥”比较器,如果m
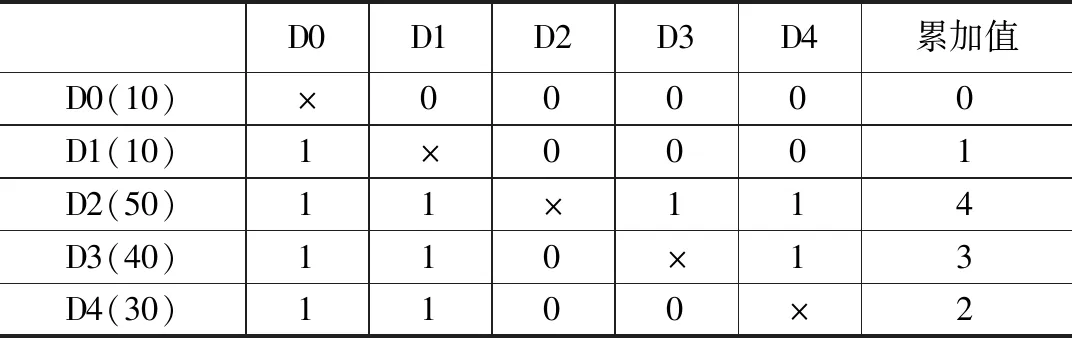
表2 数据比较结果表
对于7×7滤波窗口计算过程如图4所示(箭头所指的方向为升序方向)。

图4 7×7窗口中值获取流程
(1)将7×7滤波窗口中每列像素按照箭头方向做升序排列;
(2)在(1)的基础上将每行像素按照箭头方向做升序排列,则像素点11为最小值像素,像素点77为最大值像素;
(3)在(2)的基础上把45度对角线方向上的5列像素按箭头方向做升序排列;
(4)在(3)的基础上,将像素点27、35、43、51(“+”所在位置的像素点),像素点36、44、52(“-”所在位置的像素点),像素点37、45、53、61(“*”所在位置的像素点),按照箭头方向做升序排列,形成新的7×7滤波窗口;
(5)在(4)处理后的7×7滤波窗口中,取像素点37、44、51的中值,即为7×7滤波窗口内的中值。
其中sort5、sort6、sort7采用上述的比较矩阵排序法(sortx表示对x个元素进行排序),排序需要2个时钟周期。sort3直接采用逻辑门实现,处理需要1个时钟周期。sort4则通过调用sort3,然后将第4个元素插入到合适位置,处理需要2个时钟周期。由于3×3、5×5窗口排序与7×7窗口类似,此处不再赘述。
3 自适应中值滤波
自适应中值滤波算法是根据不同噪声浓度来自适应地调节滤波窗口[21],通过滤波窗口内的极值点来判别噪声与信号。此算法实现需要两个进程,将其中变量表示为:Mmax表示Mxy允许的最大滤波窗口,Imin表示Mxy中的最小亮度值,Imax表示Mxy中的最大亮度值,Imed表示Mxy中亮度值的中值,Ixy表示坐标(x,y)处的亮度值。
自适应中值滤波两个进程如下:
(1) 进程A,A1=Imed-Imin,A2=Imed-Imax,如果A1>0且A2<0,则转到进程B判断原像素点是否为噪声点,否则增大窗口尺寸,如果当前窗口尺寸≤Mmax,则重复进程A,否则输出Imed。
(2) 进程B,B1=Ixy-Imin,B2=Ixy-Imax,如果B1>0且B2<0,则输出Ixy,否则输出Imed。
传统自适应中值滤波算法由于只将局部极值点作为噪声的判定依据,所以此过程很容易造成噪声的误判。由于椒盐噪声集中在HSI彩色模型的亮度轴上,其饱和度是接近于0的,故本文在传统自适应中值滤波算法的基础上,加入S分量进行噪声的判别,可以减少图像细节的丢失。进程A不变,进程B调整为:如果B1=0或B2=0并且S接近0,则输出Imed,否则输出Ixy。
4 HSI-RGB模块
本模块的输入为滤波后HSI分量,目的是实现彩色图像的还原。本节包括了HSI-RGB的转换公式,以及在硬件上的具体实现,同时结合RGB-HSI模块,将一幅图片通过RGB-HSI和HSI-RGB之后,与原图像进行对比,分析其还原精度以及硬件逻辑资源消耗情况。
4.1 HSI-RGB转换公式
公式的选取取决于H的值,在原色分割中有3个相隔120。的扇区(见图1)。当H的值在RG扇区时,即0≤H<120,RGB分量由以下公式[22]给出:
(9)
(10)
G=3I-(R+B)
(11)
H值在GB扇区时,即120≤H<240,RGB分量由以下公式[22]给出:
H=H-120
(12)
(13)
(14)
B=3I-(R+G)
(15)
H值在BR扇区时,即240≤H<360,RGB分量由以下公式[22]给出:
H=H-240
(16)
(17)
(18)
R=3I-(B+G)
(19)
上述的公式具体实现将在下节详细讨论。
4.2 硬件实现
为减少硬件逻辑资源的消耗,可添加扇区标志位,只需实现如下公式即可:
(20)
(21)
c=3I-(a+b)
(22)
通过扇区标志位,根据不同扇区公式将结果分别赋值给RGB即可。对于三角函数的计算,我们采用1.2节中ROM查找表的方式实现。与之不同的是,由于分子分母同时存在余弦函数,可以使用串行方式分别计算两个余弦函数,但是这样会使输出多延时两个时钟周期,所以我们采用同时计算的方式。通过使用Dual Port ROM,这样不仅可以同时完成两个余弦函数的计算,而且所用的ROM资源与计算单个余弦函数相同,可节省一半的ROM资源。可以利用余弦函数的性质,仅仅需要计算[0,90]即可,将计算结果量化到[0,255],这样只需要一个存储宽度为8 bit、 存储深度为91的ROM即可。下节将1.4节中生成的HSI分量通过本模块进行图像的还原,并与原图像进行比较,分析其还原准确度。
4.3 还原精度分析
本节将1.4节中生成的HSI图像通过硬件进行还原,将生成图像与原图进行对比,进一步说明分段定义算法和几何推导算法相结合的转换精度。如图5所示,其中图a为原始图像,图b(arccos(x)中x的量化精度为0.003 92)和图c(arccos(x)中x的量化精度为0.000 244 2)为经过几何推导算法转换后复原的图像,图d为经过几何推导算法和分段定义算法相结合转换后复原的图像,从视觉上难以分辨差别。我们将从MSE、PSNR、SSIM分析复原图像与原始图像之间的差别。
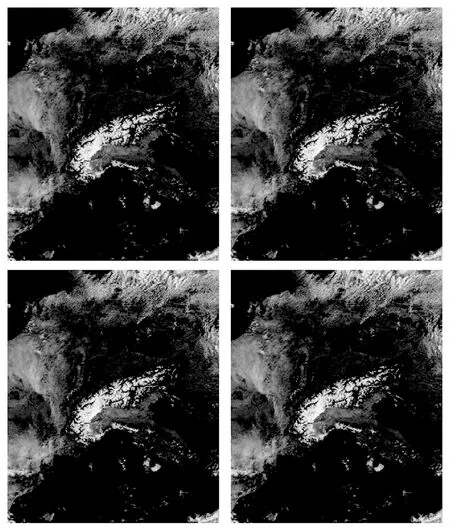
图5 原图与复原的图像
如表3所示,c图的还原精度较b图而言有所提升,但是这种提升是以牺牲较多逻辑资源为代价得到的,结构相似度提高了大约0.7%。相比之下,d图的结构相似度为99.859%,比b图提升了2.872%,比c图提升了2.254%。d图的峰值信噪比为46.87,比b图高9.6,比c图高8.38。不仅如此,几何推导算法和分段定义算法相结合所用硬件逻辑资源比几何推导算法少的多,具体如表3所示,其中LUT减少了37.2%,LUTRAM减少了82%,FF减少了59%,DSP减少了100%。进一步说明了该方法不仅转换精度高,而且硬件逻辑资源消耗较少,适合在FPGA硬件中实现。

表3 复原图像质量以及所用硬件资源
5 系统性能分析
系统结构框图如图6所示,RGB格式数据先经过RGB2HSI模块,将RGB格式转化为HSI格式,处理所需14个时钟周期,其次通过滤波窗口生成模块,处理所需1 200个(以400×480分辨率为例,延时3行像素数据400×3=1 200)时钟周期,接着经过比较排序模块,处理所需9个时钟周期,然后通过自适应中值滤波模块,处理所需1个时钟周期,最后将处理后的HSI数据通过HSI2RGB模块将HSI格式转化为RGB格式,完成对原彩色图像的还原,处理所需27个时钟周期。由于多个模块采用面积换取速度的思想,使用流水线方式实现各模块,故系统处理时间达到了1 251个时钟周期,但这也使得系统支持时钟频率更高。以Xilinx公司的xc7a100tfgg484-2芯片为例,当系统时钟为222 MHz时,Worst Negative Slack(WNS)为0.025 ns,Worst Hold Slack(WHS)为0.043 ns,Worst Pulse Width Slack(WPWS)为1.446 ns,所有的端点都满足时序要求,该系统可以稳定运行。系统最高可对2 k(2 560×1 440)@60 Hz视频进行实时处理,所需像素时钟为2 560(1 440×60=221 MHz,满足系统要求,此时系统时延为14+2 560×3+9+1+27=7 731个时钟周期(1×10-6/222 s),处理时延为347 90 ns。

图6 系统结构框图
通过MATLAB将原图像分别添加不同概率的椒盐噪声,分别将不同概率噪声的图像通过硬件仿真,观察其降噪效果。硬件仿真通过Modelsim进行仿真,在激励文件中,按照bmp文件格式将图片数据读入,并且按照RGB时序输入到系统中,将处理后的图像数据以bmp文件的格式写入。如图7所示,第一行为添加不同概率椒盐噪声的原图像,第二行图为YCbCr彩色空间自适应中值滤波后的图像,第三行为HSI彩色空间自适应中值滤波后的图像。椒盐噪声的概率分别为20%、30%、40%、50%、60%、70%。从中可得出,HSI彩色空间自适应滤波后的图像色彩较为鲜艳,色彩还原度好。当噪声概率小于60%时,降噪后的图像细节保留完整,且无明显的噪声点,当噪声达到70%时,降噪后的图像出现明显的噪声点。

图7 降噪前后图像对比
为了对比不同噪声密度降噪效果,分别计算两种色彩空间滤波后图像与原图像之间的MSE、PSNR、SSIM。如图8所示,当椒盐噪声概率达到70%时,降噪效果明显下降,HSI色彩空间降噪后图像与原图的结构相似度为76.7%。在噪声概率小于60%时,HSI色彩空间降噪后图像与原图的结构相似度均可达到90%以上,而YCbCr色彩空间降噪后图像与原图的结构相似度仅达到80%以上。当噪声概率为10%时,HSI色彩空间降噪后图像与原图的结构相似度可达到99%,而YCbCr仅为86%。当噪声概率小于90%时,HSI彩色空间的各项指标(MSE、PSNR、SSIM)均优于YCbCr彩色空间。HSI彩色空间降噪后图像细节保留完好,未出现图像模糊,达到了在滤除噪声的同时减少细节损失的目的。如表4,为2种不同的彩色空间(YCbCr和HSI)采用相同自适应滤波所消耗的硬件资源,由于HSI为非线性转换,而YCbCr为线性转换,故HSI所消耗硬件资源会更多。但是HSI彩色空间滤波效果提升较大,很好地保留了图像细节,对后续的图像处理影响较小。

图8 滤波后图像MSE、PSNR、SSIM

表4 消耗硬件资源对比
6 结束语
实时彩色图像自适应中值滤波的FPGA实现具有重大的实践意义和研究价值。本文在深入研究HSI彩色空间的基础上,结合两种不同的RGB-HSI转换算法,在硬件上达到RGB-HSI高精度的转换与还原。结合并行排序算法和快速中值滤波算法,在减少硬件资源消耗的同时,完成对7×7窗口内元素的快速排序。该系统在硬件资源、精度和速度等方面满足FPGA的设计理念,可广泛应用于光学条纹图像的相位分析、智能监控等领域。
