基于荷载试验的自锚式悬索桥有限元模型修正
2022-08-02欧代军李传友
欧代军,李传友
(1.浙江鼎盛交通建设有限公司,浙江 绍兴 312000;2.中交二航局第四工程有限公司,安徽 芜湖 241000)
目前,结构有限元模型修正已经成为许多学者研究的热点。外国学者Snanyei等基于静载试验对某钢结构模型进行修正;任伟新采用响应面法对桥梁结构进行有限元模型修正,该方法可以显著提高修正效率;邓苗毅等基于静载试验对五跨连续箱梁桥进行有限元模型修正,修正后的模型更真实反应桥梁结构受力状态;方志等基于静动载试验对斜拉桥有限元模型修正。本文基于动载试验测前6 阶自振频率,采取灵敏度分析对有限元模型修正,同时静载试验结果与修正后的模型相吻合,表明该方法的正确性,可以为该桥型今后运营状态评估提供参考。
1 脉动试验方案
某自锚式悬索桥跨径布置为(30+60+150+60+30)m,主梁采用叠合梁,主梁悬吊部分钢梁全长270m,桥面板全宽为25.5m。两根大缆间距28.5m,矢跨比为1/5.5,主缆采用预制平行钢丝索股,每根主缆由19 股索股组成,每股由127 根直径5mm 镀锌高强钢丝组成。全桥吊索共46 对,92 根吊索。主塔采用门型,塔顶处主缆IP 点高程为45.614m,主塔位于水中,均采用分离式基础。
脉动试验选择夜间安静、外界环境干扰小的条件下进行,测试断面及测点布置见图1,脉动试验采用无线模态测试系统,模态分析得到桥梁结构的自振特性参数。
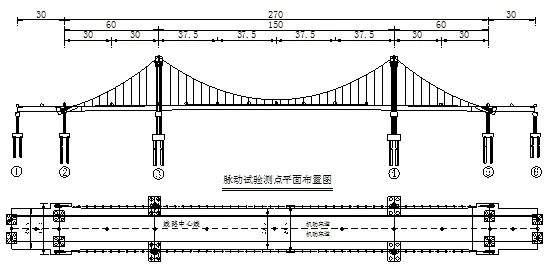
图1 脉动试验测试断面与测点布置(单位:m)
2 自锚式悬索桥有限元模型的建立
2.1 初始有限元模型
采用Midas/Civil 建立某自锚式悬索桥有限元模型,计算模型采用单梁模式,主缆简化为多段悬链线单元,全桥共398 个节点,375 个单元。主梁、塔柱、桥墩均采用梁单元,主缆和吊索采用索单元模拟。主缆和塔顶刚性连接,加劲梁约束按实际支座布置考虑,主梁和吊点刚性连接处理,塔底固结考虑。图2为有限元模型图,表1为设计参数初始值。

图2 某自锚式悬索桥有限元模型图

表1 设计参数初始值
2.2 初始有限元模型计算结果
脉动试验计算结果与有限元计算比较见下表2。可看出,实测自振频率均大于有限元计算值,表明建模时结构刚度比实际值偏小,且前六阶振型均是主梁振动。
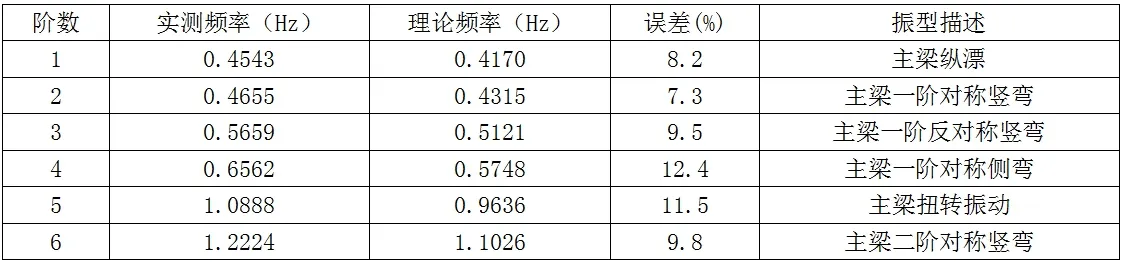
表2 脉动试验与理论计算频率对比
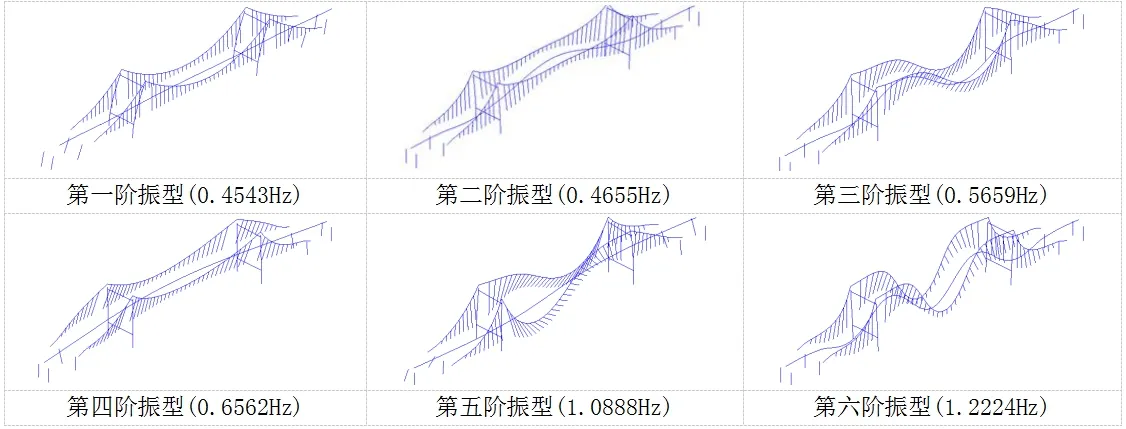
图3 某自锚式悬索桥前六阶实测振型
3 构造目标函数以及灵敏度分析
3.1 目标函数构造
本文根据脉动试验结果,构造符合实际情况的目标函数:
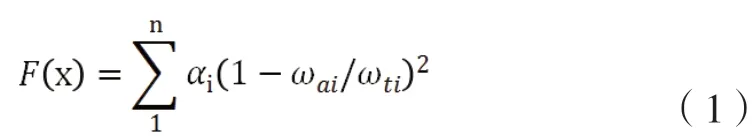
3.2 设计参数灵敏度分析
选择出灵敏度高的参数进行修正,使实测值与模型计算更吻合。本文借助Matlab 中优化梯度法对桥面铺装厚度、主缆弹模、主缆泊松比、主梁Q345 弹性模量、主梁Q345 泊松比、主梁Q345 密度这些参数进行灵敏度分析。当设计参数变化±1%时,目标函数对设计参数灵敏度见下图4。
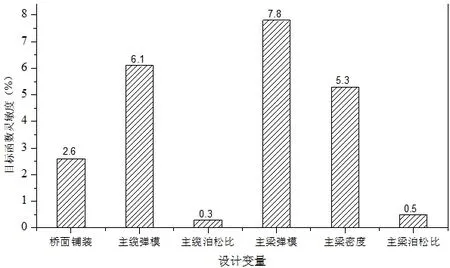
图4 目标函数对设计参数灵敏度
目标函数对设计参数灵敏度为:

从图4看出,主梁弹模、主缆弹模、主梁密度、桥面铺装四种因素对频率计算结果影响很大,作为待修正参数,而主梁及主缆泊松比对频率计算影响很小,不再考虑这两个参数影响。
4 修正后模型计算结果
对上述参数进行修正,采取子空间迭代法对修正后模型进行模态分析,设计参数修正前后比较见表3,计算结果见下表4。

表3 设计参数修正前后比较
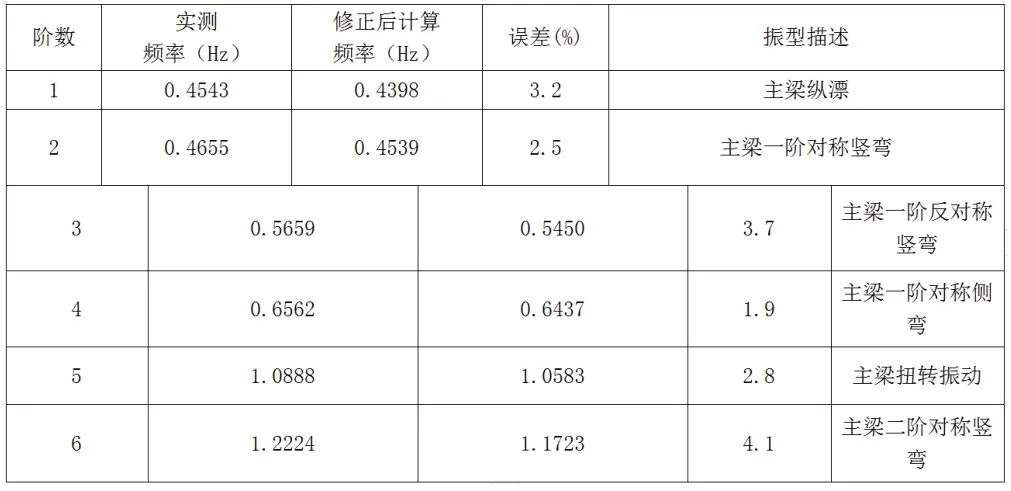
表4 脉动试验实测频率与修正后模型计算值比较
从表3看出,对主梁弹模、主缆弹模、主梁密度、桥面铺装四种设计参数修正偏差在7.3%~19.5%,从表4看出,修正模型后实测频率与理论频率计算值总体误差在10%以内,振型描述是一致的,表明修正后模型的可靠性与该方法的可行性。
5 实桥静载试验结果与修正后的模型计算结果比较
按实桥静载试验加载工况施加在修正后的模型中,限于篇幅下面仅对工况一下主梁挠度情况进行比较分析。
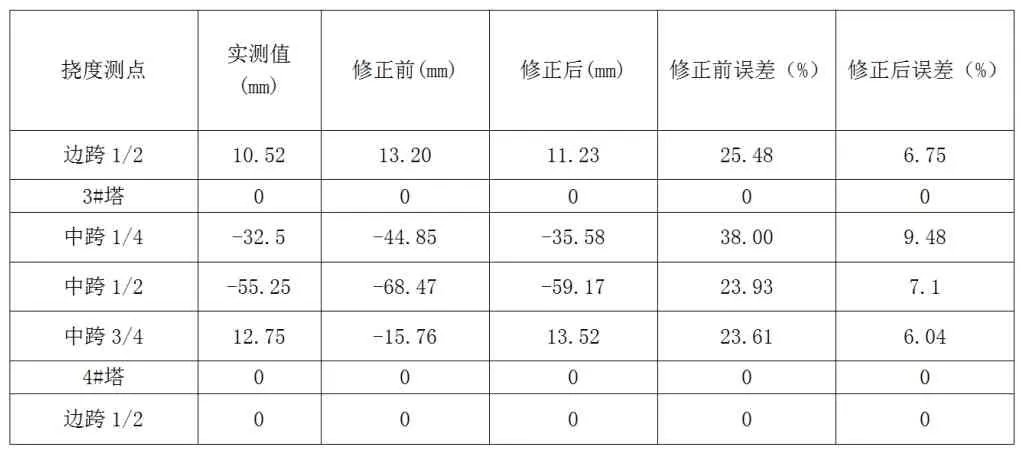
表5 工况一主梁挠度实测与修正后模型计算值比较
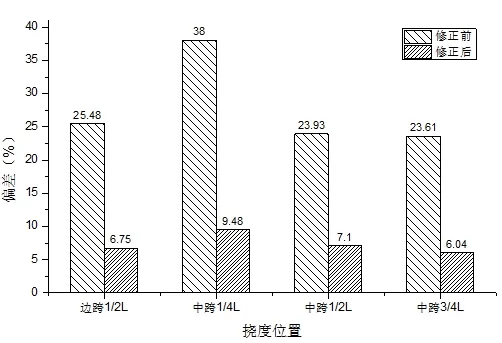
图5 主梁挠度模型修正前、后偏差比较
静载试验工况一下主梁实测挠度值与修正后模型计算值误差在10%以内,表明修正后模型的可靠性与该方法的可行性。
6 结论
本文基于动载试验结果对叠合梁自锚式悬索桥有限元模型进行修正,以前六阶实测自振频率为基准进行设计参数灵敏度修正,并通过实桥静载试验验证修正后的模型的正确性。本文主要得出下面结论:
(1)自锚式悬索桥有限元模型修正灵敏度较高的设计参数主要有桥面铺装、主缆弹性模量、主梁弹性模量、主梁密度等关键因素。
(2)基于动载试验修正自锚式悬索桥有限元模型的方法是可行的,通过实测前六阶振型频率作为修正的出发点,修正灵敏度高的设计参数,使修正后模型计算频率与实测振型频率偏差在10%以内,吻合度较高。
(3)通过实桥静载试验,主梁实测挠度值与修正后模型计算值误差在10%以内,表明修正后模型的可靠性与该方法的可行性。

