桥梁施工缆索吊装系统地锚单桩数值模拟与分析

2022-08-02肖正恩周海发王寿武朱莎莎

中国水运 2022年6期

肖正恩，周海发，王寿武，朱莎莎

（1．云南云桥建设股份有限公司，云南昆明 650101;2．昆明理工大学，云南昆明 650051；）

桥梁施工缆索吊装系统的桩式地锚施工简单，效果明显，但其稳定性易受周围土体性质影响。桩式地锚在受力时有竖直方向和水平方向运动趋势，在竖直方向上的受力作用类似于抗拔桩，受上拔荷载的影响，在水平方向上的受水平拉力的影响。目前，国内对于桩式地锚的受力变形计算大多借鉴抗压桩的理论，且由于群桩效应的存在，在理论验证时大多采取验证单桩的方法。随着计算机程序的快速发展，各种数值模拟软件被大量开发并投入应用，使得实际工程可以通过模型的形式比较形象地展现在设计者面前。林峰对桩式地锚的设计理论和施工流程做了介绍，说明了桩式地锚在桥梁的缆索吊装中的适用性和优越性；姜成潼利用理论计算和数值模拟方法对某边坡工程采取的桩锚-框锚支护结构的受力机理进行研究，将得到的桩顶水平位移值与一般支护结构对比，证明了桩锚-框锚支护结构能够更好地平衡剩余边坡滑力。本文在前人研究的基础之上，基于实际工程背景，运用理论计算和数值模拟相结合的方法对某斜拉桥施工缆索吊装系统地锚施工方案中的单桩进行稳定性进行验证，并分别改变单桩的桩长、桩径和拉索角度，分析单桩因素改变对桩身位移的影响。

1 工程背景

1.1 工程概况

斜拉桥项目位于云南省某高速公路上，全程1330米，主桥为双塔三跨钢箱斜拉桥。施工缆索吊装系统布置如图1所示。根据钻孔勘探资料可知土层大致分为三种，根据粒径和含量多少可知研究点土层岩性多属于漂石粒组和卵石粒组的巨粒土，还有部分粗粒组即细砂，因此认为力学性质主要按照碎石土分类，具体分层参数见表1。

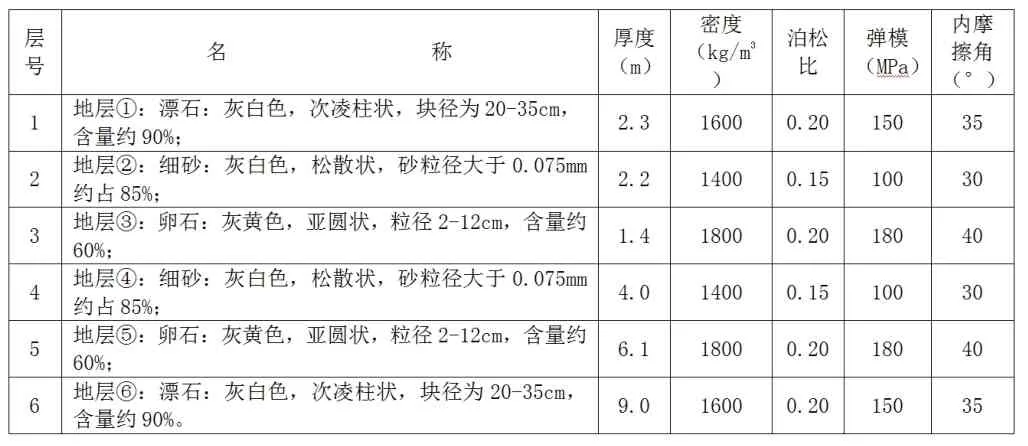
表1 土层参数

图1 缆索吊装系统布置图

1.2 桥梁施工缆索吊装系统地锚施工方案

桥梁施工缆索吊装系统地锚采用桩式地锚，桩长16m，桩径2.0m，共9 根，梅花型双排桩布置，采用C30 钢筋混凝土钻孔灌注桩。群桩桩顶设置C30 混凝土承台，承台尺寸25×10×2m。布置如图2所示。

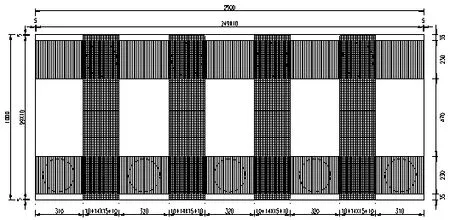
图2 桩式地锚布置图（cm）

2 单桩数值模拟分析

2.1 基本假定和模型

基本假定和模型如下：①忽略水流对土体开挖的影响，不考虑土体流失对桩土体产生的影响；②岩土体为均匀地质；③群桩桩顶与承台刚性连接；④假设9 根桩平均受拉；⑤土体模型采取圆柱形隧道外围渐变网格（radcylinder），本构关系为莫尔库伦；桩体建模采用柱体网格（cylinder），本构关系为弹性。桩土之间的相互作用采取接触面（interface）来模拟受力。以桩心为原点在FLAC 3D 中建立以x、y、z 三轴为方向的坐标系，x 轴向右为正，z 轴向下为负，按照地层厚度建立三维模型。有限差分计算域为8m×8m×27m。

2.2 模拟结果分析

图3是单桩受极限拉力作用下在水平方向产生的桩土位移云图。图4是隐藏土层，只显示单桩水平位移的模拟图。从图中可知受极限拉力后，单桩在靠近桩顶附近的区域产生较大的水平位移值，最大数值为5.05mm，在接近桩底附近的范围，水平位移值较小，平均水平位移值为2.8mm。随着桩深的增加，水平位移值逐渐减小，可知来自上部的荷载从桩顶到桩底再到土层达到了较好的传递受力效果。根据规范中允许敏感性桩身的最大水平位移小于或等于6mm 时桩身不开裂，说明模拟结果相对安全。

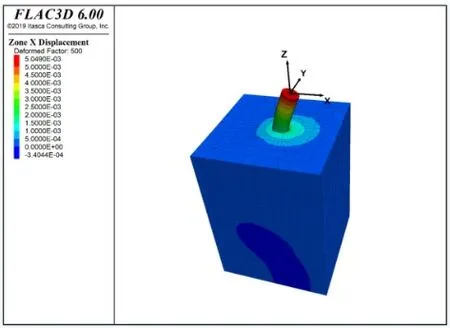
图3 放大桩土水平位移效果图

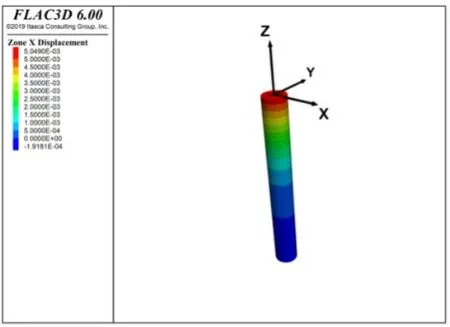
图4 单桩模拟水平位移云图

3 水平位移理论计算与分析

已知最大拉力合力T=11048.285KN，则水平推力，竖直上拔力。地基比例系数m 取常数为20000KN/m4 ，则桩身计算宽度和变形系数为：

式中：k 为基础形状的换算系数，kf 为平面工作条件的系数，EI为桩身抗弯刚度，由于α×h=4.96＞2.5，故按照弹性桩计算。

将水平拉力平均分配给9 根桩基，桩头弯矩M是水平拉力的0.3 倍，Ax 表示单位水平力产生的桩顶水平位移，B表示单位弯矩产生的桩顶水平位移，根据弹性桩规定查表可得数值，最终得到桩顶x轴向位移：

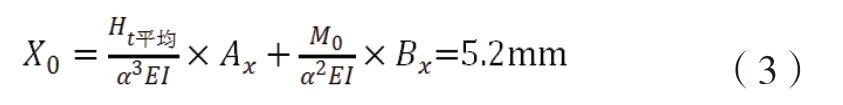
数值模拟得到的最大水平位移值为5.05mm，而理论计算结果为5.2mm，都在规范的安全范围内且两者的误差仅约为2.88%。存在的误差是因为数值模拟在程序计算中将更多的地质参数代入了计算，所以使得计算结果偏小。

4 不同工况下桩身最大水平位移分析

为研究单桩在受极限荷载作用下桩长、桩径和拉力角度分别改变对单桩水平位移产生的影响，将模拟不同工况下单桩桩身位移并对这些具体的数值进行分析对比。分三种工况：①桩径、拉力角度不变，改变桩长；②桩长、拉力角度不变，改变桩径；③桩长、桩径不变，改变拉力角度。

在FLAC 3D 中监测不同工况下桩身受拉产生的最大水平位移，三种工况的监测数据如图5、图6、图7所示。

图5 不同桩长最大水平位移值监测图

图6 不同桩径最大水平位移值监测图

图7 不同拉力角度最大水平位移值监测图

（1）从图5可知，在改变桩长，不改变其他条件的情况下，桩长以12m 为初始值，每隔1m 递增，直到19m 结束，发现桩身最大水平位移值随桩长增加而减小且均小于6mm 并在5mm 左右上下浮动，桩长在12～19m 之间，桩身未产生开裂现象，单桩处于较稳定状态。

（2）在改变桩径，不改变其他条件的前提下，桩径以1.5m 为起始值，按照0.05m、0.15m、0.25m 或者0.5m不定值增加，以3m 为结束值，从图6可知随着桩径逐渐增大，最大桩身水平位移值逐渐减小，两者呈负相关关系。桩径为1.5m 和1.75m 时，最大桩身水平位移值超过了6mm，按规范判断，该单桩有可能会发生桩身开裂现象，此时的两个桩径值不能被作为桩径设计值，桩径值在1.90～3.0m 之间，最大水平位移值在规定的安全区间，可以被作为设计值选取使用，考虑到施工成本的问题，尽可能在保证安全的前提下选择较小桩径值。

（3）从图7可知，在改变拉力与单桩倾角，不改变其他条件时，拉力角度与最大桩身水平位移的关系近似成直线型下降趋势，可见适当增大拉力角度能够有效较小桩身的水平位移，但是限于施工现场拉索布置要求以及其他结构的布置，拉力角度不能够自由变化，所以可在限制条件下尽量使拉力角度大一点。