基于蒙特卡洛方法的船闸通航条件限制模型

李 坦

(广西壮族自治区交通运输厅，广西 南宁 530012)

0 引言

随着科技进步，船舶日益大型化，向着大吨位、大尺度的方向发展，其实际吃水深度与航道通行标准的矛盾日益凸显，如何科学地制定相关规定，才能最大限度地利用现有航道的航运基础设施通行能力，是目前的关注焦点。

在西部交通建设科技项目“三峡船闸过闸船舶吃水控制标准关键技术研究”中，采用了基于实船试验的方法对三峡船闸过闸船舶吃水控制标准进行了系统研究，其成功经验为船闸通航限制条件的采集提供了参考与借鉴。

王伟等[1]使用蒙特卡洛方法与二维装箱启发式算法相结合的随机仿真算法，对不同尺度船闸设计方案的通过能力进行了计算，并对结果进行讨论，得出了切实可行的优化方案。有学者在对开普敦港进港航道的设计深度验算中，使用了蒙特卡洛方法，并将swan模型应用于波浪处理中，同时在船舶对波浪的响应这方面选取了简化的经验公式，但是没有考虑到船舶在波浪中的横倾和纵倾问题。而Gucma等[2]虽然使用了类似的方法，但是更偏向于经验型，使用了建模与实船实验相结合的方式，考虑了误差影响，计算得出了搁浅概率，却受限于试验次数和条件设置，误差等参数的选取进行了大量的简化。吴礼国等[3]通过整体模型和船模试验，采集了船闸引航道口门区的通航条件，验证了船闸设计方案的合理性和可行性。

1 船闸通航限制条件模型

为解决船舶实际吃水深度与航道通行标准的矛盾，可采用实船试验的方式，通过多次航行、多次试验的方式来对船闸过闸船舶吃水控制标准进行研究。也可通过建立相关模型，并采集船舶的相关参数和航道的相关参数，利用采集到的参数对船舶通过船闸时的航行情况进行仿真并评估，进而得到限制船舶通过的相关条件，最终可根据限制条件来确定新的航行规则。本文在此主要介绍第二种方法中基于蒙特卡洛方法的船闸通航限制条件模型。

1.1 蒙特卡洛仿真

蒙特卡洛方法是用事件发生的频率决定事件发生的概率，又称“计算机随机模拟法”，是一种基于“随机数”的计算方法。基于蒙特卡洛思想，分析研究的方法就可以变得很轻松，从某种程度来说，可以诠释蒙特卡洛方法相对于数值方法的优越性。

1.2 船闸通航限制条件模型

1.2.1 基于实船试验的船闸通航条件模型的建立

西部交通建设科技项目“三峡船闸过闸船舶吃水控制标准关键技术研究”[4]中，对三峡船闸过闸船舶吃水控制标准进行了系统研究。研究中指出，过闸船舶吃水控制标准直接取决于船舶综合航行下沉量和不触底富裕水深的大小。船舶综合航行下沉量由船舶航行下沉量、推移波、非恒定流引起的水位波动及船舶纵倾等四部分组成：

D=L+ΔD+a

(1)

a=as+ΔDw+aw+t

(2)

式中：D——闸室门槛水深；

L——允许过闸船舶的最大吃水；

as——船舶实际下沉量；

aw——推移波;

我相信随着对混合式教学模式的深入研究和使用，它巨大的网络平台优势一定会得到更充分的利用，收到更好的教学效果。

ΔDw——非恒定流引起的水面波动；

ΔD——安全富裕；

t——船舶纵倾。

1.2.2 船闸通航限制条件模型参数的选取

根据上文所述，可得出影响船闸通航条件的参数如下：

(1)闸室有效尺度。闸室指的是船舶在过闸时所处的“空间”。闸室的有效尺度会影响闸室内船舶的吃水、下沉量、纵倾以及不触底的安全水深和推移波的大小等。

(2)船舶满载吃水。船舶满载吃水指的是船舶在正常航行状态下能允许的最大吃水，同时也是船舶在满载排水量状态时的吃水。

(3)船舶纵倾。纵倾是指船舶自正浮位置向船尾或船首方向倾斜的一种浮态，其大小用纵倾角表示，是纵倾后中横剖面与铅垂平面的交角。由于本文的研究对象为内河运输船，结合几位专家意见后，将操作纵倾设为3°。如图1 所示。

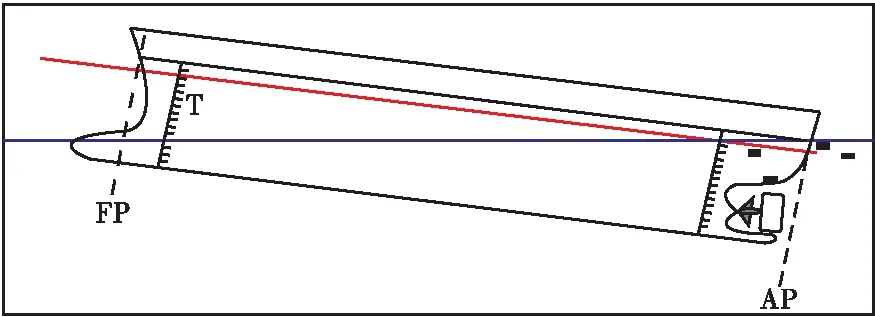
图1 船舶纵倾示意图

(4)船舶航行下沉量。船体在浅水中的航行下沉量，主要包括船体整体下沉和纵倾变化两部分。一般来说船舶的航行下沉量可以采用BarassⅡ公式：

(3)

(4)

Cb——船舶方形系数；

AS-vertical——船体横切面面积(m2)；

Ach——船闸室内横切面面积(m2)；

VK——船舶的对地航速(km/h)。

根据式(3)、式(4)，求取船舶航行下沉量的关键在于船舶的航速。航速由测量船舶进出各船闸时的实际情况得出，求取其平均速度，得到进闸船舶均值为0.1，标准差为0.2的正态分布。

(5)不触底的安全富裕水深。富裕水深是指设计船舶在标准载重静浮状态时，船底龙骨下至航道底的最小距离。国内还没有一个统一的富裕水深标准，因此本文考虑了前文中提到的《三峡船闸过闸船舶吃水控制标准关键技术研究》中的相关结论：当门槛水深分别为5 m、5.5 m、6 m时，船舶富裕水深分别为1.1 m、1.2 m、1.5 m。

除上述五种参数外，应另考虑实际门槛水深的问题。

根据设计门槛水深、实际门槛水深、实际水位、设计最低通航水位的水位值之间的关系，可得到：实际门槛水深=设计门槛水深+(实际水位-设计最低通航水位)。

2 实例验证

本文选择广西西江干线船闸进行验证。根据前文中所述的船闸通航限制条件中“安全富裕水深”的相关经验，在考虑西江干线船闸的实际情况与通航船只的吨位情况后，船闸不触底的安全富裕水深取0.3 m。

2.1 西江干线船闸通航条件概述

2.1.1 船闸通航水位和门槛水深

西江干线的船闸有：长洲船闸(一、二、三、四线)、贵港航运枢纽船闸、邕宁船闸、桂平航运枢纽船闸(一、二线)和西津船闸。

对于船闸的设计来说，船闸的上下游设计最高和最低通航水位、门槛水深是船闸设计最为关键的内容。不同吃水的船只通过船闸时需要根据具体船闸实际的水位和门槛水深进行判断(表1)。

表1 船闸的通航水位和门槛水深一览表

2.1.2 船闸实际最高与最低通航水位

分别统计2020年每月船闸最高通航水位与最低通航水位，结果如图2所示。

图2 西江干线船闸最高与最低通航水位统计柱状图

2.2 西江干线流域船舶通航流量统计分析

船舶通航条件沿干线航道条件会发生变化，但总体较好。最大过闸船舶参数如下页表2所示。

表2 2020年西江干线过闸船舶最大吃水参数表

2.3 西江干线船闸仿真结果

本文选择邕宁船闸于船舶最大吃水情况下的仿真结果进行展示，其结果与实际情况相比较，最大吃水相差均<15%，如图3所示，进一步印证了仿真实验的可行性。继续对广西西江干线各船闸进行验证，抽取西江干线各船闸仿真结果中最大船舶吃水情况进行展示，说明本研究中使用的方法是科学合理的。仿真结果如表3所示。

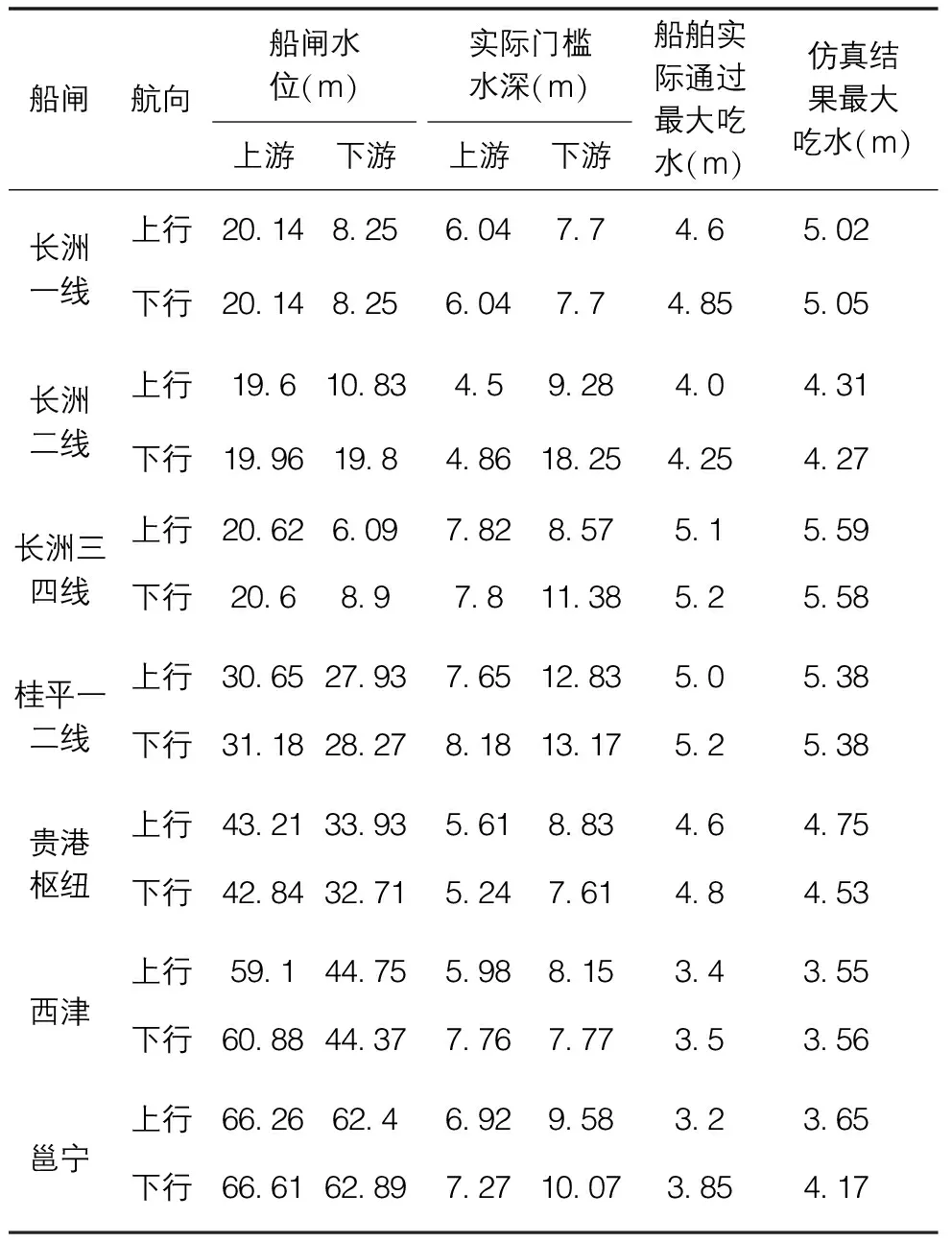
表3 西江干线各船闸最大船舶吃水情况下仿真结果表

图3 邕宁船闸仿真结果与实际结果差值柱状曲线图

3 结语

本文介绍了蒙特卡洛方法的基本思想和在船舶航行领域的应用，并分析了影响船舶吃水的各个因素及计算的取值区间；对各个船闸最大船舶吃水工况下进行仿真模拟，将得到的仿真结果和实际情况进行对比，得出了仿真能通过的最大船舶吃水与实际通过的最大吃水相差不大的结果，且符合实际航行情况的结论，证明了蒙特卡洛方法的有效性。