Anderson localization of a spin–orbit coupled Bose–Einstein condensate in disorder potential

Huan Zhang(张欢)， Sheng Liu(刘胜)， and Yongsheng Zhang(张永生)

CAS Key Laboratory of Quantum Information，University of Science and Technology of China，Hefei 230026，China

Keywords: Bose–Einstein condensates，Anderson localization，spin–orbit coupling

1. Introduction

It has been over sixty years since Anderson’s prediction of electrons’localization in metal lattice sites with disorder.[1]The mechanism of this metal–insulator transition is different from the Mott transition，[2]in which the electron–electron interaction plays an essential role.Anderson found that different eigenstates of non-interacting electron in lattice sites are scattered by disorder and interfere destructively with each other，which results in absence of diffusion in the strong disorder limit. In the one or two-dimensional (2D) case， the Anderson localization appears even in the sufficient weak disorder，[3]except some correlated disorders.[4]However，in the 3D case，there is a mobility edge separating localized and non-localized quantum states. The phenomenon of Anderson localization is universal and has been observed indirectly on solid state of wires， films and bulk systems，[5，6]or directly on ultra cold atom platforms[7，8]and photonic lattices，[9，10]etc. Spin–orbit(SO)coupling is relativistic effect of the moving electron. As a result， in condensed matter physics， the transport of electrons in materials becomes spin dependent， which affects the Anderson localization.[11，12]

An ultra-cold atom system is a fascinating way to study the condense matter problems[13]owing to its unprecedented control of system’s parameters and its ability to mimic the condensed matter system. Anderson transition of attractive fermions are investigated theoretically mainly on lattice systems.[14–16]Bose–Einstein condensate (BEC) provides a promising platform in the study of bosons’ Anderson localization. One-dimensional interacting BEC expanding in correlated disorder can exhibit Anderson localization.[17–19]In the long expanding time limit， the length of Anderson localization of a BEC continues to increase with the time evolving in the presence of the repulsive interaction.[20]Several experimental studies directly observed the Anderson localization in BECs.[7，8]The realization of SO coupled BECs in ultra cold atom system sheds new light on studies of superfluid and condensed matter physics.[21，22]It has made significant progress and advanced rapidly in recent years. By tuning the parameter of SO coupled cold atom gas using Feshbach resonance， one can reach the regions of topological insulators or superconductors.[23]The SO coupling plays an crucial effect on Anderson localization of BEC in 1D or 2D systems.In a 1D quasi-periodic optical lattice， SO coupling induces an intermediate phase mixing extending state and localizing state.[24]Also， the SO coupling and Rabi coupling favors the localization or delocalization of the BEC depending on the phase difference between the two components.[25]In a 2D bichromatic optical lattice，SO coupling favors localization，whereas Rabi coupling has a slight delocalization effect.[26]The spin of SO coupled BEC manifests the precessional and anomalous evolution in the disorder potential.[27]In a 2D disorder system，interference between the Rashba and the Dresselhauss SO coupling leads to a strong dependence on the system’s mobility edge which will reach infinity when equally mixing two kinds of coupling.[28]The expansion of a 2D BEC along the direction of SO coupling can be greatly slowed down due to the diverge of its effective mass near the critical point of phase transition without the presence of disorder.[29]In Raman induced SO coupled BEC，by adjusting the Raman coupling frequency，one can reach different phases，like zero-momentum phase or magnetic phase， of SO coupled BEC. Especially in magnetic phase，the system can simulates an electron transporting under the effect of magnetic field. The non-equilibrium dynamics of BEC in these phases with disorder potential remains unexplored.

In this article，in contrast with Ref.[28]，we focus on the effect of SO coupling on the Anderson localization in different phases following the method of Ref.[20]. We investigate the non-equilibrium dynamics of an SO coupled BEC expanding under a speckle disorder by numerically solving the 1D Gross–Pitaevskii equation. The 1D simulation corresponds to the following experiment: Initially，the87Rb cold atom gas is confined in the cigar-shape trap and a homogeneous magnetic bias field is applied along thexdirection. The incident two Raman lasers act on the atoms atπ/4 and 3π/4 with thexdirection to synthesize the Rashba[30]and the Dresselhaus[31]SO coupling interactions with equal contributions.[32]Then the harmonic potential is abruptly released in longitudinal direction and the condensate expands under the speckle disorder located in the same direction. We study the evolution of three different phases of SO coupled BEC in disorder environment. In the single-minimum phase，i.e.，the zero-momentum phase， the BEC exhibits Anderson localization with a larger localization length than normal BEC and the SO coupled BEC in magnetic phase. In the magnetic phase and stripe phase，we find that the SO coupled BEC will exhibit non-monotonical increase of localization length with the fitting interval becoming larger. Specially， the SO coupled BEC will experience spin relaxation in magnetic phase. In Section 2， we describe the system model under consideration and the numerical method we used thoroughly. In Section 3，we show our numerical results in different system phases and analyze the results based on the localization theories. The conclusion is presented in Section 4.

2. The system model and numerical method

The Hamiltonian of the system can be expressed as[32]withωx=50×2πHz being the longitudinal frequency of the trap andVd(x)denoting the speckle disorder. The strength of SO coupling is

where

withkinandλ= 782 nm being the wave vector and the wavelength of the incident light， respectively. The 1D timedependent Gross–Pitaevskii equation reads

ForΩ ≥Ωc，the system locates in the zero-momentum phase.There is only one minimum of ground state energy， wherekx=0.

If the interaction coefficients are notSU(2)invariant，i.e.，g12／=g11=g22=g， the ground state of mean field Hamiltonian(1)can be in stripe phase. The ground state is the superposition of two degenerate ground states of SO coupled BEC in the plane-wave phase. If|g12-g|≪1， the corresponding minimum of ground state energy in plane-wave phase can be reached when[33]

whereσDis the correlation length of the disorder， we setV0=0.3[Eint(t=0)+Ekin(t=0)] to match the weak disorder condition and useσD=5x0throughout our simulation.

The Hamiltonian can be split into kinetic part and nonkinetic part. The time evolution of the kinetic part can be efficiently calculated through Fourier transformation. We prepared the ground state of the BEC by imaginary-time evolution using the Strang-splitting method in a box [-L，L] with 214×100 grid points， whereL= 2.4×104x0. Then we evolved the wave function using higher-order operator splitting method[35]and used the adaptive time step similarly to Ref. [20]. The tolerance is set to be 10-10to reach the converge results.

We numerically calculate the disorder-averaged particle density of the two spin components and their sum in real space and quasi-momentum space，

We also calculate the evolution of the mean width

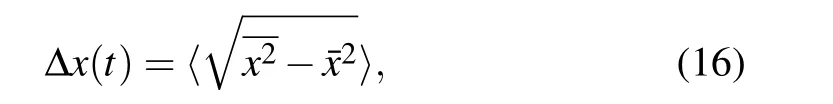
and spin unbalance〈σz〉， where the brackets mean disorderaveraged and the bar means being averaged over the state.The curves ofn(x，t)andn(k，t)are smoothed with Gaussian filter of width 6x0and 0.1/x0，respectively. Our main results will be presented in the next section. The evolution time of the most results is set to be 100t0，which reaches the time scale limit of the present experiments.

3. Localization in different phases

Whent ＜0， we prepare the system in the ground state with different strengths of Raman coupling. Whent ＞0， we switch off the confined potential in longitudinal direction and switch on the speckle disorder at the same time. We never change the strength of interaction throughout the simulation，which is close to the real experiment.

3.1. Zero-momentum phase

We plot the density of two components of SO coupled BEC att=100t0in Fig.1. We can see the apparent asymmetry of density distribution of two components.This asymmetry only has minor effect and is hard to be observed in the experiment.

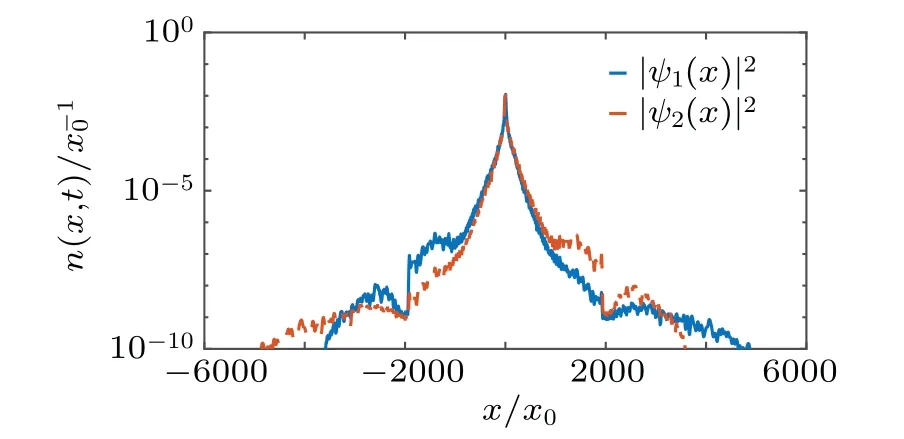
Fig. 1. Real-space distributions of density of two components of the SO coupled BEC in zero-momentum phase at time t=100t0. The densities are averaged over 20 speckle disorders. The strength of Raman coupling Ω =1.5Ωc.

In order to compare the localization properties of SO coupled BEC in zero-momentum phase and two-component normal BEC without SO coupling，we plot the density distribution of two kinds of BEC at different times in Fig.2.It is found that the width of the central density with SO coupling is slightly larger than that of the normal BEC att=100t0. Then we assume that the densityn(x，t)=|Ψ(x，t)|2displays exponential shape in some local regions，

whereC(x)is the fitting parameter dependent on the location of intervals，Llocis the localization length of the BEC. The results are presented in Fig. 3. We can see from Fig. 3(a)that the localization lengthLlocof SO coupling BEC is larger than that of normal two-component BEC when the fitting interval is large (x ＞500x0). Furthermore， in the region close to the center of BEC， the localization lengthLlocof normal two-component BEC is slightly larger. In Fig. 3(b) we plot the fitting error，which is smaller compared to the localization length.

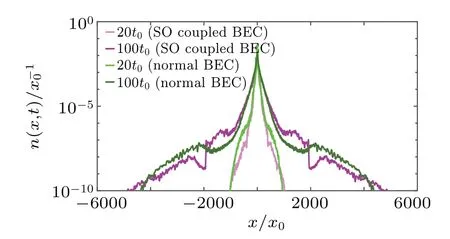
Fig.2. Real-space distributions of density of the two-component BEC with or without SO coupling at times t =20t0 and t =100t0 under the same conditions. The densities are averaged over 20 speckle disorders.

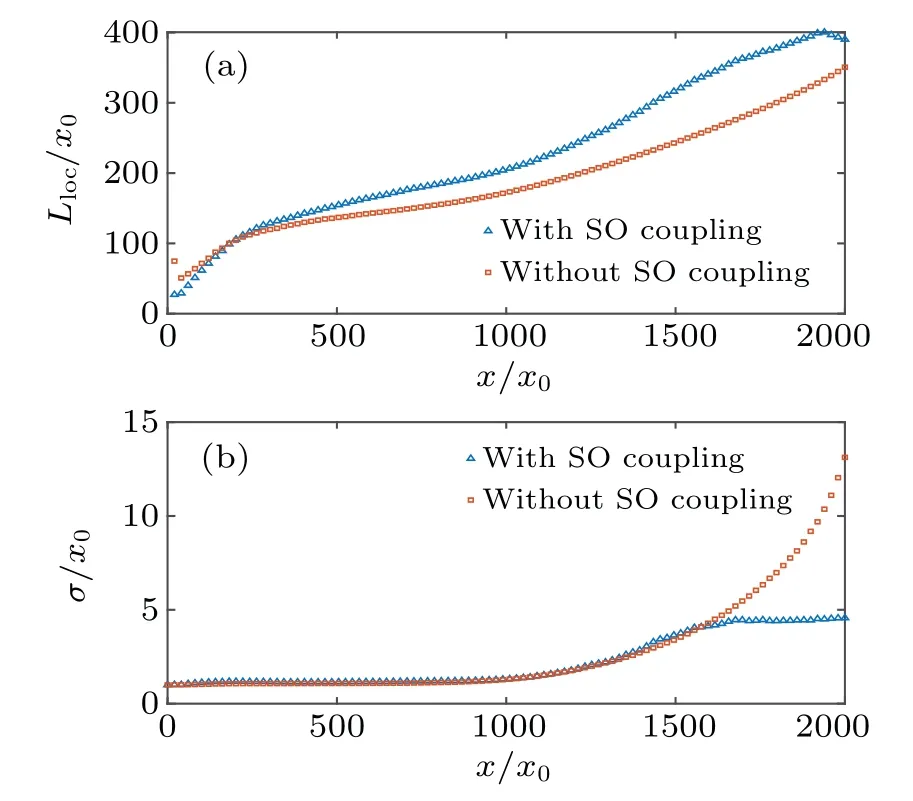
Fig. 3. (a) Localization length Lloc of the SO coupling BEC in zeromomentum phases and normal two-component BEC with same strength of Raman coupling by fitting the real-space densities at t =100t0 to Eq.(17). (b)Standard deviation of linear fitting in two kinds of BEC.

We also plot Δx(t)with time evolving in Fig.4. It can be clearly seen that the average width of the real-space distribution of density with SO coupling is smaller than that without SO coupling at the beginning. The reason is that the expansion of the SO coupled BEC of zero-momentum phase in the SO coupling direction is much slower than that of the normal BEC owing to its larger effective mass，[29]although this energy conversion process in disorder is much slower than the free expansion of the SO coupled BEC. We can expand the dispersion relation near the minimum and obtain the effective mass in the direction of SO coupling as

WhenΩ=1.5Ωc，the effective massm*=3m ＞m. Without the disorder，the larger effective mass will make the expansion slow down in the SO coupling direction. With the disorder，the SO coupled BEC will manifest slower expanding at the beginning， but it will also exhibit Anderson localization later and has a close localization length with the normal BEC. As we can see，the shaded areas in Fig.4 overlap with each other att=100t0. The expanding effect is governed by the quasiballistic expansion of the rapidly moving extended state and the delocalization effect of SO coupling，which will both make the BEC expand continuously.

Fig. 4. Time dependence of mean width Δx of density distribution of normal spinor BEC and SO coupled BEC in zero-momentum phase.The colored shaded area around each curve represents one standard deviation from average width resulting from 20 realizations of speckle disorder.

3.2. Magnetic phase

We setΩ=0.5Ωcand prepare the SO coupled BEC in the ground state， whose real-space distributions of density of two spinor components are presented in Fig.5.

Fig. 5. The ground state density distributions of two components of the SO coupled BEC in the magnetic phase. The strength of Raman coupling Ω =0.5Ωc.

It can be seen that〈σz〉／=0 for the magnetic phase in contrast with the spin-balanced state in zero-momentum phase，which indicates that theZ2symmetry is broken in the magnetic phase. We let the BEC expand in speckle disorder for 100t0. The results are strikingly different from the ones in zero-momentum phase. Att= 100t0，〈σz〉 ≈0， which shows a spin relaxation process in expansion resembling the Dyakonov–Perel mechanism.[36]The spin orientations of particles are random due to the SO coupling. Without the disorder，the expansion of the SO coupled BEC will experience the“self-trapping” in the SO coupled direction when the quasimomentum enters the negative-mass region.[37]We plot〈σz〉as a function of time in Fig.6.

Fig. 6. Behavior of 〈σz〉 of SO coupled BEC in magnetic phase as a function of time with(blue solid line)or without(red dash line)disorder potential.

We find that〈σz〉of SO coupled BEC quickly decreases to nearly zero at aroundt0= 20 in speckle disorder potential. If there is no disorder potential，〈σz〉of SO coupled BEC decreases slower but maintains a finite value 0.6 at aroundt=5t0. The disorder eliminates the“self-trapping”effect and the system enters the spin-balanced state despite the dispersion relation. Figure 7(a)shows higher sharp boundaries and curve wings in both sides of the logarithmic plot，which means that there are different localized regions with different localization lengths. We also plot the quasi momentum distribution of two spinor components in different times in Fig.7(b). The density distributions in quasi-momentum space do not change much in a longer expansion timet=300t0. The enhancement does not appear neark=0 owing to the fact that the quasi momentum of the ground state in magnetic phase is not equal to zero.The absence of Galilean invariance is the particular feature of the SO coupled BEC. There are two kinds of critical velocity in the SO coupled BEC.[38，39]Firstly， the condensate is at rest， and the impurity is moving. There will be excitations in the condensate once the magnitude of velocity reaches some threshold， which is called the the critical dragging velocity.The critical dragging velocity is asymmetric at±xaxis in the magnetic phase and will be decreased to zero in the transition pointΩ=Ωc. Secondly， the impurity is at rest， and the condensate is moving， which is the case in our article. There will also be excitations in the condensate once the magnitude of velocity reaches some threshold，called the critical flowing velocity. The critical flowing velocity is symmetric at±xin both zero-momentum phase and the magnetic phase and will remain finite when crossing the transition point. In the equilibrium ground state，the Hamiltonian in the moving frame of reference is given by[40]

the velocity of condensatevand the quasi-momentum has the following relation(we set¯h=1，vandkare in the same direction):

Fig.7. (a)Real-space distributions of density of two components of the SO coupled BEC in magnetic phase at time t =100t0. (b) Quasi-momentum space distributions of density of the SO coupled BEC in magnetic phase at time t =100t0 and t =300t0. The densities are averaged over 20 speckle disorders. The strength of Raman coupling Ω =0.5Ωc.

We then fit the real-space densities of BEC to Eq.(17)in different intervals. The results are presented in Fig. 8. It can be seen that the localization length of the SO coupled BEC in the magnetic phase will increase non-monotonically as fitting interval becomes larger and has maximum near 1000x0.Moreover，in zero-momentum phase the localization length increases monotonically as the fitting interval increases.We plot the fitting error in Fig.8(b)，which proves the non-monotonical feature of Localization length in magnetic phase. Also，the effective mass of BEC in magnetic phase is 4m/3＞m， while the result in Fig.9 shows that the width of the wave function grows approximately proportional to time and faster than that of normal BEC.The reason is that the ground state of SO coupled BEC in magnetic phase is unbalanced state (〈σz〉／=0)and will experience the spin relaxing process when expanding in speckle disorder，which is a delocalizing process. When the SO coupled BEC has nonzero average spin， the condensate particle will scatter more frequently in the disorder when its spin has to precess under the magnetic field. When the BEC finally becomes localized and spin balanced，it will manifest a larger mean width.

Fig.8. (a)Localization length Lloc of the SO coupled BEC in two different phases and different intervals by fitting the densities at t=100t0 to Eq.(17). (b)Deviation of linear fitting in two different phases.

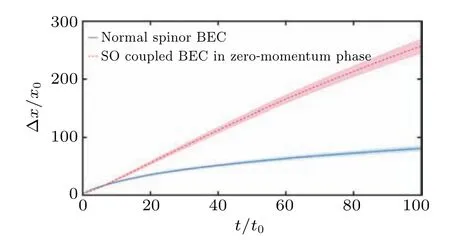
Fig. 9. Time dependence of mean width Δx of density distribution of normal spinor BEC and SO coupled BEC in magnetic phase. The colored shaded area around each curve represents one standard deviation from average width resulting from 20 realizations of speckle disorder.

Fig. 10. The ground state density distributions of two components of the SO coupled BEC in the stripe phase. Ω =0.2Ωc，g12=0.9g.

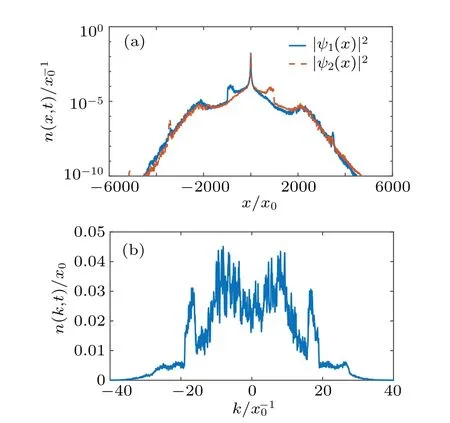
Fig. 11. (a) Real-space distributions of density of two components of the SO coupled BEC in stripe phase at time t = 100t0. (b) Quasimomentum space distributions of density of the SO coupled BEC in stripe phase at time t = 100t0. The densities are averaged over 20 speckle disorders. The strength of Raman coupling Ω =0.2Ωc， the strength of interaction g12=0.9g.

Fig. 12. (a) Localization length Lloc of the SO coupled BEC in magnetic phase and the stripe phase as a function of intervals by fitting the densities at t=100t0 to Eq.(17). (b)Deviation of linear fitting in two different phases.

We fit the real-space densities of BEC to Eq.(17)in different intervals. The results are presented in Fig. 12. The localization length of SO coupled BEC in stripe phase becomes larger than that in magnetic phase but has the same non-monotonical feature. We also plot the time evolution of the mean width in stripe phase and in magnetic phase beforet=100t0in Fig.13. It is obvious that the mean width of SO coupled BEC in stripe phase increases proportionally to time with a higher speed.

Fig. 13. Time dependence of mean width Δx of density distribution of SO coupled BEC in magnetic phase and stripe phase. The colored shaded area around each curve represents one standard deviation from average width resulting from 20 realizations of speckle disorder.

4. Conclusion

In summary，we have investigated the evolution of an 1D SO coupled BEC in the speckle disorder employing the Gross–Pitaevskii equation using the high-order splitting method. The average width of SO coupling BEC in zero-momentum phase is smaller than that of normal BEC at the beginning of expansion due to its larger effective mass. When the system exhibits Anderson localization， the localization length of SO coupled BEC is larger than that of the normal BEC.In magnetic phase，the SO coupled BEC will experience spin-relaxation and exhibit non-monotonically increase of localization length as the fitting interval become larger. The quasi-momentum distribution in magnetic phase shows four peaks owing to the degenerate ground state atk／=0 and the feature of the speckle disorder.The quasi-momentum distributions of the two spinor components are symmetric because of the symmetric critical flowing velocity at±xaxis. In stripe phase，the localizing behavior of the SO coupled BEC is similar with that in magnetic phase but exhibits a larger localization length. Base on the realistic parameters used in our simulation，we expect that the anomaly of localization length can be observed in the future experiment.

Acknowledgements

Y.S.Zhang thanks Professor Chuanwei Zhang for drawing our attention to the topic of Anderson localization of BECs. This work was supported by the National Natural Science Foundation of China(Grant No.92065113)and the National Key R&D Program. The calculation on GPU was performed on the supercomputing system in the Supercomputing Center of University of Science and Technology of China.