基于三元闭包理论的软件回归测试影响域分析方法*
2022-08-01李继秀王月波蒲卿路
刘 涛,李继秀,王月波,蒲卿路,孙 云
(中国西南电子技术研究所,成都610036)
0 引 言
在软件回归测试中,传统方式是将所有测试用例重新执行一遍,当软件系统比较庞大或版本更新比较频繁时,人力成本和测试效率都会受到很大的影响。而回归测试中变更影响分析是重点难点,如何评估测试项更改之后的影响,量化测试项之间的关联紧密程度,避免无关测试用例的执行,是提升回归测试效率的关键。软件回归测试中的影响域分析是回归测试研究趋势,具有研究和应用价值。
三元闭包为社区网络中两个不认识的人提供链路机制。许云峰等人[1]在此算法的基础上实现了社区的划分。孙昊天等人[2]在知识图谱上应用三元闭包知识,更精准地表达了实体之间深层次的关系,更有利于社区网络的研究发展。Liu等人[3]通过三元闭包理论查询蛋白质和模板蛋白质之间的关系,以实现更精准的蛋白质折叠识别。高杨等人[4]在节点相似性上应用三元闭包,并将权重应用于节点相似性指标中,用于提高链路预测的精度。杨梓舒[5]甚至认为三元闭包是驱动社会网络的结构演化的因素之一。若把三元闭包理论用于梳理测试项关系,建立测试项社区网络,寻找定位可能受到影响的测试项,实现测试用例约简的同时,将可能有缺陷概率的测试项纳入回归测试,具备着非常大的实用价值。
自动生成回归测试用例软件系统使用基于三元闭包理论的回归测试影响域分析方法,将软件系统抽象为一个社交网络,软件系统提供的功能抽象为虚拟人,为虚拟人之间定义交流通道类型,通过图论和三元闭包理论构建非直接发生联系的人的关系,给出回归建议。首先建立有向有权图模型,所有系统功能项用矩形表示,关系使用带有方向的箭头表示;再结合三元闭包理论,递归计算每一层三元闭包理论下的推荐值,计算出每个功能项的聚集系数,以及三元关系中可能存在关系的两功能项之间的邻里重叠度;最后是每个功能项推荐系数的算法实现,如果推荐系数大于0.5,则将该功能项纳入回归测试。本文算法实现了测试用例集约简的同时,结合功能项社区网络,针对性地将可能有缺陷的测试用例进行回归测试,提高了影响域分析的科学性和精准性,并已在工程中进行应用。
1 软件系统设计方案
软件系统的组成框图如图1所示。系统输入是获得的测试轮次下所有功能项。基于三元闭包理论的软件回归测试影响域分析方法包括有向有权图模型构建模块、功能项关联概率计算模块、功能项推荐系数计算模块和回归测试用例生成模块四个模块。系统输出是推荐进行回归测试的所有测试用例。
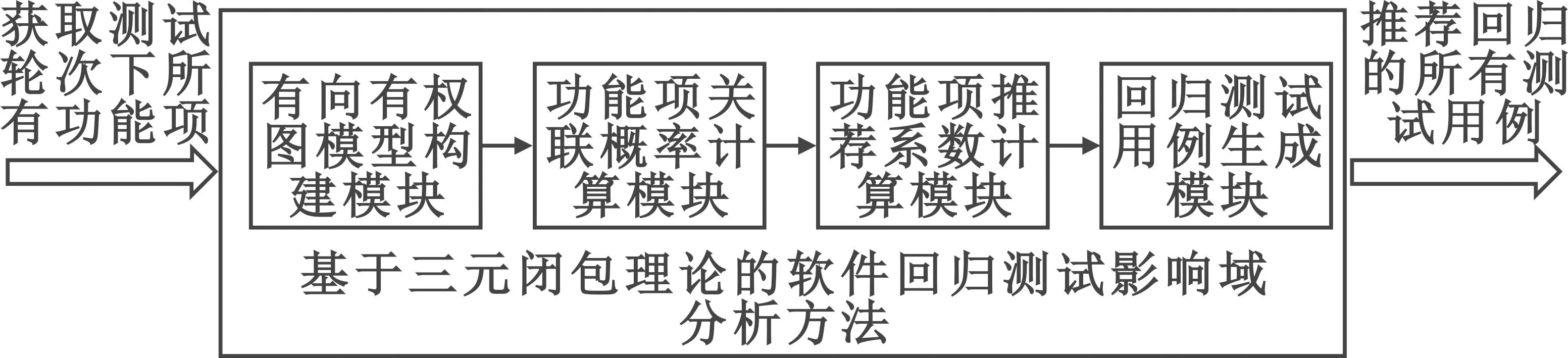
图1 自动生成回归测试用例软件系统组成框图
自动生成回归测试用例软件系统流程图如图2所示。首先获取软件系统测试轮次下所有功能项,判断功能项的通过状态,如果是通过状态,则推荐系数初始化为1,否则推荐系数初始化为0。推荐系数初始化完成后,需要给功能项之间的边关系多个维度值并赋予权值,接着计算功能项聚集系数、邻里重叠度、推荐系数,判断功能项的推荐系数值是否大于0.5,如果大于0.5,则加入回归测试队列,作为回归测试的输入导入到测试需求分析中,流程结束,否则流程直接结束。

图2 自动生成回归测试用例软件系统流程图
2 算法描述
2.1 测试项之间的边关系多个维度赋值并赋予权重
设进行软件回归测试的轮次测试项数量为N,N(i)和N(j)分别表示第i个测试项和第j个测试项,定义(i,j)边描述测试项和测试项之间直接的关系。本文边的权值用Wij来描述,Wij的值介于0和1之间,值越大,说明两者联系更为紧密。文献[6]将社交活跃度与用户信任度等多维度用于社区网络的推荐,受此启发,本文关系定义了多个维度。测试项之间的控制依赖相关性,表示功能项间存在控制与被控制的关系,例如功能项A是生产者,功能项B是消费者,用dc来表示,介于0和1之间,分配权重用wc来表示,值为正整数;测试项之间的数据依赖相关性,表示功能项之间存在共享数据的使用,如全局变量等,用dd来表示,介于0和1之间,分配权重用wd来表示,值为正整数;测试项之间的数据交互相关性,功能项之间有数据交互,例如功能A需要使用功能B处理后的数据,用di来表示,介于0和1之间,分配权重用wi来表示,值为正整数;测试项之间的性能依赖相关性,表示功能项对系统的性能(如计算精度、响应时间、CPU/内存/存储资源等)有影响,用dp来表示,介于0和1之间,分配权重用wp来表示;测试项之间的时序依赖相关性,表示功能项之间执行顺序不同对系统可能造成影响,例如多线程间的同步或互斥等,用dt来表示,介于0和1之间,分配权重用wt来表示;测试项之间的其他依赖相关性,表示在上述依赖关系之外的其他依赖,用do来表示,介于0和1之间,分配权重用wo来表示,值为正整数。相关性数值越大,表示两个测试项之间该项的联系越紧密;依赖权重越大,说明该项在两者关系中越重要。
两个测试项之间边的权值计算公式如下:
(1)
式中:0≤Wij≤1,0≤dc≤1,0≤dd≤1,0≤di≤1,0≤dp≤1,0≤dt≤1,0≤do≤1。
2.2 基于三元闭包理论计算测试项相关概率
2.2.1 计算邻里重叠度
邻里重叠度用Oij来表示。用N(i)和N(j)分别表示第i个测试项和第j个测试项,通过定义(i,j)边的“与N(i)、N(j)均为邻居的节点数即|N(i)∩N(j)|”与“N(i)、N(j)边中至少一个为邻居的节点数即|N(i)∪N(j)|”的比值来表示Oij,公式如下:
(2)
Step1 获取所有测试项。
Step2 找出所有入度和出度都大于零的测试项,即交点。
Step3 获取第一层次的三元关系组。如果交点的入度是未通过测试项,假设未通过数量为m,遍历交点所有出度,假设出度为n,则保存所有包含任一入度未通过测试项,交点测试项,任一交点出度为一个三元关系组,共有n×m个三元关系组。
Step4 获取下一层次的三元关系组。对于上一层次的每一个三元关系组,判断出度测试项的出度是否大于0,如果大于0,假设第x层次的出度数量为k(x),以上一层次的三元关系组中交点作为三元关系组的入度点,上一层次的三元关系组中的出度作为交点,任一出度测试项的出度为三元关系组,即共有k(x)个三元关系组。
Step5 重复Step 4直到k(x)数量为0,即共有n×m×k(1)×k(2)×…×k(x)个三元关系组。
Step6 获得了所有的三元关系组之后,计算三元关系组的入度测试项N(i)和出度测试项N(j)的交点数|N(i)∩N(j)|,还有并集数|N(i)∪N(j)|。
Step7 得出N(i)和N(j)的邻里重叠度值。
2.2.2 计算测试项i的聚集系数Ci
节点A的聚集系数,即A的任意两个朋友也是朋友的概率。
Step1 获取所有测试项。
Step2 计算测试项的出度。
Step3 如果出度存在且大于1,存入邻居数组,往下面步骤走;否则Ci为0,程序结束。
Step4 计算邻居总对数:
邻居总对数=(测试项出度/测试项出度 -1)/2。
(3)
Step5 计算邻居间朋友对个数。
Step6 计算聚集系数Ci:

。
(4)
2.3 计算测试项推荐系数
Step1 如果测试项为不通过,推荐系数直接为1。
Step2 如果测试项为通过,推荐系数=所有直接相连的未通过测试项边权重之和+所有相连的第一层三元闭包下的推荐值+所有相连的第二层三元闭包下的推荐值+…+所有相连的第一层三元闭包下的推荐值,若结果大于1,则该测试项的推荐系数等于1。
设测试项N(i)的推荐系数为Ri(0≤Ri≤1),第n层相连三元闭包下的推荐值为Ri(n),N(j)表示直接相连的未通过测试项,Wij表示连接测试项N(i)和测试项N(j)边的权值,第一个求和表达的是和测试项N(i)直接相连的所有未通过测试项的边权值之和,第二个求和表达的是和测试项N(i)相连的所有第一层三元闭包推荐值之和,第三个求和表达的是和测试项N(i)相连的所有第二层三元闭包推荐值,第n-1个求和表达的是和测试项N(i)相连的所有第n层三元闭包推荐值之和,公式如下:
(5)
若测试项N(i)处于第1层相连三元闭包中,第1层相连三元闭包下的推荐值为Ri(1)的计算方法如公式(6)所示。测试项N(i)为三元关系组中的出度点,N(q)为三元关系组中的交点,测试项N(p)为三元关系组中的入度点,且N(p)为未通过测试项。Opi表示测试项N(p)和测试项N(i)的邻里重叠度,Cq表示测试项N(q)的聚集系数,Rp表示测试项N(p)的推荐系数,Rq表示测试项N(q)的推荐系数。
(6)
若测试项N(i)处于第2层相连三元闭包中,第2层相连三元闭包下的推荐值为Ri(2)的计算方法如公式(7)所示。测试项N(k)为三元关系组中的出度点,N(q)为三元关系组中的交点,测试项N(p)为三元关系组中的入度点,且N(p)为未通过测试项,测试项N(i)为测试项N(k)的出度点。Oqi表示测试项N(q)和测试项N(i)的邻里重叠度,Ck表示测试项N(k)的聚集系数,Rq表示测试项N(q)的推荐系数,Rk表示测试项N(k)的推荐系数。
(7)
若测试项N(i)处于第n层相连三元闭包中,第n层相连三元闭包下的推荐值为Ri(n)的计算方法如公式(8)所示。测试项N(k)为三元关系组中的出度点,N(q)为三元关系组中的交点,测试项N(p)为三元关系组中的入度点,且N(p)为未通过测试项,测试项N(a)为测试项N(k)的出度点,测试项N(b)为测试项N(a)的出度点…一直到无出度点的测试项N(i)处为止。设测试项的N(i)前两项分别为测试项N(s)和测试项N(t)。
(8)
式中:Osi表示测试项N(s)和测试项N(i)的邻里重叠度,Ct表示测试项N(t)的聚集系数,Rs表示测试项N(s)的推荐系数,Rt表示测试项N(t)的推荐系数。
3 工程应用实践
在网络频率规划管理软件项目回归测试上应用该算法,共有42个功能项,其中无需进行测试的功能项23个,已通过功能项6个,有缺陷功能项共有13个,如表1所示,其中无需进行测试的功能项不再计入统计范围。

表1 项目首轮测试结果
将项目网络频率规划管理软件所有功能项抽象为虚拟人,通过赋予边关系权值方式为虚拟人之间定义交流通道类型,N(i)和N(j)分别表示第i个测试项和第j个测试项,如表2所示。

表2 虚拟人之间定义交流通道类型
未运行测试项推荐系数为0,未通过测试项推荐系数为1,本算法影响域分析之后,本项目已通过测试项的推荐系数如表3所示。
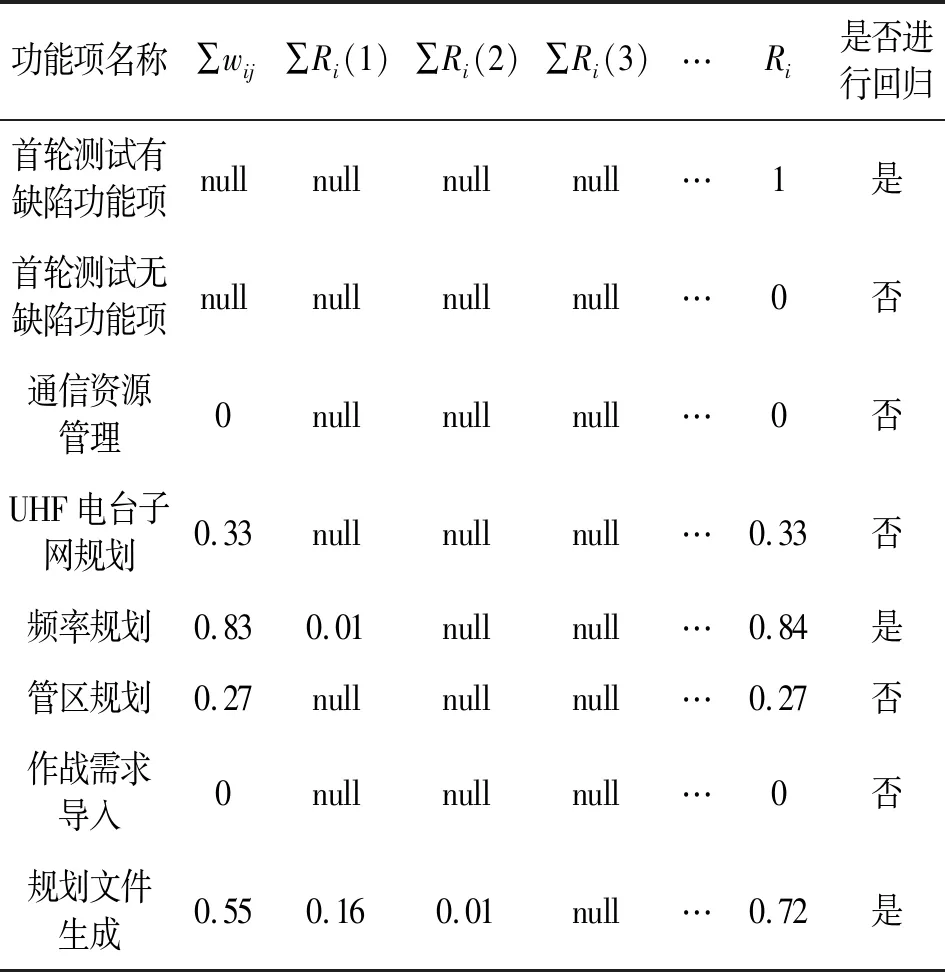
表3 各功能项推荐系数
根据表3结果可知,经过影响域分析算法计算,首轮测试中无缺陷的“频率规划”和“规划文件生成”两个功能项需要进入回归测试。在回归测试中,“频率规划”功能项出现了3个缺陷,“规划文件”功能项回归出现了2个缺陷。下面具体展开“频率规划”功能项缺陷。
(1)由于“VHF电台子网规划”中测试用例“在界面编辑定频频率,包括定频范围内的异常边界值、异常值以及频率间隔异常”中,存在缺陷“范围未判断”,修复此测试用例的缺陷后,影响了“频率规划”功能项的测试用例“通过界面设置VHF电台子网频率规划”,产生了新缺陷“范围并未同步,输入异常数据,软件没有停止处理,没有提示异常”。
(2)在“频率管理”测试用例“选择禁用频率类型为救生频率,输入值为异常值及异常边界值”中,存在缺陷“救生范围未判断”。修复此测试用例的缺陷后,影响了频率规划功能项的测试用例“通过界面设置救生频率”,产生了新缺陷“范围并未同步,输入异常数据,软件没有停止处理,没有提示异常”。
(3)“网络拓扑规划”中某测试用例的步骤之一“规划UHF电台子网”存在“重进之后,拓扑图连线与之前规划不一致”的缺陷,修复之后,导致UHF电台子界面无法显示出网络拓扑图中规划的UHF子网,从而导致“频率规划”中无法通过界面设置UHF电台子网频率规划。
由项目实践结果可知,该算法在以下两种情况中表现优异:一是将所有测试项进行回归测试的案例——共19个测试项,案例情况下,需要回归19个测试项,101个测试用例,使用本算法只需回归15个测试项,74个测试用例,实现了测试用例集约简,测试效率得到了较大提升;二是只对有缺陷的测试项进行回归测试的案例——共19个测试项,案例情况下,需要回归13个有缺陷的测试项,66个测试用例,使用本算法在回归所有有缺陷测试用例的情况下,计算由于程序变更或其他依赖关系所可能导致其他测试用例出现缺陷的概率,得出额外有2个测试项,8个测试用例可能出现缺陷,测试充分性和覆盖率得到了较大提升。
4 实验结果与分析
本节将列举本文算法在网络频率规划管理软件、任务数据接入处理软件、侦察过程回放软件、导调控制检测软件和海事五代星实装训练软件这五个软件回归测试中的表现。如表4所示,“测试用例数”等于轮次测试下“已通过测试用例数”和“有缺陷的测试用例数”之和,不包含轮次下未执行测试用例数。

表4 算法在五个软件回归测试的表现
由表4的实验结果可知,该算法在五个项目应用中将五个软件系统抽象为五个社交网络,软件系统提供的功能抽象为虚拟人,为虚拟人之间定义交流通道类型,通过图论和三元闭包理论构建非直接发生联系的人的关系,给出回归建议。与将所有测试项进行回归测试的案例相比,实际回归测试用例数远少于所有测试用例数,实现了测试用例集的约简;与只对有缺陷的测试项进行回归测试的案例相比,实际回归测试用例数大于轮次测试下有缺陷的测试用例数,预测了由于测试项更改引发其他测试项出现新缺陷的概率,从而决定是否将其他测试项进行回归测试。工程应用实践结果表明,本文算法在回归测试中有可能发现新缺陷,可以在一定程度上提升回归测试的充分性和覆盖率。
5 结束语
本文应用三元闭包理论梳理测试项关系,结合图论建立测试项社区网络,寻找定位可能受到影响的测试项,实现测试用例约简的同时,将可能有缺陷概率的测试项纳入回归测试,可能发现新缺陷,节约了人力成本,减少了资源的消耗,具有较大的实用价值。但本文在测试项与测试项之间的权值取值上没有具体到代码层面,这也是后续改进的方向。
